On the Buckling Response of Offshore Pipelines under Combined Tension,Bending,and External Pressure
Yanbin Wang,Deli Gao,Jun Fang
On the Buckling Response of Offshore Pipelines under Combined Tension,Bending,and External Pressure
Yanbin Wang1,2,Deli Gao1,Jun Fang1
In this paper,the buckling and collapse analysis of offshore pipeline under combined tension,bending moment,and external pressure has been presented with theoretical analysis and FE(finite element)simulation method respectively.Based on the model initially proposed by Kyriakides,a 2-D theoretical model has been further developed.To verify the correctness and accuracy of the model proposed in this paper,numerical simulations have been conducted with 3-D FE model using ABAQUS software.Good consistency has been shown between the calculation results which validate the availability of the theoretical analysis.On this basis,the influence of load path,material properties,and diameter-to-thickness ratio on the buckling behaviors of the pipes have been discussed.Based upon the discussion mentioned above,some significant conclusions have been drawn.
Offshore pipelines;Bucking analysis;Combined loads;Theoretical model;FE simulation
1 Introduction
Submarine pipelines are important parts in offshore oil and gas drilling and exploitation.Severe loads will be induced during the installation of pipelines,which will result in unpredictable risks and challenges.Combined tension,bending,and external pressure will cause to happen during installation regardless of the installation method[Kashani and Young(2005);Li,Wang,He,and Zhao(2008)].Under the loads mentioned above,pipelines are vulnerable to ovalization in the cross section.Localized deformation caused by pipe-laying operation or initial imperfection can lead to local buckling,which will,in turn,have the potential of initiating a propagating buckle,and then the buckling rapidly advances in the longitudinal direction,resulting the failure of pipelines and causing huge economic loss.
Due to the importance of the buckling response of the pipes,great efforts have been devoted to this topic in the past few decades.Gellin(1980)has addressed the effect of nonlinear material behavior on the bucking behavior of a cylindrical shell under pure bending.Kyriakides and Shaw(1982)have analyzed the response and stability of elastoplastic circular pipes under combined bending and external pressure,and have figured out the maximum moment and curvature as a function of the material and geometric parameters for different pressures.Subsequently,the stability of tubes under combined bending and external pressure has been studied by Corona and Kyriakides(1988)who have found that the buckling response of pipes,critical collapse loads,and the characteristics of instabilities have been strongly affected by the loading path in their research(bending followed by pressure and pressure followed by bending).Besides,Kyriakides,and Shaw(1985)have conducted the inelastic analysis of circular tubes under cyclic bending,in which several nonlinear hardening plasticity models have been adopted to predict the growth of the ovalization.Dyau and Kyriakides(1992)have developed a 2-D model to study the buckling response of tubes under combined bending and tension.A deterministic model have been proposed by Al-Sharif and Preston(1996)to calculate the collapse of the pipes under combined bending and pressure,and a numerical model has been developed to verify the effective of the theoretical analysis.Moreover,Kyriakides and Corona(2007)have given some analysis on the collapse of thickwalled pipes under different load combinations,i.e.,pressure and bending,presure and tension,and tension and bending.Numerical studies on the behavior of thick-walled tubes with simultaneous tension,bending,and external pressure have been performed by Bai,Igland,and Moan(1997)using ABAQUS.Recently,the buckling characteristics of offshore pipes under pure bending,and combined bending and external pressure have been investigated by Yuan,Gong,Jin,and Zhao(2009),who have indicated the buckling performance of the pipes is closely related with the diameter-to-thickness ratio and the initial curvature.
This paper aims to present a further investigation on the buckling performance of thick-walled tubes under combined tension,bending,and external pressure based on the general theory proposed by Kyriakides and his co-workers.We assume that the buckling behavior is symmetric about the neutral plane and the deformation is uniform along the axis of the tube.The strain-displacement relationship is obtained according to the nonlinear ring theory,and then a set of equilibrium equations is formulated based on virtual work approach.Meanwhile,a 3-D numerical model is developed to compare the results between the two methods.Furthermore,the buckling responses under different load paths have been studied,and corresponding parametric study concerning several important influence factors have been conducted.At last,some significant conclusions have been drawn in the end of the paper.
2 Theoretical formulations
2.1 Kinematics
The geometric parameters and coordinate system is presented in Figure 1.As shown in Figure 1,the coordinatezis the radial distance from the mid-surface of the tube wall,and the axial,circumferential and radial coordinates are denoted asx,θ andz.The displacements of a point on the mid-surface areu,vandwwith respect tox,θ andzrespectively.Uniform tensionT,bending momentM,curvature κ and external pressurePare assumed to be applied along the length of the tube.In order for convenient calculation and formula derivation,the following assumptions are used to stipulate the present formulation[Gellin(1980)]:
·The plane sections are normal to the mid-surface of the tube cross-section before and during deformation.
·Small strain and finite rotations about the axes are accepted.
·The pipe is a circular and thick-walled tube with mean radiusRand thicknesst.
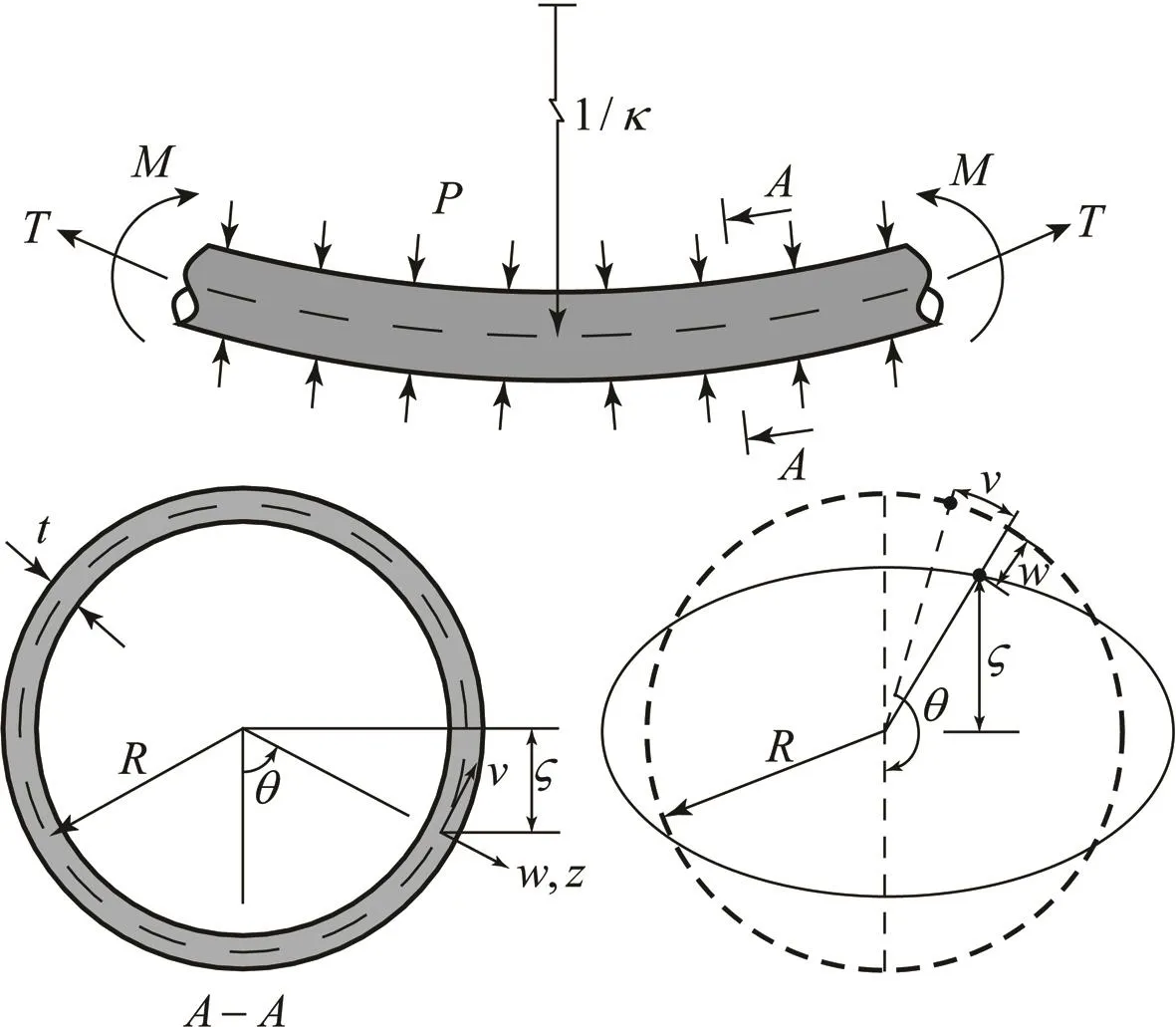
Figure 1:Geometric parameters and coordinate system ς is the distance from the neutral axis to the tube wall.
The circumferential tension strain can be denoted as:

Whereeand β are defined by:

and

A finite rotation φ about the axis is defined as:

Thus,the circumferential curvature can be expressed as:

The circumferential strain of the deformed cross section can be denoted as:

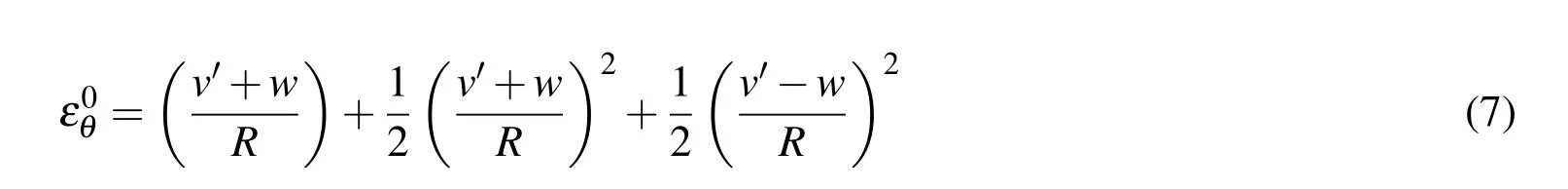
and
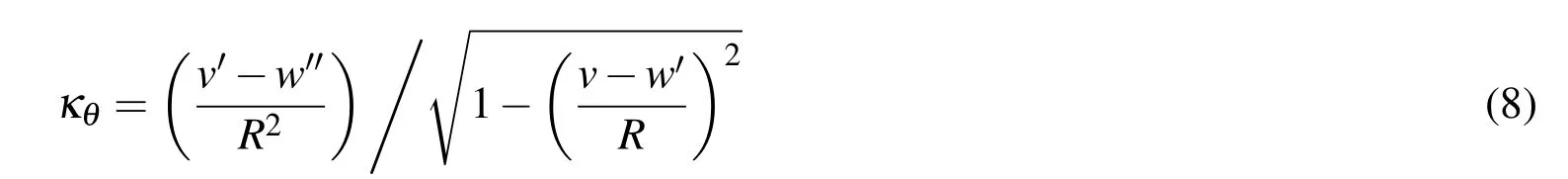
Where(′)denotes the differentiation with respect to θ.
The axial strain can be described as:

1,which is:

2.2 Constitutive model
Due to the good plastic deformation performance of deep water pipelines,the tube can be modeled as an elastoplastic material.In this paper,the Ramberg-Osgood model,as shown in Figure 2,is used to describe the nonlinear stress-strain relationships of the material,which is given by:

WhereEis Young’s modulus,σyis the effective yield stress andnis the hardening parameter of the material.
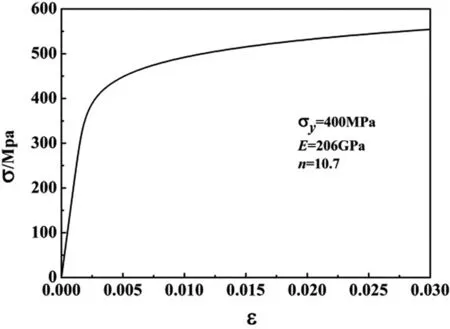
Figure 2:Stress-strain relationship for the Ramberg-Osgood constitutive model.
In this paper,the incrementalJ2plastic f l ow theory with isotropic hardening is adopted to model the plastic behavior of material.The components of radial stress(σr)and shear stress(σrx,σrθ,σθx)are disregarded due to the fact that these components are quite small as compared with the axial stress and the circumferential stress.Therefore,the incremental constitutive model can be simplified as follows:
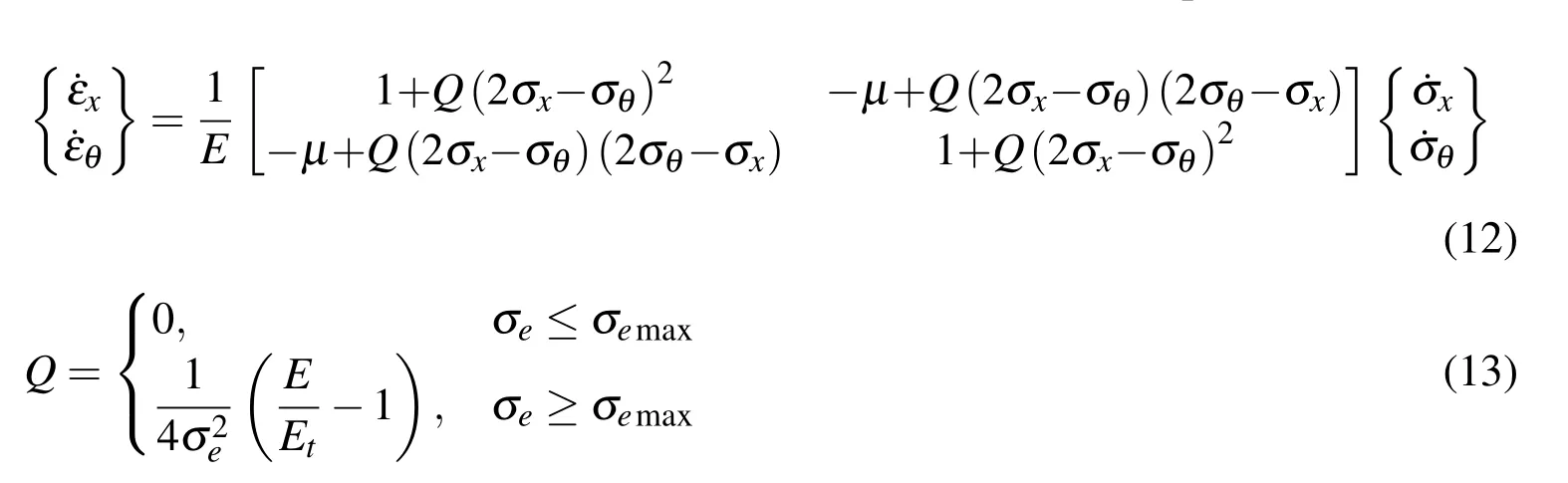
Where σeis the equivalent stress andEt=Et(σe)is the tangent modulus of the material.They are given as follows:

WhereSijis the deviatoric stress tensor,σijis the stress tensor,σkkis the first invariant stress tensor,and δijis the Kronecker Delta function.
2.3 Principle of Virtual Work
According to the principle of virtual work,the equation below must be satisfied when the tube is in an equilibrium state,which is:

Where δWis the virtual work of the external loads,andVis the volume of the material of the tube.For the case of incremental loads,the equation becomes:
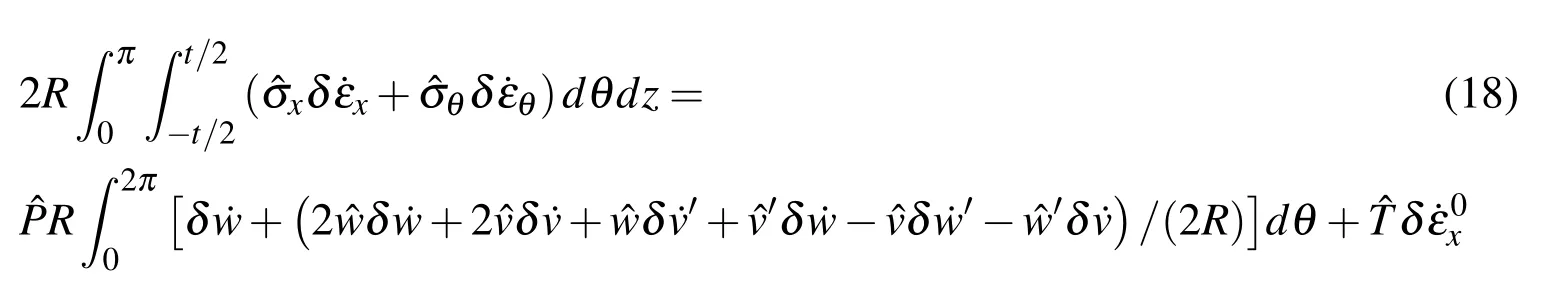
On the left side of Eq.18 is the increment of virtual work done by the internal stress,whereas the right side is the increment of virtual work done by the external pressure.When it comes to the problem of pure bending,external work on the right side equals zero because of the prescribed curvature.σijand εijrepresent the stress strain component respectively.(·)denotes an increment in(),while(∧)denotes for the next equilibrium state.
The left side of Eq.18 can be expressed as:

From Eq.6,Eq.9 and Eq.10,the following equations can be obtained:
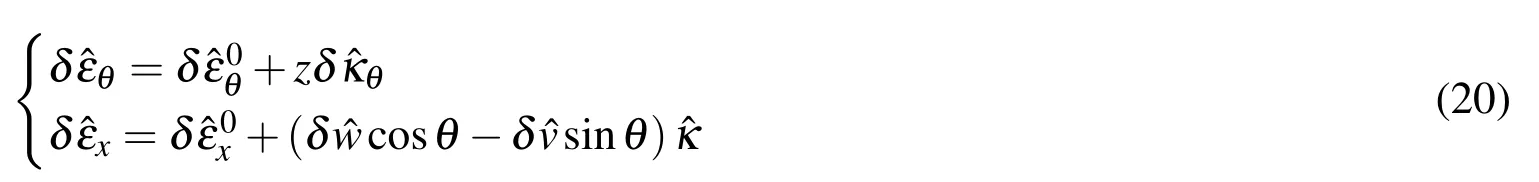
Where,
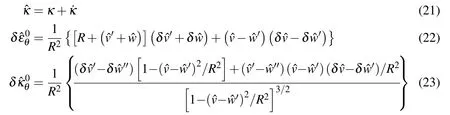
It is assumed that the deformations of the cross section,i.e.,the in-plane displacementwandv,are symmetric about the axis θ=0,and they are the functions of θ.Therefore,wandvcan be approximated by the following expressions[Gellin(1980)].
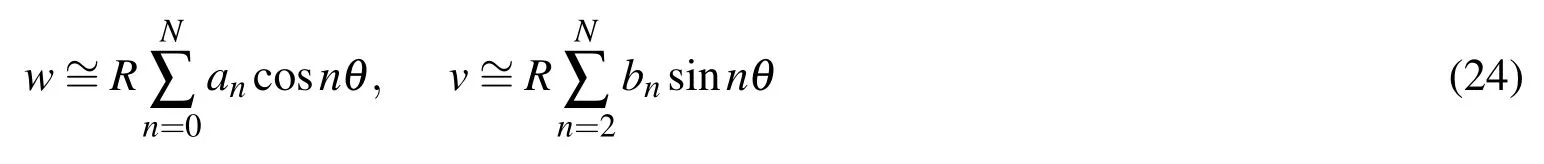
Substituting Eq.24 into Eq.20∼Eq.23 and then substituting the results into Eq.18,since Eq.18 is an identical equation for arbitrary δˆan,δˆbnand δˆε0x,the following nonlinear algebraic equations can be obtained:
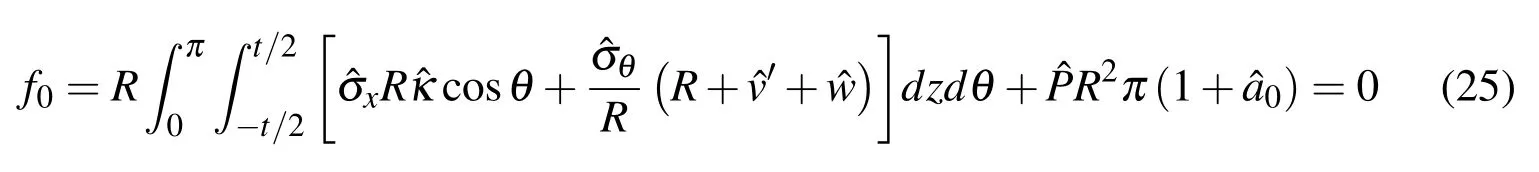
When 1≤n≤N,
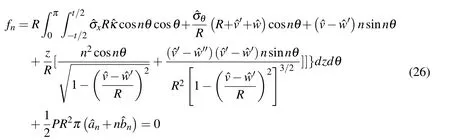
WhenN+1≤n≤2N-1,


A set of 2N+1 nonlinear algebraic equations is determined by Eq.25∼Eq.28.The solution of the equations is obtained by Newton-Raphson method.The iteration scheme encompasses nested iterations for the constitutive relations,which is provided by Shaw and Kyriakides(1985)in detail.
2.4 Numerical solution
A set of 2N+1 nonlinear algebraic equations is included in the present solution.Some parameters should be prescribed,namely geometric dimensions,material parameters,as well as initial imperfections and initial stress of tube.In the numerical calculation,the numbers of integration points,for the half cross section of the tube,along the circumferential direction and through the thickness arekandl,respectively.In the case of pure bending,the calculation procedure is controlled by curvature κ.By the specification of the curvature incrementˆκ,the converged solution of the previous step is regarded as the initial estimate of the nodal displacements for the next step.Subsequently,strain increment can be obtained through nodal displacements and curvature,and then the stress increment can be achieved according to the constitutive model.After obtaining the stress components of each integration points,Eq.25∼Eq.28 can be solved by the Newton-Raphson method.Strains,stresses as well displacements are updated when the converged solution is achieved.It is found that the solution can meet the precision requirements whenNranges from 4 to 6.In the case of pure bending,k=12 andl=5 are appropriate.While for the combined case,the mesh should be finer,therefore,integration points through the thickness,i.e.l=7 would be more reasonable.
In the case of the combined loads,the calculation procedure is controlled by prescribing curvatureˆκ as well pressure incrementˆPor the increment of the displace-ment coefficienta2(mainly concerned with the ovality).The control of displacement is required to identify the limit pressure more accurately.As to the value of the parameters,the pressure incrementˆPshould not exceed 0.1 MPa,and the ellipticity increment(ΔD/D)should not exceed 0.01%.
After the solution of each load increment being calculated,the moment can be expressed as follows:

The main steps of solution procedure for the combined loading case are shown in the f l ow chart in Figure 3.If the prescribedPin the f l ow chart equals zero,it would be reduce to the pure bending case.
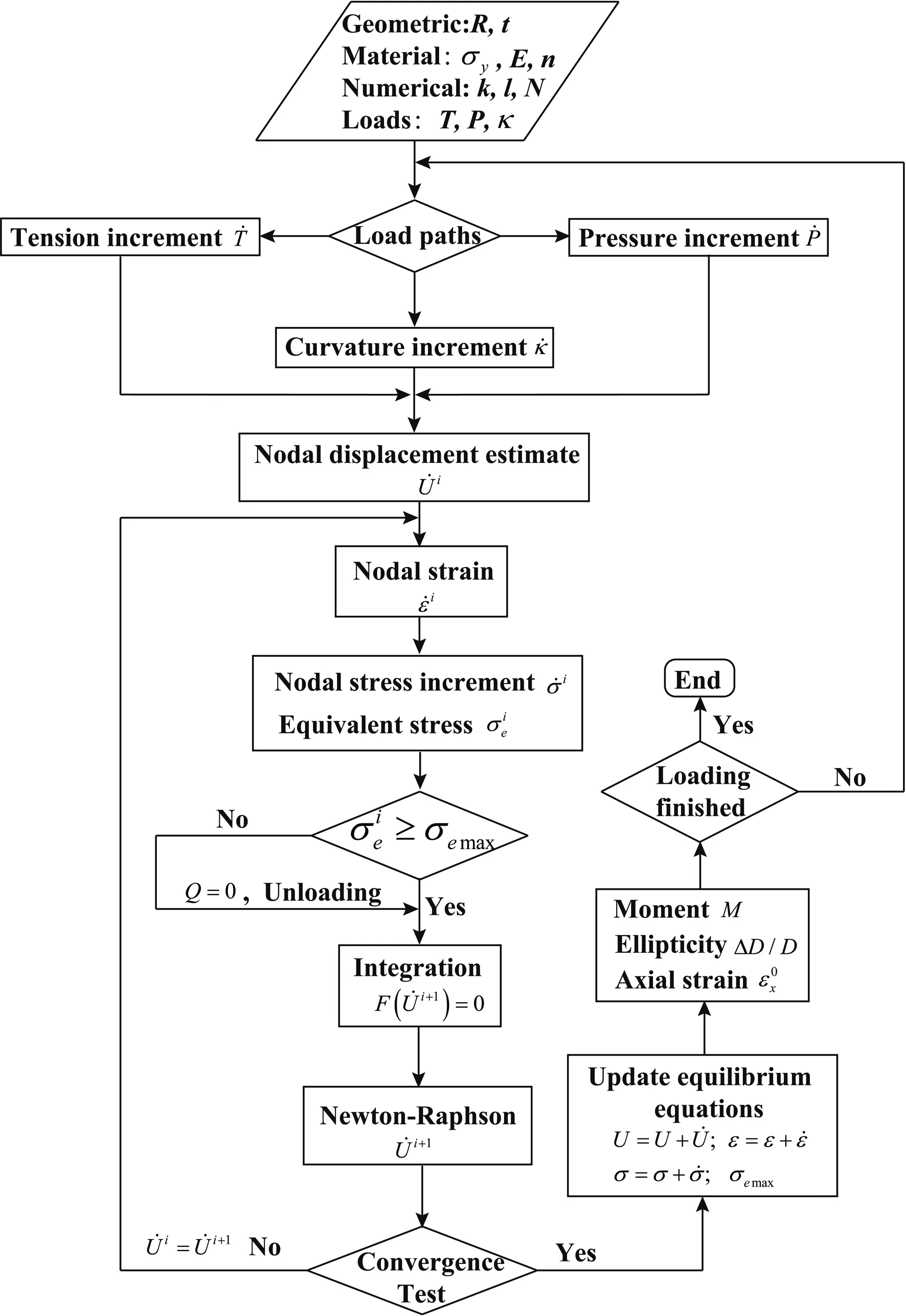
Figure 3:Flow chart of numerical solution procedure.
3 Numerical simulations
A finite element model is developed within the framework of the software ABAQUS to simulate the buckling behavior of pipes under simultaneous tension,bending,and external pressure.3D,eight-node incompatible solid element,C3D8I,is chosen to model the pipe.Since this type of element is enhanced by incompatible modes to bending behavior,it is best suited for the present problem[Simo and Armero(1992);Hibbitt,Karlsson,and Sorensen 2006].TheJ2f l ow theory of plasticity with isotropic hardening proposed by Cotuna,Lee,and Kyriakides(2006)is adopted to describe the plastic behavior of material,and the Ramberg-Osgood constitutive model is used by multi-linear approximations of the stress-strain curve shown in Figure 2.
The symmetry of the loads and deformations reduces the problem to a quarter of a pipe.As a result,symmetrical boundary conditions are applied at the mid-span(X=0)andZ=0 planes(Figure 4).Besides,additional spring constraints along vertical direction(Y)are applied at the mid-span plane.This kind of elastic constraints is desirable for this problem since it can avoid the stress concentration phenomenon which is inevitable if rigid constraints are applied.

Figure 4:Finite element mesh and loadings.
Kinematic coupling relationship is imposed between the nodes on the right end of the tube and a reference point(the central node or the bottom one are both suitable).The right end plane is constrained to remain plane in the loading process,and at the same time the cross-section should be free to deform.The curvature is applied by prescribing the angle of rotation at the reference point,φ,Likewise,uniform tension is applied to the model through this reference point,and hydrostatic pressure is implemented on the external surface of the pipe.Thus,the average curvature of the section can be given by:

To facilitate the development of buckling deformation,the length of the pipe,L=3Dis considered to be suitable.The pipe model is meshed into 6 parts through the thickness,100 parts around the half circumference and 100 parts along the length,which is found to be adequate.Figure 4 illustrates a typical finite element mesh used in the analyses.Furthermore,the Nlgeom option is selected for the nonlinear calculation,and the Riks algorithm(arch length method)is adopted here.
4 Results and discussion
4.1 Illustrative example using theoretical formulations
The maximum curvature in the sag-bend region of marine pipelines often occurs close to the seabed where the maximum water depth is reached.Considering that the curvature and hydrostatic pressure exerted on the pipes increases with the depth of the water,while axial tension is nearly maintained constant,the case ofT→Radial(κ,P)loading path is examined.
The pipe is first tensioned incrementally to a chosen valueT=1000 KN,and then curvature and external pressure are increased proportionately until the values of κ=0.15 andP=10 MPa are reached.The main features of the pipe response subjected to the combined loads are illustrated in Figure 5 for a pipe with its diameterD=254 mm(10 inch)andD/t=20.The predicted ellipticity-water depth,ellipticity curvature,axial strain-curvature,and moment-curvature curves are shown in this figure.The increase of ellipticity is approximately proportional to the curvature and water depth at the beginning.However,the nonlinearity becomes more and more notable as the loads augment.As to the axial strain of the pipe,it nearly experiences a linear growth with curvature.In addition,it can be seen from moment-curvature response that there exhibits a limit moment before collapse.Once attaining the limit moment,localized deformation would quickly develop in a region of about 5 to 6 times of the tube diameters,which can be taken as the critical state of buckling.
4.2 Comparisons of finite element analysis results with theoretical solutions
Numerical simulations and theoretical calculations are carried out respectively for the scenario of Radial(T,P,κ)loading path.In other words,three loading parameters{ΔT,ΔP,Δκ}are simultaneously applied to the model.The analyses are performed for the pipe model based on the parameters ofD=254 mm,D/t=20,σy=400 MPa,T=600 kN,P=35 MPa and κ =0.013.The sequences of deformed configuration and stress distribution during the loading process are depicted in Figure 6.
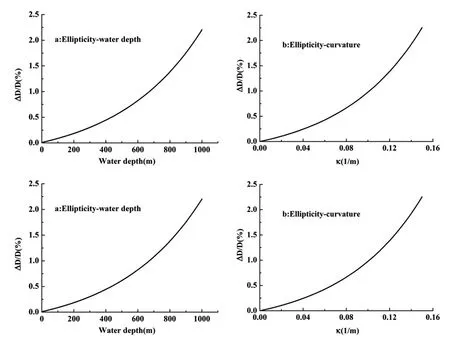
Figure 5:Predicted responses for T → Radial(κ,P)loading path.σy=400 MPa,D/t=20,n=10.7.
The comparison of responses calculated by the two methods is shown in Figure 7.The predicted ellipticity of two models is quite close in the elastic range.However,the increase of theoretical result slightly lags behind that of finite element simulation at high values of loadings.
The main reason for the difference is that ABAQUS uses a finite deformationJ2fl ow theory of plasticity whereas the theoretical formulation in Eqs.(12)∼(16)is small deformation.In addition,the theoretical model simplifies this 3D problem to a 2D one,which only takes into account the stresses along the axial and circumferential directions.The disregard of the secondary radial stress and shear stress will not generate much error in the elastic range.However,with the increase of stress in the radial direction,the discrepancies become more and more notable.Moreover,due to the disregard of radial stress and shear stress,the equivalent stress will be smaller compared with the practical situation,hence,later occurrence of plastic plateau.Likewise,the growth of ellipticity is somewhat delayed.The suitability of the theoretical method used in predicting the buckling response of deepwater pipes has been validated herein.
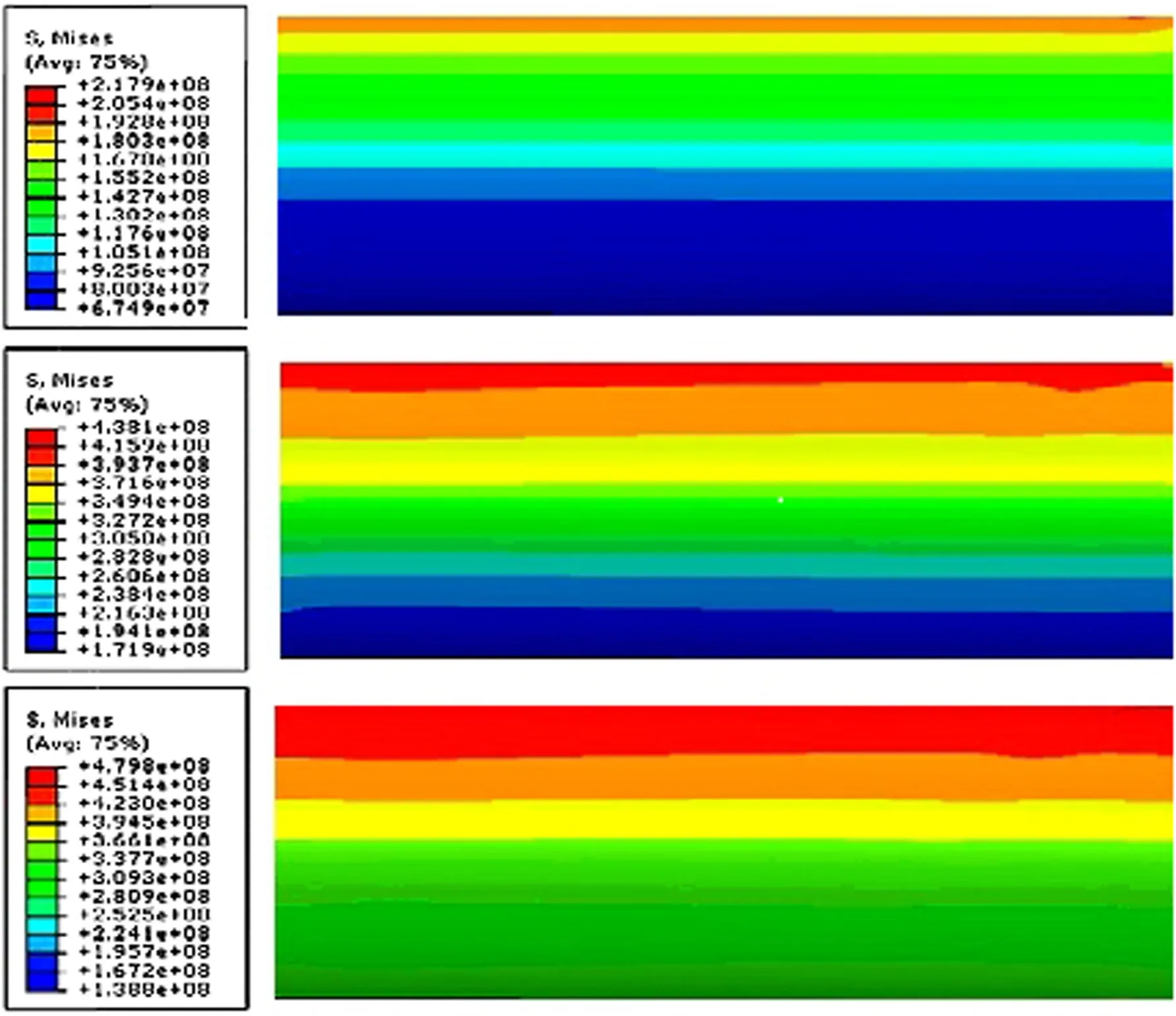
Figure 6:Deformed configuration and stress Distribution during loading process.
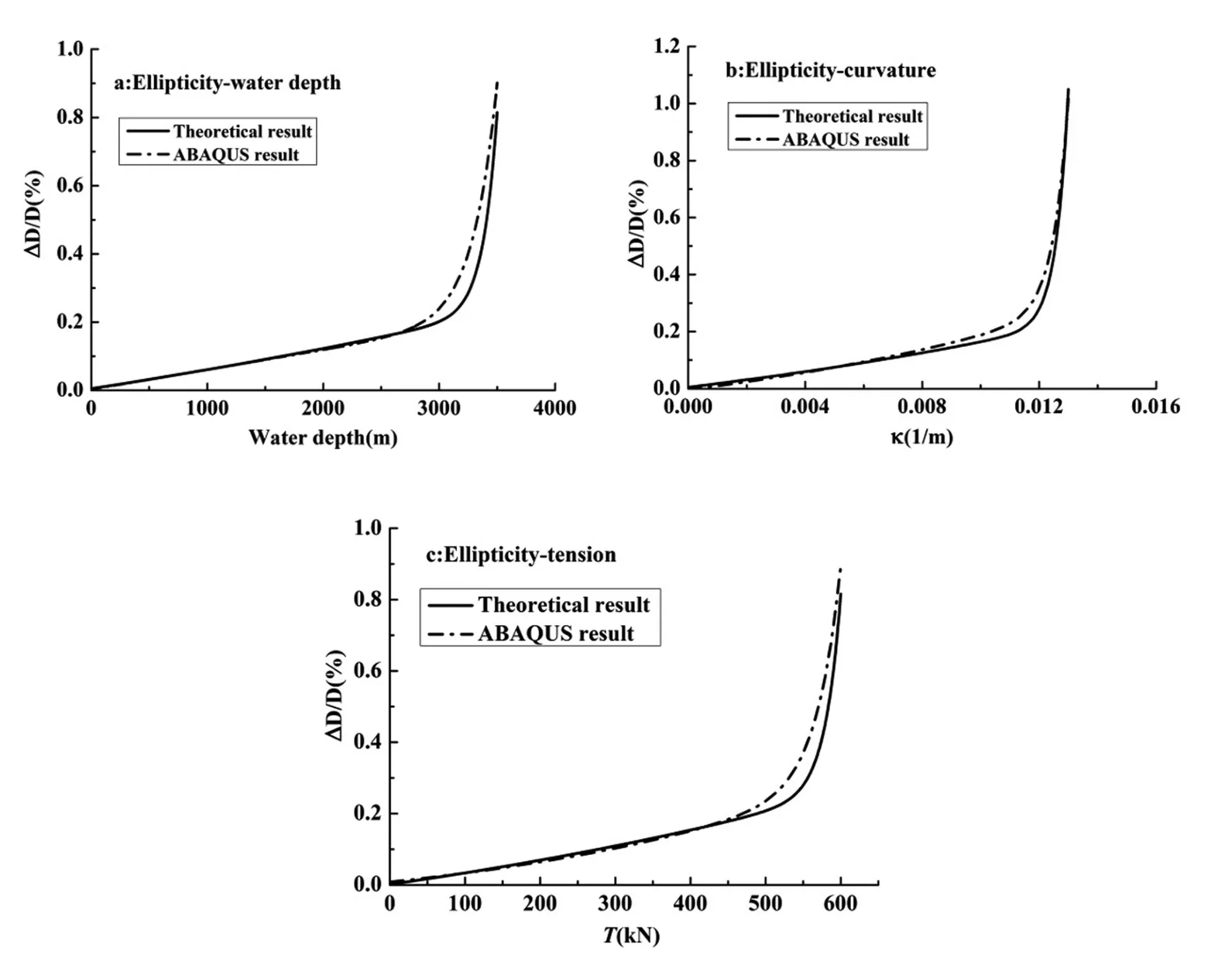
Figure 7:Comparisons of finite element analysis results with theoretical solutions.
4.3 Parametric study
The theoretical model is adopted to examine the effects of several important factors including tensionT,strain-hardening parametern,yield stress σyas well as diameter-to-thickness ratioD/t.T→Radial(κ,P)is the loading path considered in the present section.Besides,some discussions and comparisons are made concerning the design of pipes in engineering practice.
The buckling of tube is related to several factors,such as the diameterD,wall thicknesst,material properties,initial ellipticity ΔD/D,and load history.In addition,residual stress induced in the manufacturing process as well as yield anisotropyplay an important role in the occurrence of tube buckling. For offshore applications,aD/tvalue ranging from 10 to 70 is recommended.While for deep water application,aD/tvalue ranging from 10 to 35 is more suitable.In addition,the yield strength of steel for typical offshore pipelines is commonly between 276 MPa and 448 MPa.Besides,the tubes,with initial ellipticity exceeding 0.5%,should be avoided in the deep water applications[Ju and Kyriakides(1991)].

Figure 8:Limit moment versus applied tension.
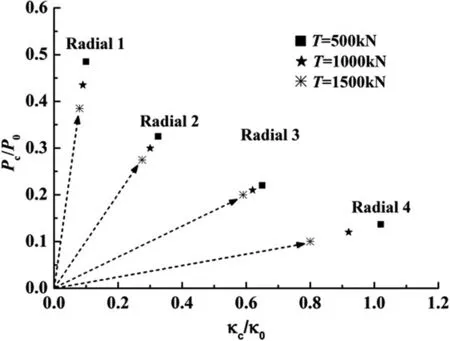
Figure 9:Effects of tension on critical pressure and curvature.
Figure 8 and Figure 9 show that axial tension has a significant effect on bending moment carrying capacity of a pipe.The tension is prescribed to 500 kN,1000 kN,1500kN respectively,and the ratio of(P/P0):(κ/κ0)ranges from5:1,1:1,1:3to 1:8,respectively denoted as Radial 1-Radial 4,which consists of 12 different load combinations.The result indicates that the presence of tension impairs bending moment carrying capacity greatly.With the increase of tension applied,the limit momentMcdrops.Furthermore,it can also be observed that the increase of external pressure will cause the value of limit moment to decrease.Additionally,as can be seen in Fig.9,the predicted critical pressurePcand critical curvature κcbecome smaller when the value of tension increases.It is important to note that the results are normalized to dimensionless factors by the following variables:
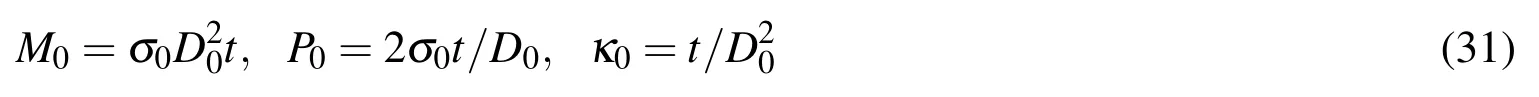
Where mean diameterD0=D-t,and σ0is API yield stress[API(2004)],i.e.,the stress at a strain of 0.005.
Figure 10 shows how the critical pressure and critical curvature vary with the material yield stress σywith other parameters kept constant.Clearly,the tubes with larger yield stress possess higher critical pressure and curvature.In addition,it is also worth noting that at higher curvatures the effect of yield stress is less pronounced compared with the cases of lower curvatures.
Larger strain-hardening parameternmeans larger strain-hardening effect.Figure 11 presents the variation of critical pressure and critical curvature with the strain-hardening parametern.It can be observed that tubes with larger n can sustain larger critical pressure and curvature,i.e.,higher load-carrying capacity.

Figure10:Effects of yield stress on critical pressure and curvature.
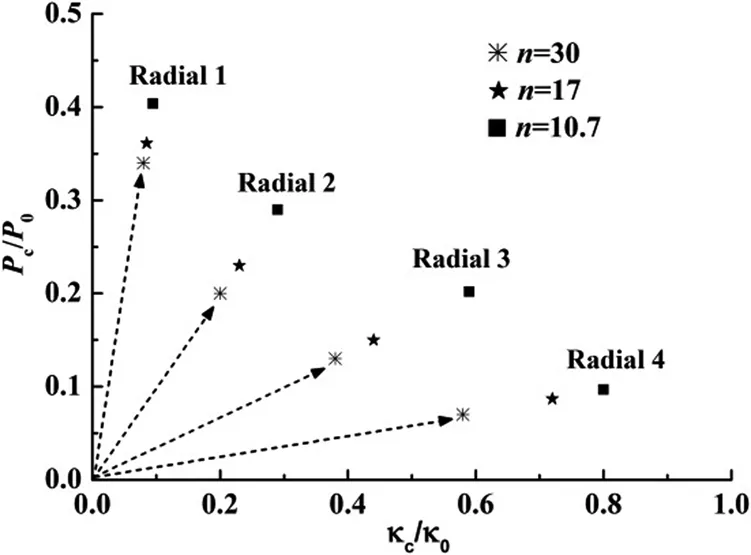
Figure 11:Effects of strain-hardening parameter on critical pressure and curvature.
The effect of diameter-to-thickness ratioD/ton the critical pressure and curvature is examined in Figure 12.ThreeD/tvalues 15,20 and 25 are adopted,while keeping other parameters constant.Just as expected,the limit values corresponding to lowerD/ttubes are higher than those of largerD/tones.In addition,note that the degree of its influence varies with different combinations of loads applied.
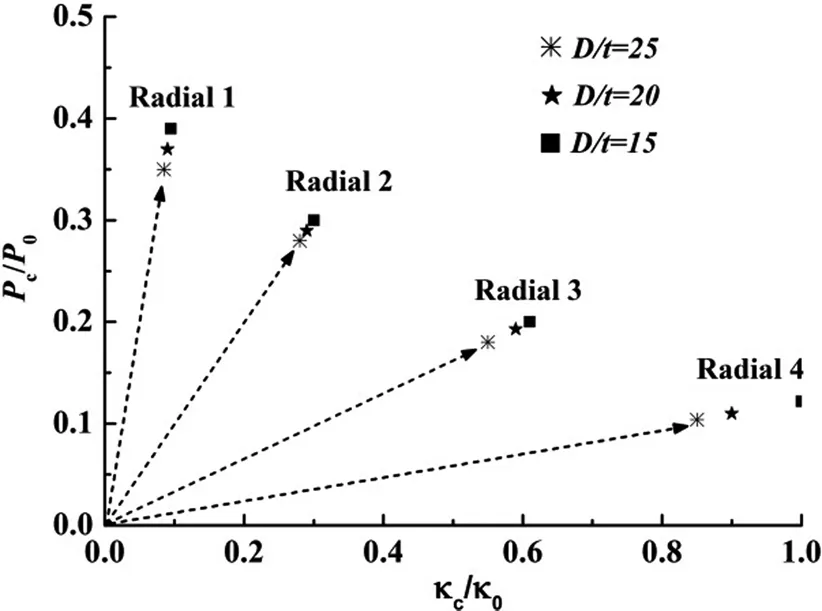
Figure 12:Effects of D/t on critical pressure and curvature.
5 Conclusions
1.The load-carrying capacity of the tube is significantly affected by the tension applied.With the increase of tension,the limit moment obviously drops,and the predicted critical pressure and curvature would become smaller.In the case of equal proportional loading between external pressure and curvature,the effect of tension on load-carrying capacity of the tube is less conspicuous compared with other loading ratio.
2.The buckling behavior and load-carrying capacity of pipes is quite sensitive to material properties.Larger yield stress σyand strain-hardening parameternalways lead to higher limit pressure and curvature,i.e.,stronger resistance to pipe buckling.The critical pressure of the pipe is more susceptible to yield stress rather than strain-hardening parameter,whereas the critical curvature is just the contrary.Therefore,the high strength steel is preferred to improve the resistance to external pressure for deepwater pipes in the practical engineering.
3.Diameter-to-thickness ratioD/tplays a very important role in buckling response of pipes.In general,pipes with lowerD/tvalues possess stronger capability to resist the buckling deformation.But,the degree of its influence varies with different combination of loads applied.In summary,it can be concluded that the theoretical formulation and solution method described in this context could provide a reasonably-accurate estimate of the buckling and collapse of deep water pipes.In addition,it should be mentioned that experiments under simultaneous tension,bending,and external pressure should be carried out,and thus,effectiveness of this theoretical method can be carefully examined.
Acknowledgement:The authors gratefully acknowledge the financial support from the Natural Science Foundation of China(NSFC,51521063,U1262201).
Al-Sharif,A.M.;Preston,R.(1996):Simulation of Thick-Walled Submarine Pipeline Collapse under Bending and Hydrostatic Pressure.Proceedings of Offshore Technology Conferences,Houston,Texas,USA,OTC8212,pp.589-598.
American Petroleum Insitute.(2004):API specifications SL:specifications for Line Pipe(43rd Ed)API Publishing Services,Washington DC,USA
Bai,Y.;Igland,R.T.;Moan,T.(1997):Tube collapse under combined external pressure,tension and bending.Marine Structures,vol.10,no.5,pp.89-410.
Corona,E.;Kyriakides,S.(1988):On the collapse of inelastic tubes under combined bending and pressure.International Journal of Solids and Structures,vol.24,no.5,pp.505-535.
Corona,E.;Lee,L.H.;Kyriakides,S.(2006):Yield anisotropy effects on buckling of circular tubes under bending.International Journal of Solids and Structures,vol.43,no.22,pp.7099-7118.
Dyau,J.Y.;Kyriakides,S.(1992):On the response of elastic plastic tubes under combined bending and tension.Journal of Offshore Mechanics and Arctic Engineering,vol.114,no.1,pp.50-62.
Gellin,S.(1980):Plastic buckling of long cylindrical shells under pure bending.International Journal of Solids and Structures,vol.16,no.5,pp.397-407.
Hibbitt,H.D.;Karlsson,B.I.;Sorensen,P.(2006):ABAQUS Theory Manual,Version 6.3.Pawtucket,Rhode Island,USA.
Ju,G.T.;Kyriakides,S.(1991):Bifurcation buckling versus limit load instabilities of elastic-plastic tubes under bending and external pressure.Journal of Offshore Mechanics and Arctic Engineering,vol.113,no.1,pp.43-52.
Kashani,M.;Young,R.(2005):Installation load consideration in ultra-deepwater pipeline sizing.ASCE Journal of Transportation Engineering,vol.131,no.8,pp.632-639.
Kyriakides,S.;Corona,E.(2007):Mechanics of Offshore Pipelines,Volume 1:Buckling and Collapse.Elsevier Science,Oxford,UK and Burlington,Massachusetts.
Kyriakides,S.;Shaw,P.K.(1982):Response and stability of elastoplastic circular pipes under combined bending and external pressure.International Journal of Solids and Structures,vol.18.no.11,pp.957-973.
Li,Z.G.;Wang,C.;He,N.;Zhao,D.Y.(2008):An overview of deepwater pipeline laying technology.China Ocean Engineering,vol.22,no.3,pp.521-532.
Shaw,P.K.;Kyriakides,S.(1985):Inelastic analysis of thin-walled tubes under cyclic bending.International Journal of Solids and Structures,vol.21,no.11,pp.1073-1110.
Simo,J.C.;Armero,F.(1992):Geometrically non-linear enhanced strain mixed methods and the method of income-partible modes.International Journal for Numerical Methods in Engineering,vol.33,no.7,pp.1413-1449.
Yuan,L.;Gong,S.F.;Jin,W.L.L,Z.G.;Zhao,D.Y.(2009):Analysis on buckling performance of submarine pipelines during deepwater pipe-laying operation.China Ocean Engineering,vol.23,no.2,pp.303-316.
1MOE Key Laboratory of Petroleum Engineering,China University of Petroleum,Beijing102249,China
2First and corresponding author:Yanbin Wang,Tel:+86 10 89733702,E-mail:wyb76219861@126.com
 Computers Materials&Continua2015年10期
Computers Materials&Continua2015年10期
- Computers Materials&Continua的其它文章
- Minimizing Thermal Residual Stress in Ni/Al2O3 Functionally Graded Material Plate by Volume Fraction Optimization
- Development and Optimization of an Unstructured Kinetic Model for Sodium Gluconate Fermentation Process
- Study on Lateral Nonlinear Dynamic Response of Deep water Drilling Riser with Consideration of The Vessel Motions in Its Installation
