高分辨率遥感影像下线特征提取方法比较
杨志刚,张世奇
(1.广东省国土资源测绘院,广东广州510500;2.中国地图出版社,北京100054)
一、引 言
在摄影测量与遥感、模式识别、计算机视觉及数字图像处理等领域中,线特征提取是一个十分基础和重要的环节[1]。对于一幅高分辨率遥感影像,如何选择最合适的线特征提取算法具有重要的意义。
本文以高分辨率遥感影像为数据源,通过对几种具有代表性的线特征提取算法的试验,分析各种算法的参数自适性,并且从自适性、速度、稳定性、可靠性、自动化程度等5个方面对各种算法的特性、适用场合等进行分析和比较,为对影像的进一步分析及影像匹配打下基础。
二、线特征提取算子原理
1.Hough变换
Hough变换是一种基于变换域的直线提取方法,它从直线的特性出发,考虑能唯一确定直线的两个参数ρ、θ,将直线变换到参数空间中,通过检测参数空间中的极值点来确定直线的参数,从而检测出影像中的直线[2]。
2.相位编组法
相位编组法是一种基于梯度相位特征的直线提取方法。提出此算法的Burns等认为边缘不仅存在于灰度变化剧烈的地方,在灰度变化缓慢的地方也存在边缘[3]。不同于大多数直线提取算法,对于梯度的特征,该方法以梯度的相位而不是梯度幅度为主要的判断标准,梯度幅度只是一个辅助条件。然后根据梯度的相位信息对点进行编组,并用最小二乘法拟合出直线。
3.边缘分割法
直线作为边缘的一部分,是特殊的一类边缘特征,因此,在边缘检测的基础上进行直线提取是十分可行的。本算法在边缘检测的基础上,对边缘线进行跟踪,形成链表以获得每条线的位置、端点等信息,在清除图像中短小的边缘后,将链表中的曲线分割成直线并绘制出来,达到从影像中提取直线的目的[4]。
三、试验结果分析与比较
选用高分辨率遥感影像及人工测试影像,包含房屋、道路、裸地等地物,具有特征明显的直线,且分布均匀,数量较多,适合作为线特征提取的基础影像,如图1所示。

图1 高分辨率遥感影像
调整参数以研究每种算法的参数自适性,并从自适性、速度、稳定性、可靠性、自动化程度等5个方面对各种算法进行分析比较。
1.参数自适性
参数自适性主要是判断提取的特征对设置参数的反映程度,即参数变化对特征提取的影响程度[5]。若参数变化对特征的提取影响较大,则该算法参数自适性较弱。
(1)Hough变换
Hough变换提取直线时需要设置的参数为检测阈值T、步距θ0。其中,θ0表示直线上点的梯度方向变化的容忍范围,一般取1弧度,并不是直线提取中的决定性参数;算子中最主要的参数为检测阈值T,表1显示了在步距一定时,检测阈值T对于提取数量的影响。

表1 Hough变换参数自适性
从表1中可以看出,随着检测阈值T的改变,直线的数目有较大程度的变化,即阈值的设定对于提取结果的数目有很大影响,表明Hough变换的参数自适性较弱。
(2)相位编组法
相位编组法提取直线时需要设置的参数为检测阈值Tm、Tn。其中,Tm表示衡量梯度方向的阈值;Tn表示衡量直线支持区内,每条直线上的像素个数的阈值。表2显示了检测阈值Tm、Tn对于提取数量的影响。

表2 相位编组法参数自适性
从表2中可以看出,随着Tm、Tn中任意一个的数值改变,直线的数目都有较大程度的变化,表明相位编组法的参数自适性较弱。
(3)边缘分割法
边缘分割法提取直线时需要设置的参数为检测阈值Tm、Tn。其中,Tn表示将曲线分割成直线的阈值,并不是直线提取中的决定性参数;Tm表示衡量直线最小长度的阈值,超过这个长度的直线将被剔除。表3显示了检测阈值Tm对直线提取数量的影响。

表3 边缘分割法参数自适性
从表3中可以看出,随着Tm数值的改变,提取结果的数目有较大程度的变化,表明边缘分割法的参数自适性较弱。
通过对以上3种算法的参数自适性分析,可以得出3种算法的自适性都不是很强,每种算法之间也没有很大差别。
2.提取速度
提取速度是检测算法性能的一项重要指标。由于遥感影像的数据量大,对其进行运算的算法就更要满足一定的速度要求,否则算法的实用性就会大大降低。对试验影像进行测试,统计每种算子运算所需的平均时间,结果见表4。

表4 线特征提取算子时间
从表4中可以看出,对于相同的影像,相位编组法的速度最快,边缘分割法速度最慢。
3.稳定性
稳定性是检测算法性能的一项重要指标,是指影像的角度、噪声等对算法结果的影响程度,若在角度和噪声等因素的影响下,算法仍能提供较好的结果,则表明此算法的稳定性好[6]。算法的稳定性可以用检测算子提取特征的重复率来表示,重复率越高,算子的稳定性越好。
(1)旋转不变性
对同样的影像进行旋转,将影像进行直线提取,对于同一种算法,参数设为一致。统计每张影像上的直线数,以及与原影像相比直线重复的数目,计算成重复率,结果见表5。
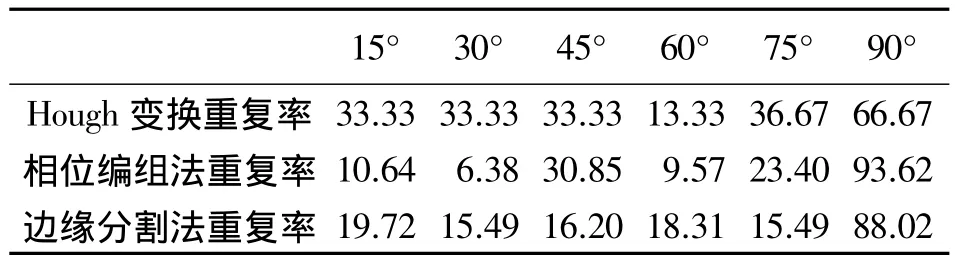
表5 线特征提取算子旋转不变性
从表5中可以看出,3种算法都比较容易受到旋转角度的影响。究其原因,Hough变换和边缘分割法中首先都要对影像边缘进行提取,而提取边缘时所用的Canny算子受影像旋转角度的影响较大,导致直线提取的结果也受到角度变化的影响。对于相位编组法,因其首先要计算梯度的方向角,而梯度的方向角是通过影像中水平和竖直方向的梯度计算而来,随着影像的旋转,水平和竖直方向的梯度自然有变化,因此计算出的梯度方向角也会随之变化,最终导致结果受到旋转角度的影响。因此,3种算法的旋转不变性都较弱。
(2)抗噪性
对同样添加了高斯噪声和椒盐噪声的影像进行直线提取,对于同一种算法,参数设为一致。结果如图2所示。

图2 高斯噪声和椒盐噪声影响下直线提取结果
从图2中可以看出,高斯噪声和椒盐噪声对3种算法都有一定程度的影响。对于高斯噪声而言,边缘分割法提取效果最好,能够提取出有效的直线,且提取错误较少;Hough变换和相位编组法的效果都不好,Hough变换提取直线的个数减少,且提取错误率增加;相位编组法虽然错误率不高,但直线的数量急剧减少。对于椒盐噪声而言,相位编组法的效果最好,在保证了提取数量的同时具有较好的可靠性;边缘分割法其次,虽然提取数量较多但错误数也很多;Hough变换的效果最差,提取出的直线基本都是错误的。
总体来说,3种算法都具有一定程度的抗噪性。其中,Hough变换和边缘分割法对高斯噪声的抵抗性更好,是因为在提取直线的过程中用到的Canny算子会进行高斯滤波;相位编组法对椒盐噪声的抵抗性更好,是因为椒盐噪声对梯度方向的影响较小。因此,在对噪声较多的影像进行直线提取前,对其进行降噪处理是十分必要的。
4.可靠性
特征的可靠性是指有效特征数占总特征数目的百分比。提取的有效特征数占总特征数目的比率越高,算法的可靠性就越好。对高分辨率遥感影像进行直线提取,统计每种算法提取出的有效直线数见表6。
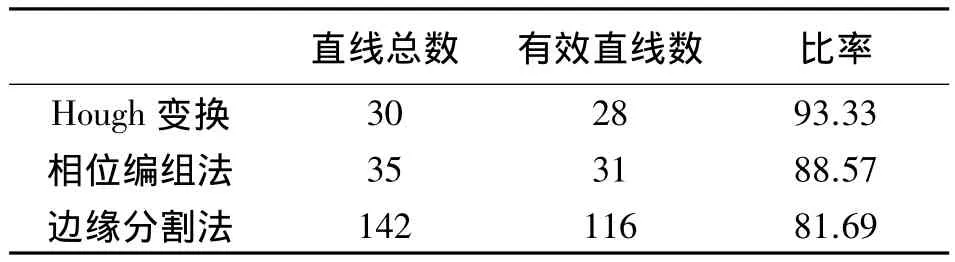
表6 线特征提取算子可靠性
从表6中可以看出,Hough变换可靠性最好,其次是相位编组法,边缘分割法的可靠性最差。相位编组法可靠性略低的原因是由于算法认为灰度变化缓慢的地方也存在边缘,以梯度的方向作为主要判断标准,若阈值设定不当,会造成提取出不明显的边缘而忽略明显边缘的情况;边缘分割法可靠性最低的原因是影像中有些地物本就不由直线构成,若强行将曲线边缘分割成直线,只会使可靠性降低。
5.自动化程度
算法的自动化程度是指运行时无须人工干预的程度。一个算法运行时需要人工干预的程度越高,它的自动化程度就越低。一般来讲,算法需要人工干预的环节是参数的设置,它直接影响了算法的自动化程度。
统计3种直线提取算法中需要人为设定的参数个数,结果见表7。

表7 线特征提取算子自动化程度
由此可知,3种算法中Hough变换的自动化程度最高,相位编组法和边缘分割法次之,3种算法都没有达到完全自动化的标准。
四、结论与展望
通过对3种直线提取算法的分析,总结出每种算法的特性:
1)Hough变换可靠性较好,自动化程度较高;有一定抵抗高斯噪声的能力;原理复杂,提取速度较慢,旋转不变性和参数自适性较弱。当对于可靠性要求较高时,适合采用此算法提取直线。
2)相位编组法原理简单,提取速度较快;有一定抵抗椒盐噪声的能力,且可靠性和自动化程度一般;旋转不变性和参数自适性较弱。当对于提取速度有较高要求时,适合采用此算法进行直线提取。
3)边缘分割法原理简单,自动化程度较高;有一定抵抗高斯噪声的能力;提取速度很慢,旋转不变性和参数自适性较弱,可靠性较差。当影像中曲线较少时适合采用此方法。
本文中研究的算法各有优劣,在实际处理图像的过程中,应当结合算法原理和使用环境,不断提高算法的适应性,针对不同大小、不同数据源的图像设定自适应阈值,才能达到理想的提取效果。总的来说,就是要从算法的参数自适性、提取速度、稳定性、可靠性和自动化程度等方面对算法进行改进,从而获得高效、稳定、有效、智能的算法。
[1]张云生,刘阳,邹峥嵘.基于Harris兴趣值的影像线特征高精度提取方法[J].测绘科学,2013,38(4):72-73.
[2]苏志祁,尉宇,王涛.改进Hough变换的算法实现[J].现代电子技术,2009,32(10):42-44.
[3]周俊,王仁礼,吴云东.基于边缘检测的编组法直线提取[J].测绘学院学报,2004,21(3):181-183.
[4]雷小奇,王卫星,赖均.一种基于形状特征进行高分辨率遥感影像道路提取方法[J].测绘学报,2009,38(5):457-465.
[5]王启春,郭广礼,查剑锋.基于图像灰度的点特征提取算子参数自适应研究[J].测绘科学技术学报,2012,29(6):435-439.
[6]余晨,金飞,石娟.基于灰度信号的点特征提取方法比较研究[J].测绘信息与工程,2009,34(6):44-45.
[7]张祖勋,张剑清.数字摄影测量学[M].2版.武汉:武汉大学出版社,2012.
[8]VON GIOI R G,JAKUBOWICZ J,MOREL J M,et al.LSD:A Fast Line Segment Detector with a False Detection Control[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(4):722-732.

