三层模型的BP网络在GNSS高程拟合中的应用研究
谭立萍,马颖异,陈永生,马洪滨
(1.辽宁省交通高等专科学校,辽宁沈阳110122;2.东北大学信息科学与工程学院,辽宁沈阳110819;3.东北大学资源与土木工程学院,辽宁沈阳110819)
一、引 言
在绝大多数还没有实现大地水准面精化的矿区及高程起伏较大的测区,目前在测绘工程施工过程中如何把GNSS观测到的大地高高精度地转换为正常高仍然是GNSS高程应用的一个重要问题。解决高程转换问题主要有两种途径:一是综合利用GNSS测量资料和地面重力观测资料,以及水准测量资料对大地水准面进行精化,进而求得高精度的正常高;二是综合利用GNSS资料和水准测量资料,通过不同的数学模型确定大地水准面高程[1]。
2000国家重力基本网均匀分布在我国国土上,并依此建立了地区绝对重力点[2],但是矿区勘探区域开采频率高、地形地质条件变化快,高程变化复杂多变,因此利用地面重力测量资料通过大地水准面精化获得地面正常高与我国目前矿山实际情况不符。
矿产资源的不断开采给矿区局部范围的重力异常短时间带来很大变化,矿区大地水准面模型应具有良好的现势性。为保证矿区大地水准面的现势性,体现矿区开采过程中地面点的实时高程,需要选择合理的模型进行矿区高程拟合。
GNSS水准测定的大地水准面因联系于国家高精度定位基准,且所含随机误差较低,以此为控制经拟合处理得到的拟合曲面,对GNSS测定正常高具有实际可操作性[3]。目前用于高程异常拟合的数学模型比较典型的是曲面拟合法[4],但曲面拟合需要较多的GNSS水准联测点才能达到一定的拟合精度,否则不能反映测区内部的复杂变化[5]。因此用数学函数去拟合测区内给定的高程异常点,拟合模型曲面仅向特定方向趋近,无法显示高程异常的复杂变化,模型误差是不可避免的[6]。
高程异常是地球重力场的参数[7],利用地球重力场模型,根据点位信息可直接求得该点的高程异常值。在一定区域内,只要有足够数量的重力测量数据,就可以比较精确地求定该区域的高程异常值[8]。一般来说,山区DTM的分辨率至少为平坦地区大地水准面分辨率的2倍甚至5倍以上[9]。
BP模型是在数学模型拟合的基础上利用BP网络自适应映射能力实现非线性运算,实现从GNSS点的平面坐标或大地坐标到GNSS点的高程异常或正常高的映射[10],这种映射能够避免人为构建数学模型带来的误差,二次拟合具有较高的精度。在施工范围较大或地形复杂的测区,由于高程异常的确定不仅取决于地球内部的密度变化,还取决于地形起伏等各种因素[11]。利用BP模型进行高程异常的拟合,可以在消除数学模型误差的基础上进行残差拟合[12],得到矿区等高程起伏较大的测区高程异常的最终数值结果。
二、BP模型的构建
为实现基于BP神经网络的GNSS高程拟合,提取平面坐标作为输入因子,高程异常ζ作为输出因子。GNSS高程拟合的数学模型可以表达为

高程异常和点位坐标(L,B)有关,若输入层取2个神经元,输出层取1个神经元,则模型2×M×1为最佳选择。
1.数据预处理
采用标准激活函数的BP神经网络需要将其标准输入、输出数据限定在[0,1]范围内,而在实际的工程应用中的目标参数数值非常大,需要将其转换为[0,1]区间的值[10-11]。为了避免输出结果接近0或1饱和区,可以将输出数据范围设定为[0.1,0.9]。
学习样本对网络进行训练前,需要对数据进行归一化处理,经纬度为学习样本中的输入因子,输出因子为高程异常。
对GNSS数据的大地经纬度和高程异常值进行归一化处理的公式为
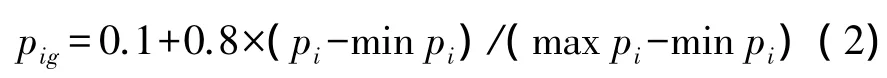
式中,pi为输入目标;pig为输出目标;max pi、min pi分别为输入目标的最大值和最小值。
2.中间层神经元数选取
采用单中间层的BP网络进行高程拟合函数逼近,由于输入层有2个神经元,输出层只有1个神经元,则中间层神经元个数M应该位于 5,20[ ]范围内。中间层神经元个数很难确定,而这很大程度上影响着网络的预测性。
本试验首先取15个神经元,分别从不同的BP网络训练算法、测试集均方误差与平均误差、网络权值调整次数等4个方面考察神经网络性能;之后分别取 6、8、12、15、18、20 个,并与此时的预测性能进行比较,检验中间层神经元个数对网络性能的影响。当BP神经网络预测误差最小时,网络中间层的神经元数目最佳。
3.神经元上传递函数
传递函数是BP网络的重要组成部分,传递函数又称激活函数,必须是连续可微的。按照BP网络设计原则,中间层神经元的传递函数为S型正切函数。如果将网络的输出层设定为purelin线性传递函数,那么整个网络的输出可以取任意值。由于输出已被归一化到区间[0,1]上,因此,输出层神经元的传递函数可以设定为S型对数函数。
通过多次试验与数据分析,得到高程异常BP神经网络拟合的中间层神经元的传递函数为S型正切函数,输出层神经元的传递函数设定为S型对数函数。
4.网络学习函数
对于2×M×1网络结构,采用梯度下降动量学习函数进行网络学习,计算权值或阈值的变化率。通过对本文涉及的数据进行试验发现,对于不同的数据实例和不同的网络结构,权值与阈值的最佳取值均不尽相同,本试验采取随机数值进行网络训练。
5.训练函数
对于高程拟合BP网络的训练,分别采用梯度下降法(traingd)、拟牛顿算法(trainbfg)、动量及自适应lr的梯度下降训练法(traingdx)、Levenberg-Marquardt训练法(trainlm)4种方法进行网络训练。
三、BP模型拟合精度分析
以辽宁某矿区(高山区)GNSS点和水准资料作为样本来源,测区比高达1400多米,测区所涉及范围达上千平方千米,项目搜集和施测了40多个等级水准点作为样本点进行BP高程异常拟合检验,选择测区中均匀分布并代表地势变化特征点为学习样本,其余点为测试样本进行训练。
1.方案1
学习样本6,测试数据为9,中间层设定12,网络目标0.000 1。采用梯度下降法(traingd)、拟牛顿算法(trainbfg)、动量及自适应的梯度下降训练法(traingdx)、Levenberg-Marquardt训练法(trainlm)进行网络训练,结果见表1。通过方案1可以分析得到如下结论:高程异常BP神经网络拟合训练函数比较好的是动量及自适应的traingdx梯度下降训练法,其次是trainlm Levenberg-Marquardt训练法。
2.方案2
学习样本数为8,测试数据为7,中间层分别为6、8、12、15、18、20 个,训练函数先后采用 traingdx 梯度下降训练法和trainlm Levenberg-Marquardt训练法,训练目标为0.000 1。训练结果见表2。
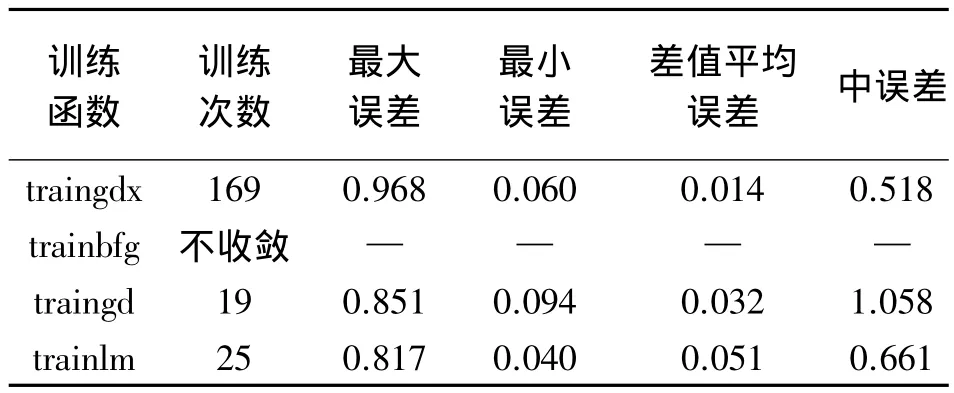
表1 误差对比 m
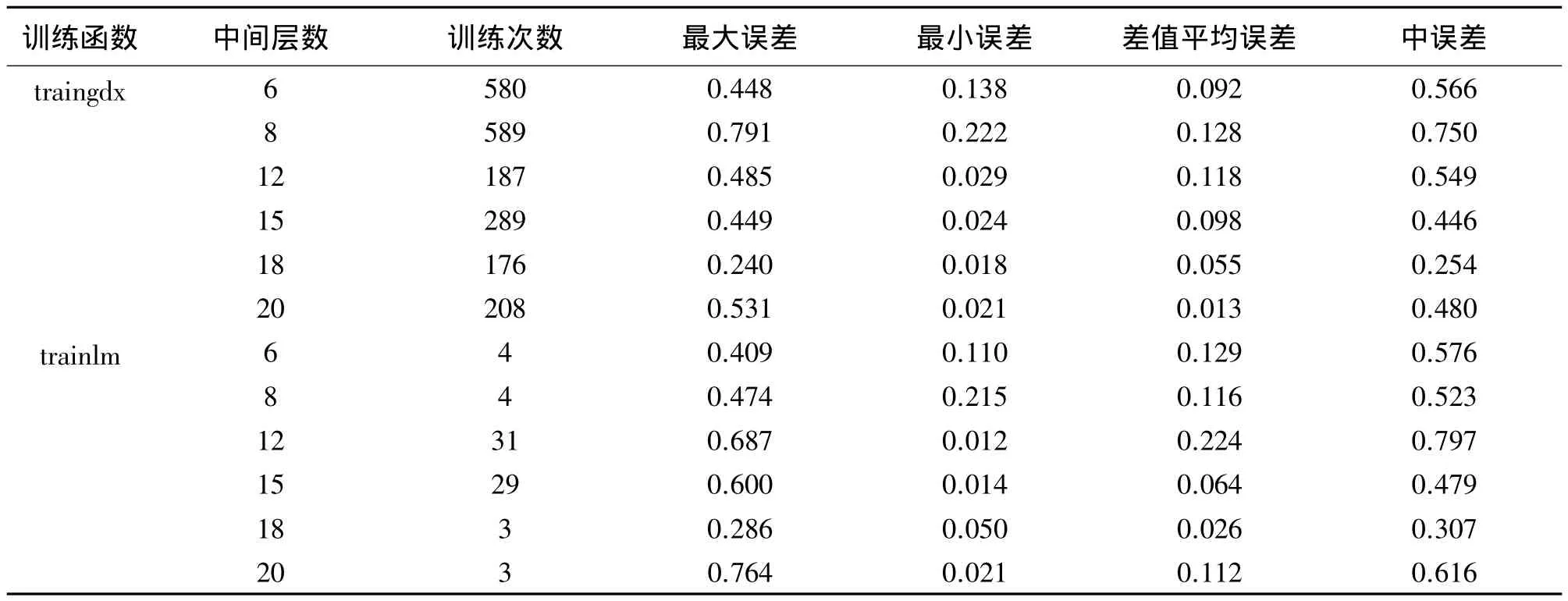
表2 误差对比 m
通过方案2可以得到如下结论:通过对高程异常BP的拟合,对精度而言,traingdx函数表现效果最好,对收敛速度而言,trainlm函数收敛速度最快。随着中间层神经元个数的增加,拟合精度提高,但并非中间层神经元数越多拟合精度就越高。
在山区进行BP神经网络高程异常的拟合,选用不同的训练函数对精度和收敛速度有一定的影响。通过对高程异常进行BP模型拟合,训练函数中动量及自适应lr的traingdx梯度下降训练法网络精度好,trainlm Levenberg-Marquardt训练法训练速度快。本次试验训练选择traingdx,中间层选择18层,高程异常外符合精度可以满足山区五等水准测量要求(如图1、图2所示)。网络训练中,随着中间层神经元个数的增加,拟合精度提高,但并非中间层神经元数越多拟合精度就越高,通过试验数据分析,在山区中间层可选择15或18个神经元。
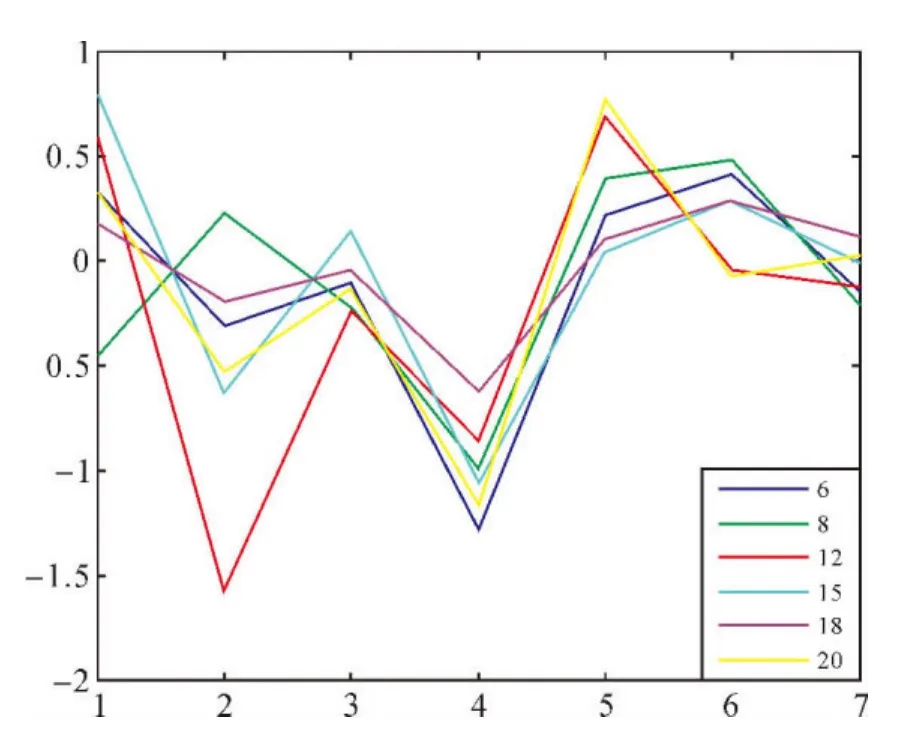
图1 梯度下降拟合误差比较
在工程实践中,应进行多次试算,选择合适的拟合函数,确定合理的网络结构,以寻求最优的网络拓扑结构。
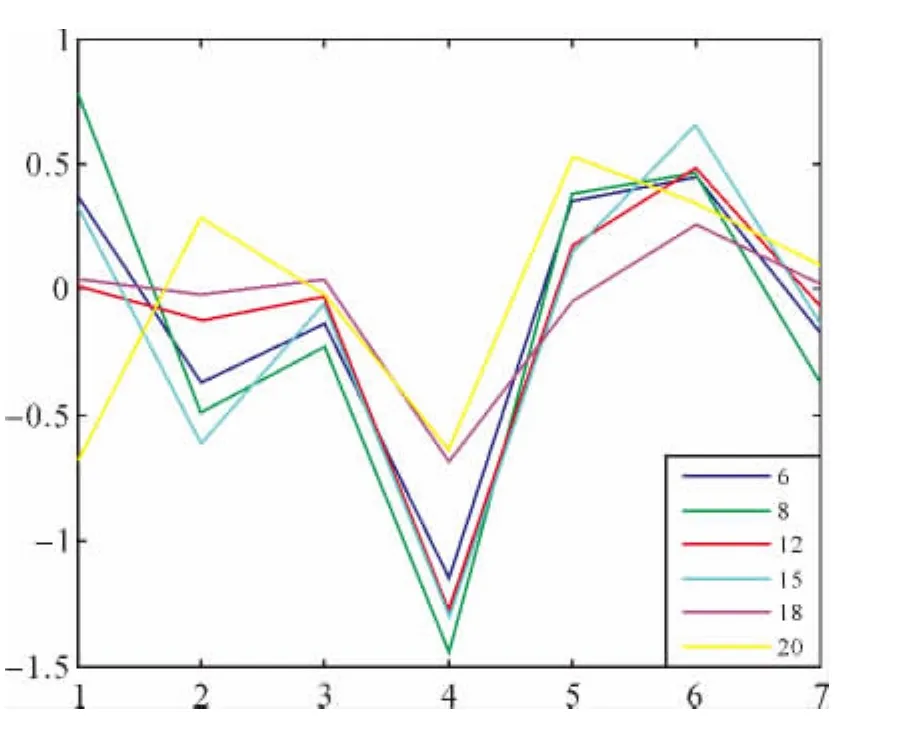
图2 L-M拟合误差比较
四、结 论
1)BP方法采用非线性拟合方法完成区域似大地水准面的拟合,其数据更贴近多变的似大地水准面,因而可达到较高的拟合精度。计算结果表明,利用BP方法转换GNSS高程时,采用2×M×1的网络结构,选用traingdx梯度下降训练法作为训练函数效果最佳,拟合精度好于其他训练函数。
2)BP模型在已知点少、地势变化复杂的山区、矿区进行高程拟合更具有实际意义。并且采用梯度下降训练法和Levenberg-Marquardt训练法时,拟合误差图走势基本一致,这表明两种训练法在拟合精度方面具有同等作用。
3)采用BP模型进行高程拟合的精度与中间层神经元数相关,由试验结果分析可知,当中间层神经元数目接近学习样本数2倍的情况下其拟合精度有望达到最优。因此,在应用BP模型时,建议其中间层神经元数尽量达到学习样本数的2倍。
[1]陈俊勇,李建成,宁津生,等.中国新一代高精度、高分辨率大地水准面的研究和实施[J].武汉大学学报:信息科学版,2001,26(4):283-289.
[2]JACOB T,WAHR J,GROSS R,et al.Estimating Geoid Height Change in North America:Past,Present and Future[J].Journal of Geodesy,2012,86(5):337-58.
[3]李建成.最新中国陆地数字高程基准模型:重力似大地水准面 CNGG2011[J].测绘学报,2012,41(5):651-660,669.
[4]陈俊勇,杨元喜,王敏,等.2000国家大地控制网的构建和它的技术进步[J].测绘学报,2007,36(1):1-8.
[5]马洪滨,董仲宇.多面函数GPS水准高程拟合中光滑因子求定方法[J]东北大学学报:自然科学版,2008,29(8):1176-1179.
[6]曹先革.基于人工神经网络的GPS高程异常拟合方法研究[D].北京:中国地质大学,2008.
[7]HORWATH M,LEMOINE J M,BIANCALE R,et al.Improved GRACE Science Results after Adjustment of Geometric Biases in the Level-1B K-band Ranging Data[J].Journal of Geodesy,2011,85(1):23-38.
[8]刘成龙,杨天宇.基于BP神经网络的GPS高程拟合方法的探讨[J].西南交通大学学报,2007,42(2):148-152.
[9]鲁铁定,周世健,臧德彦.关于BP神经网络转换GPS高程的若干问题[J].测绘通报,2003(8):7-10.
[10]WEST B P,SEMPERE J C.Gravity Anomalies,Flexure of Axial Lithosphere,and along-axis Asthenospheric Flow Beneath the Southeast Indian Ridge[J].Earth and Planetary Science Letters,1998,156(3-4):253-66.
[11]罗志才,陈永奇,宁津生.地形对确定高精度局部大地水准面的影响[J].武汉大学学报:信息科学版,2003,28(3):340-344.
[12]张小红,程世来,许晓东.基于Kriging统计的GPS高程拟合方法研究[J].大地测量与地球动力学,2007,27(2):47-51.

