广义交叉准则与有偏估计下的坐标重心化转换模型

王 仁，赵长胜

(江苏师范大学城建与环境学部，江苏徐州221116)

一、引 言

GPS技术的不断发展，使其在测绘领域的应用越来越广。但是GPS测量成果建立在WGS-84坐标系下，属于地心坐标系，而现有的很多测绘成果大多采用的1954北京坐标系、1980西安坐标系和地方独立坐标系，均属于参心坐标系。为了将GPS所测成果应用于工程应用，需进行坐标转换，转换为相应的参心坐标系。

比较常用的坐标转换模型有布尔莎模型、莫洛金斯基模型和武测模型等。其中，布尔莎模型比较适用于大范围小角度的坐标转换，对于小范围区域，公共点之间相距比较近，所求得的平移参数和旋转参数会有很强的相关性，从而导致法方程系数阵病态，导致所求平移参数值和旋转参数值有较大误差［1］。用坐标重心化转换模型可以有效降低法方程系数阵的病态严重性，但经过转换后法方程系数阵依然存在病态性，而广义交叉准则可以有效解决法方程系数阵的病态性。结合有偏估计基本原理，基于广义交叉准则与有偏估计的坐标重心化转换模型可以明显提高小范围区域内坐标转换的精度，也证明了此模型适用于小范围区域的坐标转换。

二、布尔莎模型

坐标转换经常采用布尔莎模型，该模型共有7个参数，分别是 3个平移参数(ΔX，ΔY，ΔZ)、3个旋转参数(εX，εY，εZ)和1个尺度比参数 k。其坐标转换方程式如下

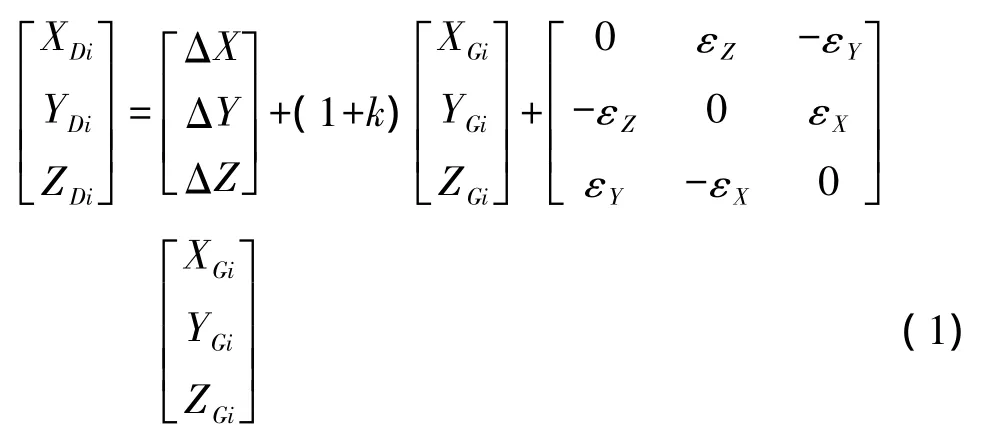
式中，(XDi，YDi，ZDi)和(XGi，YGi，ZGi)分别为空间直角坐标系ODiXDiYDiZDi和OGiXGiYGiZGi中的空间直角坐标。式(1)写成误差方程式为

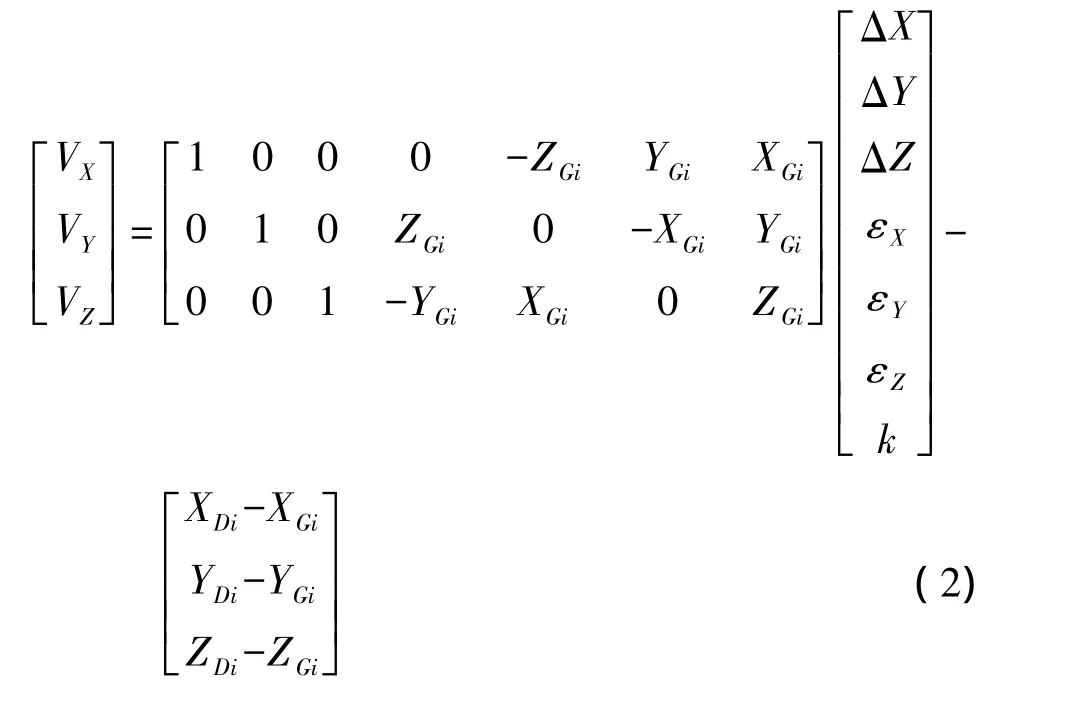
写成矩阵形式为

由于坐标转换中各观测值相互独立，故可设权阵P=I。根据最小二乘原理可以得到

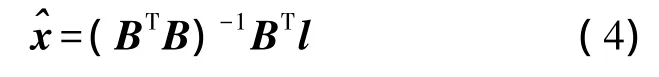
其单位权中误差为

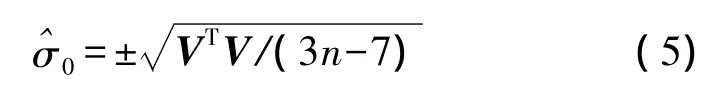
式中，n为公共点的个数。

三、基于广义交叉准则与有偏估计的坐标重心化转换模型

1.坐标重心化转换模型

使用布尔莎模型求解小范围区域坐标转换参数时，误差方程常数项矩阵整体很小，而误差方程系数项矩阵整体很大，从而导致法方程系数阵的病态。因此，可以找到一个平衡点，用公共点的坐标减去平衡点的坐标，以减小其过大的坐标数据，即可以在坐标转换之前，先对两套公共点的坐标进行重心化，得到其对应的重心坐标，以降低法方程的病态性。设(Xi重，Yi重，Zi重)是坐标系 i(i=Di，Gi)公共点的重心坐标，若公共点的个数为n，则

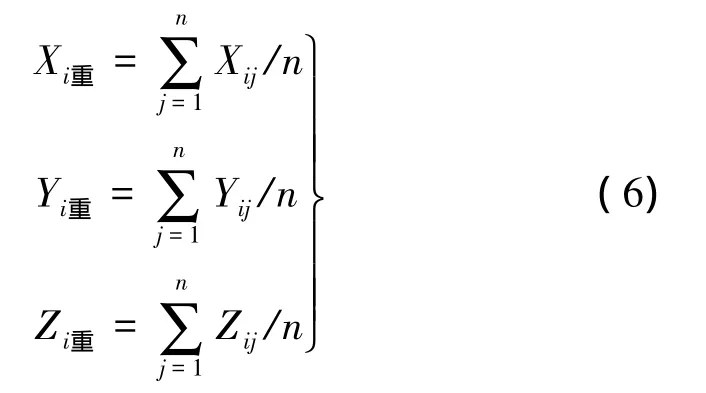
利用所求得的重心坐标求出各个公共点的重心坐标(XZij，YZij，ZZij)

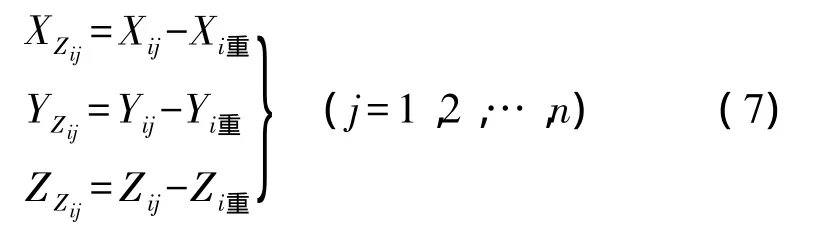
通过以上的坐标重心化转换，得到两组公共点的新坐标。由这两组新坐标组成误差方程式(2)，根据本算例的数据，法方程的条件数明显下降，根据文献［2］的理论可知法方程依然存在病态性。

2.基于广义交叉准则的坐标重心化转换模型

如果可以找到一个正则参数α对法方程系数阵进行改正，则可有效解决法方程的病态问题。根据文献［2］，广义交叉准则(GCV)的函数为

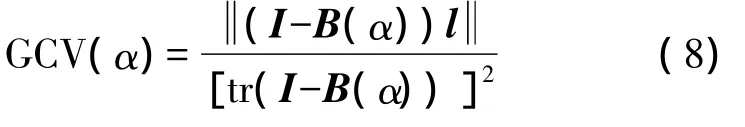
式中，I为与 B(α)同阶的单位矩阵;B(α)=B(BTPB+αI)－1BT;l为常数项矩阵;tr()表示求矩阵的迹。这样可取函数GCV(α)为最小值时对应的α作为正则参数。而此时法方程变为

则转化为用有偏估计来求解转换参数。

3.基于广义交叉准则与有偏估计的坐标重心化转换模型

(1)岭估计

对于高斯-马尔可夫模型，岭估计由 A.E.Hoerl和 R.W.Kennard于1970年定义为

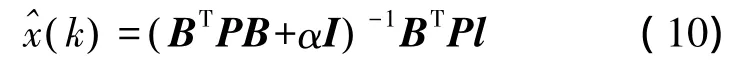
式中，α≥0为常数，称为岭常数，亦即上面所求正则参数;I为与BTPB同阶的单位矩阵。给定不同的α值，由式(10)可以求出不同的估值。很明显，当α=0时，岭估计即为最小二乘估计，因此，最小二乘估计是岭估计的一个特例，岭估计是最小二乘估计的延伸。对于本文中的B矩阵为病态矩阵，BTPB是奇异的，无法对其正常求解，通过广义交叉准则总能找到一个合适的α值，使BTPB+αI的奇异程度有所降低，便于下一步的求解。

(2)谱修正迭代法

根据式(3)，其法方程可写成

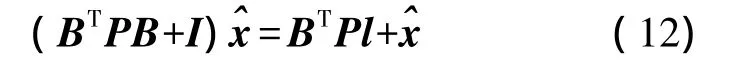
式中，I为与BTPB同阶的单位矩阵。

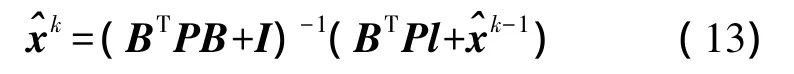
若令

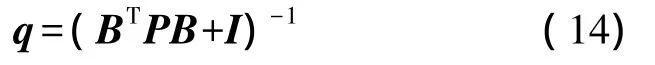
则式(13)又可以写为

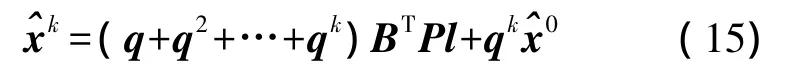
四、精度评定

坐标转换的精度可以从转换参数的精度和转换模型的精度分别进行考虑，可以根据式(5)求出转换参数的精度，即单位权中误差，转换模型的精度包括模型的内符合精度和模型的外符合精度。

设有n个公共点，m个检核点。模型内符合精度是先根据用公共点求得的转换参数计算公共点在相应坐标系的坐标与在该坐标系下原始坐标间的残差V，再通过式(16)计算得到

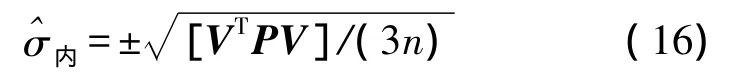
模型外符合精度是根据求得的转换参数计算检核点的坐标与原测坐标间的残差V'通过式(17)计算得到

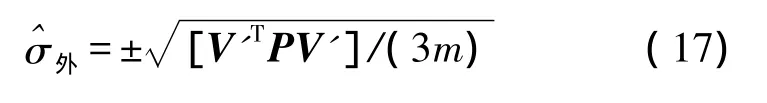
五、算例与分析

10个分别在WGS-84坐标系下和1980西安坐标系下的坐标见表1。取其中的7个点作为求解转换参数的转换公共点，其点号分别为 1、2、3、5、7、8、9，其余 3个点(即 4、6、10)作为检核点，且这 3个检核点在由7个公共点所建立的范围之内。

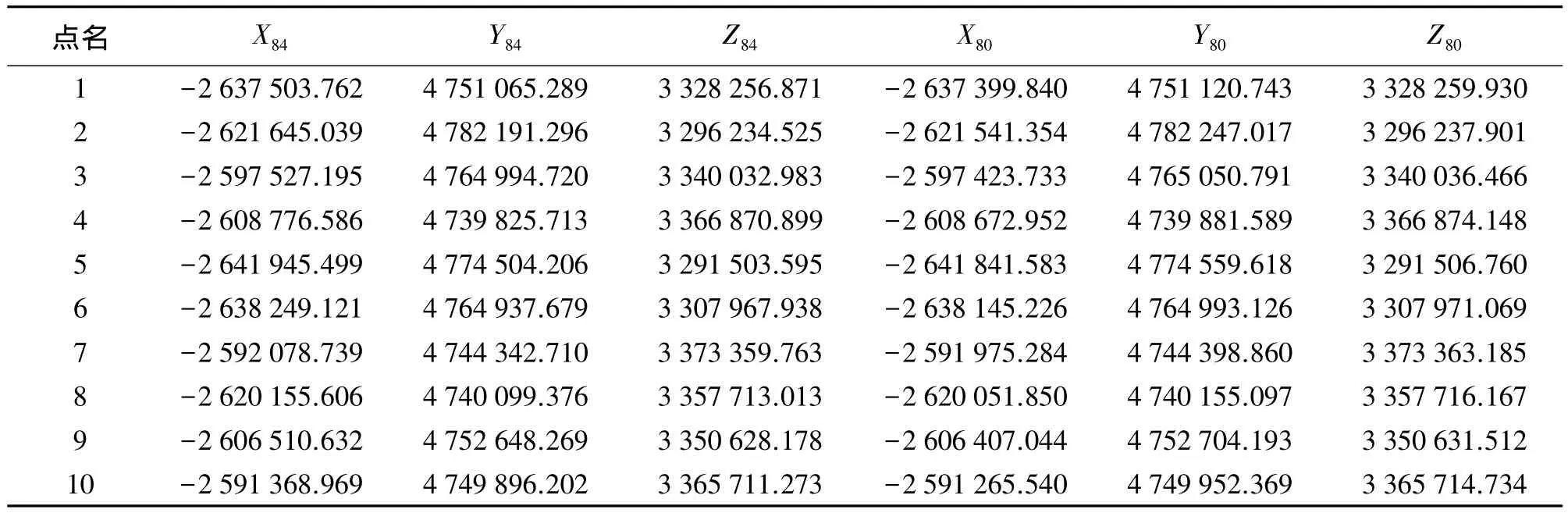
表1 对应点坐标 m

表2列出了两种有偏估计方法求解转换参数的单位权中误差、模型内符合精度和模型外符合精度。从表中的数据可以看出，转换模型的精度都相当好，与文献［1］的精度相当。

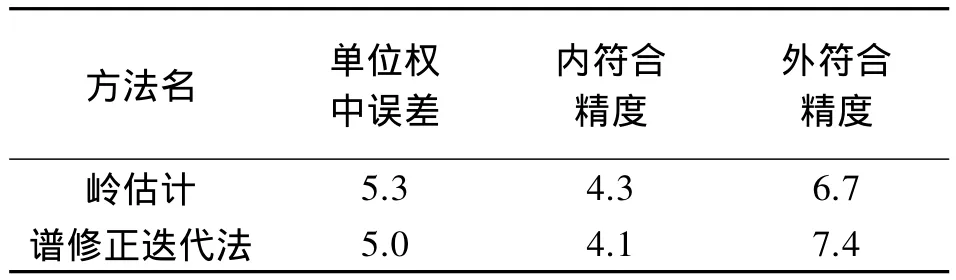
表2 不同方法及其精度 mm

表3列出了3个检核点的坐标差值，该坐标差值由检核点转换后坐标与原测坐标相减求得。从表中的数据可以看出，与文献［1］的精度相当。

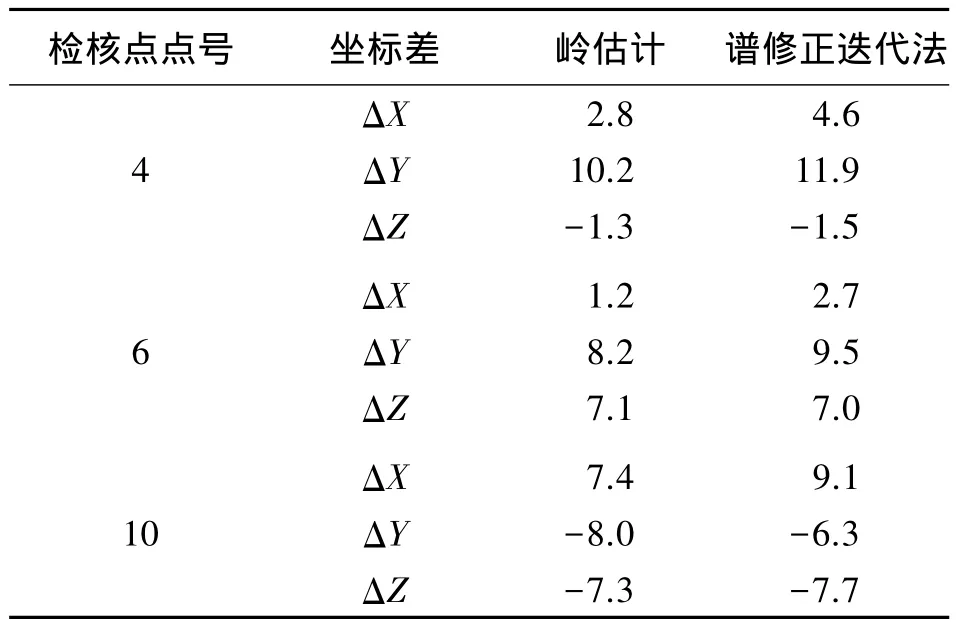
表3 检核点坐标差值 mm

六、结束语

本文研究了一种法方程病态的小范围区域坐标转换模型——基于广义交叉准则与有偏估计的坐标重心化转换模型。试验结果表明:

1)坐标重心化可以降低法方程的病态性。

2)广义交叉准则可以有效解决法方程的病态性。

3)根据有偏估计的基本原理可以有效提高坐标转换的精度。

4)基于广义交叉准则与有偏估计的坐标重心化转换的布尔莎模型可以进行小范围区域的坐标转换。

［1］董杰，岳建平.基于抗差估计的坐标重心化转换模型［J］.测绘通报，2012(7):39-42.

［2］卢秀山，冯遵德，刘纪敏.病态系统分析理论及其在测量中的应用［M］.北京:测绘出版社，2007:12-13，71-72.

［3］武汉大学测绘学院测量平差学科组.误差理论与测量平差基础［M］.武汉:武汉大学出版社，2009:157-158.

［4］徐绍铨，张华海，杨志强，等.GPS测量原理及应用［M］.武汉:武汉大学出版社，2008:26-27.

［5］赵长胜.测量数据处理理论与方法［M］.北京:测绘出版社，2012:169-173.