浅海水下机器人耐压壳体的优化设计

鲍维俊

摘 要：浅海水下机器人的耐压壳体是水下机器人的重要部件之一。本文在对水下机器人的耐压壳体的失效形式进行理论分析基础上，提出优化设计的数学模型。借助MATLAB优化工具对耐压壳体进行优化设计。

关键词：水下机器人；耐压壳体；优化设计

DOI：10.16640/j.cnki.37-1222/t.2015.24.212

0 引言

水下机器人的耐压壳体用来装置电子元器件和检测装置，耐压壳体形状常采用重量与排水量比值较小的球形和圆柱形，对于对浅海水下机器人的耐压壳体一般选择薄壁圆柱形壳体。

1 理论分析

对于耐压壳体等薄壁圆柱壳体，其失效形式主要有强度破坏和失稳破坏两种。强度破坏是指耐压壳体的某些受力点达到屈服状态，产生塑性变形而导致结构破坏。失稳破坏是指耐压壳体内部应力在未达到材料的强度极限的情况下，产生较大的变形而使结构降低承载能力，甚至发生破坏[1]，本文着重考虑长圆柱耐压壳体的情况。

长圆柱壳体可以忽略两端边界对稳定性的影响，其失效形式为外压壳体失稳。长圆柱壳体临界压力计算，工程上采用著名的Bresse公式[2]：

（1）

其中：Pcr为壳体接近破坏时的临界压力（MPa）； E为壳体材料的弹性模量（MPa）；μ为壳体材料的泊松比；T为壳体的壁厚（mm）；D为壳体的平均值直径（mm）；L为壳体的长度（mm）。

2 数学建模

2.1 优化模型

本文对对耐压壳体重量与排水量比进行优化，这种优化问题的数学模型一般表达式写成

minF（x） s.t. G（x）≥0 （2）

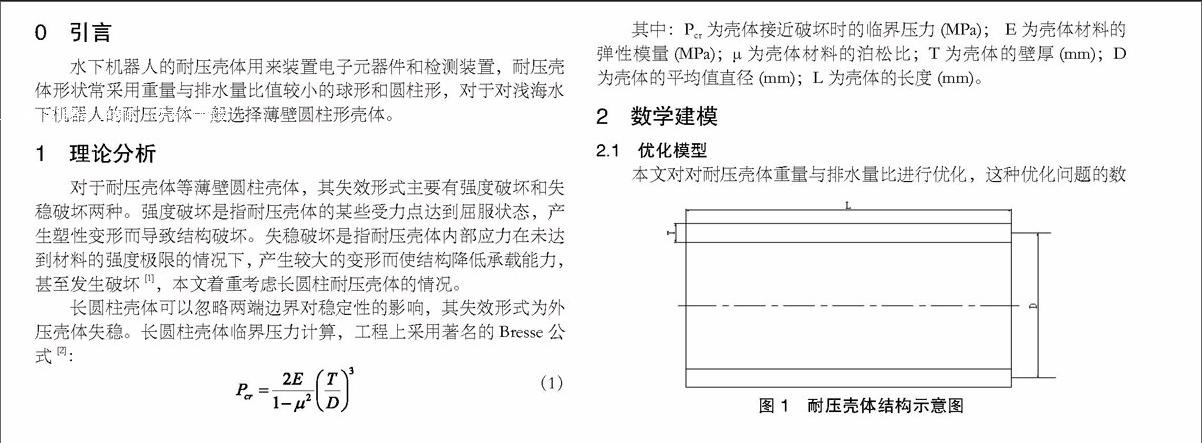
（1）确定设计变量。图1为耐压壳体结构示意图，在本文中，圆柱耐压壳体的长度L为定值。圆柱耐压壳体的设计变量共2个，分别为圆柱耐压壳体的壁厚T和圆柱耐压壳体的中面直径D。

（2）确定目标函数。本文以耐压壳体重量与排水量比为优化问题的目标函数。

圆柱耐压壳的重量为： W=ρπDTL （3）

圆柱耐压壳的排水量为： （4）

耐压壳体重量与排水量比为： （5）

其中：W为圆柱壳体的重量；D为耐压壳的排水量；ω为耐压壳体重量与排水量比值；ρ为圆柱壳体材料密度；ρw为海水密度；圆柱耐压壳体的中面直径D；圆柱耐压壳体的壁厚T；圆柱耐压壳体的长度L。

（3）确定约束函数。圆柱耐压壳体的结构优化问题的约束函数为以下两个条件：

1）薄壁条件： （6）

2）稳定性条件：SAPW-Pcr≤0 （7）

其中，Pcr为耐压壳体的临界强度，PW为ROV的工作深处静水压力，SA为安全系数。

2.3 数学模型求解

耐压壳体的长度限定，所以耐压壳体的优化设计为典型的二维变量非线性约束的优化问题，MATLAB优化工具箱可以方便解决此类问题。

3 实例分析

假设水下机器人工作深度范围为100m～1500m，圆柱壳体长度L=800mm。研究三种不同材料的耐压壳体的结构，三种材料分别为：某种铝合金，某种钛合金和某种合金钢。

本文中设计的耐压壳体安装在ROV的浮力材料中，与设计的浮力材料的尺寸相关。可以得到估计相应的取值范围，圆柱耐压壳体的壁厚T，取值范围4～10mm，圆柱耐压壳体的中面直径D，取值范围160～180 mm。

设圆柱壳体为长圆柱壳体。Pcr可以根据式（1）进行计算。运用matlab优化工具箱来求解约束非线性规划问题。不同材料的计算结果，见图2、图3、图4和图5。

图2给出了三种不同材料的耐压壳体不同工作深度的最优壁厚，从图上可以看出，工作深度500米及以上，耐压壳体的壁厚基本上与工作深度成线性关系（起始点除外，由于设计尺寸的限制），材料的密度越小，随着工作深度的不断增加，壁厚增加幅度越大。反之，增加越平缓。

图3给出了给出了三种不同材料的耐压壳体不同工作深度的最优的中面直径，由于受到设计尺寸的限制，起始的耐压壳体的中面直径很大，随着工作深度的不断增加，中面直径恢复平缓上升。对于合金钢，弹性模量和密度大，随着工作深度增加，中面直径几乎保持不变；对于铝合金，弹性模量和密度小，随着工作深度增加，工作深处静水压力不断增加，壁厚和直径比不断变大，中面直径变化量大于壁厚的变化量；对于钛合金，介于两者之间。

图4给出了三种不同材料的耐压壳体不同工作深度的最优结构的重量，从图上可以看出，工作深度500米及以上，耐压壳体的重量基本上与工作深度成线性关系（起始点除外，由于设计尺寸的限制），材料的密度越小，随着工作深度的不断增加，增加幅度越大。反之，增加幅度越小。

图5给出了三种不同材料的耐压壳体不同工作深度的最优结构重量与排水量之比，铝合金的重量与排水量之比最小，合金钢金的重量与排水量之比最大，钛合金介于两者之间。在相同工作深度下，铝合金耐压壳体的重量与排水量之比最小，承载能力最强。

4 结论

本文讨论了等薄壁圆柱耐压壳体的三种不同形式的失效形式，然后对耐压壳体重量与排水量比为优化问题的进行了研究，深入细致地讨论了三种不同材料的耐压壳体，在不同工作深度（100～1500m）情况下的理论上的最优结构，耐压壳体的结构与材料的密度和弹性模量有着密切的关系。随着ROV工作深度的不断增加，耐压壳体的结构尺寸不断变化。根据ROV的工作深度和结构尺寸，来选择耐压壳体的材料，以此来设计出耐压壳体的最优结构。

参考文献：

[1]程浩.基于MATLAB和Creo的浮标耐压壳体设计[J].制造业自动化，2013（20）：127-129.

[2]蒋新松，封锡盛，王棣棠.水下机器人[M].沈阳：辽宁科学技术出版社.endprint