基于RBF神经网络结构混合优化的数字识别
张秀玲,付 栋,李海滨,来永进,王振臣
(1.燕山大学河北省工业计算机控制工程重点实验室,河北秦皇岛 066004;
2.国家冷轧板带装备及工艺工程技术研究中心,河北秦皇岛 066004)
基于RBF神经网络结构混合优化的数字识别
张秀玲1,2,付栋1,李海滨1,来永进1,王振臣1
(1.燕山大学河北省工业计算机控制工程重点实验室,河北秦皇岛066004;
2.国家冷轧板带装备及工艺工程技术研究中心,河北秦皇岛066004)
摘要:以数字识别为应用背景构建RBF神经网络结构,首先把最近邻聚类算法与k-均值聚类算法应用于RBF神经网络隐层中心个数及中心值的确定中,实现了隐层中心个数与中心值的自适应获取;然后将遗传算法与伪逆法相结合来确定隐层中心宽度及输出权值;最后对混合优化的神经网络与传统的基于中心自组织学习算法优化的网络进行仿真实验.实验中使用未加噪声和添加噪声的数字样本对网络进行测试,与传统优化方法对比结果表明,应用该混合学习算法构建的神经网络具有识别能力强、计算量小的优点.
关键词:径向基函数神经网络(RBFNN); 聚类; 遗传算法; 数字识别
数字识别是图像字符识别(ICR)的一个重要分支,是图像处理技术和模式识别技术相结合的研究课题.随着国家信息化进程的加速,其在车牌号码、身份证号码、邮政编码及其他编号识别方面具有重要的使用价值.目前数字识别常用的方法包括基于模板匹配、特征匹配和神经网络的方法.在基于神经网络的方法中,由于径向基函数神经网络(RBFNN)具有非线性逼近能力强、结构简单、学习速度快等优点,因而被广泛应用于模式识别领域[1].
然而有效确定RBF神经网络的隐层参数是其难点所在,这包括隐层节点数目、隐层中心值和中心宽度的确定.在隐层的三个参数中,隐层节点的数量决定了网络的复杂度,过多或者过少的隐节点数目都会降低网络的泛化能力;隐层中心值的确定最为关键,不恰当的中心值无法实现从非线性输入空间到线性输出空间的转换;隐层中心宽度也是影响网络分类能力的重要因素,宽度过大,类与类之间的界限模糊,分类精度不高,宽度过小,核函数覆盖的区域就小,网络泛化能力就差[2].
根据隐层中心值的确定方法不同,常用的RBF神经网络学习算法有中心自组织选择算法和有监督选择中心的算法.其中中心的自组织选择算法是一种混合学习算法,包含自组织学习阶段和监督学习阶段.自组织学习阶段通常采用k-均值等聚类算法确定隐层中心值,然后通过式(1)求得中心宽度.
式中:σ是中心宽度;d为任意两中心值的最大距离;m为中心个数,监督学习阶段通常采用最小二乘法来确定权值[3];而有监督选择中心的算法中神经网络的所有参数都进行有监督的学习过程,通常采用基于梯度下降的误差纠正算法来实现[4].
在中心自组织选择算法中,k-均值聚类算法需要人为确定聚类数目及初始聚类中心值,且聚类结果严重依赖于初始聚类中心值的选取,而通过公式求取中心宽度的方法又依赖于聚类中心值,因此若中心值不准确,那么整个网络分类效果就会受到较大影响.针对上述问题,本文应用最近邻聚类算法与k-均值聚类算法相结合的方法来确定隐层中心值,从而避免了人为因素对结果的干扰;运用遗传算法与伪逆法确定隐层中心宽度和输出权值,使中心宽度达到全局最优.该混合方法过程简单,计算量小.在数字识别的仿真试验中,用该算法设计的神经网络识别精度高、泛化能力好,从而证明了此方法的有效性.
1 数字字符的特征提取
车牌识别系统主要包括三个模块,分别是车牌定位[5]、字符分割和字符识别[6],其识别流程如图1所示.本文对车牌中的数字进行识别,将拍摄质量较好的图像进行车牌定位、字符分割、字符图像归一化、二值化等操作后(结果如图2所示),得到像素为32×16的数字二值图像共计100张,样本如图3所示.
在对数字进行识别前,首先要对待识别的字符进行特征提取.字符的识别特征可以分为结构特征和统计特征.本文选择统计特征中的粗网格特征提取法提取数字特征.
以图2中数字0为例,
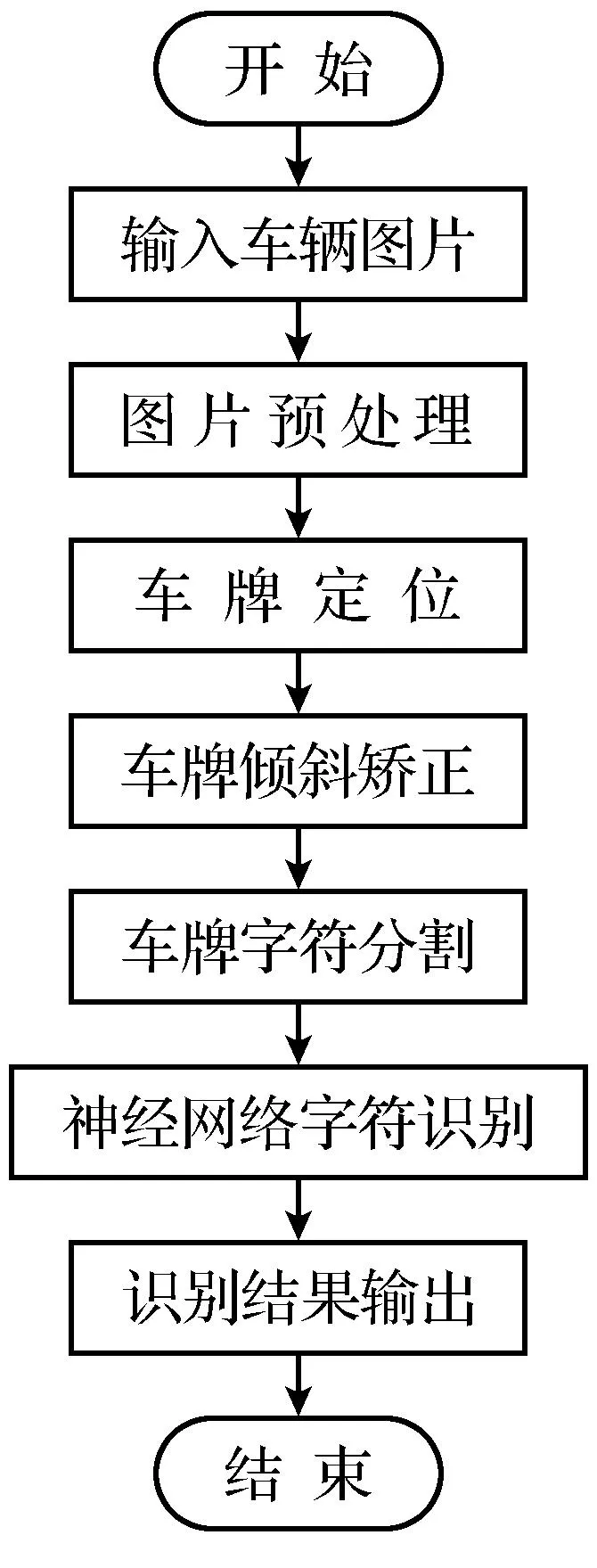
图1 车牌识别流程
其过程为:
(1) 首先将图像分割成8×4个网格,如图4

图2 车牌处理

图3 数字样本
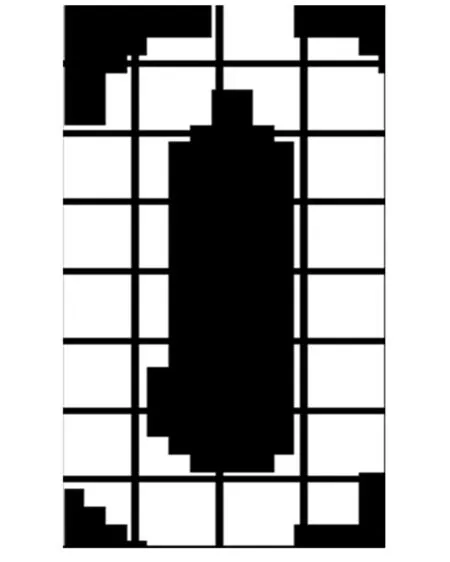
图4 加网格的数字0
所示.
(2) 从左到右,从上到下依次统计每个网格内白色像素点的个数,并将其组成一个32维的特征向量.经统计得图2中数字0的特征向量为
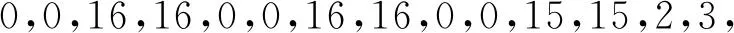
在粗网格特征提取后,为了消除各特征之间量纲、量级等不同的影响,且使各个指标具有可比性,需要对原始数据进行归一化处理.常用的归一化方法有最值法与和值法,分别如式(2)、式(3)所示.

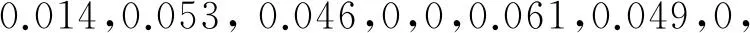
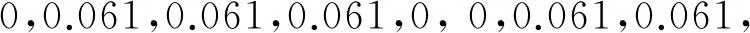
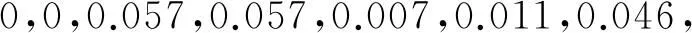
2 基于聚类、遗传算法的RBF神经网络
混合优化设计
2.1RBF神经网络的结构及原理
RBF神经网络是一种三层的前向神经网络,由输入层、隐含层、输出层构成.输入层是把输入向量简单地映射到隐含层,并不对数据作任何处理;隐含层通过径向基函数对输入进行处理,实现输入层到隐含层的非线性映射,径向基函数具有对中心点径向对称且衰减的非负特性,属于局部响应函数;隐含层的输出通过权值与输出层连接,实现隐含层到输出层的线性映射.RBF神经网络的结构拓扑图如图5所示.

图5 RBF神经网络结构拓扑图
图5中,ri(x)表示径向基函数,通常选择高斯函数作为隐层节点的激活函数,如式(4)所示:
式中: x=(x1,x2,…,xn)是n维输入向量;ci是第i个基函数的中心, 是与x具有相同维数的向量;σi表示基函数的中心宽度; ‖x-ci‖表示x与ci之间的欧氏距离.ri(x)在ci处有唯一的一个最大值, 随着‖x-ci‖的增大,ri(x)迅速衰减到零.
从以上叙述中可以得出,输入层实现从x到ri(x)的非线性映射,输出层实现从ri(x)到yk的线性映射,网络输出为:
式中,yk表示输出层第k个节点的输出,p是输出节点的个数,wik是第i个隐层节点与第k个输出层节点的连接权值,m表示隐层节点个数.
2.2最近邻聚类算法确定隐层中心个数
应用最近邻聚类算法[7]的优点在于隐层中心的个数不需要事先确定,它可以在训练过程中自动调节,下面给出这种算法的简要描述:
(1) 根据样本数据选择一个适当的宽度r,定义一个矢量c(i)用于统计聚类中心;
(2) 从第一个样本数据x1开始,以x1建立一个聚类中心,并令c(1)=x1;
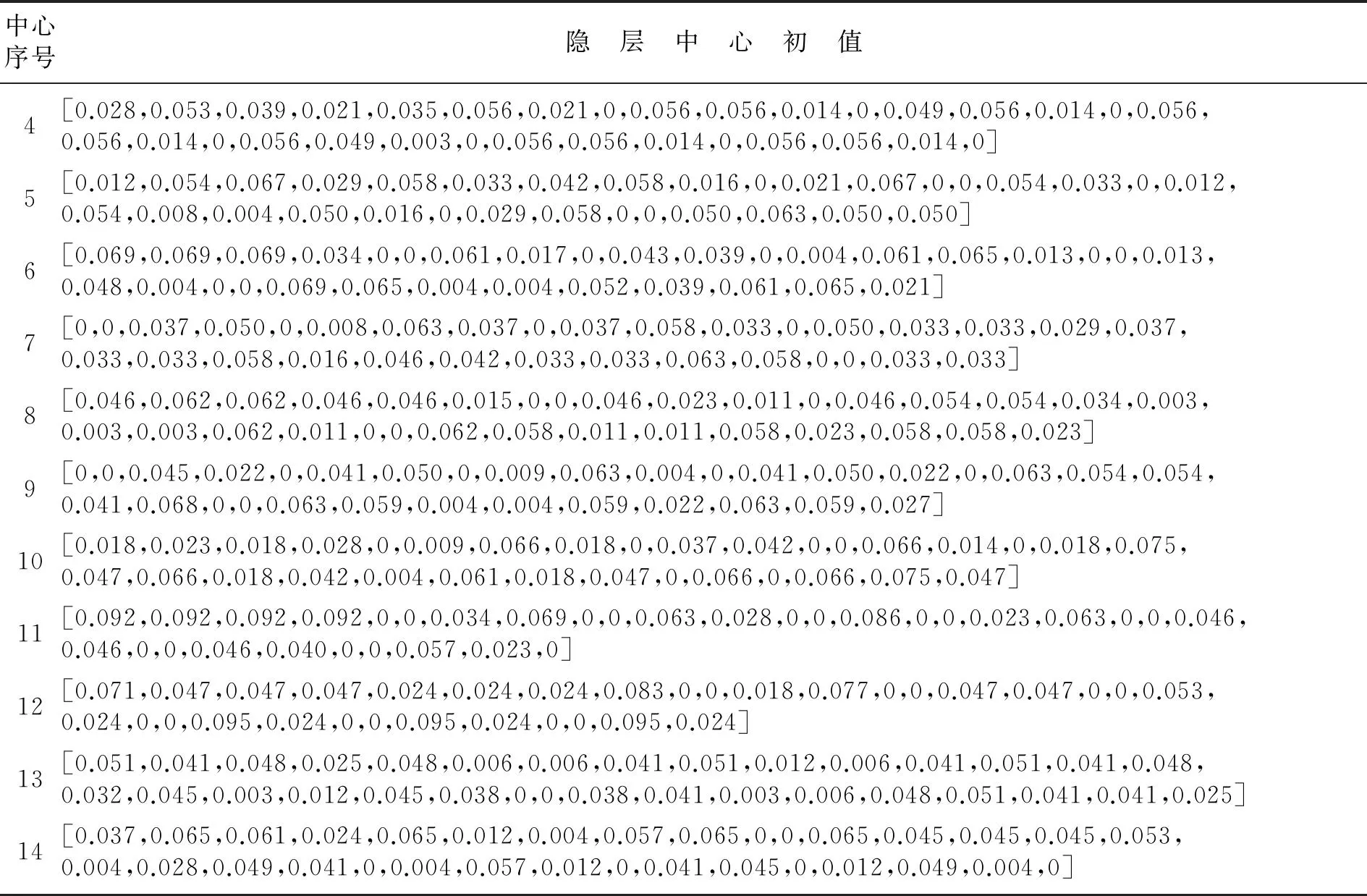
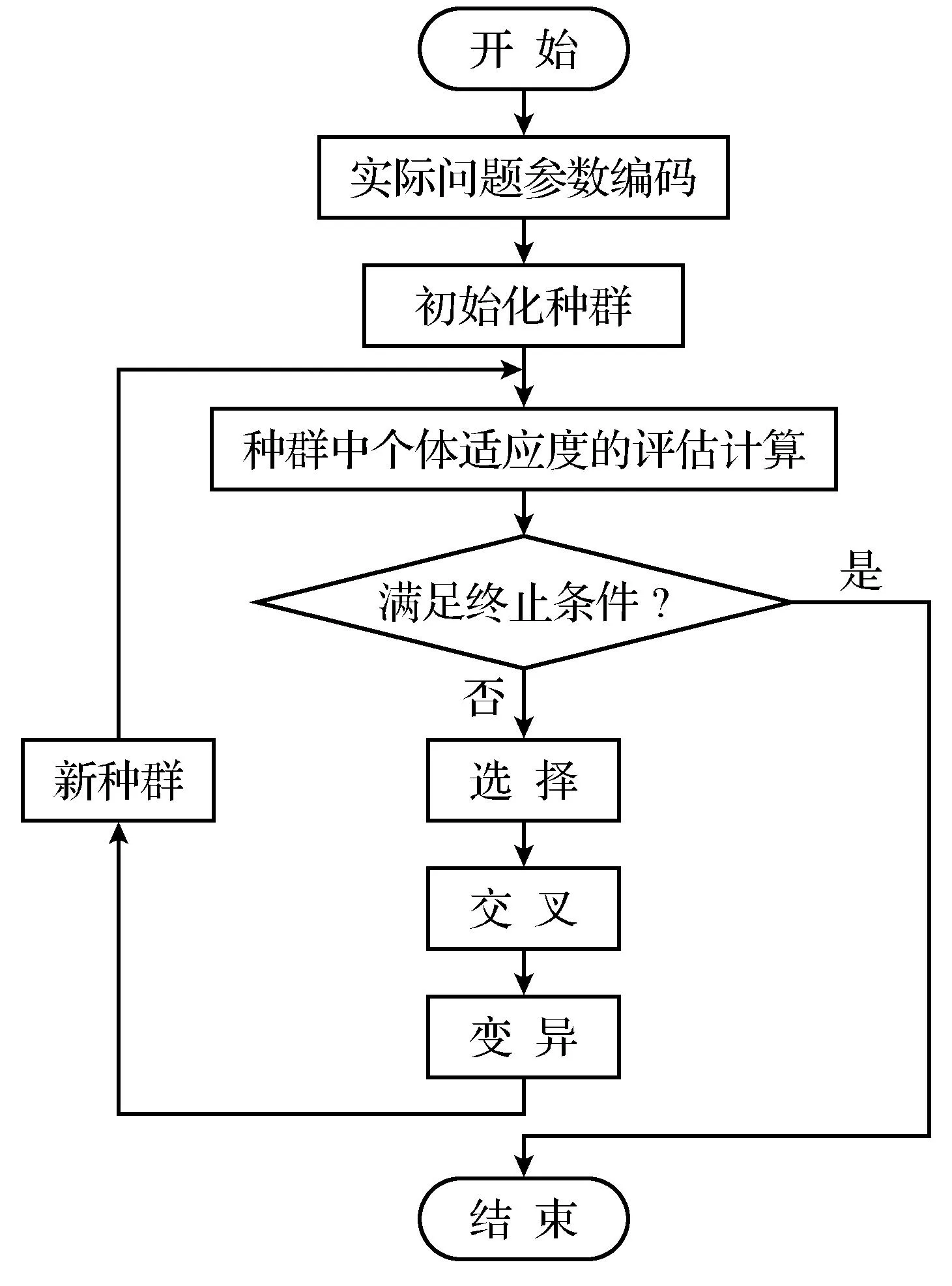
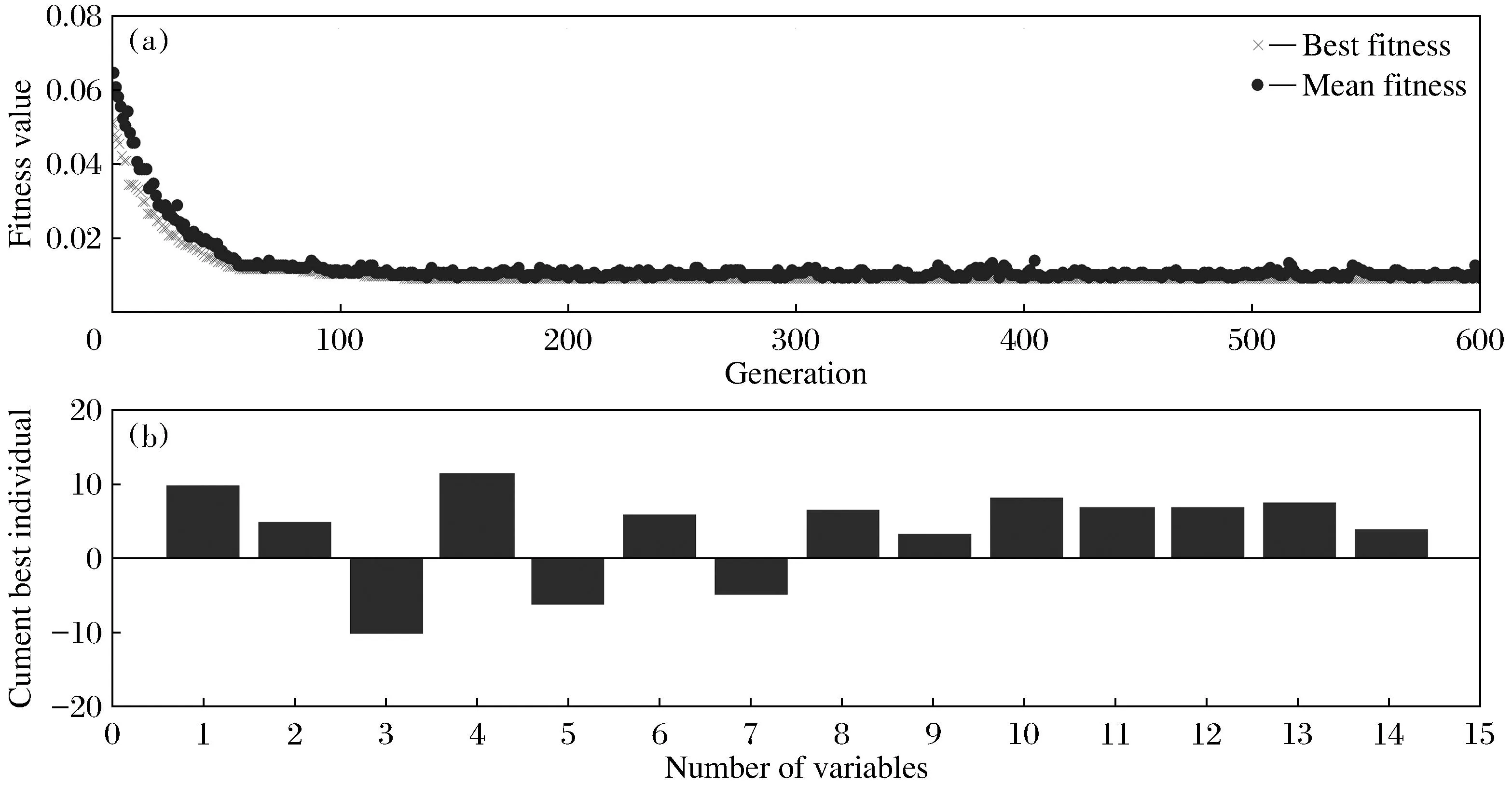
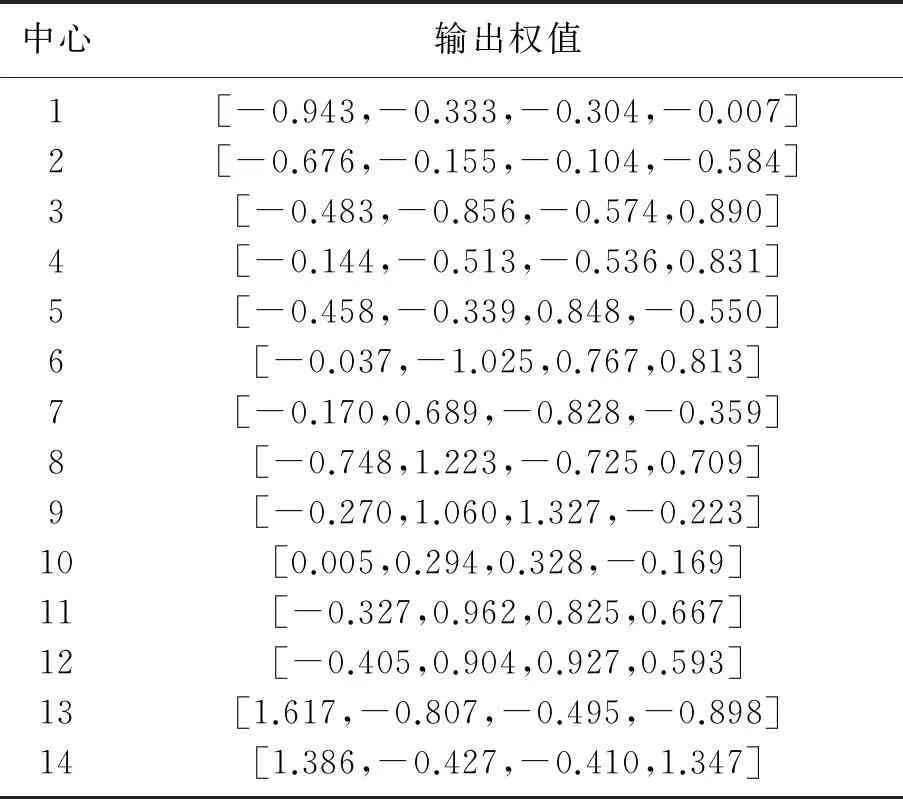
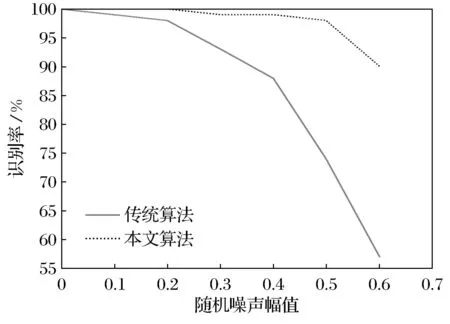
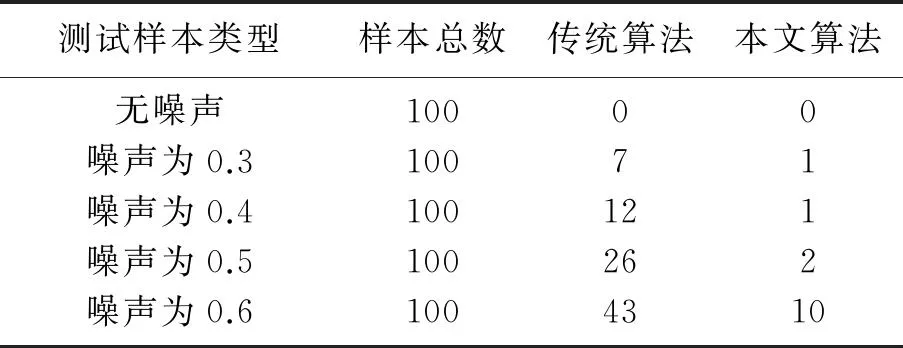
(3) 考虑第二个样本数据x2,并求出x2与第一个聚类中心x1的距离‖x2-x1‖,若‖x2-x1‖ (4) 假设考虑第k个样本数据xk时,k=3,4,…,已存在m个初始聚类中心c(1),c(2),…,c(m),在分别求出其与各聚类中心的距离ρ=‖xk-c(i)‖后,从中选取最小值ρmin,若ρmin>r,则将其作为一个新的聚类中心,否则聚类中心保持不变; (5) 根据矢量c(i),得到初始聚类中心及个数. 针对本文所采用的50个训练数据,将宽度r选择为0.1,得到了14个初始聚类中心,其值如表1所示. 表1 隐层中心初值 续表1 中心序号隐 层 中 心 初 值4[0.028,0.053,0.039,0.021,0.035,0.056,0.021,0,0.056,0.056,0.014,0,0.049,0.056,0.014,0,0.056,0.056,0.014,0,0.056,0.049,0.003,0,0.056,0.056,0.014,0,0.056,0.056,0.014,0]5[0.012,0.054,0.067,0.029,0.058,0.033,0.042,0.058,0.016,0,0.021,0.067,0,0,0.054,0.033,0,0.012,0.054,0.008,0.004,0.050,0.016,0,0.029,0.058,0,0,0.050,0.063,0.050,0.050]6[0.069,0.069,0.069,0.034,0,0,0.061,0.017,0,0.043,0.039,0,0.004,0.061,0.065,0.013,0,0,0.013,0.048,0.004,0,0,0.069,0.065,0.004,0.004,0.052,0.039,0.061,0.065,0.021]7[0,0,0.037,0.050,0,0.008,0.063,0.037,0,0.037,0.058,0.033,0,0.050,0.033,0.033,0.029,0.037,0.033,0.033,0.058,0.016,0.046,0.042,0.033,0.033,0.063,0.058,0,0,0.033,0.033]8[0.046,0.062,0.062,0.046,0.046,0.015,0,0,0.046,0.023,0.011,0,0.046,0.054,0.054,0.034,0.003,0.003,0.003,0.062,0.011,0,0,0.062,0.058,0.011,0.011,0.058,0.023,0.058,0.058,0.023]9[0,0,0.045,0.022,0,0.041,0.050,0,0.009,0.063,0.004,0,0.041,0.050,0.022,0,0.063,0.054,0.054,0.041,0.068,0,0,0.063,0.059,0.004,0.004,0.059,0.022,0.063,0.059,0.027]10[0.018,0.023,0.018,0.028,0,0.009,0.066,0.018,0,0.037,0.042,0,0,0.066,0.014,0,0.018,0.075,0.047,0.066,0.018,0.042,0.004,0.061,0.018,0.047,0,0.066,0,0.066,0.075,0.047]11[0.092,0.092,0.092,0.092,0,0,0.034,0.069,0,0,0.063,0.028,0,0,0.086,0,0,0.023,0.063,0,0,0.046,0.046,0,0,0.046,0.040,0,0,0.057,0.023,0]12[0.071,0.047,0.047,0.047,0.024,0.024,0.024,0.083,0,0,0.018,0.077,0,0,0.047,0.047,0,0,0.053,0.024,0,0,0.095,0.024,0,0,0.095,0.024,0,0,0.095,0.024]13[0.051,0.041,0.048,0.025,0.048,0.006,0.006,0.041,0.051,0.012,0.006,0.041,0.051,0.041,0.048,0.032,0.045,0.003,0.012,0.045,0.038,0,0,0.038,0.041,0.003,0.006,0.048,0.051,0.041,0.041,0.025]14[0.037,0.065,0.061,0.024,0.065,0.012,0.004,0.057,0.065,0,0,0.065,0.045,0.045,0.045,0.053,0.004,0.028,0.049,0.041,0,0.004,0.057,0.012,0,0.041,0.045,0,0.012,0.049,0.004,0] 2.3k-均值聚类算法优化RBF神经网络中心 k-均值聚类算法是目前应用最广的基于划分的聚类算法[8],该算法以k为参数,把n个对象分成k个簇,使簇内具有较高的相似度,而簇间相似度较低.算法通常采用误差平方和函数为最优化的目标函数,使其达到最小为目标,如式(6)所示: 式中,k表示聚类的数目,c(i)表示聚类中心值(i=1,2,…,k),x表示中心值为c(i)的簇的任一数据对象.显然e值越小,聚类效果就越好.与大多数聚类算法一样,k-均值聚类算法也有其自身的局限性:①聚类数目k值需要由用户事先确定;②算法严重依赖于初始中心值的选取,初始聚类中心选取不当容易导致错误的聚类结果. 针对以上不足,本文采用之前通过最近邻聚类算法得到的聚类簇数及聚类中心值来初始化参数k以及初始聚类中心值,改进的k-均值聚类算法步骤如下: (1) 对样本数据应用最近邻聚类算法得到聚类数k及初始聚类中心值; (2) 分别计算数据集中每个数据对象到各个聚类中心的距离(通常采用欧式距离),根据最近邻原则将数据对象逐个划分到离其最近的聚类中心所代表的簇中,根据式(6)计算误差平方和e; (3) 更新聚类中心,即分别计算各个簇中所有数据对象的均值,并将其作为各个簇新的中心,以新的聚类中心再次计算误差平方和e; (4) 将步骤3中计算的误差平方和e和前一次计算得到的e值进行比较,若两者差值的绝对值小于预先设定的阈值,则聚类准则函数(6)接近收敛,转至步骤(5),否则转至步骤(2); (5) 输出k个聚类中心值. 这样就可以使得最后的聚类结果具有较好的准确性,并将最后的聚类结果作为神经网络的中心,其值如表2所示 表2 隐层中心最终值 续表2 中心序号隐 层 中 心 初 值3[0.023,0.040,0.040,0.022,0.022,0.040,0.040,0.021,0.026,0.040,0.040,0.022,0.024,0.040,0.040,0.024,0.022,0.040,0.040,0.021,0.022,0.040,0.040,0.021,0.022,0.038,0.040,0.020,0.019,0.035,0.040,0.026]4[0.028,0.053,0.039,0.021,0.035,0.056,0.021,0,0.056,0.056,0.014,0,0.049,0.056,0.014,0,0.056,0.056,0.014,0,0.056,0.049,0.003,0,0.056,0.056,0.014,0,0.056,0.056,0.014,0]5[0.017,0.061,0.066,0.032,0.046,0.023,0.020,0.062,0.007,0,0.011,0.065,0,0,0.051,0.033,0,0.019,0.054,0.003,0.006,0.059,0.010,0,0.044,0.047,0.006,0.005,0.059,0.066,0.061,0.057]6[0.058,0.064,0.066,0.048,0,0.001,0.055,0.025,0,0.042,0.046,0,0.002,0.051,0.060,0.026,0,0,0.006,0.057,0.008,0,0,0.064,0.064,0.005,0.009,0.058,0.030,0.061,0.063,0.020]7[0.004,0.003,0.035,0.035,0,0.007,0.062,0.033,0,0.036,0.061,0.033,0.001,0.051,0.035,0.032,0.026,0.039,0.031,0.034,0.055,0.022,0.040,0.042,0.045,0.047,0.060,0.059,0,0,0.026,0.033]8[0.051,0.059,0.059,0.048,0.050,0.013,0,0,0.052,0.021,0.012,0.001,0.049,0.055,0.053,0.037,0.004,0.004,0.003,0.058,0.007,0,0,0.055,0.058,0.007,0.006,0.057,0.027,0.060,0.058,0.025]9[0,0.005,0.050,0.020,0,0.040,0.039,0,0.012,0.057,0.004,0,0.039,0.052,0.030,0.003,0.058,0.049,0.040,0.048,0.068,0.004,0,0.062,0.059,0.011,0.012,0.060,0.018,0.063,0.062,0.023]10[0.018,0.023,0.018,0.028,0,0.009,0.066,0.018,0,0.037,0.042,0,0,0.066,0.014,0,0.018,0.075,0.047,0.066,0.018,0.042,0.004,0.061,0.018,0.047,0,0.066,0,0.066,0.075,0.047]11[0.080,0.085,0.085,0.091,0.004,0.004,0.034,0.071,0,0,0.063,0.033,0,0.003,0.083,0.004,0,0.021,0.070,0,0,0.037,0.053,0,0,0.042,0.046,0,0,0.049,0.031,0]12[0.075,0.059,0.059,0.059,0.016,0.016,0.017,0.081,0,0,0.022,0.070,0,0,0.050,0.044,0,0.001,0.060,0.022,0,0.006,0.091,0.016,0,0.006,0.091,0.016,0,0.006,0.091,0.016]13[0.026,0.049,0.051,0.022,0.044,0.011,0.008,0.045,0.045,0.009,0.007,0.045,0.036,0.046,0.050,0.028,0.042,0.018,0.019,0.043,0.046,0,0,0.044,0.046,0.005,0.009,0.047,0.031,0.049,0.048,0.017]14[0.025,0.063,0.062,0.023,0.061,0.011,0.006,0.059,0.066,0.001,0.001,0.066,0.043,0.047,0.047,0.058,0.002,0.025,0.046,0.045,0,0.002,0.054,0.020,0,0.034,0.048,0.004,0.009,0.046,0.006,0.05] 2.4伪逆法与遗传算法结合确定网络中心宽度和输出权值 在图5所示的RBF神经网络拓扑图中,假设输入数据集合中含有l个输入向量,输入层节点个数为n个,隐层中心个数为m个且隐层中心值和中心宽度已经确定,输出层节点个数为p个,则隐层输出矩阵为H=(hij)l×m,其中hij表示第i个输入向量对应的第j个隐节点的输出;隐层到输出层的权值 矩阵为W=(wst)m×p,其中wst表示第s个隐节点到第t个输出节点的输出权值,标准输出矩阵为D.由此可得: 综上所述,只要确定了隐层中心值与中心宽度,那么权值即可通过伪逆法求得. 本文通过遗传算法[9]求取中心宽度.遗传算法借鉴了达尔文的进化论和孟德尔的遗传学说,其本质是一种高效、并行、全局搜索的方法,在求解具体问题时,遗传算法首先要求构建一个初始群体,群体中的任一个体均是原问题的一个可行解的编码,从而整个初始群体构成问题解集的一个随机采样,然后引入适应度函数作为优胜劣汰的依据来评价群体中个体的优劣程度,随后通过引入遗传学中交叉、变异的概念,对选出的优胜个体进行交叉、变异操作生成新的个体,最后根据一定的选择策略生成下一代种群,如此反复迭代,直到得到满意结果为止.遗传算法优化流程如图6所示. 图6 遗传算法流程图 本文利用遗传算法工具箱[10]对14个中心宽度进行优化,在MATLAB命令窗口中输入gatool即可打开遗传算法工具箱GUI界面.其运行参数设定如下:将变量个数取为14,将generations(代数)、stallgenerations(停滞代数)设为inf,在Plotfunction窗口中选择Bestfitness和Bestindividual,其余参数取为默认值.由于隐层中心值、标准输出已经确定,在将14个中心宽度设定为未知量后,可以根据式(8)、式(9)表示出输出权值,根据公式(5)求得网络实际输出.基于上述原理,将均方误差作为因变量,将14个未知的中心宽度作为自变量编写适应度函数. 运行遗传算法,在其达到600多代时适应度函数达到最小值,其值约为8.6767×10-3,适应度函数曲线及最优个体如图7所示,最终由遗传算法得中心宽度为 图7 GA优化过程及优化结果 在中心宽度确定后,由式(8)、式(9)可得输出权值,其值如表3所示. 表3 神经网络输出权值 在对数字识别的实验中,本文从100张(每个数字均为10张)数字图片中选取50张(每个数字对应5张)作为网络的训练样本.神经网络的输入层节点个数为32个(由输入向量维数决定),隐层节点个数为14个,在对标准输出进行编码时,采用8421BCD码代表相应的十进制数字,如0的编码为(0,0,0,0),9的编码为(1,0,0,1),故输出层节点个数取为4个.由于经过RBF神经网络得到的输出并不能保证是由0、1组成的向量,所以本文首先求得网络输出与各标准输出之间的最小误差,然后认为与该最小误差相对应的标准输出就是实际输出,即识别结果. 本文以传统的基于中心自组织学习算法(其中中心值与本文的相同,中心宽度采用公式(1)求得,权值通过最小二乘法求得)和上文中的混合学习算法分别训练网络,并用无噪声的全部样本以及分别添加0.3、0.4、0.5、0.6的随机噪声而生成的新样本对设计的网络分别进行测试.测试样本与识别结果误差曲线分别如图8、图9所示,图9中样本序列号代表样本编号,1~10表示数字0,依次类推,为了便于观察,本文将离散的识别结果误差用曲线连接起来,从图9中可以看出,在随机噪声为0.4时,用本文提出的算法只误识了1个字符,而传统算法误识别的字符则高达12个. 为了更好地说明此混合算法的识别能力,图10给出了识别率曲线,表4是字符识别错误个数统计. 图8 数字测试样本 图10 字符识别率 测试样本类型样本总数传统算法本文算法无噪声10000噪声为0.310071噪声为0.4100121噪声为0.5100262噪声为0.61004310 从以上结果可以看出本文所设计的神经网络在用未添加噪声的50个样本进行训练后,用全部样本及添加了噪声的样本进行测试,当噪声小于0.5时,识别率在98%以上,当噪声达到0.6时,识别率仍能达到90%,说明本文设计的RBF神经网络识别能力强,具有较好的抗干扰能力. 本文提出了将最近邻聚类算法、k-均值聚类算法、遗传算法和伪逆法结合确定RBF神经网络参数的方法.用最近邻聚类算法与k-均值聚类算法相结合的方法确定隐层中心值,使得聚类结果具有较好的客观性、准确性;将遗传算法与伪逆法应用到隐层中心宽度与输出权值的确定中,使参数达到全局最优.与基于梯度下降的误差纠正优化算法相比,该算法省去了对误差求导等运算,过程简单,计算量小,仿真结果证明了该算法的有效性. 参考文献: [1]李雪梅. 脱机手写体数字识别器的研究[J]. 沈阳大学学报, 1998(4):59-68. (LiXuemei.AStudyofOff-lineHandwrittenNumeralsRecognition[J].JournalofShenyangUniversity,1998(4):59-68.) [2]穆云峰.RBF神经网络学习算法在模式分类中的应用研究[D]. 大连:大连理工大学, 2006:10-11. (MuYunfeng.StudyontheApplicationofRBFNeutralNetworkLearningAlgorithmforPatternClassification[D].Dalian:DalianUniversityofTechnology, 2006:10-11.) [3]李国友,姚磊,李惠光,等. 基于优化的RBF神经网络模式识别新方法[J]. 系统仿真学报, 2006,18(1):181-184. (LiGuoyou,YaoLei,LiHuiguang,etal.ANewMethodofPatternRecognitionBasedonOptimizedRBFNeuralNetworks[J].JournalofSystemSimulation, 2006,18(1):181-184.) [4]侯雪梅. 基于全监督算法RBF神经网络的语音识别[J]. 西安邮电学院学报, 2011,16(1):87-90. (HouXuemei.SpeechRecognitionBasedonRBFNeuralNetworkwithEntire-SupervisedAlgorithm[J].JournalofXi’anUniversityofPostsandTelecommunications, 2011,16(1):87-90.) [5]WangRM,SangN,HuangR,etal.LicensePlateDetectionUsingGradientInformationandCascadeDetectors[J].Optik-InternationalJournalforLightandElectronOptics, 2014,215(1):186-190. [6]王洋,曾雪琴,范剑英. 汽车牌照字符识别系统设计[J]. 哈尔滨理工大学学报, 2012,17(1):90-95. (WangYang,ZengXueqin,FanJianying.DesignofRecognitionSystemforLicensePlateCharacter[J].JournalofHarbinUniversityofScienceandTechnology, 2012,17(1):90-95) [7]朱明星,张德龙.RBF网络基函数中心选取算法的研究[J]. 安徽大学学报:自然科学版, 2000,24(1):72-78. (ZhuMingxing,ZhangDelong.StudyontheAlgorithmsofSelectingtheRadialBasisFunctionCenter[J].JournalofAnhuiUniversity:NaturalScience, 2000,24(1):72-78.) [8]王塞芳,戴芳,王万斌,等. 基于初始聚类中心优化的k-均值算法[J]. 计算机工程与科学, 2010,32(10):105-107. (WangSaifang,DaiFang,WangWanbin,etal.AK-MeansAlgorithmBasedontheOptimalInitialClusteringCenter[J].ComputerEngineering&Science, 2010,32(10):105-107.) [9]DingSF,XuL,SuCY,etal.AnOptimizingMethodofRBFNeuralNetworkBasedonGeneticAlgorithm[J].NeuralComputing&Applications, 2012,21(2):333-336. [10]雷英杰,张善文,李续武,等.MATLAB遗传算法 工具箱及应用[M]. 西安:西安电子科技大学出版社, 2005:146-170. 【责任编辑:李艳】 (LeiYingjie,ZhangShanwen,LiXuwu,etal.MATLABGAToolboxandApplication[M].Xi’an:Xi’anUniversityofElectronicScienceandTechnologyPress, 2005:146-170.) DigitalIdentificationofRBFNeutralNetworkBasedonStructureHybridOptimization Zhang Xiuling1,2, Fu Dong1,LiHaibin1,LaiYongjin1,WangZhenchen1 (1.KeyLaboratoryofIndustrialComputerControlEngineeringofHebeiProvince,YanshanUniversity,Qinhuangdao066004,China; 2.NationalEngineeringResearchCenterforEquipmentandTechnologyofColdStripRolling,Qinhuangdao066004,China) Abstract:The digital recognition is taken as the application background to construct RBF neural network. Firstly, the nearest neighbor clustering algorithm and k-means clustering algorithm are applied to determine RBF neural network hidden layer center’s number and value adaptively; then genetic algorithm and pseudo inverse method are combined to determine the hidden layer center’s width and output weight; finally, based on hybrid optimization and the network based on center self-organizing learning algorithm, the experiment is finished by using the neural network. Stimulation results show that the network has the advantages of good recognition ability and small calculation quantity, which is constructed by using hybrid learning algorithm without noise samples and noise samples to test network. Key words:RBFNN; clustering; genetic algorithm; digital identification 作者简介:张秀玲(1968-),女,山东章丘人,燕山大学教授,博士. 基金项目:国家自然科学基金资助项目(61007003). 收稿日期:2014-12-22 文章编号:2095-5456(2015)03-0214-08 中图分类号:TP183 文献标志码:A


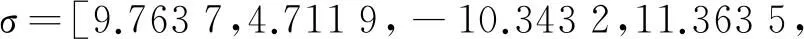
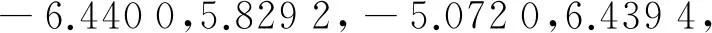
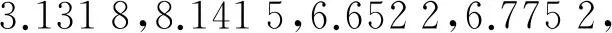
3 仿真实验及结果分析

4 结 论


