5 维Gauss－Bonnet－AdS 黑洞的热力学和临界现象

刘显明，雷焱林，陈 丽，韩 成

(湖北民族学院 理学院，湖北 恩施445000)

自从Bekenstein［1］和Hawking［2－4］建立起黑洞的热力学定律以来，国内外研究学者一直关注于对黑洞系统的热力学性质的研究． Davies 首先发现了在Kerr－Newman 黑洞系统存在热力学相变现象［5－6］．利用Landau－Lifshiz 的动力学涨落理论，研究者们进一步确认了在Ressner－Nordstrom 黑洞中存在二级相变现象，证明系统的热容量在相变点是发散的［7］．除此之外人们还利用热力学几何的方法对黑洞系统的热力学相变做了大量的研究［8］．

近年来，理论物理学家对渐进AdS 时空中黑洞的热力学性质的产生了浓厚的兴趣．Witten 指出一个AdS黑洞的热力学系统可以与一个高温强耦合的共形场对偶［9］．因此，研究AdS 黑洞热力学系统的性质可以洞察强耦合系统的热力学特征．这一思想也正是AdS/CFT 对应原理的具体体现．利用AdS/CFT 对应原理，理论物理学家近期建立了全息超导、超流、全息热化等理论模型，解释了强耦合系统的许多有趣的物理特征．最早研究发现AdS 黑洞的热力学系统存在Hawking－Page 相变［10］．近年来利用标准的热力学研究方法研究了大量的AdS 黑洞系统的热力学相变现象［11－14］．有趣的是，人们发现带电的AdS 黑洞系统的相变和临界行为与范德瓦耳斯物质的汽液相变非常类似．如果把宇宙学常数作为系统的压强，其共轭量作为系统的热力学体积V，黑洞系统P－V 相图正可以类比为一个范德瓦耳斯物质的P－V 相图．

本文将研究5 维Gauss－Bonnet－AdS 黑洞系统的热力学和临界现象．选取Bekenstein－Hawking 熵作为Gauss－Bonnet－AdS 黑洞的熵，讨论系统的相变现象，主要目的是讨论在存在高阶曲率项时AdS 黑洞系统是否存在相变现象、相变点的临界指数是否仍然满足热力学系统的普适热力学标度律．

1 5 维Gauss－Bonnet－AdS 黑洞的热力学

含有高阶的曲率项(Gauss－Bonnet 项)和宇宙学常数的5 维爱因斯坦引力的作用量为［15－16］:

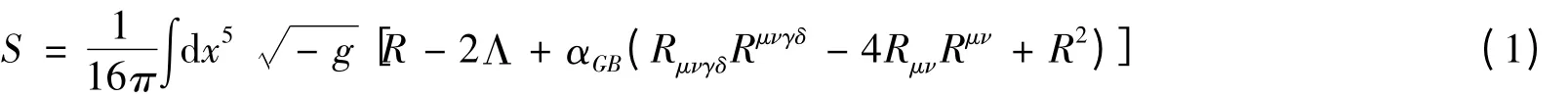
式中αGB是Gauss－Bonnet 系数，在低能弦论中要求αGB≥0，在文章中要求其也是非负的．通过变分可以得到引力场方程:

这比爱因斯坦场方程多出了高阶的曲率项．在该引力理论中存在类似于施瓦西黑洞的一类静态黑洞解，其线元为［17］:

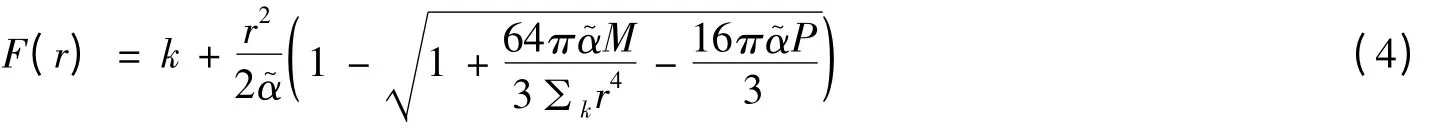
因此，由F(r+)=0 时，可以得到黑洞的质量:

黑洞的霍金温度可以计算得到为:

据此可以得到系统的基本热力学方程:

正如文献［18］指出，热力学熵仍然可近视选择为Bekenstein－Hawking 熵:

由此可以建立热力学．文献［18］基于此讨论了带电的Gauss－Bonnet－AdS 黑洞系统热力学相变现象，发现对于k=1 的球对称黑洞存在二级相变．本文同样基于Bekenstein－Hawking 熵，在P－V 相空间中，利用S≡SH来研究不带电的Gauss－Bonnet－AdS 黑洞的热力学相变现象．

根据式(5)、(6)、(8)和式(10)可以得到，热力学系统的焓:

和物态方程:

以及系统的其它热力学函数:

2 热力学相变及临界指数

接下来讨论系统的热力学相变并计算临界指数．首先，根据定义，可以得到系统的定压热容量CP．利用关系式:

代入式(10)、(12)可以得到:

由此结合式(12)可以求得对应的临界常数;

发现临界常数满足:

这是一个不依赖于Gauss－Bonnet 系数αGB的普适常数．这一结果与范德瓦尔斯系统非常类似．不同的是后者的临界系数是

类比于范德瓦尔斯系统，可以进一步计算黑洞系统在临界点的临界指数． 范德瓦尔斯系统的临界指数(α，β，γ，δ)可以根据以下定义求得:

5 维Gauss－Bonnet－AdS 系统中，根据式(8)、(10)，S仅仅是V的函数，因此可以得到:

所以α=0．

同时，在临界点引入

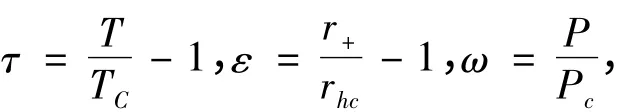
并假设ω 展开为下面的形式:

通过对τ、ε 在临界点求导数，可以容易得到系数:

于是(ω－1)|τ=0=－ε3，所以可得δ=3．

利用麦克斯韦等面积关系:

代入式(24)、(25)，可得:

另一方面，在相变点压强保持不变，即:

利用式(24)、(25)可得:

发生相变时要求T＜TC(τ ＜0)时，同一压强下有两个不同的体积，即εg≠εl，于是利用式(25)、(27)、(29)可以求得:

又因为:

所以可以求得γ=1．

因此，现在已经求得5 维Gauss－Bonnet－AdS 黑洞系统在临界点的临界指数这与范德瓦尔斯系统的临界指数是一样的．并且，很容易验证这些临界指数满足热力学系统的普适标度律:

3 结论

本文利用标准研究热力学系统相变的方法研究了一个5 维Gauss－Bonnet－AdS 黑洞系统的热力学及其相变现象．发现当采用Bekenstein－Hawking 熵作为系统的熵时，5 维的球对称Gauss－Bonnet－AdS 黑洞会发生相变，相变点的临界系数是一个与Gauss－Bonnet 系数无关的普适常数，并且临界指数与范德瓦尔斯系统一致且满足热力学普适标度律．结果证明了在扩展的P－V 相空间中，5 维Gauss－Bonnet－AdS 黑洞系统与范德瓦尔斯系统具有类似的热力学性质．

［1］ Bekenstein J D．Black Holes and Entropy［J］．Phys Rev D，1973，7:2333．

［2］ Hawking S W．Black hole explosions［J］．Nature，1974，248:30－31．

［3］ Hawking S W．Particle creation by black holes［J］．Commun Math Phys，1975，43:199－220．

［4］ Bardeen J M，Carter B，Hawking S W．The four laws of black hole mechanics［J］．Commun Math Phys，1973，31:161－170．

［5］ Davies P C W．The thermodynamic theory of black holes［J］．Proc R Soc London A，1977，353:499－521．

［6］ Davies P C W．Thermodynamic phasetransitions of Kerr－Newman black holes in de Sitter space［J］．Class Quantum Grav，1989，6:1909－1914．

［7］ Pav'on D．Phase transition in Reissner－Nordstrom black holes［J］．Phys Rev D，1991，43:2495－2497．

［8］ Quevedo H．Geometrothermodynamics of black holes［J］．Gen Rel Grav，2008，40:971－984．

［9］ Witten E．Anti de Sitter space and holography［J］．Adv Theor Math Phys，1998，2:253－291．

［10］ Hawking S W，Page D N．Thermodynamics of black holes in anti－deitter Space［J］．Commun Math Phys，1983，87:577－588．

［11］ Banerjee R，Modak S K，Samanta S．Glassy phase transition and stability in black holes［J］．Eur Phys J C，2010，70:317－328．

［12］ Banerjee R，Roychowdhury D．Thermodynamics of phase transition in higher dimensional AdS black holes［J］．JHEP，2011，11:004．

［13］ Banerjee R，Ghosh S，Roychowdhury D．New type of phase transitionin Reissner Nordstrom－AdS black hole and its hermodynamic geometry［J］．Phys Lett B，2011，696:156－162．

［14］ Banerjee R，Modak S K，Roychowdhury D．Thermodynamics of phasetransitions in AdS black holes［J］．JHEP，2012，10:125．

［15］ Kim H C，Cai R G．Slowly rotating charged Gauss－Bonnet black holes in AdS spaces［J］．Phys Rev D，2008，77:024045．

［16］ Cai R G．Gauss－Bonnet black holes in AdS spaces［J］．Phys Rev D，2002，65:084014．

［17］ Wiltshire D L．Black holes in string－generated gravity models［J］．Phys Rev D，1988，38:2445－2456．

［18］ Hu C，Zeng X X，Liu X M．Phase transition and critical phenomenon of AdS black holes in Einstein－Gauss－Bonnet gravity［J］．Sci China－Phys Mech Astron，2013，56(9):1652－1663．