煤矿突发事件应急救援的群决策方法*

陈孝国，母丽华，杜红，朱捷

(黑龙江科技大学理学院，黑龙江哈尔滨150022)

煤矿突发事件应急救援的群决策方法*

陈孝国，母丽华，杜红，朱捷

(黑龙江科技大学理学院，黑龙江哈尔滨150022)

提出了基于直觉模糊集的煤矿突发事件应急救援TOPSIS群决策模型。其中决策者权重采用偏好值与群体平均偏好值的相似度计算，属性指标权重采用直觉模糊熵权法确定。通过直觉模糊加权集成运算将各决策矩阵进行合成得到综合决策矩阵，利用改进后的直觉模糊距离公式计算出全部备选救援方案到正负理想解的距离，根据TOPSIS运算结果可以确定最佳事故救援决策方案。最后通过黑龙江省鸡西某矿的实例分析，验证了该模型的有效性及合理性。

应急救援;突发事件;群决策;直觉模糊集;熵

我国是世界上煤炭生产和消费大国，近几年产量均高达30亿t以上，有力支持和保障了国家经济建设快速发展的需要。但是，在煤炭高产背后，我们也付出了沉痛的代价，煤炭百万吨的死亡率达6人，是世界平均数的12倍，每年死于煤矿事故约有6 000人［1］。国家相继出台了一系列政策，使得重特大煤矿事故有所减少，但是整体安全形势仍然不容乐观。为了有效降低经济损失和减少人员伤亡，除了加强煤矿安全基础投入，防患于未然，还要建立健全煤矿事故应急救援响应机制，特别是应急决策，煤矿事故应急决策是一项复杂的、动态的、多阶段的过程，需要在全面分析的基础上快速确定最优方案，使得人员伤亡和经济损失降到最低。应急通讯［2］、应急预案［3-4］、应急信息管理系统［5-6］以及应急决策近年来成为国内为许多学者关注的热点，特别是在应急决策方面取得了一系列的理论成果。焦宇等［7］提出利用权变理论对煤矿瓦斯爆炸事故应急救援决策进行研究。王亮等［8］在全面考虑突发事件特点的基础上，提出动态决策参考点的概念并在权重已知的前提下借助前景理论对方案进行决策。靖可等［9］指出了煤矿事故应急救援中采用对称距离的不足之处，并在此基础上提出采用整体优势度实现备选方案与理想方案间的距离识别和最优决策，其中属性权重采用模糊层次分析法确定。肖全兴等［10］对煤矿灾害事故的特点进行了详细的分析，韩晋平等［11］在此基础上提出了煤矿事故应急救援综合能力的模糊评价方法。郭德勇等［12］提出要充分利用现有应急信息，建立煤矿应急辅助决策系统来提高应急救援决策的可行性。朗坤等［13］采用可变集理论对灾害应急物资合理分配进行了决策研究，属性权重根据模糊标度法计算。陈孝国等［14］建立了基于vague集的煤矿火灾救援路线优选决策模型，属性因素权重采用模糊层次分析法确定。

上述研究成果虽然在煤矿突发事件应急救援决策中能够提供理论支持，但是普遍存在决策可靠性不高和属性权重确定随意性较大的缺点和不足。基于此，本文提出了基于直觉模糊集的TOPSIS(technique for order preference by similarity to ideal solution)群决策方法。直觉模糊集比传统的模糊集描述问题更加细腻全面，已经在众多领域决策分析中取得了较好的效果。由多名专家进行的群决策能够使得决策结果更加可靠，属性权重采用直觉模糊熵权法来确定，避免了人为因素的影响，同时备选方案到正负理想解的距离采用改进后的直觉模糊加权距离，更加符合实际。最后通过黑龙江鸡西某矿瓦斯爆炸应急救援案例进行了决策分析。

1 相关理论

1.1 直觉模糊集理论

定义1［15］设X={x1，x2，…，xn}为论域。称A为X上一个直觉模糊集:

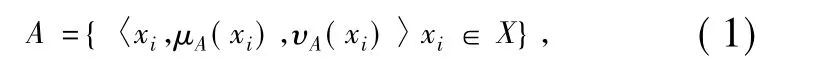
其中μA:X→［0，1］，υA:X→［0，1］，且0≤μA(xi)+ υA(xi)≤1，∀xi∈X。称μA(xi)和υA(xi)分别为xi∈A的隶属度和非隶属度。记πA(xi)=1-μA(xi)-υA(xi)为xi∈A的未知度，也称为犹豫度，且0≤πA(xi)≤1，xi∈X。通常称(μA(xi)，υA(xi)，πA(xi))为一直觉模糊数，简记(μA(xi)，υA(xi))。

对于任意两个直觉模糊集A和B均满足如下运算性质［15-16］:

为它们的距离。

定义3设ai=(μi，υi，πi)，i=1，2，…，n为一组直觉模糊数，则它们的直觉模糊加权集成运算为:

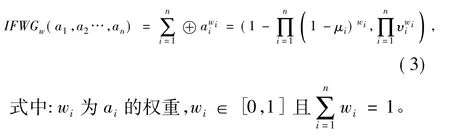
1.2 直觉模糊熵权理论

定义4［17］映射ESK:IFS(X)→［0，1］是一直觉模糊熵应该满足下述条件。

(1)ESK(A)当且仅当A为一脆集;

(2)ESK(A)=1当且仅当μA(xi)=υA(xi)，对于∀xi∈X;

(3)对于∀xi∈X，若μB(xi)≤υB(xi)，μA(xi)≤μB(xi)且υA(xi)≥υB(xi);或者μB(xi)≥υB(xi)，μA(xi)≥μB(xi)且υA(xi)≥υB(xi)，有ESK(A)≥ESK(B);

(4)ESK(A)=ESK(Ac)。

在满足上述公里化定义前提下，文献［17］中给出熵公式ESK(A)，文献［18］中给出熵公式EWL(A)，文献［19］中给出熵公式EHL(A)。

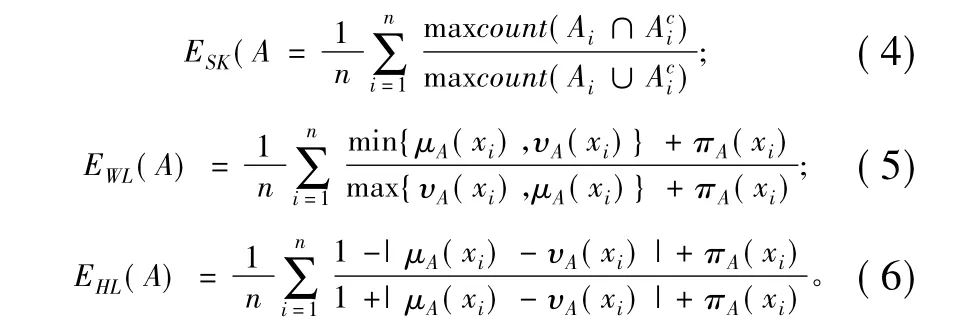
上述熵公式虽然在表达形式上有所不同，但实际上它们的值是相等的，ESK(A)=WWL(A)= EHL(A)，Wei等［20］已经证明了这一结论。

设方案集X={x1，x2，…，xm}，属性集Y={y1，y2，…，yn}，根据熵理论确定属性权重的方法通常是根据实际问题，在已知决策矩阵J的前提下，按照下述步骤进行求解。

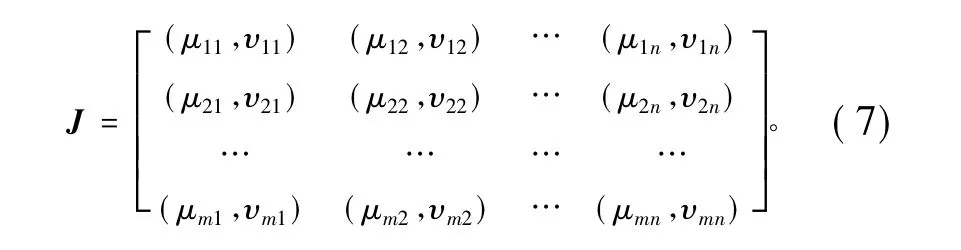
步骤1:利用满足定义4的熵度量计算出决策矩阵J中每个直觉模糊数所对应的熵值Eij。，得到矩阵T，

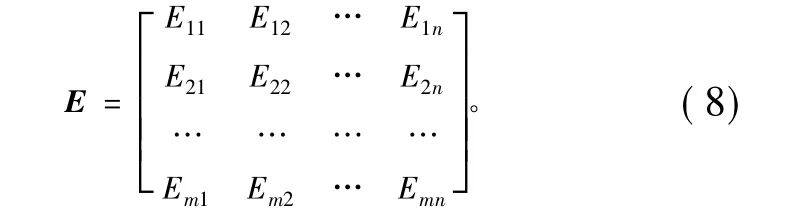
步骤2:对熵值进行规范化处理。

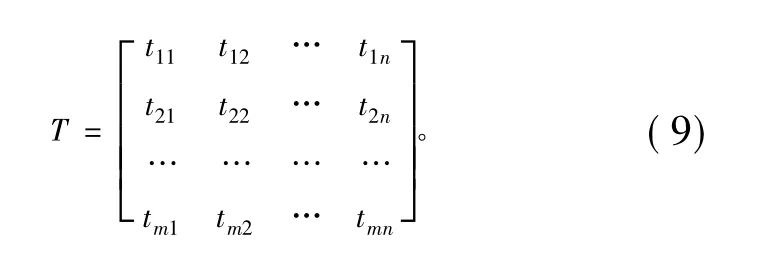
步骤3:属性权重求解。

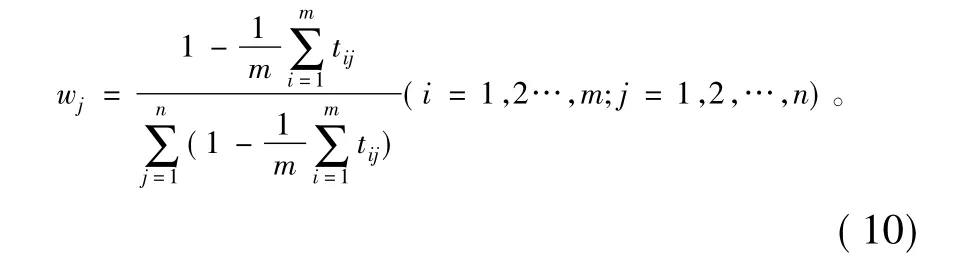
1.3 TOPSIS方法

Hwang和Yoon于1981年提出了TOPSIS(technique for order preference by similarity to ideal solution)方法［21］，它是在多目标决策问题中利用正理想解x+和负理想解x-对各个备选方案进行排序决策的方法。所谓正理想解x+是全部方案中所有属性最优值的一个组合，而负理想解x-是全部方案中所有属性最劣值的一个组合。TOPSIS的核心思想是将任意一个备选方案xi(i=1，2，…，m)与正负理想解的距离d(xi，x+)和d(xi，x-)进行对比，当备选方案xi与负理想解x-越远而与正理想解x+越近时方案越优。

设相对贴近度

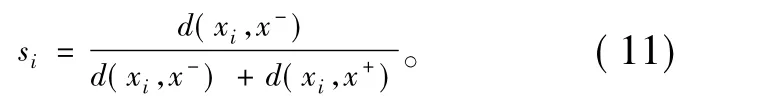
根据上述分析可以看出sj越大说明方案xi越优。

2 煤矿突发事件应急救援的TOPSIS群决策方法

(1)确定决策者权重。

在煤矿突发事件应急救援群决策中，当决策者的偏好信息越靠近群体的平均偏好值时，它具有的

在煤矿突发事件应急救援决策问题中，假设救援方案集X={x1，x2，…，xm}，m为救援方案的个数;救援决策属性集Y={y1，y2，…，yn}，n为属性个数;决策者集D={d1，d2，…，dl}，l为决策者个数，权重应该越大;相反则权重越大。设是决策者dk对方案xi关于属性yj的偏好值，群体对方案xi关于属性yj的偏好均值r*ij可由定义3求得(其中w1=w2之间的距离，用定义2计算。然后，计算r(k)ij与群体平均偏好的相似度

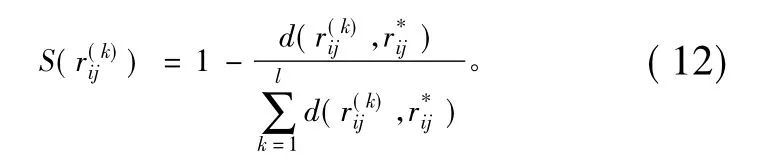
决策者dk的权重为:

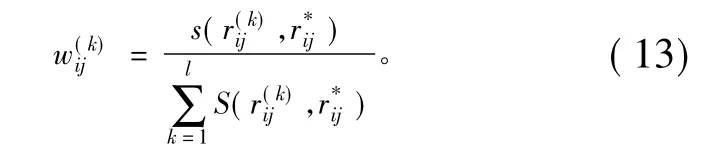
(2)将各评价矩阵进行集结运算。

将不同决策者dk给出的评价矩阵R(k)(k=1，2，…，l)进行集结，得到综合决策矩阵R=(rij)m×n，

(3)确定决策属性权重。

将综合决策矩阵R=(rij)m×n按照式(5)直觉模糊熵度量及1.2节中的权重确定方法计算各决策属性权重。

(4)确定正理想解和负理想解。

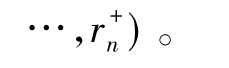
(5)各备选方案到正负理想解的加权距离求解。

设备选方案xi=(ri1，ri2，…，rin)，属性权重向量w=(w1，w2，…，wn)，则xi到正负理想解的距离分别为:

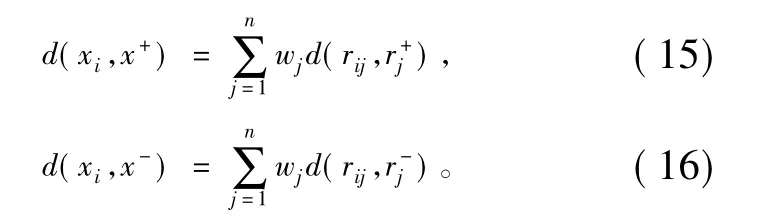
(6)决策分析。

根据式(11)计算各方案的相对贴近度si(i= 1，2，…，m)，按照取值大小进行排序，最大值对应的方案最优。

3 实例分析

黑龙江省鸡西某煤矿于某日早晨07:05听到井下有爆炸声，巷道烟雾较大，多处风井防爆门被摧毁，有黑烟冒出。经查四采区发生瓦斯爆炸，波及四采区下山至回风井所有区域，主要涉及325、326两个回采工作面系统和437掘进工作面系统，井下共有211名矿工，事故发生后，该矿立即启用应急救援响应机制，根据实际情况初步制定了4项应急救援方案xi(i=1，2，3，4)，为最大限度保障井下被困人员安全和降低经济损失，现聘请三位专家(决策者)dk(k=1，2，3)根据下面六项属性指标对救援方案进行评估，y1:灾区侦查和处理方法，y2:井下被困人员搜索方法，y3:恢复通风方法，y4:封闭及防止二次爆炸方法，y5:救灾人员的安全性，y6:救灾设备和资源搭配的合理性。采用直觉模糊数评价，构成三个评价矩阵R(1)、R(2)、R(3)，如下所示。

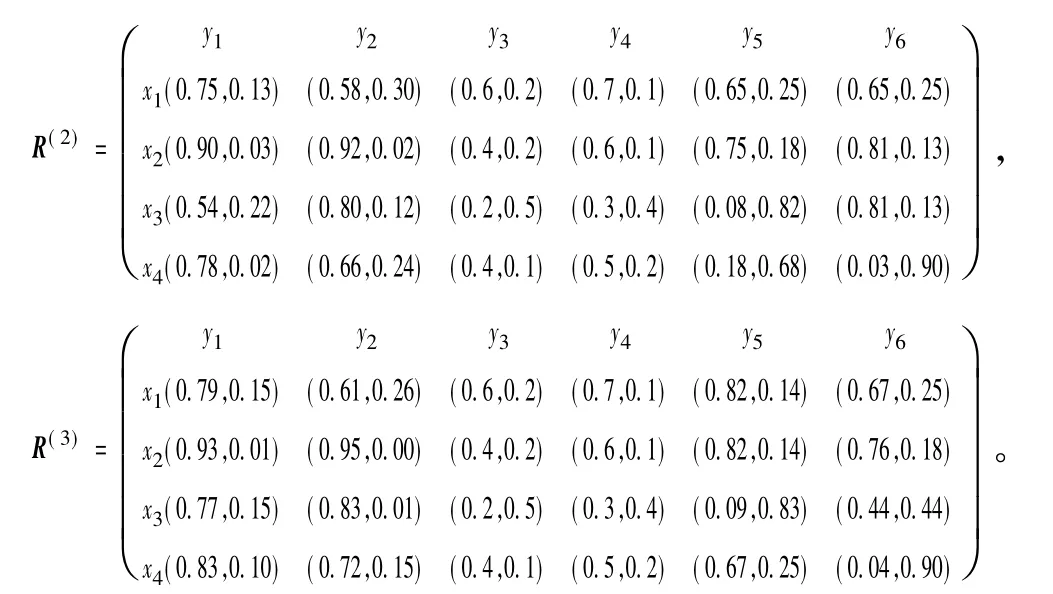
(1)对R(1)、R(2)、R(3)中偏好信息进行集结(其中得到平均偏好的矩阵R*，

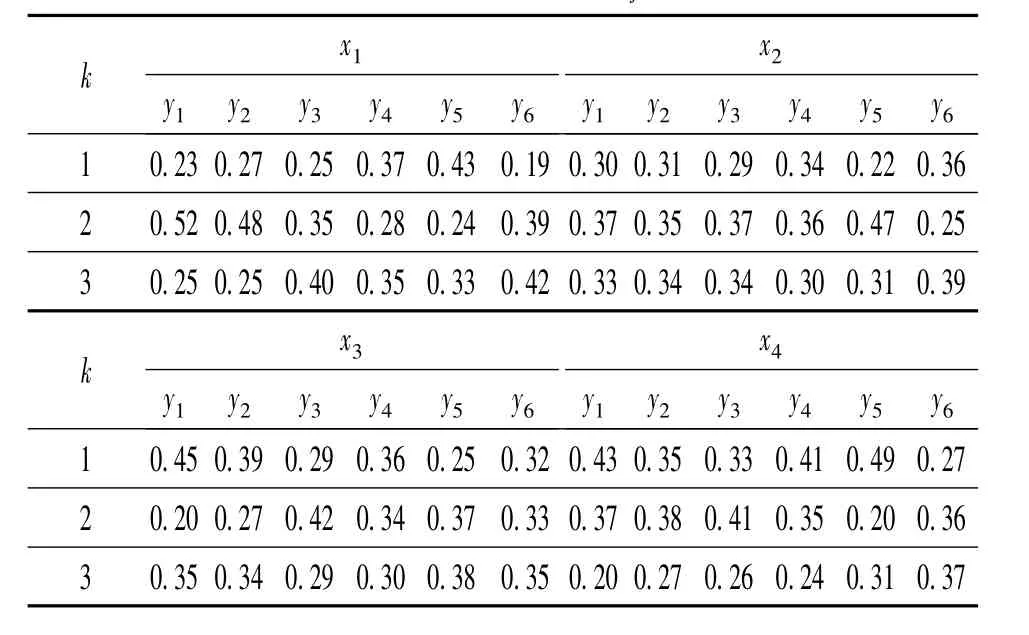
表1 决策者权重w(k)ij值

(2)将评价矩阵R(1)、R(2)、R(3)按相应专家权重集成为综合决策矩阵R。

(3)按照式(5)求出决策矩阵R对应的熵矩阵E。

根据1.2节中的权重确定方法计算得到决策属性权重W=(0.164，0.142，0.196，0.175，0.137，0.186)。

(4)上述决策属性类型均为效益型，所以

正理想解x+=((0.92，0.02)，(0.91，0.02)，(0.68，0.12)，(0.64，0.12)，(0.75，0.17)，(0.77，0.16))，

负理想解x-=((0.70，0.20)，(0.53，0.30)，(0.30，0.35)，(0.37，0.32)，(0.11，0.77)，(0.04，0.87))。

(5)按照式(15)和(16)求解x1到正负理想解的距离分别为:

d(x1，x+)=0.130 4，d(x2，x+)=0.068 8，d(x3，x+)=0.313 6，d(x4，x+)=0.292 3;

d(x1，x-)=0.336 0，d(x2，x-)=0.413 3，d(x3，x-)=0.208 7，d(x4，x-)=0.212 5。

(6)根据式(11)计算各方案的相对贴近度，s1=0.720 4，s2=0.857 3，s3=0.399 6，s4=0.420 9。最大值对应的应急救援方案x2最优。

4 结论

煤矿突发事件应急救援决策的关键是可靠性问题，在复杂多变的地质条件和众多不确定性因素的作用下，采用直觉模糊数来描述相关问题更加符合实际，而通过集成运算得到的TOPSIS群决策模型使得结果可靠性大幅提高，整个决策方法计算量较小，且易于编程求解。该项研究不仅丰富了煤矿应急救援决策的理论方法，同时也可以推广到其他领域。

［1］李卫.基于DCSP的煤矿应急救援资源调配研究［D］.重庆:西南大学，2011.

［2］王安义，杨柳.一种新的煤矿井下应急救援方案［J］.煤炭技术，2009，28(11):72-73.

［3］郭德勇，郑茂杰，程伟，等.煤与瓦斯突出事故应急预案研究与应用［J］.煤炭学报，2009，34(2):208-211.

［4］王铃丁，张瑞新，赵志刚，等.煤矿应急救援指挥与管理信息系统［J］.辽宁工程技术大学学报，2006，25(5):655 -657.

［5］Robot B，Kelly.Industrial emergency preparedness［M］.New York:Van Nostrand Reinhold，1991.

［6］张俊，许建华.突发事件应对中地方政府的处置原则研究［J］.灾害学，2014，29(1):182-187.

［7］焦宇，周心权，谭国庆.煤矿特别重大瓦斯爆炸事故应急救援及决策实施效果评价原则［J］.煤矿安全，2009，40(8): 116-119.

［8］王亮，王应明.基于前景理论的动态参考点应急决策方法研究［J］.中国管理科学，2013，21(11):132-140.

［9］靖可，赵希男.基于整体优势度的应急救援案例推理决策［J］.系统工程，2008，26(9):15-20.

［10］肖全兴，张涛.矿井灾害事故处理决策方法的研究［J］.煤炭科技，2001，12(2):49-51.

［11］韩晋平，毕永华，侯金玲，等.基于灰色-模糊综合法的煤矿应急救援能力评价研究［J］.西安科技大学学报，2011，31(2):146-152.

［12］郭德勇，刘金城，姜光杰.煤矿瓦斯爆炸事故应急救援响应机制［J］.煤炭学报，2006，31(6):697-670.

［13］朗坤，张明媛，袁永博.基于可变集的地震灾害应急物资分配模型［J］.灾害学，2014，29(1):201-206.

［14］陈孝国，杜红，母丽华，等.不确定条件下矿井火灾救灾路线优选的群决策方法［J］.中国安全科学学报，2014，24 (3):167-171.

［15］Atanassov K.Intuitionistic fuzzy sets［J］.Fuzzy Sets and Setsands，1986，20(1):87-96.

［16］De Luca A，Termini S.A definition of non probabilistic entropy in the setting of fuzzy theory［J］.Information and Control，1972，20 (4):301-312.

［17］Szmidt E，Kacprzyk J.Entropy for intuitionistic fuzzy sets［J］. Fuzzy Sets and Systems，2001，118(1):467-477.

［18］Wang Y，Lei Y J.A technique for constructing intuitionistic fuzzy entropy［J］.Control and Decision，2007，22(12):1390 -1394.

［19］Huang G S，Liu Y S.The fuzzy entropy of vague sets based on non -fuzzy sets［J］.Computer Applications and Software 2005，22 (6):16-17.

［20］Wei C P，Wang P，Zhang Y Z.Entropy，similaritymeasure of interval-valued intuitionistic fuzzy sets and their applications［J］. Information Sciences，2011，18(1):4273-4286.

［21］Hwang C L，Yoon K.Multiple Attributes Decision Making Methods and Applications［M］.Springer Berlin Heidelberg，1981:12 -23.

A Group Decision M aking M ethod of Coal M ine Emergency Rescue

Chen Xiaoguo，Mu Lihua，Du Hong and Zhu Jie
(School of Science，Heilongjiang University of Science and Technology，Harbin 150022，China)

A coalmine emergency rescuemodel of TOPSIS group decisionmaking is proposed based on intuitionistic fuzzy sets.The decisionmakersweights are calculated using similarity of preference value and the average preference，attribute index weight is determined with intuitionistic fuzzy entropy weightmethod.All decisionmatrices are synthesized to get the comprehensive decision matrix through integrated operation of weighted intuitionistic fuzzy numbers.All the distances between alternative rescue scheme and the positive and negative ideal solution are calculated by the improved intuitionistic fuzzy distance formulas.The optimal accident rescue decision scheme is got according to the results of TOPSISalgorithm.At last，a coalmine in Jixi City is taken as an example to analysis and prove the validity and rationality of themodel.

emergency rescue;emergency;group decision-making;intuitionistic fuzzy set;entropy

X924.4;X43

A

1000-811X(2015)01-0167-05

10.3969/j.issn.1000-811X.2015.01.031

陈孝国，母丽华，杜红，等.煤矿突发事件应急救援的群决策方法［J］.灾害学，2015，30(1):167-170.［Chen Xiaoguo，Mu Lihua，Du Hong，etal.A Group Decision Making Method of CoalMine Emergency Rescue［J］.Journal of Catastrophology，2015，30(1):167-170.］

2014-08-04

2014-09-25

国家自然科学基金项目(51105135);黑龙江省教育厅科学技术研究项目(12531577);黑龙江科技大学青年才俊资助项目(20120501)

陈孝国(1978-)，男，黑龙江克东人，副教授，主要从事模糊决策，煤矿安全方面研究.E-mail:kjdxcxg@sohu.com