海军战术导弹高海情条件下性能评估方法

黄济海

（92493部队装备部，葫芦岛125001）

海军战术导弹高海情条件下性能的评估，一般不会依赖于一种试验方式。例如，飞行试验可以全面检验高海情条件下武器系统性能，但由于试验条件的不可控性和导弹产品的高价值昂贵性，不可能进行多次试验，试验样本严重不足，只能是一次至两次的验证性试验，不具有统计特性，也不能据此完成性能评估，而必须依靠其它多类型试验获取足够多的试验信息，在此基础上完成高海情条件下的性能评估。

海军战术导弹高海情条件下的试验类型包括：模拟发射试验、导引头跟踪试验或挂飞试验（引信）、虚拟目标射击试验、飞行验证试验、仿真试验等。依靠这些试验获取的多种试验信息，通过信息综合完成战术导弹高海情条件下的性能评估。

事实上，利用多类型试验及其获取的多种形式的试验信息，通过信息综合实现高海情条件下导弹性能的置信估计或检验是困难的，主要原因是多源试验信息综合的复杂性和不确定性，致使信息综合不够准确，往往误差较大，评估结果的置信度较低。采用综合评价方法，可较好解决上述问题。综合评价方法可实现多源试验信息与综合评估的一体化处理，避免了试验信息综合与试验结果评估的隔离，试验信息利用充分，评估结果置信度相对较高。为此，本文拟采用基于层次分析法（AHP）和模糊综合评价方法进行战术导弹高海情试验结果评估。

1 海军战术导弹高海情性能评估指标体系的建立

高海情条件影响海军战术导弹性能主要有以下环节：

（1）发射环节：舰船摇摆情况下，导弹能否发射，导弹发射架调转精度、发射诸元装订精度等是否满足要求。

（2）飞行控制环节：在风、浪的影响下，导弹超低空弹道特性和飞行可靠性是否有所下降。

（3）导引头或目标跟踪传感器的跟踪环节：发现、捕获目标距离，跟踪稳定性和跟踪精度。

（4）制导与命中环节：导弹制导命中精度、引信工作性能、命中概率等均可能受到影响。

以反舰导弹为例，根据上述分析，分别确定高海情性能评估指标体系，如图1所示。

2 使用层次分析法确定各指标权重

2.1 构造判断矩阵

首先需确定AHP的比例标度，若采用5比例标度，对图1反舰导弹高海情性能评估指标构造判断矩阵。对图1中同一层次的各元素关于上一层次中某一准则的重要性，采用1～5标度进行两两比较，分别构造两两比较的判断矩阵 A、B1、B2、B3、B4。判断矩阵A如表1所示。

表1 判断矩阵A

同样，作为例子，若判断矩阵B2，如表2所示。其它判断矩阵同理可得。

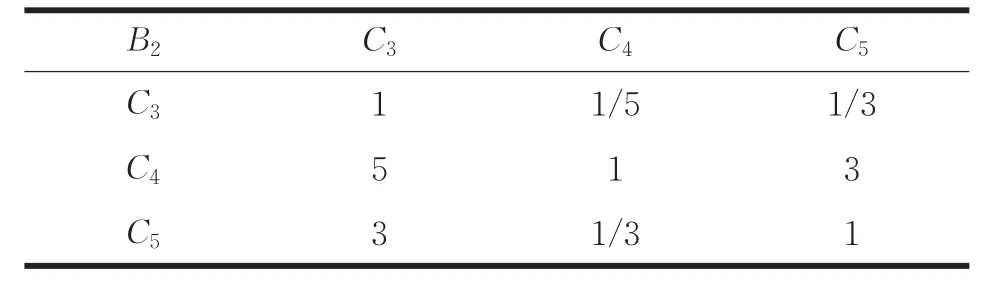
表2 判断矩阵B2

对于判断矩阵中两两比较的量化值，根据选用的标度，可通过专家打分或系统分析的方法确定。

2.2 计算各判断矩阵的特征向量和最大特征值

构造了满意的判断矩阵后，需要计算他的最大特征根及其对应的特征向量作为权重。在求判断矩阵A的特征根时，没有必要去精确计算最大特征根和特征向量，可以应用简便的计算方法。采用简便的方根法算法即可，计算步骤如下：

（1）计算判断矩阵A中每行所有元素的几何平均值

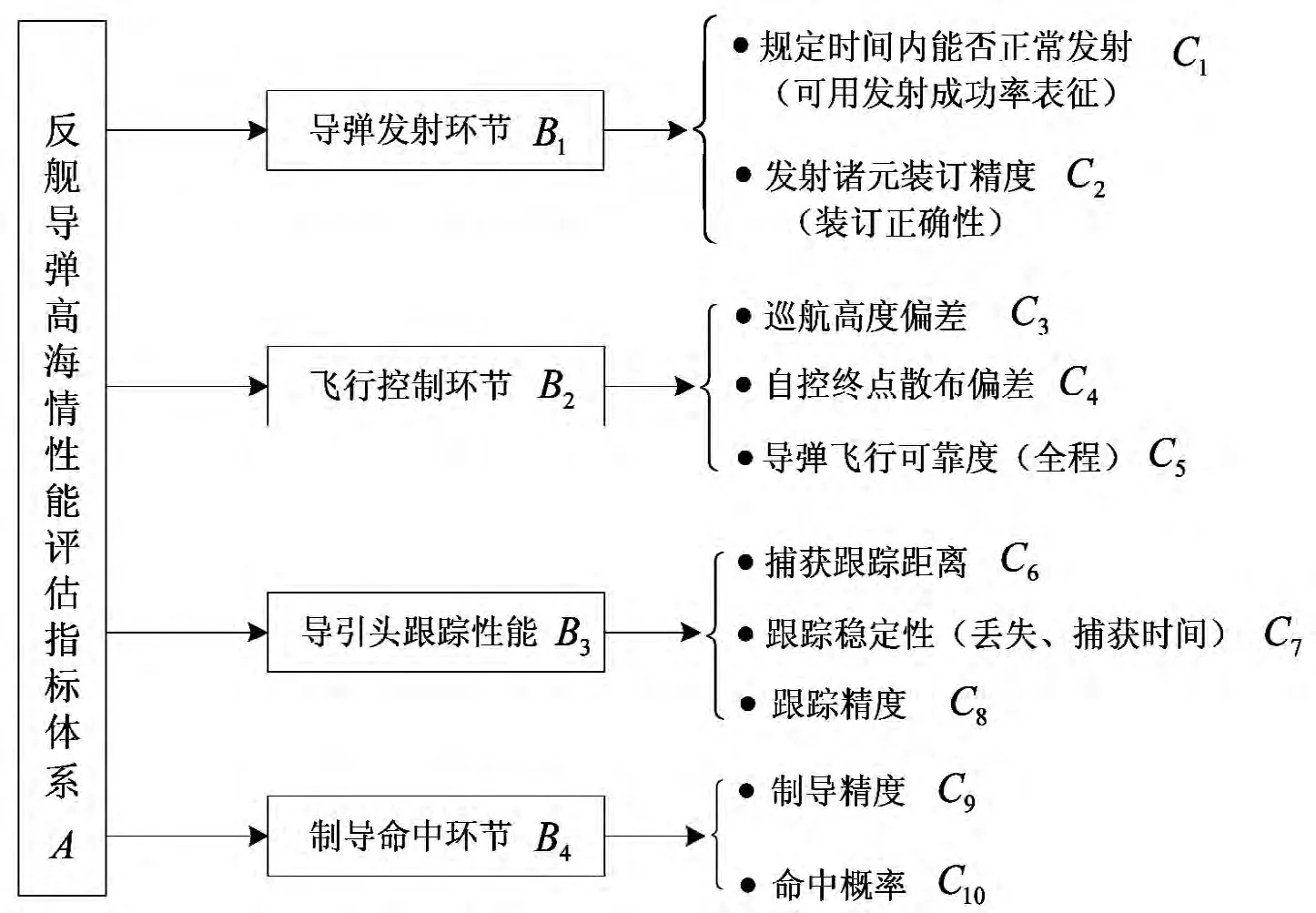
图1 反舰导弹高海情性能评估指标体系

得到W=(w1,w2,…,wn)T，即为所求特征向量的近似值，这也是各元素的相对权重。

在本例中：

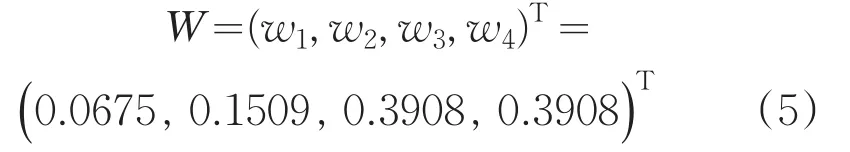
（3）计算判断矩阵的最大特征值λmax

判断矩阵的最大特征值的计算公式为

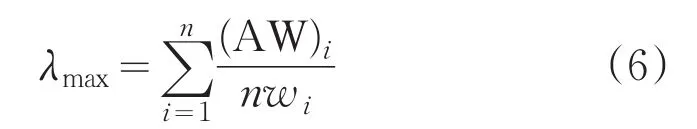
同样得到w2,w3,w4。于是得到

其中，( )AWi为向量AW的第i个元素。

在本例中：

则

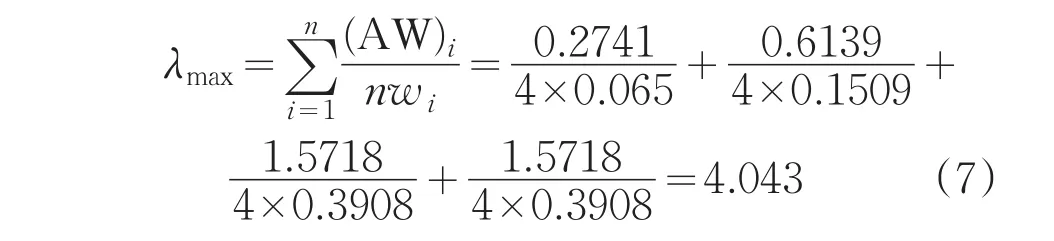
（4）利用上述同样的计算方法，可得到矩阵B1、B2、B3、B4的特征向量（即各元素相对权重）和最大特征值λmax。

最大特征值λmax用于判断矩阵进行一致性检验。一致性检验检验方法见文献［1］。至此，已经能够计算出评价指标体系中各指标的权重。

3 海军战术导弹高海情性能模糊评价方法

3.1 高海情性能模糊评价方法步骤

（1）确定反映战术导弹高海情性能的指标。例如图1，因素论域为：

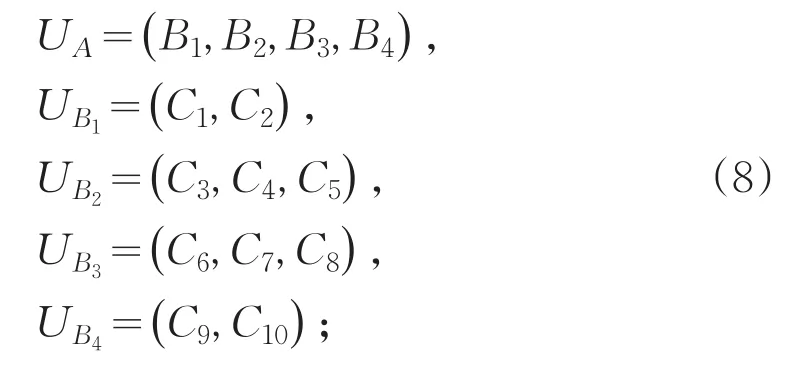
之后，再定义评价结果的等级论域定义为：

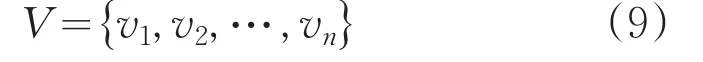
（2）确定评价指标的模糊关系矩阵

由于每项指标的含义不同，应根据具体试验结果、数据及相关资料或分析等，选择不同方法确定相应因素指标的模糊隶属度，得到相应的模糊关系矩阵 Ri。

例如，对图1的指标体系，若选用评价等级论域V={v1,v2,v3}={良好，合格，不合格}，则需确定如下模糊关系矩阵：

（3）确定评价指标权重

具体权重计算方法上面已明确，例如对图1的指标体系，计算得到如下权重：（4）应用模糊合成算子计算

同样以图1指标体系为例，计算得到模糊评语：

即

于是得到：

计算合成模糊评语有：

（5）评价

利用最大隶属度原则、加权平均方法或模糊向量数值化方法，对评价对象进行综合评价。

3.2 因素指标模糊隶属度的确定

根据上面叙述知道，战术导弹高海情性能评估的关键问题是评估指标模糊隶属度确定问题。由于每项指标的含义不同，确定隶属度的方法就会有差异，因此需分别讨论。确定隶属度的总的原则有两个方面，一是尽可能根据实际试验数据；二是采用指标对比法和比较法。比较法的含义是把高海情条件下的试验数据与非高海情条件下的试验数据进行比较来确定。具体确定方法可选择隶属度确定方法中的一种或几种来计算得到。

3.2.1 概率性指标隶属度计算方法

概率性指标包括发射成功率、引信虚警率、命中（杀伤）概率、飞行可靠度等。

（1）确定评价指标量化值

若V={v1,v2,v3}={良好，合格，不合格}，可按指标要求或非高海情条件下试验结果确定。如：V={良 好 ，合 格 ，不 合 格}={P1,P2,P3}，且P1＞P2＞P3；

（2）计算隶属度

若选用半梯形及梯形分布形式，偏大型。

若通过实际试验及统计，得到概率值P，则

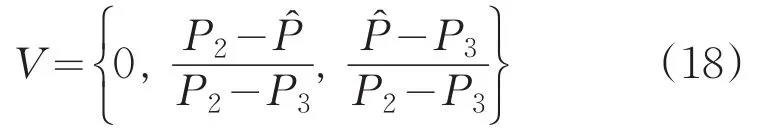
3.2.2 精度类指标隶属度计算方法

精度类指标包括发射诸元装订精度、发射架调转精度、传感器跟踪精度以及制导精度等。

（1）确定评价指标量化值

同样，若选取V={v1,v2,v3}={良好，合格，不合格}，精度指标量化有两种形式，一种是1σ原则，另一种是最大误差3σ原则。那么可选取V1={良好，合格，不合格}={σ,σ+20%σ,σ+50%σ}或V2={良好，合格，不合格}={σ,2σ,3σ}。

（2）计算隶属度

同样，选取半梯形及梯形分布形式的计算方法，偏小型。

通过实际试验及试验结果统计，得到某项精度

指标试验结果，则有

当 σ1＜o＜σ2时，

当 σ2≤ o＜ o3时，

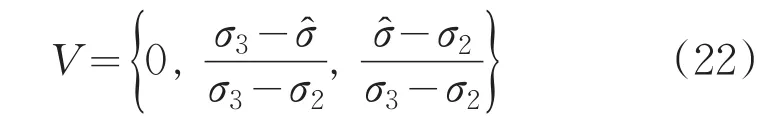
若选用V={σ,2σ,3σ}标准时，统计得到精度指标最大误差值Δmax，计算隶属度方法同上，这种方法更适合一次试验或样本较小的试验情况。

3.2.3 偏差类或数值类指标隶属度计算方法

该类指标主要包括系统反应时间、自控终点偏差、稳定跟踪距离等。其中，系统反应时间、自控终点散布指标属于偏小型，即试验结果数值越小，表明性能越优良；而稳定跟踪距离类指标属于偏大型指标，即试验结果数值越大，表明性能越好，在计算隶属度分布函数时要注意选择相应的计算表达式。

（1）选取评价指标量化值

可选取偏差类或数值类指标的指标值，或者非高海情试验结果的统计值为基准。例如，反舰导弹自控终点偏差指标在非高海情条件下（3级以下）试验统计值为R，则可选取：

（2）计算隶属度

同样，采用半梯形及梯形分布，偏小型计算公式，有

当R≤R1时，

当R1＜R＜R2时，

当R2≤R＜R3时，

当R≥R3时，

其它指标计算方法类似。

3.2.4 模糊类指标隶属度计算方法

该类指标主要包括跟踪稳定性、弹道性能、弹道关键特征点控制性能等。这类指标虽然没有确定的指标值，但根据具体武器系统的特点和实际试验结果，通过系统分析，可以确定其隶属度。

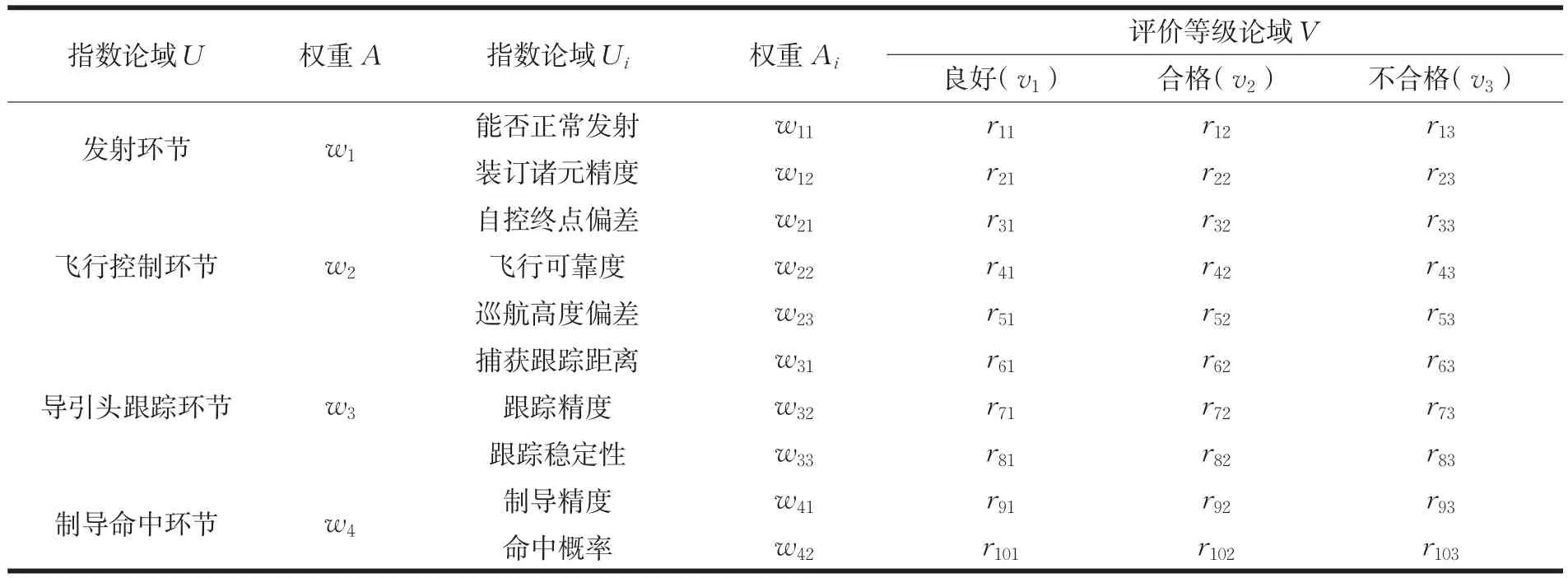
表3 海军战术导弹高海情性能评估结果数据表

例如，导引头或目标跟踪传感器跟踪稳定性指标，若选取V={良好，一般，差}或V={良好，合格，不合格}，可根据传感器丢失目标次数、距离、再捕获时间、时机等试验数据，分析或仿真其对导弹命中的影响程度，来确定隶属度。如通过没有影响、影响较小、影响较大等分析估论来确定其隶属度。

4 综合评估方法演示

以反舰导弹高海情性能评估为例，进行综合评估。对于如图1指标体系，通过确定各层次指标权重、确定各项指标模糊隶属度，得到如表3结果。

则有

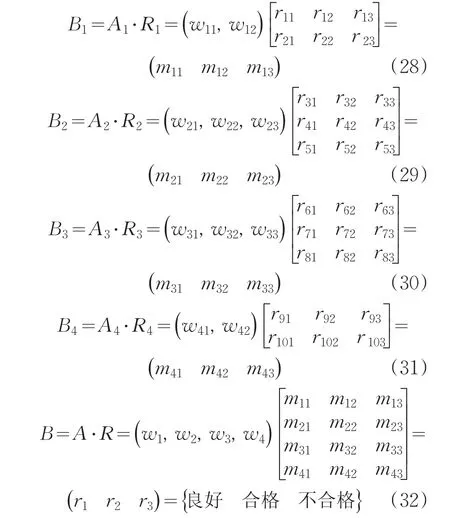
评价：

①最大隶属度评价原则法

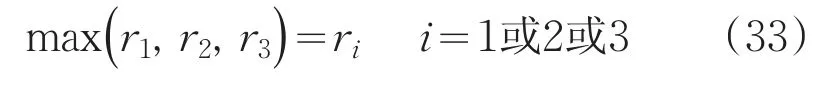
式中ri对应的良好或合格或不合格为评价结果。

②模糊向量数值化

若令良好v1=100，合格v2=70，不合格v3=50，应用公式可得

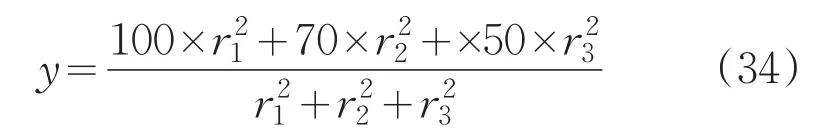
③加权平均法

若令良好v1=100，合格v2=70，不合格v3=50，应用公式可得

5 结语

海军战术导弹高海情条件下性能评估，一直是人们关注的重点和难点问题。本文提出的基于多种试验方式、将层次分析法和模糊评价法相结合的综合评估方法，具有合理、简便的特点，降低了人为因素的影响，可以使评估结果更为合理可靠，可操作性较强。另外，文中仅以反舰导弹为例，其思想方法可以推广到舰空导弹等其他战术导弹高海情试验与评估中。

［1］冯璐，高晓光.层次分析法在多目标攻击逻辑与决策中的应用［J］.西北工业大学学报，1999，17（4）：516-518.

［2］张最良，李长生，赵文志，等.军事运筹学［M］.北京：军事科学出版社，1997：377-381.

［3］魏继才，黄谦，胡晓峰.层次分析法在武器系统效能建模中的应用［J］.火力与指挥控制，2002，27（3）：24-26.

［4］曲宝忠，孙晓峰.海军战术导弹试验与鉴定［M］.北京：国防工业出版社，2006.

［5］黄洪钟.模糊设计［M］.北京：机械工业出版社，1999.