物流服务水平影响需求的两个TPL 参与下的供应链博弈分析

王 勇

（上海大学 管理学院，上海 200444）

WANG Yong

(School of Management,Shanghai University,Shanghai 200444,China)

随着信息化技术的发展和市场环境竞争日趋激烈，供应链中企业所需要的物流活动日益庞大和复杂，众多企业纷纷将自己的非核心业务（如物流业务）外包给第三方物流公司，第三方物流（TPL）就是在这样的环境下应运而生的。TPL 高水平、专业化的物流服务，一方面降低了企业的物流成本，另一方面还可以提高企业的客户满意度（如送货速度和送货质量等）。已有研究表明TPL 的物流服务水平满足或超过了顾客的期望时，会促使顾客对产品产生更大的需求，最终使制造商、零售商取得更多的收入和利润。但伴随着越来越多的TPL 的诞生，多个第三方物流企业参与竞争时，多方之间的竞争和合作关系是个亟待解决的问题。

1 文献综述和问题提出

目前，国内外学者们对传统供应链问题的研究已经比较成熟。但斌等针对产品质量影响顾客需求的问题，建立了制造商处于领导地位的二级供应链决策模型，分析了在分散式决策和集中式决策下制造商和零售商关于产品质量的决策。

随着TPL 在供应链的竞争中扮演着越来越重要的角色，让TPL 参与到供应链中来成为供应链中的不可或缺的一员是一种不可阻挡的趋势。公彦德等基于单个制造商、单个TPL 和单个零售商组成的三级供应链系统，将TPL 定量地加入到供应链中来，并在物流服务价格由制造商和零售商共同分担的条件下，应用动态博弈对供应链系统的定价、产量和利润进行了分析。但以上文献仅仅只考虑了供应链结构为1∶1∶1，并没有考虑到有多个第三方物流参与下的供应链结构。

以上的供应链结构过于简单，是因为这种结构研究起来比较顺手，不需考虑多个竞争方之间的竞争。但遗憾的是，这种结构缺少现实普遍性。干华栋研究了以医药流通行业为研究背景，以第三方物流参与下的医药供应链协调与收益分配为研究对象，建立了两个在医药第三方物流参与下的医药供应链博弈模型。

鉴于此，本文把TPL 引入到供应链中来，运用动态博弈对物流服务水平影响产品市场需求的情况下制造商处于主导地位的供应链竞争模型进行了研究。首先，建立一个有两个物流服务商存在情况下进行了独立决策的博弈分析；其次，对集中决策模型进行了研究；最后，通过数据实例的比较得出结论。

2 问题描述和模型假设

考虑两个TPL 企业为一个制造商和一个零售商提供服务，零售商根据产品的市场需求向制造商订货，TPL 从制造商处为零售商送货，顾客对产品的需求除了与产品的价格有关外，还受到TPL 企业的物流服务水平的影响。

假设产品的市场需求函数为Q=a-bp2+θs，式中a,b,θ＞0，都是常数，其中a 表示市场的基础需求量，b 表示价格弹性系数，θ 表示服务弹性系数。

根据相关的文献（刘南，2011），对于第三方物流而言，物流服务水平s 越高，其每单位物流成本h 自然越大，单位物流成本与其自身的服务水平的平方成正比，因此，第三方物流的单位物流成本可以表示为：

式中η＞0，为常数，表示服务成本随服务水平变化而变化的影响系数，此外数字1/2 主要是为了后期求导处理的方便，并无具体意义。

模型的其它符号表示如下：p1：产品的批发价格；p2：产品的零售价格；c1：制造商的单位制造成本；c2：零售商库存、服务等方面的单位成本；s：TPL 提供的物流服务水平，其中TPL1的物流服务水平记为s1，TPL2的物流服务水平记为s2，即s=（s1,s2）；b1：TPL1提供单位产品的物流服务价格；b2：TPL2提供单位产品的物流服务价格；h1：TPL1提供单位物流服务的成本；h2：TPL2提供单位物流服务的成本；Q：零售商的订购量；Q1：经过TPL1产生的订货量；Q2：经过TPL2产生的订货量；η1：TPL1的物流服务水平对其成本的影响系数；η2：TPL2的物流服务水平对其成本的影响系数；πM：制造商的利润；πR：零售商的利润；πTPL1：TPL1的利润；πTPL2：TPL2的利润；πT：供应链整体的利润。

此处，由于存在两个相互竞争的第三方物流，因此对订货量做了如下定义：

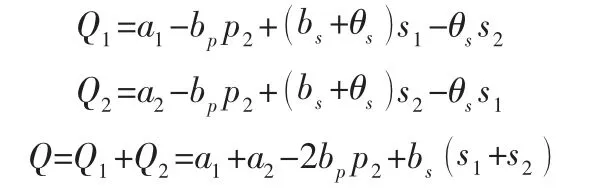
上式中a1,a2,bp,bs,θs都是常数，且都大于0，其中a1,a2表示市场的基础需求量，bp表示价格弹性系数，bs和θs表示服务弹性系数。

同样做了相应的假设:（1）假设只针对单一的制造企业，两家第三方物流之间的信息是公开的，即相互之间知道对方的成本水平；（2）供应链由一个制造商、两个TPL 和一个零售商组成，制造商占主导地位，三者都是追求利润最大化的理性个体，且风险偏好都是中性；（3）假设零售商的订购量就等于产品的市场需求，不考虑存在库存或者是缺货的情况。

3 供应链的决策模型

3.1 分散式决策模型。如果制造商、零售商和TPL 是独立的，三者都本着利润最大化的原则来决策，根据斯坦伯格博弈思想，制造商首先确定批发价后，TPL 根据批发价来决定物流服务水平和单位产品的物流服务价格，然后零售商根据批发价、物流服务水平和价格决定零售价。三者的收益函数分别为：

制造商的利润为：πM=（p1-c1）Q

零售商的利润为：πR=（p2-p1-c2-b1）Q2

TPL1的利润为：πTPL1=（b1-h1）Q1+（p2-p1-c2-b2）Q1

TPL2的利润为：πTPL2=（b2-h2）Q2

由以上参数求得分散式决策下制造商、零售商和TPL 的收益分别为：

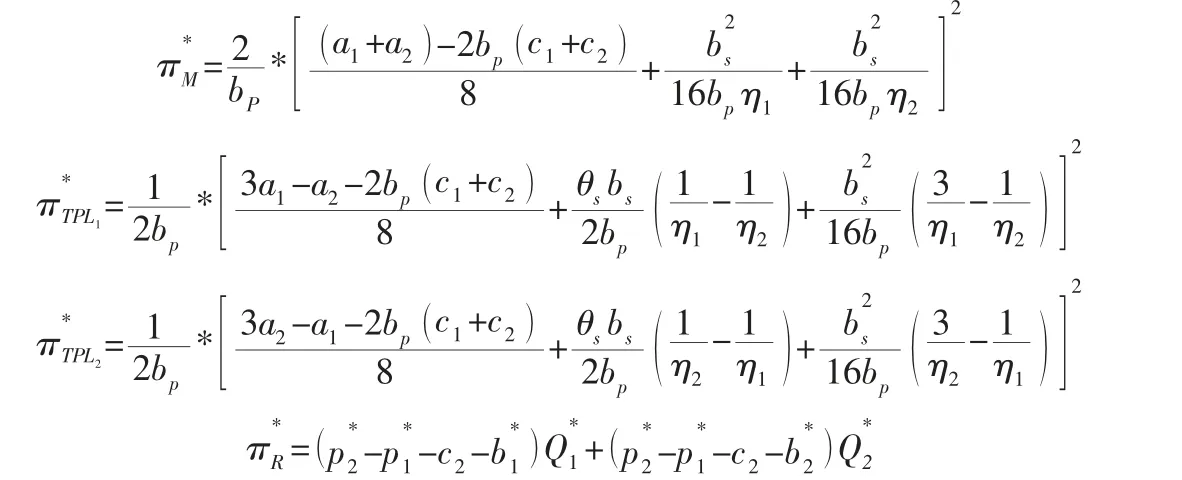
3.2 集中式决策模型。在集中式决策下，制造商、TPL 和零售商组成一个利益整体，集中决策产品的零售价格和物流服务水平。其整体的利润函数如：πT=πM+πR+πTPL1+πTPL2。

为了使整体利润最大，分别求偏导并令导数等于零，解得：

4 算例分析

为了直观的展现独立决策与合作决策的不同结果，将通过数值模拟来对不同决策下的订货量、服务水平、定价、利润等指标进行分析。假设市场的基础需求量a1=50、a2=50；价格弹性系数bp=2；物流成本弹性系数η1=2.5、η2=1.25；服务弹性系数bs=5、θs=1；制造商的单位制造成本c1=5；零售商库存、服务等方面的单位成本c2=1。通过计算，可以得到独立决策和合作决策下，各参数的最优值情况，如表1 所示。

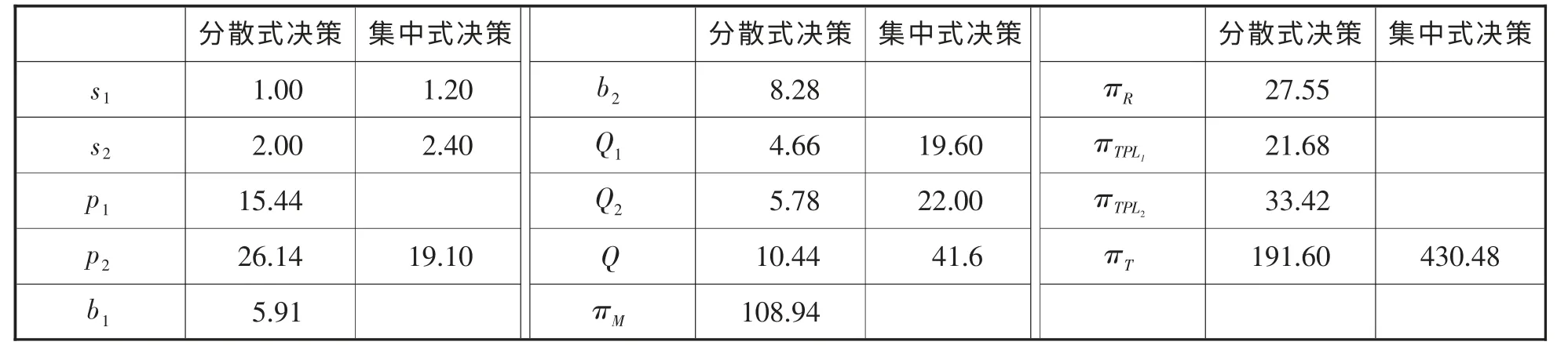
表1 数值模拟计算结果

从表1 可以得出以下结论：（1）集中式决策下，两家第三方物流的物流服务水平都有提升；（2）集中式决策下，零售商的销售价格与分散式决策情况相比，明显下降；（3）集中式决策下，供应链整体的销售量和利润较分散式决策时，有了大幅度的上升。

5 结束语

在前人模型基础上，增加了一个第三方物流，从而引入内部竞争。首先，建立供应链博弈模型，并分别对独立决策过程和合作决策过程两种决策过程进行模型求解。由于模型结果较为复杂，本文直接采用数值分析的方法来直观的分析不同决策下的结果。

本文的模型中只考虑增加一个第三方物流的竞争模型，若多个供应商或多个零售商或多个TPL 服务商之间存在相互竞争，供应链协调策略会发生什么变化需要进一步探讨。

[1]但斌，任连春，张旭梅.质量影响需求下的二级供应链协调模型研究[J].工业工程与管理，2010,15(4):1-4.

[2]公彦德，李帮义，刘涛.3PL 服务提供商参与下的供应链定价及协调策略[J].商业研究，2008(11):162-165.

[3]干华栋.第三方物流参与下的医药供应链协调与收益分配研究[D].杭州：浙江大学（硕士学位论文），2012.

[4]刘南，吴桥，鲁齐辉,等.物流服务商参与时两级供应链的协调策略研究[J].软科学，2011,25(10):125-129.