北斗接收机定位误差分析

张 明，顾晓雪

（中国电子科技集团公司第58研究所，江苏 无锡 214035）

1 引言

目前世界上存在的导航系统有美国的GPS、俄罗斯的GLONASS、欧洲的Galileo以及中国的北斗导航系统。导航系统由空间部分、地面控制中心和用户终端3部分组成，是通过地面接收设备接收卫星传送来的信息，计算同一时刻设备到多颗卫星之间的伪距离，定位被测设备的三维坐标，来实现导航定位。目前北斗导航系统定位精度可达数10 ns的同步精度，其精度与GPS相当。

2 北斗定位原理及误差来源

北斗定位的基本原理是测量出已知位置卫星到用户接收机之间的距离，然后综合多颗卫星的数据就可确定接收机的具体位置[1]。为了得到卫星与接收机之间的距离，需要知道卫星信号到接收机的传播时间，然后乘以光速得到距离。但是由于对流层、电离层干扰存在，这一距离并不是接收机与卫星之间的真实距离，而是伪距（PR）。北斗二代定位系统采用无源定位，卫星系统会不断地发射导航电文。当用户接收导航电文时，提取出卫星时间并将其与自己的时钟进行对比便得到卫星与用户的距离，再利用导航电文中的电离层时延修正、大气折射修正等信息，对距离进行修正。从北斗定位的过程来看，因测量带来的误差，可以全部等效为伪距测量时带来的距离误差，称为用户等效测距误差[2]。

可见北斗卫星定位系统卫星部分的作用就是不断地发射导航电文。由于用户接收机使用的时钟与卫星星载时钟不可能总是同步，所以除了用户的三维坐标x、y、z外，还要引进以Δt即卫星与接收机之间的时间差作为未知数，然后用4个方程将这4个未知数解出来。所以如果想知道接收机所处的位置，至少要能接收到4个卫星的信号[1]。

3 北斗定位误差分类

北斗卫星导航系统主要由空间部分、地面控制管理部分与用户终端组成[3]，对于接收机来说引起北斗定位误差的来源主要有共有误差、传播延迟、接收机固有误差。具体分类如下：

（1）共有误差，包括卫星星历误差、卫星钟差、电离层误差、对流层误差等；

（2）信号传播有关误差，包括信号传播延迟、载波相位周跳和多径误差等；

（3）接收机固有误差，包括观测值噪声、接收机钟差及设备延迟误差等。

表1中显示了不同误差对测距误差的影响估计。

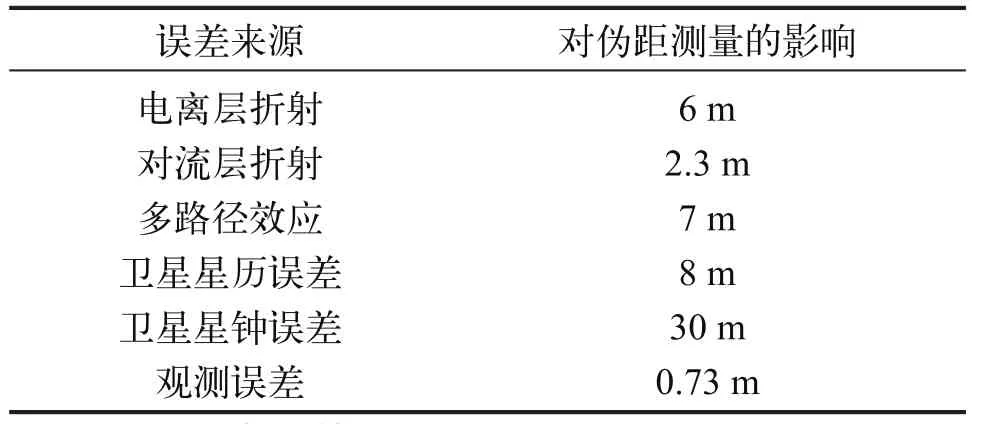
表 1 误差对伪距测量的影响

3.1 同卫星有关的误差

3.1.1 星历误差[4]

卫星星历又称为两行轨道数据（TLE，Two-Line Orbital Element），卫星星历是用于描述卫星位置和飞行速度的表达式——两行式轨道数据系统。卫星星历以开普勒定律的6个轨道参数之间的数学关系确定卫星的时间、坐标、方位、速度等各项参数，具有很高的精度[5]。卫星星历是由地面监控站跟踪监测卫星求定的。由于卫星在运行过程中要受到多种摄动力的复杂影响，而通过地面监控站又难以充分可靠地测定这些作用力或掌握其作用规律，因此在星历预报时会产生较大误差。由星历所计算得到的卫星的空间位置与实际位置之差称为卫星星历误差。

3.1.2 星钟误差[6]

在北斗定位系统中北斗测量均以北斗时间为统一标准，北斗时间由地面控制站确定和保持。在各个北斗卫星中均装置高精度的原子钟，但卫星上虽然装置了高精度的原子钟（铯钟和铷钟），但由于这些钟与北斗标准时之间会有频偏、频漂，并且随着时间的推移，这些频偏和频漂还会发生变化。因此，会导致星钟与北斗时间之间的不同步偏差，这种偏差称为星钟钟差。由于卫星的位置是时间的函数，所以北斗的观测量，均以精密测时为依据，星钟误差会对伪码测距和载波相位测量产生误差，这种偏差的总量可达l ms，乘以光速，可以产生的等效距离误差可达30 km。

3.2 信号传播误差

3.2.1 电离层延迟误差

地球上空60 km以上的大气层基本上都处于部分电离或完全电离状态，其中存在大量的自由电子和正离子，能使无线电波改变传播速度，发生折射、反射和散射。当北斗信号通过电离层时，信号路径会发生弯曲，传播速度也会发生改变。所以信号传播时间与真空中的光速相乘得到的距离就不等于卫星至接收机间的几何距离，这种偏差叫电离层折射误差。

3.2.2 对流层延迟误差

从地面向上约40 km以下范围内的大气层被称为对流层，占整个大气质量的99%。对流层密度很大，对信号传播影响也很复杂，一般对流层对信号的影响有两部分，一是降低传播速度，二是使信号传播路径发生弯曲。另外，对流层的折射率与大气压力、温度和湿度关系密切。

3.3 与接收机有关的误差

3.3.1 接收机钟差

为了测量接收机与卫星的距离，需要在接收机中存在时钟设备，称接收机时钟与卫星系统时钟之间的误差为接收机钟差，其大小取决于所采用的钟的质量。由于信号以光速传播，1 μs的钟差就可以引起300 m的伪距误差。所以在实际测量时要考虑钟差引起的误差。

3.3.2 天线安置误差

接收机天线相对测站点的安置误差，一般认为观测的分辨率误差约为信号波长的1%[2]。由于北斗波长是73 m，所以对定位精度的影响为0.73 m左右。因此，在安装天线时要考虑天线的安装位置、良好避雷等因素，以尽量减小这种误差的影响。

4 解决误差常用方法、模型

针对北斗导航系统3类误差，我们可以采用差分定位方法来消除卫星引起的误差，采用校正模型来消除信号传播的误差，对于接收机引起的误差我们可以改善接收机的性能来予以消除。

4.1 差分定位

采用差分定位可以很好地改善由卫星星历、卫星星钟、电离层、对流层引起的误差。差分定位的原理是，利用一个观测站对两个目标观测值，或者利用两个观测站对一个目标进行观测，或者是一个观测站对一个目标进行两次观测求两次数据差值，目的是消除公共误差项[7]，图1显示的是采用定位校准站对接收设备进行误差校准。

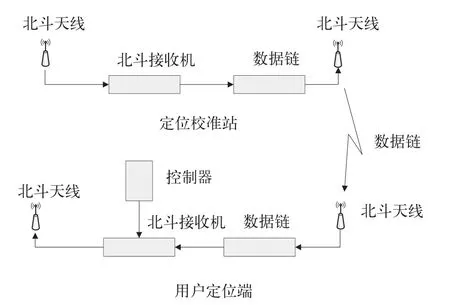
图1 差分定位示意图

通过定位校准站接收机对北斗卫星信号的测量计算出差分校正量，然后将差分校正量播发给被测北斗接收机，以提高用户接收机的定位精度。

4.2 电离层改进模型

电离层改进模型常采用的有广播星历参数改正、单层模型、Klobuchar模型改正以及双频改正等。其中Klobuchar模型能够很好地改善电离层引起的定位误差。下面主要介绍一下Klobuchar模型[8]。

该模型根据电离层延迟随地方时变化的规律，将夜晚电离层延迟看作一个常数，而将白天看作余弦函数的正中部分，利用北斗导航系统在其导航电文中提供的αn、βn（n=0, 1, 2, 3）共8个电离层延迟参数进行电离修正。

其模型改正公式为：

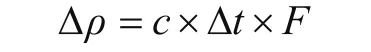
式中Δρ为电离层延迟的伪距修正量；c为光速；Δt为信号L1频率的电离层天顶延迟；F为倾斜因子。Δt和F的表达式分别为：

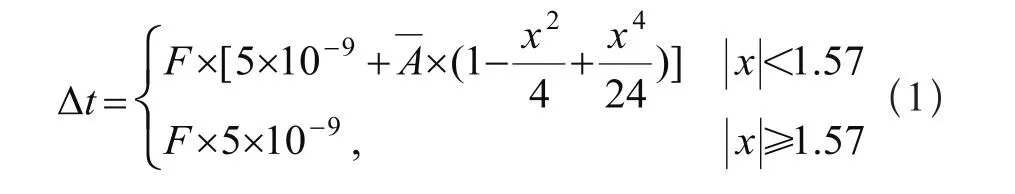
其中：

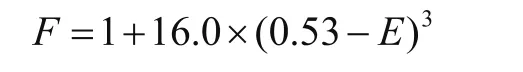
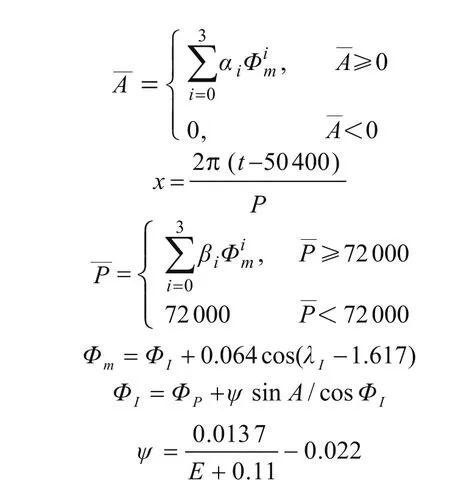
ψ为用户点P与电离层特征点之间的夹角。由于电离层还会受到太阳黑子周期活动的影响，难以只用一种模型来消除电离层误差影响，我们还需要结合多种模型来消除误差影响。

4.3 对流层改进模型

由于对流层占整个大气层的99%以上，对流作用很强，状况变化复杂，对信号的影响主要反映在降低信号传播速度，使信号传播路径发生弯曲。目前常采用霍普菲尔德（Hop field）误差模型进行分析，霍普菲尔德模型经验系数使用18个站的平均资料获得[8]。

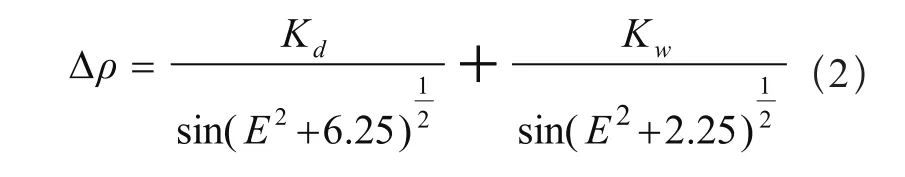
其中Kd为对流层延迟干分量；Kw为对流层延迟湿分量；E为北斗卫星相对于接收机天线的仰角（°）。

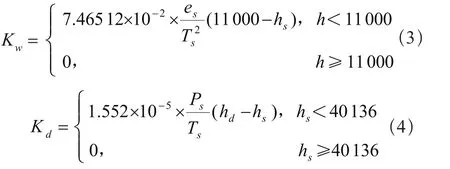
式中Ts为观测站上的绝对温度（K）；Ps为观测站上气压（mbar）；hs为测量站用户的大地高度（m）；es为观测站上的水汽压：

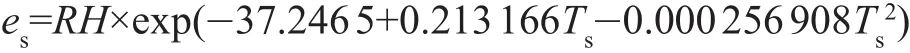
4.4 其他方法

为了解决双星定位精度不高、用户数量不能任意增加、隐蔽性差等问题，还可以采用两星三参数、三星三参数以及三星四参数法等[9]。这些方法都能很好地改善卫星的定位精度，减少测距误差的影响。

5 结束语

在北斗定位系统中，分别从系统的空间部分、地面控制管理部分与用户终端部分，针对引起误差的原因，分别采用差分定位、电离层改进模型、对流层改进模型等方法，能够很好地改善北斗系统的定位精度。这些方法运用一些误差数学模型，进行误差改进，对于定位精度的改善具有实用性和可操作性。

[1] 皮亦鸣，曹宗杰，闵锐. 卫星导航原理与系统[M]. 成都∶电子科技大学出版社，2011.

[2] 郑伟平. 北斗接收机的部分算法与定位误差研究[D]. 哈尔滨工程大学，2006.

[3] 马茹，胡建伟，杨立成. GPS信号和其干扰的Matlab仿真[J]. 电子科技，2011, 24（5）∶ 17-22.

[4] 张清志，唐文清，李军. GPS卫星星历对监测站及基线精度的影响[J]. 沉积与特提斯地质，2012, 3（32）∶106-112.

[5] 周海莺，祝春萌，黄锦渊. 卫星星历及广州气象卫星地面站相关数据分析[J]. 气象水文海洋仪器，2010, 3∶61-63.

[6] 祝彬，郑娟. GPS卫星星钟的发展[J]. 中国航天，2008,3∶ 28-31.

[7] Keith W Alter. Using Wide Area Differential GPS To Improve Total System Error For Precision Flight Operations [D]. USA∶ Stanford University.

[8] 袁建平，罗建军，岳晓奎，等. 卫星导航原理与应用[M]. 北京：中国宇航出版社，2004.

[9] 杨龙，徐冬梅，张守信，董绪荣. 关于北斗卫星导航系统的被动式定位算法比较[D]. 研究空间学报，2006,26（3）∶ 203-208.