数学高考选择题解答应“通”“巧”并举

●李美君(宁海中学浙江宁海315600)

数学高考选择题解答应“通”“巧”并举

●李美君(宁海中学浙江宁海315600)

在数学高考中，选择题是考生必须逾越的第一道屏障.能否迅速、准确、简捷地解好选择题，成为考试成功的关键之一.如果选择题解答不顺，不但意味着失分，而且会给下面的解题带来巨大的心理压力;如果一个选择题是“超时”答对的，那么就意味着已经隐性丢分了.因此在平时教学中，要重视选择题解法的研究与教学，要有意识地渗透选择题的求解策略，以此提高解题的准确性和速度，确保在选择题上得高分的同时，为后续解答赢得时间.那么数学高考选择题的解题技巧是什么呢?

自从《数学通报》1992年第8期发表了曾家鹏先生的文章“提倡运用通法，建议淡化特技”［1］之后，中学数学的舆论出现了“一边倒”现象，对通法推崇有之，对巧法敬而远之，有的甚至谈“巧”色变.然而甘大旺先生在“通法与特技的相对性及启示”一文中强调指出“通法与特技总是相对的，教师对于通法与特技的探索都应该持积极态度而不必顾虑重重”［2］.

基于这样的背景，纵观近几年数学高考选择题，绝大多数题目都可以用通性通法直接求解，但也有许多题目可通过激活思维、创新思考、挖掘其特殊内涵、“巧思妙解”得到答案，因此对数学高考选择题的解答应“通”“巧”并举.所谓通法通常是指解决某一类问题时常用的方法，而巧法就是抓住题目的本质特征，用发散思维和创造性思维来解决问题的方法.本文以2014年浙江省数学高考试卷中比较典型的选择题为例，谈谈“通”“巧”并举在选择题解答中的作用，和大家共享.

1 “通”“巧”并举示例

1.1 通法是“坦途”

例1如图1，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB，某目标点P沿墙面上的射线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小(仰角θ为直线AP与平面ABC所成的角).若AB=15 m，AC=25 m，∠BCM=30°，则tanθ的最大值是()

(2014年浙江省数学高考文科试题第10题)

沉寂了多年的数学应用题，2014年以崭新的面貌再次出现，其实剥去“包装”，这是在三角函数与立体几何交汇处命题的函数最值问题.建立目标函数的方法是解决最值问题的通法，一般步骤是先选择适当的量为变量，再把所需求最值的量用上述变量表示，最后求出上述目标函数的最值即得结论.由于此题有三角函数与立体几何背景，因此用三角公式和建立空间直角坐标系也是通性通法.

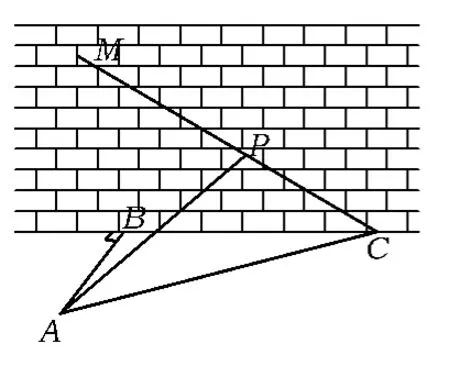
图1

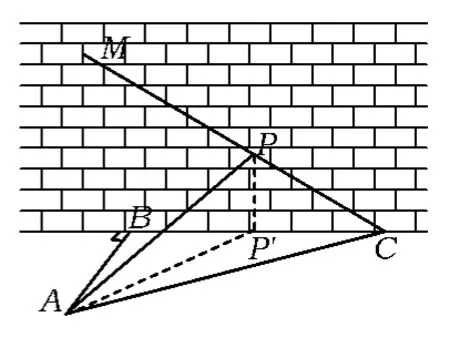
图2

通法1以某一线段长作为目标函数的变量的设法不少，现以设PP'=x为例.

如图2，过点P作PP'⊥BC，交BC于点P'，联结AP'，则∠PAP'即为直线AP和平面ABC所成的角θ，则

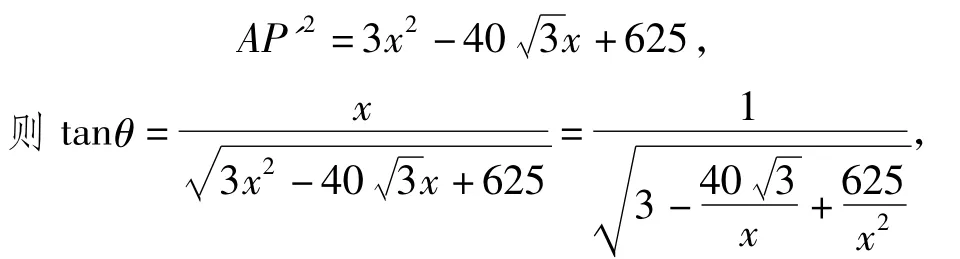
通法2如图2，过点P作PP'⊥BC，交BC于点P'，联结AP'，则∠PAP'即为直线AP和平面ABC所成的角θ，从而易得BC=20，于是

令∠P'AC=φ，在△AP'C中由正弦定理可知

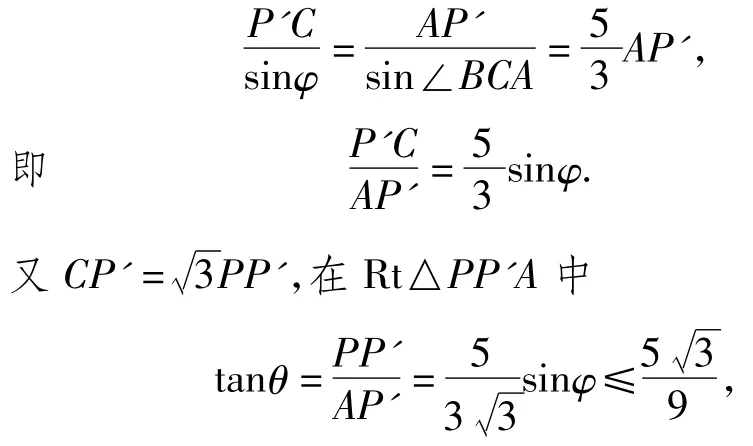
通法3如图3，以B为原点，分别以射线BA，BC为x，y轴的正半轴，建立空间直角坐标系B-xyz.

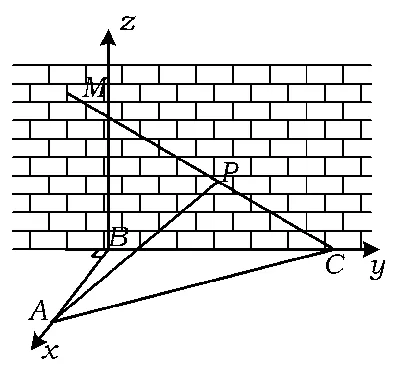
图3

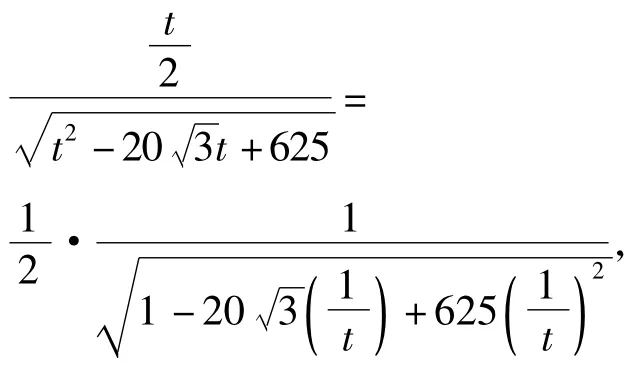
评析通法常以主要的基础知识为依据，以基本方法为技能，它的解法思想顺乎一般的思维规律，其具体的操作过程容易被绝大多数学生所掌握.学生之所以喜欢通法，是因为通法自然、流畅，易于理解，易于掌握和运用.

1.2 巧法是“捷径”

通法是“通途”，而巧法是“捷径”.如2014年浙江省数学高考理科第9题，考生可运用古典概率公式，通过运算硬做，但是运算量较大.若注意到此题是选择题，不需小题大做，则可用特殊值法巧解之.用特殊值法得到答案，有点小“巧”，若抓住概率统计的数学本质:pi(i=1，2)的大小就是取到红球可能性的大小，E(ξ)就是取到红球的平均数，采用稀释思想:若一个球也不放，则从甲盒中取到红球的概率为1，放入i(i=1，2)个球后红球被稀释了，故p1＞p2.而E(ξ2)=E(ξ1+η)=E(ξ1)+ E(η)，由E(η)＞0，知E(ξ2)＞E(ξ1)，这样就“秒杀”答案了.再看下例.

例2设函数f1(x)=x2，f2(x)=2(x－x2)，，i=0，1，2，…，99.记Ik=|fk(a1)－fk(a0)|+|fk(a2)－fk(a1)|+…+ |fk(a99)－fk(a98)|，k=1，2，3，则()

A.I1＜I2＜I3B.I2＜I1＜I3

C.I1＜I3＜I2D.I3＜I2＜I1

(2014年浙江省数学高考理科试题第10题)

此题主要考查了二次函数、三角函数、绝对值、比较大小等知识和技能，通法就是去掉绝对值，结合函数知识进行大小比较.但对I3的计算过程中，牵涉到带绝对值的三角函数的单调性，图像翻折后对2个数的大小进行比较，稍不留神就会出错，且得到后，想到

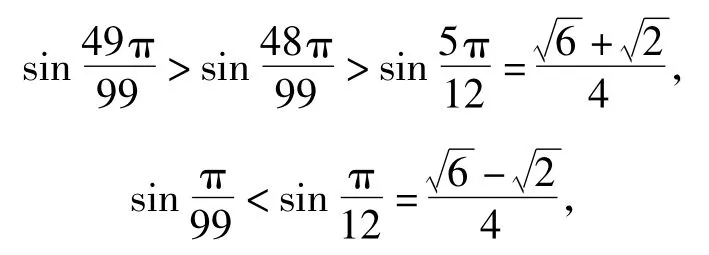
得到I3＞1也不容易.考生若能够抓住问题的本质特征，结合函数图像先分析后估算，就能使问题的解决既直观又“入微”.

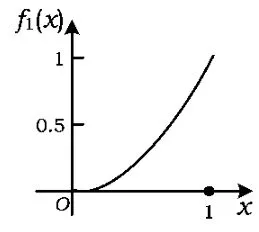
图4

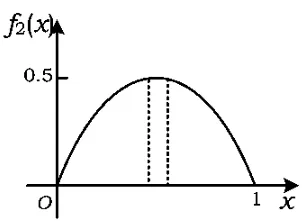
图5

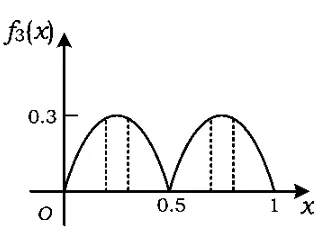
图6

巧法由图4可知，因为f1(x)在［0，1］上单调递增，所以

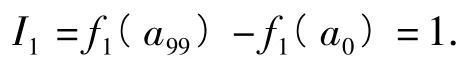
由图5可知，f2(x)在上单调递增，在上单调递减.因此从f2(a1)到f2(a49)是单调递增的，从f2(a50)到f2(a98)是单调递减的，这样把I2分成2段之和，可得

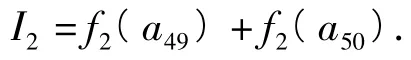
由图像可知，f2(a49)，f2(a50)均比小，故I2＜1.

由图6可知，f3(x)在上单调递增，在上单调递减.因此从f3(a1)到f3(a24)是单调递增的，从f3(a25)到f3(a49)是单调递减的，从f3(a50)到f3(a74)是单调递增的，从f3(a75)到f3(a99)是单调递减的，这样把I3分成4段之和，从图中可以看出每一段的值均接近.因此I3接近，故I2＜I1＜I3.

评析让I1，I2，I3与1，比较大小后得出结论，不能不说是“巧”，但“巧”得恰当，“巧”得合理，“巧”得科学，“巧”得精彩.巧法的特点是对题目“个性”把握得准确而深刻，是抽象、概括、发散、合情推理的产物，是思维活跃、浓缩的结果.

1.3 “通”“巧”并举效果好

通法在一定范围内具有普适性，是解决问题最常用的方法，而巧法往往在解答选择题的速度上、简化解题过程上有着特殊的效果，因此“通”“巧”并举效果好.

例1的巧法设点P固定，那么点P到平面ABC的距离确定，让点A在射线CA上运动，要使仰角最大，只要点P到直线AC的距离最短(如图7).因此，当AP⊥AC时，仰角最大.

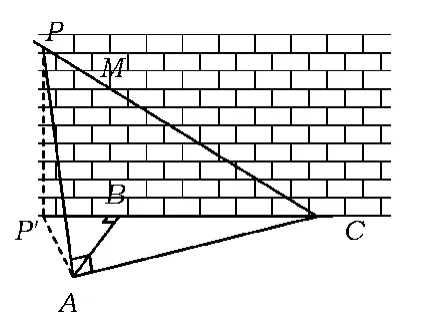
图7

过点P作PP'⊥BC，交BC于点P'，联结AP'，则

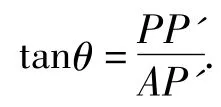
设CP=t，在Rt△PP'C中，

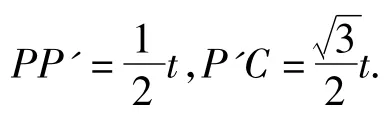
在Rt△P'AC中，

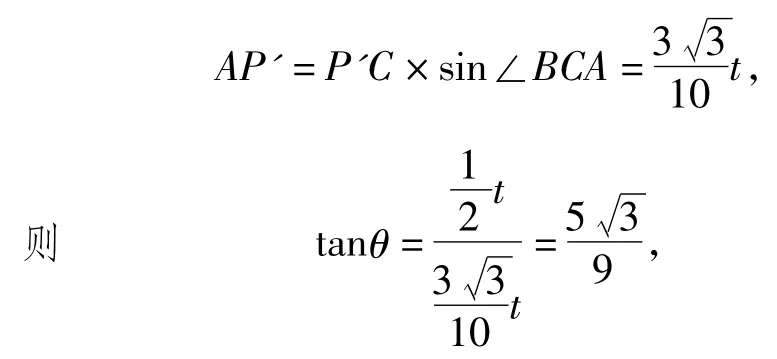
评析这是令人拍案叫绝的解法，但其不足之处也很明显，就是不容易想到，必须要看清此题是给静态的函数图像问题加入了“动态”的元素，而动静是相对而言的，才能想到“动静互转”这类巧法.而上述3种通法，无疑是绝大多数考生的选择，无需太多的思维能力，只需“手工劳作，一算到底”，但是运算过程比较繁难，且费时费力.因此“通”“巧”并举可使不同层次的学生从自身的实际出发选用不同层次的方法，都能保证解题的准确性.

2 “通”“巧”并举的优势

通法解题思路的定势作用有积极的一面，即对于同一类型的题目，能使学生按照定型化的思路，驾轻就熟地解决问题，但有时方法繁琐，运算量大，容易出错，对培养学生思维的敏捷性和创造性有消极的作用，阻碍了学生思维的发展.“巧法”思维航程短，巧妙地利用题中的隐蔽条件，在开拓学生思路、锻炼学生能力上有着独特的功能，它往往还能给人以某种形式美的享受，但思维层次高，运用面相对较窄，没有扎实的基础，在短时间内是不易想到的.过分强调通法会影响发散思维和创造性思维的培养，而过于注重巧法也会导致缺乏对基本思想、方法的挖掘和相应的训练，从而冲淡和掩盖了对基本思想方法的渗透，因此两者各有利弊.

立足于基础的通法应是选择题解答的主力军，而注重能力的巧法必须作为一种重要方法经常使用，通法与巧法相辅相成，则是一种更高的思维层次.在学习中要弄清通法和巧法的适用范围，充分发挥通法和巧法各自的教学功能，应用中宜“通”“巧”并举，选择最适合自身思维能力的解法.“通”“巧”并举不仅能让学生有“什么类型的题目用什么方法”的意识，还能从通性通法中跳出来，积极地开展创造性思维活动，进一步优化学生的思维品质，提高分析问题和解决问题的能力.

3 如何做到“通”“巧”并举

著名数学教育家波利亚说:“中学数学的主要任务就是解题训练”，而解题教学的关键之一是帮助学生制定最佳的解题方案.既然在数学选择题解答中“通”“巧”并举有诸多优势，那么如何才能实现呢?笔者认为至少要做到以下2点:

1)树立务实的解题理念.当下，高中数学教学对选择题的解答往往运用通性通法，认为只有通过正确的推理演算得出的结果才放心，扼杀学生“不常规”的思维亮点，要求学生“做出答案，不准猜答案”.长久以往，学生不敢“瞎想乱猜”，只能一味地埋头死算(推)，小题大做，既费时又易出错，无法实现高考选择题的速解.当然在平时教学中，采用大量巧法，必定会使部分学生对数学产生恐惧心理，认为数学“高不可攀”，从而丧失学好数学的信心.因此在平时的选择题教学中，既要注重通性通法的掌握与数学思想方法的揭示，又要充分利用选择题“不需要写出推理过程，四选一”的特点，运用“特例法”、“数形结合法”、“估算法”等选择题解答的独特技巧，达到巧解、快解与通法兼容并包的效果.只有在平时学习中树立起“既要重视通法，又要追求巧法”、“小题小做、小题巧做”等务实的选择题解题理念，才能在高考中实现解题角度的灵活变通与解题方法的灵活选择.

2)养成解题反思的习惯.当前选择题教学还存在一些误区，主要是“重结果，轻过程”，较少暴露“怎样解题”的思维过程，更不去思考“为什么这样解”，缺少对解题过程和思想方法的反思和理解.解题反思是训练和提高学生思维能力的重要途径，是提高解题能力的重要环节，是对思维过程、思维结果进行再认识的检验过程.因此在教学中一定要舍得花时间引导学生反思，给学生充分“悟”的时间，没有“悟”性的学生，就很难有思维的灵活性.让学生学会做完一道选择题时，反思为什么要用这种方法，是否还有更好的方法，哪一种方法最优，等等.如例1，反思解题方法，抓住“动静相对而言”的特点，采用“动静互换”的解题方法，就使学生的思维更具灵活性;又如例2，在运用通性通法顺利解出答案后，反思题目的本质特征是什么，运用数形结合和估算法，使学生的思维更具广阔性.因此在高考选择题解答中要实现“通”“巧”并举，就要在平时训练中，多引导学生养成解题反思的习惯，日积月累，在潜移默化中提高解题能力，形成技能.只有这样，才能在高考时充分利用题目自身提供的信息，化通法为巧法，避免小题大做，真正做到准确和快速.

解选择题应掌握对应的基本知识，运用常规的解题思想，更应充分挖掘题目的信息，综合运用各种方法，迅速地做到小题巧做，因此“通”“巧”并举是高考数学选择题解答的良策之一.

［1］曾家鹏.提倡运用通法，建议淡化特技［J］.数学通报，1992(8):16-17.

［2］甘大旺.通法特技的相对性及启示［J］.数学通报，1997(2):11-12.