轴承/密封耦合作用下流体激振特性研究

张万福，杨建刚，李 春

（1.上海理工大学 能源与动力工程学院，上海 200093；2.东南大学 火电机组振动国家工程研究中心，南京 210096）

轴承/密封耦合作用下流体激振特性研究

张万福1，杨建刚2，李 春1

（1.上海理工大学 能源与动力工程学院，上海 200093；2.东南大学 火电机组振动国家工程研究中心，南京 210096）

以转子—轴承—密封系统为对象，建立轴承/密封耦合作用对系统动力特性影响的有限元模型。分别应用有限差分和CFD方法对轴承、密封动力特性系数进行求解。理论研究表明密封对转子不平衡响应的影响主要集中在共振区域。通过在密封入口引入负预旋可以提高系统的稳定性，密封气流力对系统稳定性影响随转速的升高也越来越大。通过选择合适的轴承型式可以补偿密封气流力对系统稳定性带来的不利影响。试验发现随着转速增加，试验转子在5 000 r/min附近时开始出现比较明显的半频分量，而且随着转速继续增加，半频分量的幅值变大。密封流体激振力的存在促进轴承内油膜失稳故障发生，影响系统稳定性。

振动与波；密封；流体激振；轴承；计算流体力学；稳定性

密封是大型旋转机械抑制流体泄漏的关键部件。近年来随着机组向大容量、高参数方向发展，越来越多的不稳定振动故障相继被报导于汽轮机高中压缸中。转子的稳定性往往受轴承和密封共同作用的影响，目前多数研究都是单独地研究轴承、密封对转子系统稳定性的影响[1-7]。2008年，Hirano[8]分析了梳齿密封对某大型汽轮发电机组稳定性的影响，表明该机组运行在稳定的范围内。2009年，Wang[9]研究了转子—轴承—密封系统的非线性动力特性，结果表明交错齿密封不利于系统的稳定。2011年，Li[10]提出了一种新的基于Hamilton原理的转子—轴承—密封系统非线性模型，并进行了数值分析。这些研究侧重于转子—轴承—密封系统的非线性特性[11]，而且多数都是以Jeffcot转子为对象，并作了很多假设条件，忽略了陀螺效应等因素的影响。

本文针对转子—轴承—密封系统，研究了轴承/密封耦合作用下转子（非）同步振动特性。基于CFD方法求解得到密封动力特性系数，建立了转子—轴承—密封系统有限元模型，并通过试验研究了轴承/密封作用下转子不稳定振动特性。

1 转子—轴承—密封系统动力特性数值分析

1.1 转子—轴承—密封试验系统

转子—轴承—密封系统试验台如图1所示。转子总长为1 200 mm。转子中部为试验段，为了与静子配合形成所需要的密封结构，轴上嵌套安装一个直径为180 mm、长度为430 mm的轴套。转子通过两个圆瓦滑动轴承支撑。轴承宽度为44 mm，轴承直径为50 mm，直径间隙为0.05 mm。润滑油采用L-TSA32号透平油。

图1 转子—轴承—密封试验系统

1.2 转子—轴承—密封系统动力特性数值分析

数值计算基于上述转子—轴承—密封系统试验台。为了研究轴承性能对系统稳定性的影响，选取了多组轴承，如表1所示。而试验台中所使用的实际轴承参数为其中的Case 2，轴承动力特性系数通过有限差分方法求解。

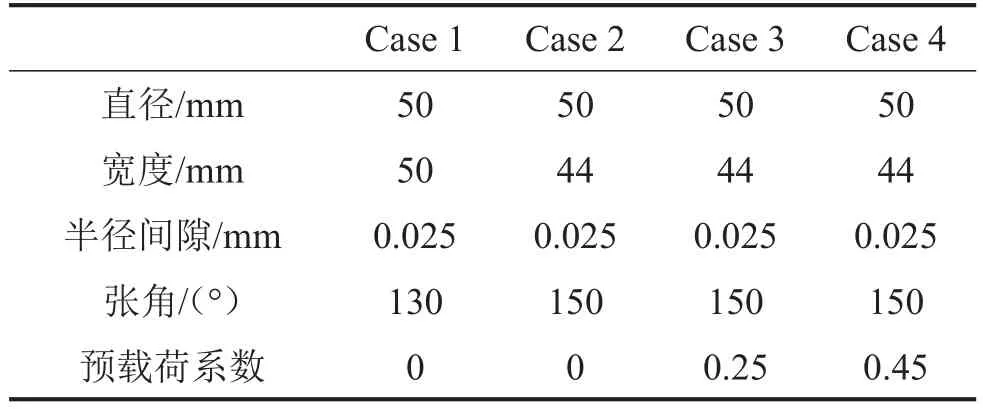
表1 轴承几何参数

密封动力特性系数基于CFD旋转坐标系方法求解，密封三维CFD模型如图2所示。此外，为了研究进口预旋对密封动力特性的影响，分别对零预旋、正预旋（30°）和负预旋（-30°）三种情况进行了计算。

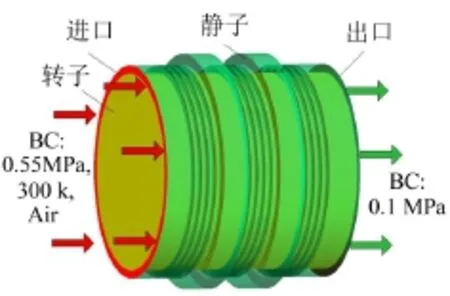
图2 密封计算模型及边界条件

计算结果表明，随转速升高密封交叉刚度系数绝对值与交叉阻尼系数都逐渐增大，而直接刚度系数和直接阻尼系数绝对值略微减小。正预旋会增大交叉项系数，降低直接项系数。负预旋的作用则呈正好相反趋势。可以看出在转子自转转速提高时，不利于系统的稳定，尤其是当入口增加的预旋和转子转速方向一致时，即正预旋时，系统稳定性将越来越差。

应用ANSYS建立转子—轴承—密封系统有限元模型，密封对系统的影响通过密封动力特性系数等效到系统中，如图3所示。

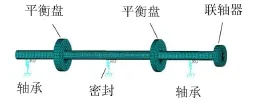
图3 转子—轴承—密封系统有限元模型

图4给出了在没有预旋情况下气流力对转子不平衡响应的影响。转子1阶临界转速大约为2 700 r/ min。可以看出在有密封和没有密封两种情况下，转子不平衡响应有很大差异。密封对转子不平衡响应的影响主要集中在共振区域，而对其他转速影响较小。在气流力的作用下转子在共振区域附近的不平衡响应明显降低，这主要是由于密封流体激振力引起的阻尼作用在这一区域占优，阻尼会消耗转子振动能量，从而使转子的振动幅值减小。

通过计算转子对数衰减率来评价系统稳定性，其值若大于零系统就会失稳。图5给出了转子—轴承—密封系统1阶对数衰减率随转速变化情况。可以看出：

（1）在没有密封气流力作用下，失稳转速约为5 116 r/min；

（2）有密封气流力作用时，与零预旋、正预旋、负预旋三种工况对应的失稳转速分别为5 053 r/min、4 940 r/min、5 200 r/min，说明在气流力的作用下，系统失稳转速可能提前也可能滞后；

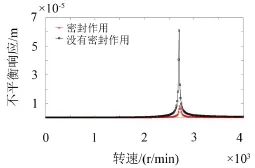
图4 气流力对转子不平衡响应的影响

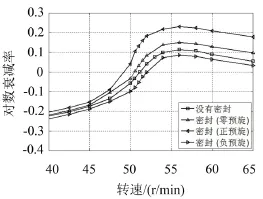
图5 密封对转子1阶对数衰减率的影响

（3）通过在密封入口引入负的预旋可以提高系统的稳定性；

（4）密封气流力对系统稳定性影响随转速的升高也越来越大。

图6给出了这4种不同轴承型式下系统失稳转速的变化，可以看出：

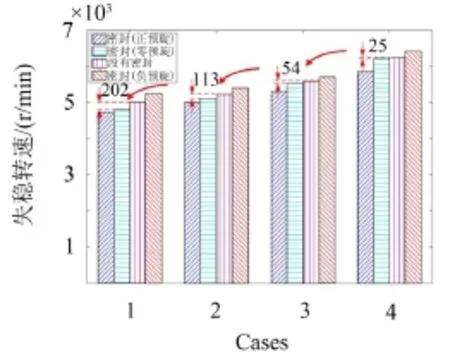
图6 不同轴承型式对系统失稳转速的影响

（1）在没有密封气流力作用下，系统失稳转速从Case 1到Case 4逐渐增大；

（2）对比没有气流力作用和有气流力作用（零预旋）两种情况，两者失稳转速在Case 1下的差别最大，为202 r/min，Case 4下两者相差最小。导致上述结果的主要原因是在这4种轴承型式中，与Case 1对应的轴承具有最差的性能，依次为Case 2、Case 3、Case 4。可见轴承性能的好坏对系统稳定性有着非常关键的影响，通过选择合适的轴承型式可以补偿密封气流力对系统稳定性带来的不利影响。

2 转子—轴承—密封系统动力特性试验研究

为了分析密封流体激振力对转子—轴承系统动力特性的影响，首先试验研究了流体激振力作用下，升速过程中转子绝对振动（轴振）的变化情况。由于转子振动在临界转速附近变化比较明显，因此重点研究了充气前后转子在临界转速附近的振动变化。图7和图8给出了传统梳齿密封下充气和未充气两种状态时转子绝对振动的升速伯德图。

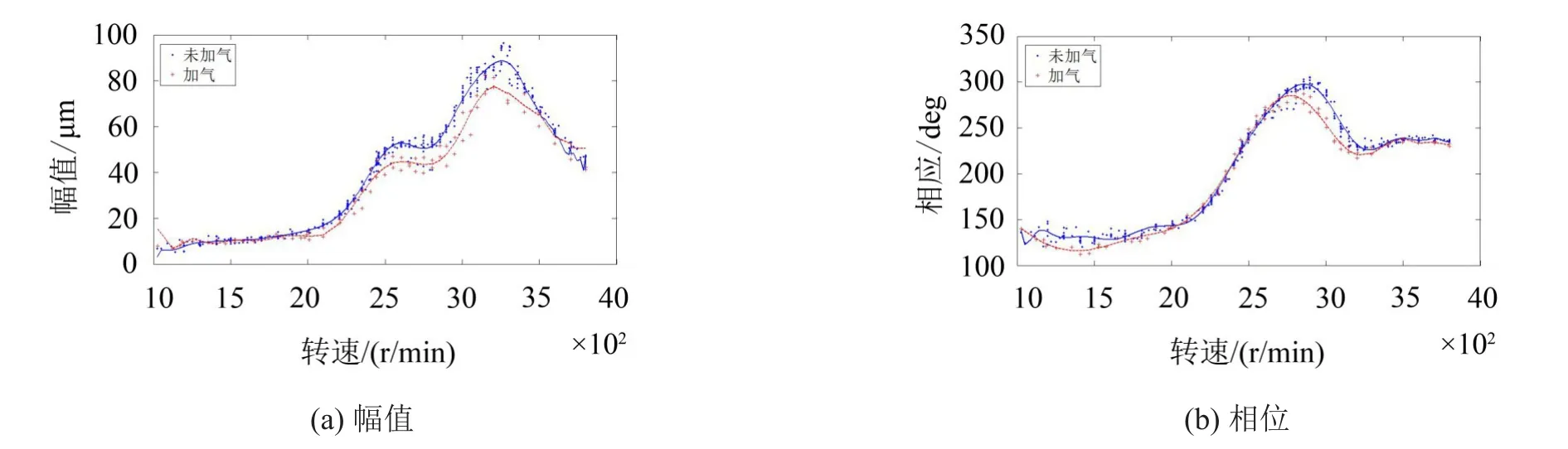
图7 充气和未充气状态下水平轴振升速曲线

可以看出，水平方向转子临界转速在2 400 r/ min左右，垂直方向临界转速在3 200 r/min左右。水平方向升速幅值曲线上除了在水平临界点2 400 r/ min附近有较大峰值外，还有一个3 200 r/min左右的峰值，垂直方向上除了本身临界点3 200 r/min附近有较大峰值外，在2 400 r/min附近存在一个较小的峰值，这是由于转子轴振存在垂直和水平方向的耦合效应所引起。密封流体激振力对轴振的影响主要表现在水平临界转速和垂直临界转速之间的区域。在临界转速附近，加气状态下轴振幅值要小于未加气状态幅值，说明在该点附近密封流体激振力引起的阻尼作用占优，阻尼会消耗转子振动能量，从而使转子的振动幅值减小。从垂直和水平振动相位变化图上看，进气前后相位变化较小。

从转子—轴承—密封系统稳定性的数值研究可以看出，密封内流体激振力会导致转子失稳提前或滞后，在试验台轴承/密封作用下，转子失稳故障会提前发生。试验发现在不进气状态逐渐提高转子转速到转子振动半频分量大量出现，确定出现油膜失稳的转速范围，然后在进气状态下，调节入口压力稳定在0.5 MPa，逐渐提高转速，记录引入密封流体激振力后转子绝对振动各频率分量的变化情况。图9给出了传统梳齿密封进气和未进气两种状态下，轴承#2轴振各频率分量幅值随转速的变化情况。

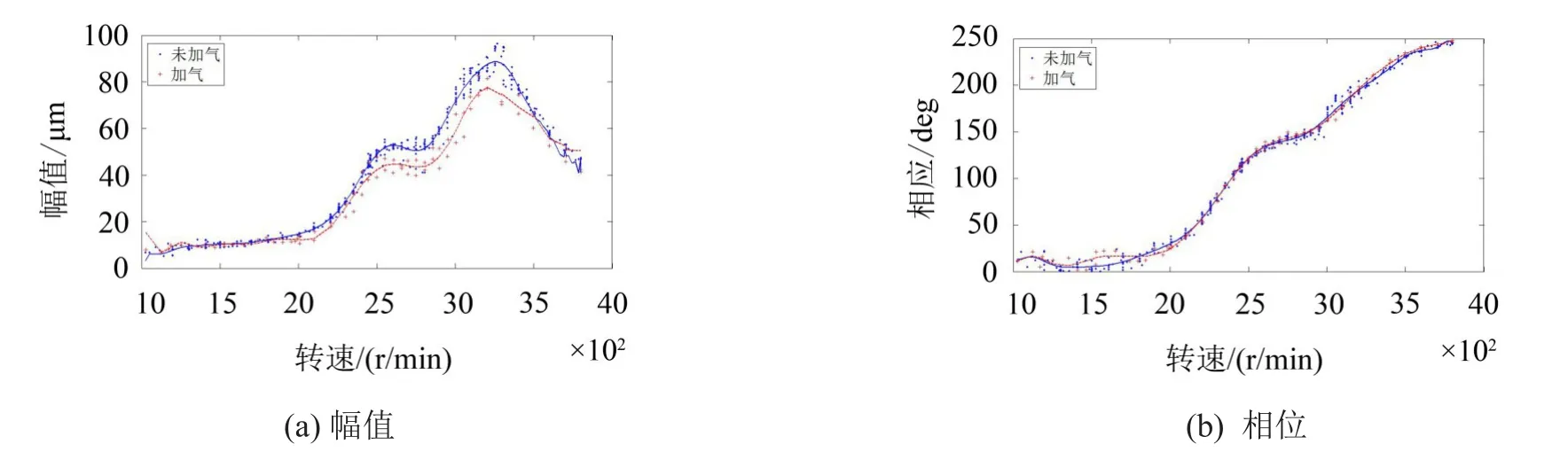
图8 充气和未充气状态下垂直轴振升速曲线

可以看出，转子升速过程中，初始阶段振动幅值以工频分量为主，能明显地看出垂直临界转速在3 200 r/min附近，水平临界转速在2 400 r/min附近。未加气状态时，随着转速增加，在5 000 r/min附近时开始出现比较明显的半频分量，而且随着转速继续往上增加，半频分量的幅值变大，此时试验台转子发生油膜失稳故障。对比加气状态时同一个测点位置的升速瀑布图，可以发现在加气状态下，半频分量出现的转速位置提前。轴振半频分量出现所对应的转速已经由5 000 r/min提前到4 800 r/min附近。随着转速继续往上增大，加气状态下的半频分量幅值随转速增大的趋势比未加气状态更明显。

试验中还发现，1倍频分量在加气前后变化不大，而1/2倍频（半频）分量加气前后变化明显。转速为5 156 r/min时，1#垂直、2#垂直、1#水平、2#水平轴振半频分量幅值加气后与加气前比值分别为2.054、2.383、1.709、2.312。由此可以看出，密封流体激振力的存在，会促进轴承内油膜失稳故障发生，影响转子系统的稳定性。如果进气压力提高，压比增大，这种变化趋势将越明显。实际汽轮发电机组密封进气压力和压比都远大于试验台进气压力，可以推断密封力对转子轴承系统稳定性的影响将更大。

3 结语

针对转子—轴承—密封系统对轴承/密封耦合作用下流体激振特性进行了数值和试验研究，结果表明：

（1）密封对转子不平衡响应的影响主要集中在共振区域，通过在密封入口引入负的预旋可以提高系统的稳定性，密封气流力对系统稳定性影响随转速的升高也越来越大；

（2）轴承性能的好坏对系统稳定性有着非常关键的影响，通过选择合适的轴承型式可以补偿密封气流力对系统稳定性带来的不利影响；

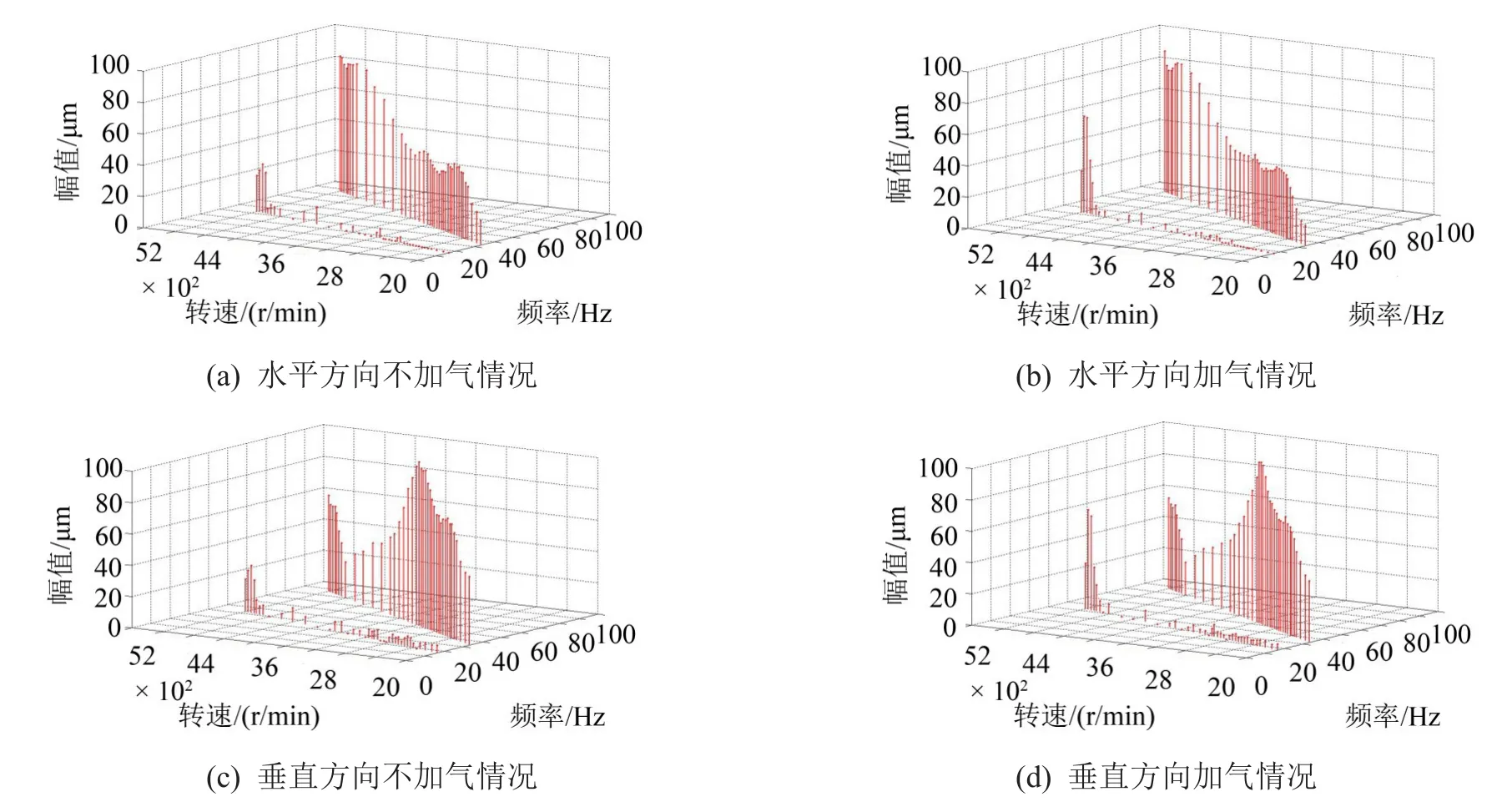
图9 轴承2#轴振加气和不加气状态下瀑布图

（3）在临界转速附近试验密封流体激振力引起的阻尼作用占优，会消耗转子振动能量，从而使转子的振动幅值减小；

（4）随着转速增加，试验转子在5 000 r/min附近时开始出现比较明显的半频分量，而且随着转速继续增加，半频分量的幅值变大，此时试验台转子发生油膜失稳故障；

（5）密封流体激振力的存在，会促进滑动轴承内油膜失稳故障发生，影响系统稳定性。

[1]Rajakumar C,Sisto F.Experimental investigations of rotor whirl excitation forces induced by labyrinth seal flow[J]. Rotating Machinery Dynamics,1987,112(4):263-272.

[2]Muszynska A.Stability of Whirl and Whip in Rotor Bearing Systems[J].Journal of Sound and Vibration, 1988,127(1):49-64.

[3]Yucel U.Effects of labyrinth seals on the stability of rotors [D]:Lehigh University,2000.

[4]Qin P,Shen Y,Zhu J,et al.Dynamic analysis of hydrodynamic bearing-rotor system based on neural network[J].International Journal of Engineering Science,2005,43(5):520-531.

[5]Akmetkhanov R,Banakh L,Nikiforov A.Flow-coupled vibrations of rotor and seal[J].Journal of Vibration and Control,2005,11(7):887-901.

[6]Hua J,Swaddiwudhipong S,Liu Z S,et al.Numerical analysis of nonlinear rotor-seal system[J].Journal of Sound and Vibration,2005,283(3-5):525-542.

[7]孙炳南，谢帆，荆建平.轴承支撑特性对轴系稳定性影响[J].噪声与振动控制，2012，32(6)：137-140.

[8]Hirano T,Sasaki T,Sakakida H,et al.Evaluation of rotordynamic stability of a steam turbine due to labyrinth seal force[J].Journal of Power and Energy Systems, 2008,2(3):945-955.

[9]Wang W Z,Liu Y Z,Meng G,et al.Nonlinear analysis of orbital motion of a rotor subject to leakage air flow through an interlocking seal[J].Journal of Fluids and Structures,2009,25(5):751-765.

[10]Li W,Yang Y,Sheng D,et al.A novel nonlinear model of rotor/bearing/seal system and numerical analysis[J]. Mechanism and Machine Theory,2011,46(5):618-631.

[11]沈小要，赵玫.转子—轴承—密封系统非线性动力学理论和试验研究[J].噪声与振动控制，2009，29(6)：67-71.

Research on Fluid-induced Vibration Characteristics under Coupling Effect of Bearings and Seals

ZHANG Wan-fu1,YANG Jian-gang2,LI Chun1
(1.School of Energy and Power Engineering,University of Shanghai of Science and Technology, Shanghai 200093,China; 2.National Engineering Research Center of Turbo-generator Vibration,Southeast University, Nanjing 210096,China)

Finite element model of a rotor-bearing-seal system was set up to study the influence of the coupling effect of bearings and seals on the system characteristics.Finite difference method and CFD method were employed to obtain the dynamic coefficients of the bearings and seals.Theoretical studies show that the seal has a large influence on the synchronous response of the rotor in the resonant region.Negative preswirl at the inlet of the seal tends to improve the system stability.Influence of the seal force on the system stability becomes more and more serious with the increasing of the rotating speed.Results also show that the detrimental influence of the seal can be compensated by using suitable bearings. Test results show that the subsynchronous vibration appears at about 5 000 r/min,and it becomes larger and larger with the increasing of the rotating speed.The existence of the seal force tends to promote the occurrence of instability faults in bearings and affect the system stability.

vibration and wave;seal;fluid-induced vibration;bearing;computational fluid dynamics(CFD);stability

TK263

A

10.3969/j.issn.1006-1335.2015.03.024

1006-1355(2015)03-0112-05

2014－04－25

国家自然科学基金项目（11402148；51275088；51176129）

张万福，男，河南固始人，博士生，主要研究方向：转子动力学、流体激振研究。E-mail:zwf5202006@163.com

杨建刚，男，江苏如皋人，博士生导师，主要研究方向：转子动力学和旋转机械振动故障监测和诊断研究。E-mail:jgyang@seu.edu.cn

通讯作者：李春，男，北京人，博士生导师，主要研究方向：动力机械特性及现代设计方法、叶轮机械内部流动与性能优化设计。E-mail:lichunusst@163.com