模糊评价法在高职院校学习质量评价中的应用

刘翠梅，顾卫杰

模糊评价法在高职院校学习质量评价中的应用

刘翠梅，顾卫杰

针对高职院校学生学习质量评价过程中标准不统一、受主观因素影响大等问题，从高职院校学生职业能力培养的三个方面(专业能力、社会能力、方法能力)，构建高职院校学生学习质量评价指标体系，并将模糊评价法引入到学习质量的评价中，给出了模糊评价法的基本步骤和结果。

高职;学习质量;评价指标;模糊评价

改革开放在促使经济快速发展的同时，也推进了我国教育事业的发展。高职教育的主要特征就是培养适应地方经济发展所需的技能型人才，在人才培养过程中，教学是主要途径，因此，教学质量直接关乎着人才培养的质量。目前，国内关于教学质量的研究绝大部分集中在“教”的层面，讨论“教什么”、“怎么教”等问题;而从“学”的视角，探寻“为什么学”、“学得怎样”，进而关注大学生的学习状态和内心感受、有效改善学习状况、提高学习成效和质量等实质性问题，则研究的不多，评价方法主要以专家论证定性评价方法为主，标准不统一，受主观因素影响大。［1］同时，学习质量的评价标准带有一定的模糊性，传统的评价方法已无法准确反映实际指标的内涵。

本文试在高职院校学生学习质量评价中引入模糊数学的概念，具体学习质量评价指标的权重由构造模糊一致判断矩阵［2］来确定，将评价主体的个人评判与数学模糊相结合，使定性评价问题转为定量评价问题。从而在很大程度上避免了定性评价不足和主观判断失误所造成的影响，使学习质量评价体系更具有科学性和可操作性。

一、构建学习质量评价指标

(一)选择学习质量评价指标

高职学生的学习质量评价是高职教育中的重要环节，因此，如何真实地反映学生的学习质量应成为高职教育关注的重点。而在建立学习质量评价之前，必须弄清楚学习质量存在哪些主要影响因素与制约因素，这些因素之间有着怎样的关系，它们对实现教学质量的终极目标又有着怎样的影响等问题。

学习活动全过程可分为三个阶段:学习基础、学习过程、学习效果。其影响因素包括学习方法、习惯，知识技能接受程度，团队精神，职业素质等方面。通过对学习质量评价因素的分类，最终选择三个一级指标:专业能力、社会能力、方法能力;再把三个一级指标细分为多个观测点，形成二级指标;同时，给出每个观测点的具体评价要求，从而构成表1所示学习质量评价指标体系(各指标权重确定方法见下文)。

(二)确定指标的评价标准

理论上，随着评价等级数量的增多，评价的精确度会越高，但考虑到一般人的接受与掌握程度，评价标准等级通常选3－5个为宜。本文中评价结果采用五级制:“优”、“良”、“中”、“合格”、“不合格”。

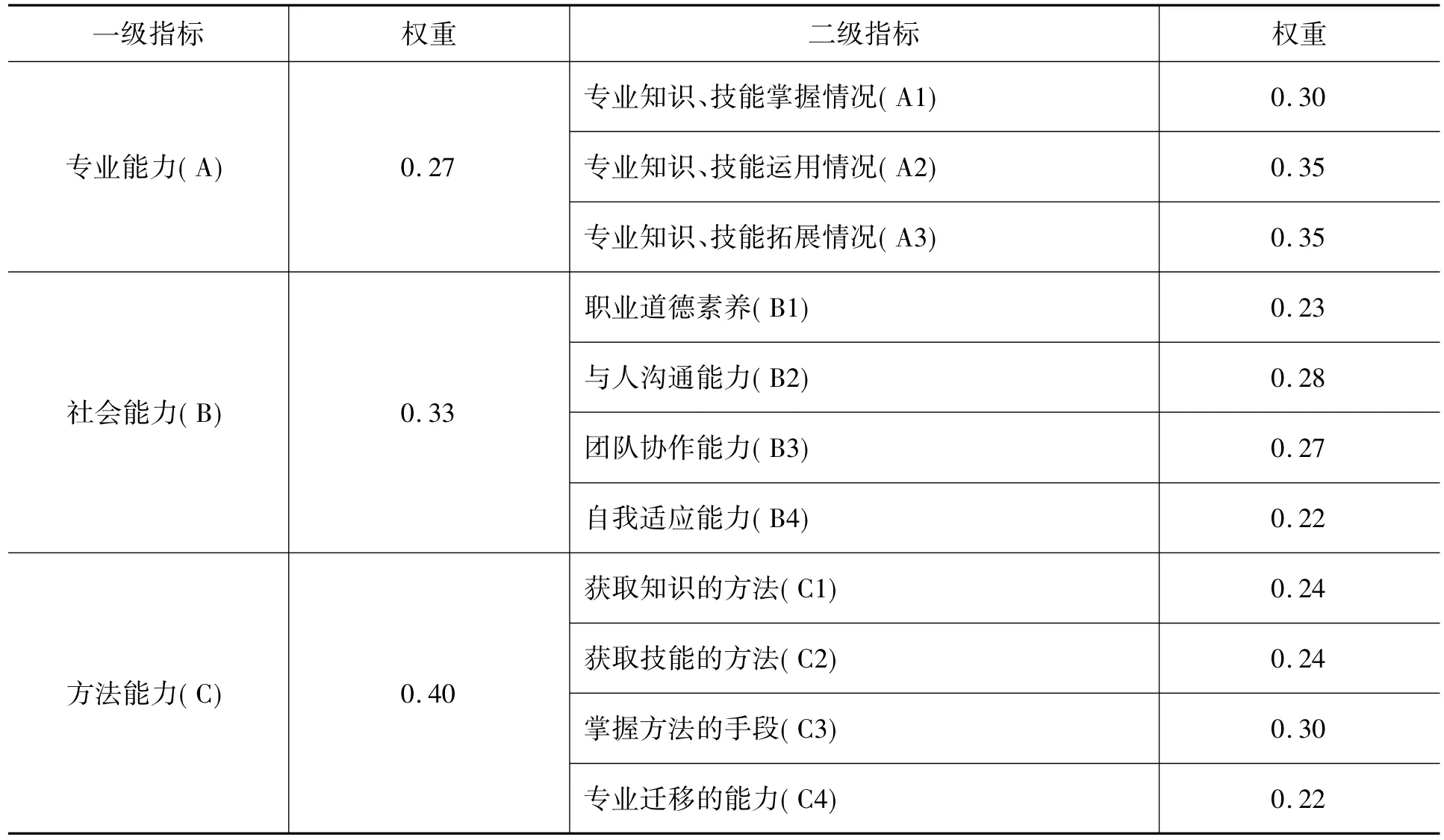
表1 学习质量评价指标体系

在评价过程中，评价者从评价主体的需求出发，基于事物满足需要程度的基本准则，来确定评价内容的具体价值。在学习质量的评价过程中，需从学生自身发展、学校办学目标、培养学生职业能力的完整性以及与社会的吻合度等三个方面，来衡量学习质量所能达到的等级。由于篇幅原因，本文在此不一一列出全部二级指标的评价标准，仅以表2所示二级指标A1的评价标准为例，其余的评价标准可根据以上原则进行设计。

表2 学习质量的目标评价标准

二、模糊评价法概述

(一)模糊集合概述

模糊集合是一种特定的集合，用于描述模糊现象，它不同于普通集合。对于普通集合来说，任何一个元素要么属于要么不属于该集合，非此即彼，界限分明，决无模棱两可，而对于模糊集合来说，一个元素可以既属于又不属于，亦此亦彼，界限模糊。［3］

(二)模糊评价法的原理及方法步骤

模糊评价是基于评价过程的非线性特点而提出的，它是利用模糊数学中的模糊运算法则，对非线性的评价论域进行量化综合，从而得到可以量化的评价结果的过程。［4］

模糊评价法是建立在模糊集合和模糊矩阵的基础之上的，其具体思想如下:

被评对象设定为O，评价指标集:

U={u1，u2，…un}，

指标的权重集:

B={b1，b2，…，bn}，为U上的模糊子集，

评价等级:V={v1，v2，…，vm}，

为各评价等级赋值，构成等级分数集合:

P={p1，p2，…，pm}。

指标Ui在评价等级Vj上的隶属函数:

μR(Ui，Vi)=rij，

其中，R是U×V上的模糊关系，评价矩阵:

R=(rij)，是n×m阶模糊矩阵。

综合评价矩阵:

T=B×R=(t1，t2，…，tm)，由矩阵B和R作矩阵乘法所得。

对T作归一化处理，得到:

T*=(t1*，t2*，…，tm*)，

其中，tj*=tj|(t1+t2+…+tm)(j=1，2，…，m)。

评价等级分数矩阵:P，

令Q=T*×P'，P'是P的转置矩阵，Q为最终的评价结果。

模糊评价法的实施步骤［5］具体由以下八步组成:(1)选定评价对象;(2)建立评价指标体系; (3)确定评价因素权重;(4)确定评价等级录属度;(5)选定模糊算子;(6)建立模糊综合评价数学模型;(7)采集样本数据;(8)进行数据处理得到综合评价结果。

三、模糊评价法在学习质量评价中的应用

(一)确定各项指标权重

评价指标体系中就学习质量的评价分别给出了一级、二级指标以及各项指标的评价标准，但考虑到各个评价指标侧重点有所不同，在评价体系中所处的地位也不一样，因此，必须就各个评价指标赋予各自的权重。针对求权重，通常所用方法有专家打分、德尔菲法以及层次分析法，考虑到这些方法存在主观性较大、不能如实反映各指标的重要程度的问题，同时，为了避免在多个因素间进行比较时人们给出的结果往往不太确定这一情况，本文采用构造模糊一致判断矩阵的方法来解决这一人为因素的影响。

模糊一致判断矩阵R表示在本层次中与之相关的因素之间的重要性的相对比较结果，矩阵可以表示为:

其中，rij表示隶属度，反映的是因素ai与aj之间相比较得到的重要性。当隶属度为0．9时，表示ai相对aj极其重要;当隶属度为0．8时，表示ai相对aj重要很多;当隶属度为0．7时，表示ai相对aj明显重要;当隶属度为0．6时，表示ai相对aj略微重要;当隶属度为0．5时，表示两因素一样重要;当隶属度为0．1～0．4时，两者所处位置的重要性相互交换。

对矩阵中的每一行进行求和，得到h1、h2…hn，则因素ai的权重可以表示为:

根据以上权重确定的方法，经专家比较，得到表1中各指标的权重。

(二)构造模糊评价矩阵

根据评价指标体系和评价标准，邀请包括多类评价主体在内的专家形成多元化评价专家组，对课程体系进行评价。本课题中邀请了20位专家对学习质量进行评价，评价结果如表3所示。

表3 课程体系评价结果

各项指标集合用X={x1，x2，…，xn}表示，评价结果集用Y={y1，y2，…，ym}表示，根据上文所述，评价结果采用五级制，分别用y1、y2、y3、y4、y5表示“优”、“良”、“中”、“合格”、“不合格”。因此，一级指标可以用模糊综合评价矩阵T表示:

根据上述公式，

(三)进行模糊综合评价

1．二级指标模糊综合评价。对因素集进行综合评价，因素集的权重为:

A=［a1a2… an］，

则评价矩阵的值为:

H=A T。

由此可得:

根据最大隶属度原则判断，学习质量评价指标中的学生基础模糊综合评价为“良”。

用同样的方法，可得:

HB=ABTB=［0．1505 0．3645 0．286 0．199 0］。

学习质量评价指标中的学习过程模糊评价为“良”。

Hc=AcTc=［0．318 0．408 0．2 0．052 0］。

学习质量评价指标中的学习效果模糊评价为“良”。

2．一级指标模糊综合评价。

由最大隶属度原则判断得出，学习质量的总体模糊综合评价结果为“良”。

(四)评价结果的处理分析

课题组在对学习质量体系进行模糊综合评价后，认真分析了评价结果，总结了评价主体提出的各种意见，并向专业负责人及专业教师以书面形式进行了反馈。这些将作为专业建设和课程建设与改革的重要依据，也形成教师教学改革的指挥棒，从而最终促进了教学质量的提高。

与传统的专家论证方法相比，模糊理论评价法避免了人为因素的影响，它用定量化的方法保证了评价的客观、公正与合理。其中，评价指标体系的构建、各项指标权重的确定是模糊评价法的关键，这些需要在实施评价前进行反复论证。同时，这也是课题组后续研究工作的主要思路，今后，我们将进一步完善评价指标体系和指标权重。

［1］余向平．高职教育课程考核方式改革的基本思路［J］．职业技术教育，2006(13):52－53．

［2］吕跃进．基于模糊一致矩阵的模糊层次分析法的排序［J］．模糊系统与数学，2002(2):80－81．

［3］李中军．高校教学评估的模糊综合评价模型设计［J］．枣庄学院学报，2009(4):56－57．

［4］于俊乐，许永龙．实践教学课程体系质量的综合评价研究［J］．天津师范大学学报，2010(1):74－77．

［5］朱平．模糊评价法在高职课程体系评价中的应用——以常州机电职业技术学院物联网应用技术专业为例［J］．职业技术教育，2013(5):18－19．

［责任编辑 盛 艳］

2014年度江苏省高校哲学社会科学研究基金资助项目“以学习质量为核心的高职教学质量评价体系研究”(项目编号:2014SJB509);第二期江苏省职业教育教学改革研究课题“工学结合模式下高职院校学生学习质量评价研究”(项目编号:ZYB193);2014年度常州机电职业技术学院课题“高职院校学生学习质量评价体系研究”

刘翠梅，女，常州机电职业技术学院信息工程系讲师，硕士，主要研究方向为电子信息、高等职业教育;顾卫杰，男，常州机电职业技术学院信息工程系副主任，讲师，硕士，主要研究方向为物联网技术、高职教育管理。

G712

A

1674－7747(2015)06－0073－05