粗糙集的过饱和多交叉口协同优化模型研究

陈坚，陈健，邵毅明，邓天民

（1．重庆交通大学山地城市交通系统与安全重庆市重点实验室，重庆400074；2．重庆交通大学交通运输学院，重庆400074；3．中国中铁二院工程集团有限责任公司，四川成都610031）

粗糙集的过饱和多交叉口协同优化模型研究

陈坚1，2，陈健3，邵毅明1，2，邓天民1，2

（1．重庆交通大学山地城市交通系统与安全重庆市重点实验室，重庆400074；2．重庆交通大学交通运输学院，重庆400074；3．中国中铁二院工程集团有限责任公司，四川成都610031）

为解决现有模糊智能控制方法仅适用于单交叉口非饱和状态，满足区域交通过饱和多交叉口信号协同联动控制的需要，提出了高峰时期主通道优化控制策略。在粗糙集知识推理基础上，构建了以多交叉口状态信息为条件属性，以绿灯延长方式、绿灯延长相位和绿灯延长时间3个参数为决策属性的多决策属性模糊控制模型。运用可辨识矩阵与属性频度的属性约简方法对模型进行约简，提取决策规则。实例分析表明：多交叉口主通道绿灯时间延长3～8 s能够有效提高区域交通整体通行效能，同时延长时间不仅与过饱和状态车辆最大排队长度有关，还与绿灯延长方式、绿灯延长相位存在关联，这与交警经验总结的控制规律一致。

交通工程；交通控制；多交叉口；过饱和；粗糙集；决策规则

随着我国社会经济的快速发展及城市化进程的不断加速，城市高度繁荣，但与此同时城市交通拥堵日益严峻，尤其是早晚高峰时期城区常出现大规模交通“瘫痪”。近年来全国城市汽车保有量年均增长15%～20%，有的城市更高达30%，而在有限的城市空间下道路供给资源增长缓慢，交通供需矛盾日益突出。

交叉口信号控制是通过信号相位对交叉口有限通行资源进行时间分配，但如果交叉口流量超过通行能力，则传统的信号控制方法效果不理想，此时交叉口处于过饱和状态。当区域内多个交叉口均处于过饱和状态，则该区域属于多交叉口过饱和。已有研究表明，过饱和多交叉口信号控制与非饱和状态相比，在控制目标排序、多控制目标的优化协调、协调方式的动态变化等有其自身的特点，且常出现车流回溢或相邻车道阻塞导致通行能力降低等现象［1⁃2］。过饱和交叉口的识别可通过高分辨率的交叉口信号数据［3］，主要以最小化交叉口车辆排队长度、均衡路网排队长度或交叉口总交通通行量最大为过饱和交叉口信号控制目标［4⁃6］。控制模型与算法主要有基于交通波理论建立的单交叉口过饱和协调控制模型［7］、离散时间切换系统模型［8］、散波理论与模糊控制相结合的动态相位组合算法［9］。但也有部分研究认为过饱和单交叉口更适合采用多时段定时控制或交警人工指挥效果比信号控制更好［10⁃11］。在过饱和多交叉口方面TONG等［12］以车辆延误最小为目标函数，构建了过饱和交叉口群随机规划模型。雷磊等［13］基于系统工程视角，建立了过饱和的交叉口群控制模型，并设计了该模型的求解算法，实现了交通系统的最优控制。SUN等［14］设计了针对过饱和交叉口群的简化型连续流交叉口方案，实例分析结果表明该方案有90%的概率提升交叉口通行效率。粗糙集是由波兰数学家Z．Pawlak于1982年提出，能够利用不太完整、不太准确的信息，找到适合决策判断的规则，从而进行人工智能决策。虽然发展历史较短，但无论在理论研究还是智能控制、数据挖掘、故障诊断和电力负荷等都取得了丰硕的成果［15］。粗糙集在交通领域的应用还处于起步发展阶段，目前主要体现在区域路网交通信息的提取、交通流拥堵状态的识别、客运量预测等方面［16⁃18］。

已有成果中大多针对交叉口非饱和交通流状态展开，对于饱和与过饱和状态下的交叉口信号控制研究较少，涉及区域过饱和多交叉口的研究成果更为有限，尚未将模糊控制的方法运用于过饱和多交叉口控制中。本文将研究对象拓展为过饱和多交叉口，根据其交通流特性，从区域交通出行OD期望线角度提出了过饱和主通道控制策略，通过多交叉口信号协同控制实现区域大容量快速通道，提高区域交通整体通行效能。并基于粗糙集理论，构建以过饱和交叉口数量、主通道方向车辆最大排队长度、次通道方向车辆最大排队长度等为条件属性，以绿灯延长方式、绿灯延长相位和绿灯延长时间为决策属性的过饱和多交叉口模糊控制模型。

1 粗糙集的基本理论

粗糙集的核心思想是通过寻找等价关系划分论域，假定一个等价关系R，论域U中所有元素可以通过R被分类，从而实现对不可定义的子集近似分类。

1．1 知识与等价类

粗糙集中的知识是将对象进行分类的能力，知识越丰富，对象被划分的更加精细。假定一个知识系统为S＝｛U，A，V，f｝，U为论域，即对象的有限非空集合；A为知识属性的有限非空集合，A＝C∪D，C∩D＝∅，C为条件属性集，D为决策属性集；V为知识属性a∈A的值域；f为对象论域U到知识属性值域V的单映射；同时，一个粗糙集知识系统对应一个粗糙集近似空间Apr＝（U，R）。而决策表是具有U、A、V、f四元组的知识表达系统［19］。

对于知识属性A的任一子集B，存在一个不可分辨的二元关系R（B）。

通过不可分辨关系R（B）可以将知识系统论域U划分为i个互不相交的等价类U／R＝｛X1，X2，…，Xi｝。

1．2 上近似集与下近似集

假设R将论域U划分为若干个基本等价类，X为U的一个子集，x为U的一个对象。如果X可以由基本等价类的并集表示，则X称为U中的精确集。反之，X只有通过近似的方式来表示，称为U中的粗糙集。任何一个不确定集X都可以通过2个精确集（下近似集和上近似集）来刻画。

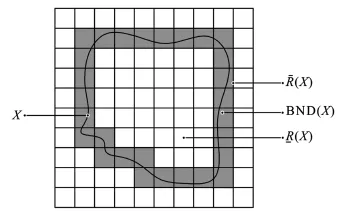
图1 上近似集与下近似集关系图Fig．1 Relation of upper approximation set and lower approximation set

1．3 属性约简

属性约简是粗糙集具体应用的重要步骤，如果知识系统S中，知识属性元素a为不必要属性的充要条件是U／C＝U／（C－｛a｝）。反之，如果U／C≠U／（C－｛a｝），则a为必要属性。因此，粗糙集中的一个属性约简P满足：

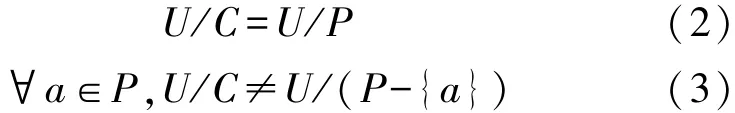
所有约简P构成的集合为red（P），而P中所有必要关系组成的集合为P的核，记为：Core（P）。属性约简剔除了条件属性中的不必要属性，又保证了知识系统分类与决策能力不受影响，其中核是所有属性约简的基础，是知识中最重要部分特征集合，在约简中不能被删除。

2 协同优化模型

2．1 通道划分

过饱和多交叉协同优化模型是通过延长区域某方向绿灯相位时长以打通城市交通出行重要主通道，减少也已经饱和的次通道绿灯相位时长的控制策略。其中，主通道方向是整个城市交通出行主要OD期望线在该区域的通过方向，具体计算可通过各交叉口进口道交通流量进行OD反推，次通道则为交叉口与主通道相交的其他进口道方向。主通道控制策略是将交叉口时间资源向某一方向通行倾斜，从而激活区域交通关键方向通路，实现区域整体交通的畅通。主通道控制策略不同于干道绿波带，绿波带是从通行速度的角度对交叉口信号配时进行优化，而主通道策略是以区域交通整体效能（效率与能力）最大化为目标进行信号控制。

2．2 属性选择

模型以过饱和交叉口数量、各交叉口主次通道最大车辆排队长度为条件属性，分别以绿灯延长方式、绿灯延长相位和绿灯延长时间为决策属性，从而构建同一条件属性不同决策属性的3个决策表。模型不采用高峰时间交叉口各进口道流量之和作为条件属性，是考虑各交叉口进口道通行能力不一致，如果单纯以进口道流量为条件属性将导致信号控制失实。交叉口主、次通道最大车辆排队长度分别如式（4）～（5）所示：

式中：区域内过饱和交叉口总数量为N；qzni为第n个交叉口主通道方向红灯时段内第i个车道的车辆排队长度，0≤i≤I；qcnj为第n个交叉口次通道方向红灯时段内第j个车道的车辆排队长度，0≤j≤J。

决策属性值的确定是以条件属性值为基础参数，以区域多交叉口总延误最小为目标函数，在Syn⁃chro平台多次仿真比较从而确定的最优值。所构建的协同优化控制模型重要作用在于从每一行条件属性数据仿真得到一次最优值的繁琐计算或是交警人工经验决策的基础上，通过粗糙集工具提取抽象决策规则，从而为不同城市不同区域的多交叉口过饱和智能控制提供决策建议。

2．3 属性值模糊化

为避免属性值的连续性，将第n个交叉口主、次通道方向上最大排队长度qzn和qcn的属性值不再采用其实际排队长度值，而是通过线性分布的隶属函数进行模糊化处理，在qzn和qcn的论域上定义7个模糊语言子集｛很短VS，短S，较短RS，一般M，较长RL，长L，很长VL｝，所对应的属性值为｛0，1，2，3，4，5，6｝。

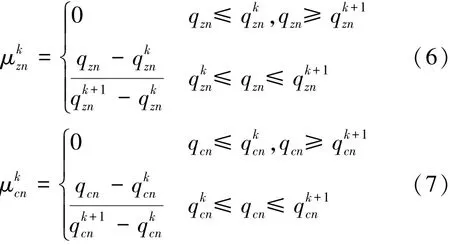
分别将qzn和qcn的多组实际数据的最大值和最小值，按等步长离散为7级，记为和则qzn和qcn对属于第k级的隶属度计算方法如式（6）、（7）所示［20］，最大隶属度所对应的级别为qzn和qcn属性值。式中：qzn为第n个交叉口主通道方向的实际最大排队长度，qcn第n个交叉口次通道方向的实际最大排队长度，为qzn属于第k级的隶属度，为qcn属于第k级的隶属度，为主通道方向第k级的上限值，为次通道方向第k级的上限值。

条件属性中交叉口数量已经为离散型数据，则以实际整数值为N的属性值，如：区域内过饱和交叉口数量为1，则N＝1。

决策属性中绿灯延长方式W是指哪些交叉口主通道方向绿灯时间延长，根据区域交叉口交通控制实际情况，模型中绿灯延长方式定义为过饱和交叉口主通道方向绿灯时长延长和所有交叉口主通道方向绿灯时长都延长2种情况，属性值分别对应为W＝0，W＝1。绿灯延长相位E是指交叉口主通道方向哪些相位绿灯时间延长，定义绿灯延长相位取值E＝0，指主通道直行相位绿灯时间延长，次通道左转相位绿灯时间减少；E＝1，指主通道直行和左转相位绿灯时间都延长，次通道直行和左转相位绿灯时间减少。绿灯延长时间G属性值为延长时间的实际值。

2．4 决策表构建与属性约简

2．4．1 决策表构建

将条件属性与决策属性数据采集并进行相应模糊化处理，从而形成含有2N＋1个条件属性、3个决策属性的多交叉口过饱和优化控制决策表，由于3个决策属性无法同时约简，需要一一约简，实则相当于3个决策表。

2．4．2 基于可辨识矩阵与属性频度的属性约简

假设1个决策表T＝（U，C∪D），｜U｜＝n，决策表T所对应的可辨识矩阵为M＝（Cij）n×n，其中：并且从条件属性集合C中删除B中元素，C＝C－B。

5）计算条件属性集合C中剩余的所有元素在可辨识矩阵M中出现的次数p（c），将最大次数所对应的元素添加入约简属性集合B中，B＝B＋cq，p（cq）＝max｛p（c）｝。

6）如果M＝∅，则输出约简集合B；否则，返回3）。

2．4．3 规则提取

根据约简集合B中的条件属性元素构成及所

可辨识矩阵是关于对角线对称的矩阵，且对角线元素均为0。当论域U中的2个元素xi和xj所对应的决策属性值相同时，可辨识矩阵中元素取0；反之，可辨识矩阵中元素取值为二者条件属性中的不同值。同时，通过条件属性a在可辨识矩阵M出现的次数p（a）以表征属性a的重要程度，p（a）＝SGF（a，R，D）。

基于可辨识矩阵与属性频度的属性约简的算法思想是将决策表转化为可辨识矩阵，以获得所有非核条件属性在可辨识矩阵出现的次数，从而将次数最大的非核条件属性纳入约简集合中，删除包含该属性的所有属性组合［21⁃22］。具体算法步骤如下：

1）如果决策表中的条件属性值与决策属性值存在连续变量，则进行离散化处理。属性约简集合B＝∅，Core＝∅。

2）根据决策表与式（8）生成可辨识矩阵M。

3）找出可辨识矩阵的核集合Core（属性组合数为1），并更新约简集合B＝Core。

4）删除可辨识矩阵中与B交集不为空的元素，对应的决策属性，提取多交叉口过饱和优化控制决策规则。

2．5 评价指标计算

规则提取后的评价指标计算是检验规则准确、信息涵盖量的重要依据，采用规则支持度、精确度和覆盖度3个指标进行衡量。具体指标为［20］

式中：｜·｜表示集合中的元素个数，该元素是指论域中的数据项即决策表中的一行。将评价指标中精度低于50%的规则剔除，以保证规则的有效性。

3 实例分析

以重庆市江北区新南路4个连续交叉口为实例分析对象，新南路位于重庆市北环高速以南，是贯穿江北区东西方向的重要主干道，周边分布有大型住宅、商业和办公等多种业态。其中，交叉口4为新南路与星光大道交叉口，星光大道是江北区南北方向主干道，早晚高峰时期，新南路该4个交叉口均处于过饱和状态。交叉口的地理分布如图2所示，Syn⁃chro软件中仿真图如图3所示，由于重庆市江北区主要交通出行OD期望线为东西方向，因此确定新南路为主通道方向，与之垂直的各道路方向为次通道方向。

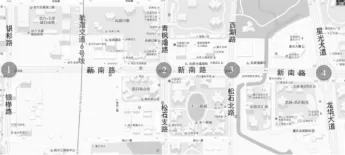
图2 重庆市江北区新南路4个交叉口地理分布Fig．2 Geographical distribution of four intersections in Xinnan road，Jiangbei district，Chongqing

图3 新南路交叉口仿真建模Fig．3 Simulation modeling of Xinnan road intersec⁃tions

通过多天晚高峰交叉口实际数据连续调查，并根据式（4）～（7）得到4个交叉口过饱和优化控制的10种情景条件属性值。将各种情景中的交叉口进口道流量数据输入Synchro仿真软件，优化得出信号配时方案。人工多次实验调整交叉口主通道方向绿灯延长方式、绿灯延长相位及绿灯延长时间，当总延误时长指标最优时，该次实验参数值即为决策属性值，具体决策表如表1所示。

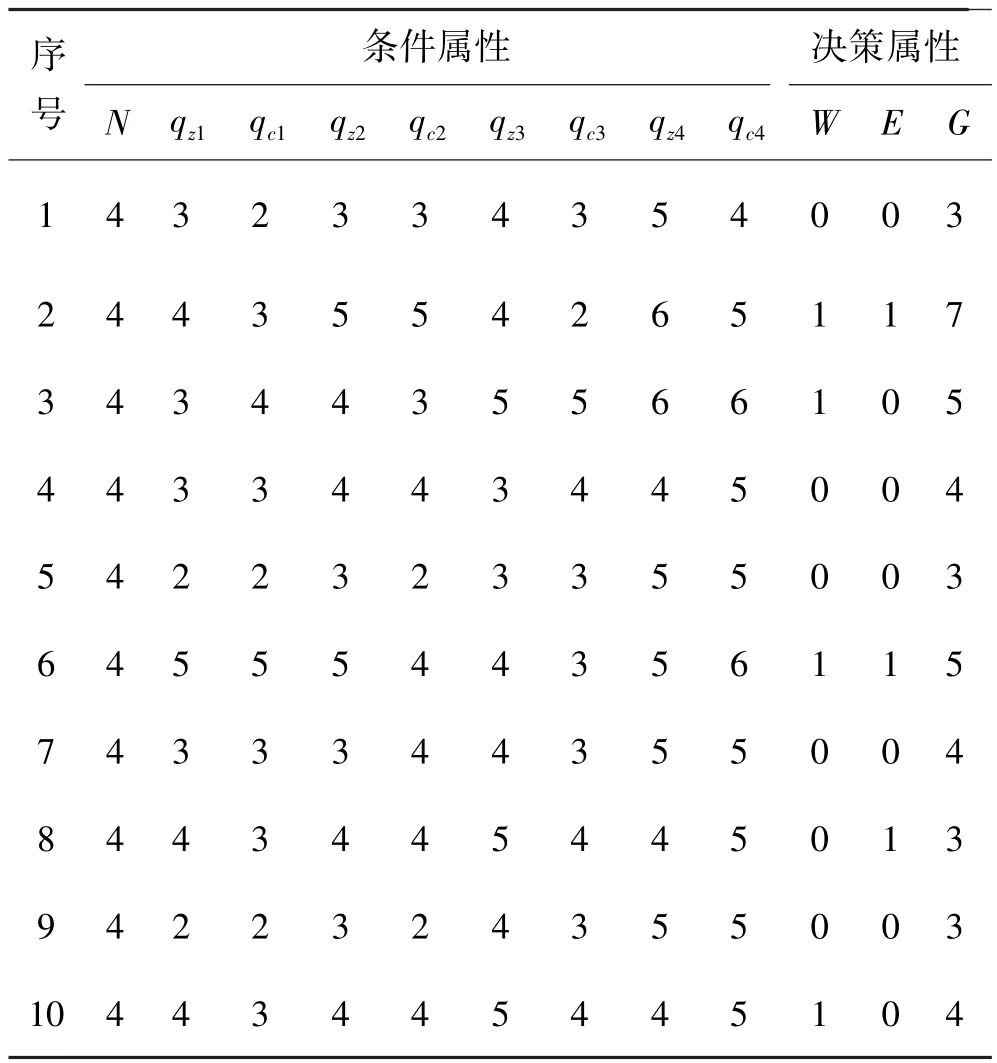
表1 多交叉口过饱和优化控制决策表Table 1 Optimization control decision of oversaturated multi⁃intersection

以W为决策属性，根据决策表约简算法，得到约简集合为｛qz2，qz3，qz4｝。将相同决策规则合并，并通过式（9）～（11）计算各决策规则评价指标值如表2所示。

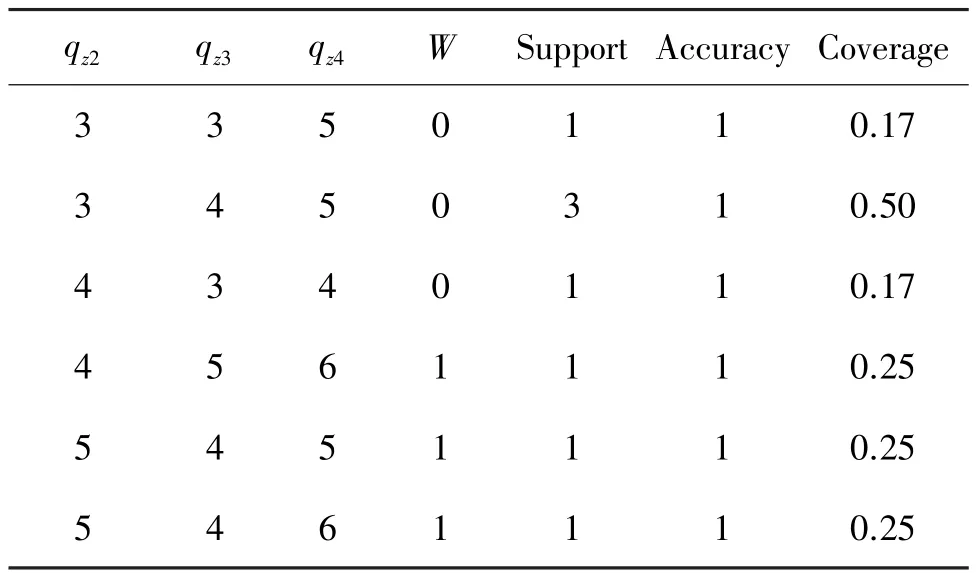
表2 以W为决策属性的决策表约简结果Table 2 Reduction result of decision table on W as decision attribute

同理，以E为决策属性，得到约简集合为｛qz1，qz4｝。将相同决策规则合并，最终约简结果如表3所示。

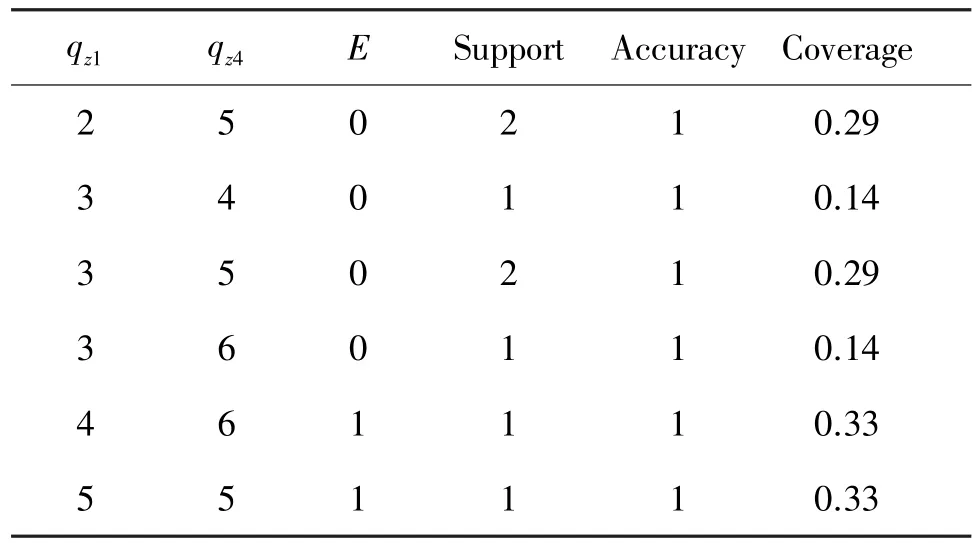
表3 以E为决策属性的决策表约简结果Table 3 Reduction result of decision table on E as decision attribute

以G为决策属性，得到约简集合为｛qc1，qz3，qz4｝。将相同决策规则合并，最终约简结果如表4所示。

表4 以G为决策属性的决策表约简结果Table 4 Reduction result of decision table on G as decision attribute

根据3组决策表约简结果提取得出4个过饱和交叉口的模糊控制决策规则如表5所示。

表5 模糊控制决策规则Table 5 Fuzzy control decision rules

对表5的模糊决策规则进行分析讨论：1）当交叉口1、2、3主通道方向排队长度级别为一般（M）以上时，交叉口绿灯信号延长的方式可以从仅过饱和交叉口主通道方向绿灯时间延长扩展到与过饱和交叉口相邻的其它交叉口相同方向绿灯时间也相应延长；绿灯延长相位也可从延长主通道直行相位绿灯时间、减少次通道左转相位绿灯时间扩展到主通道直行与左转相位绿灯时间都延长、次通道直行和左转相位绿灯时间减少的控制策略，这进一步丰富和完善了文献［10］的研究结论。2）交叉口主通道方向绿灯时间延长的具体数值在3～8 s为宜，具体数值与饱和度最高的交叉口3、4主通道方向排队长度紧密相关，也与交叉口1的次通道方向排队长度有直接关系。同时，绿灯延长时间还与绿灯延长方式、绿灯延长相位2个决策属性存在关联性，表现为W、E为0时，绿灯相位延长时间较短，W、E为1时，绿灯相位延长时间较长；交叉口主通道方向排队长度越长，绿灯相位延长时间越长的模糊控制规律。

4 结束语

过饱和多交叉口协同优化模型具有信息量大、复杂性高和随机性强等特点，传统确定性优化模型效果有限。虽然国内外近年来运用模糊控制方法对单个过饱和交叉口进行了大量研究，但过饱和多交叉口智能信号控制不是简单的单个模糊控制模型叠加，应从区域过饱和多交叉口系统协同优化角度研究。本文在分析过饱和多交叉口智能控制特点的基础上，提出了主通道控制策略以实现过饱和多交叉口间决策关联，从而提高区域整体通行效能。并根据区域交叉口控制的实际情况构建以过饱和交叉口数量、主次通道排队长度为条件属性，以绿灯延长方式、绿灯延长相位和绿灯延长时间为决策属性的粗糙集模糊控制模型，运用可辨识矩阵与属性频度的属性约简方法分别以相同条件属性、不同决策属性对3组粗糙集进行约简，提取决策规则并计算评价指标。

根据重庆市新南路4个过饱和交叉口的实例分析，总结了过饱和多交叉口控制的基本规律，研究结论不仅可以为交警在早晚高峰时期区域大面积过饱和交通状态下指挥交通提供决策参考，也可为大城市高峰时期区域交通协同联动控制提供新的思路。但多决策属性间的关联性对粗糙集属性约简的影响及多决策属性的一次性约简算法还有待进一步研究，决策属性的具体取值还有改进空间。

［1］CHEN Shuiyu，XU Hao，LIU Hongchao．Timing oversatu⁃rated signals：what can we learn from classic and state－ofthe－art signal control models［J］．Journal of Transportation Systems Engineering and Information Technology，2013，13（1）：97⁃110．

［2］李瑞敏．过饱和交叉口交通信号控制研究现状与展望［J］．交通运输工程学报，2013，13（6）：119⁃126．LI Ruimin．Study status and prospect of traffic signal control for over⁃saturated intersection［J］．Journal of Traffic and Transportation Engineering，2013，13（6）：119⁃126．

［3］WU Xinkai，LIU H X，GETTMAN D．Identification of over⁃saturated intersections using high⁃resolution traffic signal da⁃ta［J］．Transportation Research Part C：Emerging Technolo⁃gies，2010，18（4）：626⁃638．

［4］ABOUDOLAS K，PAPAGEORGIOU M，KOUVELAS A，et al．A rolling⁃horizon quadratic⁃programming approach to the signal control problem in large⁃scale congested urban road networks［J］．Transportation Research Part C：Emerging Technologies，2010，18（5）：680⁃694．

［5］李岩，赵志宏，李鹏飞，等．过饱和状态交通信号控制方法综述［J］．交通运输工程学报，2013，13（4）：116⁃126．LI Yan，ZHAO Zhihong，LI Pengfei，et al．Review of traffic signal control methods under over⁃saturated conditions［J］．Journal of Traffic and Transportation Engineering，2013，13（4）：116⁃126．

［6］LIU Hongchao，BALKE K N，LIN Weihua．A reverse caus⁃al⁃effect modeling approach for signal control of an oversatu⁃rated intersection［J］．Transportation Research Part C：E⁃merging Technologies，2008，16（6）：742⁃754．

［7］WU Aoxiang，QI Liqun，YANG Xiaoguang．Mechanism a⁃nalysis and optimization of signalized intersection coordina⁃ted control under oversaturated status［J］．Procedia⁃Social and Behavioral Sciences，2013，96：1433⁃1442．

［8］向伟铭，肖建，蒋阳升．基于切换系统的过饱和信号交叉口混杂控制［J］．交通运输系统工程与信息，2014，14（2）：57⁃61．XIANG Weiming，XIAO Jian，JIANG Yangsheng．Hybrid control for over⁃saturated signalized intersection based on switched system［J］．Journal of Transportation Systems Engi⁃neering and Information Technology，2014，14（2）：57⁃61．

［9］陈智，刘小明，刘文婷，等．过饱和交叉口交通信号模糊关联控制方法［J］．信息与技术，2014，43（3）：374⁃380．CHEN Zhi，LIU Xiaoming，LIU Wenting，et al．Intercon⁃nected control of traffic signals at oversaturated intersections using fuzzy control method［J］．Information and Control，2014，43（3）：374⁃380．

［10］杨立才，贾磊，赵建玉，等．基于粗集理论的交通控制系统研究［J］．中国公路学报，2005，18（2）：79⁃83．YANG Licai，JIA Lei，ZHAO Jianyu，et al．Study of traf⁃fic control systems based on rough sets theory［J］．China Journal of Highway and Transport，2005，18（2）：79⁃83．

［11］于泉，荣建．基于模糊逻辑的过饱和交叉口定周期配时方案优化［J］．北京工业大学学报，2007，33（11）：1173⁃1176．YU Quan，RONG Jian．Fixed timing plan optimization for oversaturated intersection based on fuzzy logic［J］．Journal of Beijing University of Technology，2007，33（11）：1173⁃1176．

［12］TONG Yue，ZHAO Lei，LI Li，et al．Stochastic program⁃ming model for oversaturated intersection signal timing［J］．Transportation Research Part C：Emerging Technologies，2015，58，474⁃486．

［13］雷磊，吴洋，刘昱岗．过饱和交叉口群系统建模及优化模型［J］．计算机工程与应用，2010，46（4）：26⁃28．LEI Lei，WU Yang，LIU Yugang．System modeling and optimization model of oversaturated intersection group［J］．Computer Engineering and Applications，2010，46（4）：26⁃28．

［14］SUN Weili，WU Xinkai，WANG Yunping，et al．A contin⁃uous⁃flow⁃intersection⁃lite design and traffic control for oversaturated bottleneck intersections［J］．Transportation Research Part C：Emerging Technologies，2015，56：18⁃33．

［15］PAI Pingfeng，CHEN Taichi．Rough set theory with dis⁃criminant analysis in analyzing electricity loads［J］．Expert Systems with Applications，2009，36（5）：8799⁃8806．

［16］戢晓峰，刘澜，吴其刚．区域路网交通信息提取方法［J］．西南交通大学学报，2008，43（3）：422⁃426．JI Xiaofeng，LIU Lan，WU Qigang．Extraction method for traffic information of regional road network［J］．Journal of Southwest Jiaotong University，2008，43（3）：422⁃426．

［17］蒲世林，李瑞敏，史其信．基于粗糙集⁃模糊识别技术的交通流状态识别算法研究［J］．武汉理工大学学报：交通科学与工程版，2010，34（6）：1154⁃1158．PU Shilin，LI Ruimin，SHI Qixin．Study on auto⁃identifi⁃cation algorithm of traffic flow state based on rough set and fuzzy theory［J］．Journal of Wuhan University of Technolo⁃gy：Transportation Science＆Engineering，2010，34（6）：1154⁃1158．

［18］陈坚，霍娅敏，傅志妍，等．基于粗糙集的公路客运量预测［J］．重庆交通大学学报：自然科学版，2009，28（6）：1071⁃1074．CHEN Jian，HUO Yamin，FU Zhiyan，et al．Forecast of highway passenger transport volume based on rough set the⁃ory［J］．Journal of Chongqing Jiaotong University：Natural Science，2009，28（6）：1071⁃1074．

［19］王国胤，姚一豫，于洪．粗糙集理论与应用研究综述［J］．计算机学报，2009，32（7）：1229⁃1246． WANG Guoyin，YAO Yiyu，YU Hong．A survey on rough set theory and applications［J］．Chinese Journal of Comput⁃ers，2009，32（7）：1229⁃1246．

［20］霍娅敏，陈坚，李啸虎，等．城市建设项目交通影响后评价模型［J］．交通运输工程学报，2012，12（1）：79⁃86．HUO Yamin，CHEN Jian，LI Xiaohu，et al．Traffic impact post⁃evaluation model of urban construction project［J］．Journal of Traffic and Transportation Engineering，2012，12（1）：79⁃86．

［21］任小康，吴尚智，马如云．基于可辨识矩阵的属性频率约简算法［J］．兰州大学学报：自然科学版，2007，43（1）：138⁃140．REN Xiaokang，WU Shangzhi，MA Ruyun．An algorithm of attribute frequency reduction based on discernibility ma⁃trix［J］．Journal of Lanzhou University：Natural Science，2007，43（1）：138⁃140．

［22］欧芳芳，马晓辉，马利芳，等．基于改进属性频度的属性约简算法［J］．电力科学与工程，2009，25（5）：60⁃63．OU Fangfang，MA Xiaohui，MA Lifang，et al．One im⁃proved algorithm of attribute reduction based on frequency of attributes［J］．Electric Power Science and Engineering，2009，25（5）：60⁃63．

Collaborative optimization model for oversaturated multiple intersections based on the rough set theory

CHEN Jian1，2，CHEN Jian3，SHAO Yiming1，2，DENG Tianmin1，2

（1．Chongqing Key Lab of Traffic System＆Safety in Mountain Cities，Chongqing Jiaotong University，Chongqing 400074，China；2．School of Traffic and Transportation，Chongqing Jiaotong University，Chongqing 400074，China；3．China Railway Eryuan Engineer⁃ing Group Co．，Ltd，Chengdu 610031，China）

To solve the defect that the existing fuzzy intelligent control method is only suitable for a single intersec⁃tion under unsaturated state，and to meet the need of coordination control of regional traffic for oversaturated multi⁃ple intersections，an optimization control strategy for main channel at peak time was proposed．The fuzzy control model with multiple decision attributes was established on the basis of knowledge reasoning in rough sets theory．It took multiple intersections state information as condition attributes，and the elongation mode，phase，and green light timing，as decision attributes．The methods of attribute reduction of the discernibility matrix and the frequency of attribute were used in the model，then some decision rules were extracted．The results show that the efficiency of regional traffic was improved via 3⁃8 more seconds of green light signal at the main channel．In addition，the exten⁃sion time is not only related to the maximum queue length of vehicles under oversaturated vehicle conditions，but also the extension mode and phase of green light，which is consistent with the experience of traffic police．

traffic engineering；traffic control；multiple intersections；oversaturated；rough set theory；decision rule

陈坚，男，1985年生，副教授，主要研究方向为交通行为理论与实证、运输系统分析与决策。曾获四川省科技进步三等奖1项，广西发改委优秀成果二等奖1项，发表学术论文30余篇，其中被EI检索11篇。

陈健，男，1976年生，高级工程师，主要研究方向为智能交通、交通规划。参加各类项目100余项，担任近50余个项目专业设计负责人，获得四川省及集团公司优秀工程咨询一等奖1项、二等奖2项、三等奖5项。

邵毅明，男，1955年生，教授，博士生导师，主要研究方向为道路交通安全、智能交通。曾获上海市科技进步一等奖1项，重庆市科技进步二等奖1项、三等奖2项，重庆市政府发展贡献三等奖1项，中国智能交通协会科学技术三等奖1项，发表学术论文100余篇。

U491．54

A

1673⁃4785（2015）05⁃0783⁃07

10．11992／tis．201406045

http：／／www．cnki．net／kcms／detail／23．1538．tp．201509030．1456．002．html

陈坚，陈健，邵毅明，等．粗糙集的过饱和多交叉口协同优化模型［J］．智能系统学报，2015，10（5）：783⁃789．

英文引用格式：CHEN Jian，CHEN Jian，SHAO Yiming，et al．Collaborative optimization model for oversaturated multiple inter⁃sections based on the rough set theory［J］．CAAI Transactions on Intelligent Systems，2015，10（5）：783⁃789．

2014⁃06⁃22．

日期：2015⁃09⁃30．

科技部“863”计划资助项目（2011AA110306）；国家自然科学基金资助项目（51308569）；中国中铁二院工程集团有限责任公司科研资助项目（2014⁃50）．

邵毅明．E⁃mail：sym＠cqjtu．edu．cn．