单箱多室箱梁横向内力计算方法探析

赵原

(锦州铁道勘察设计院有限公司,辽宁锦州 121000)

单箱多室箱梁横向内力计算方法探析

赵原

(锦州铁道勘察设计院有限公司,辽宁锦州 121000)

单箱多室箱梁的横向内力计算还没有明确的简化计算方法。本文通过对多室箱梁横向计算时不同支承边界的分析探讨,来确定一个满足计算精度要求的边界条件,从而为建立多室箱梁的分析模型提供一个简化计算方法。

单箱多室 横向计算 弹性支承

随着社会经济的发展和桥梁工程技术的进步，宽高比较大的混凝土箱梁在桥梁工程中应用的越来越广泛，箱室数量也越来越多。在一般的箱梁设计中，箱梁的纵向受力分析设计通过采用平面杆系有限元程序，得到了较好的解决，而箱梁横向受力分析，目前还缺乏行之有效的简化分析方法。由于横向设计上的不合理，特别是单箱多室箱梁，导致许多的箱梁桥在运营过程中出现了纵向裂缝，损害了桥梁的安全性及耐久性。

目前对于箱梁横向内力的计算方法，主要包括：影响面法，有效宽度法，TY框架分析法，刚性支承L框架法及实体有限元法。影响面法及有效宽度法忽略了腹板的弹性约束的影响；TY框架分析法是美国《预制节段箱形梁手册》推荐方法，有严格的理论推导，但只适用于单箱单室截面；刚性支承框架法，由于对剪力支承边界模拟上的不合理，导致实际的计算偏差较大，结果往往偏不安全。实体有限元法能够精确的计算箱梁横向内力，但实际使用时建模工作量大且不易修改，最不利布载及结果提取不方便，因而在常规设计中使用较少。

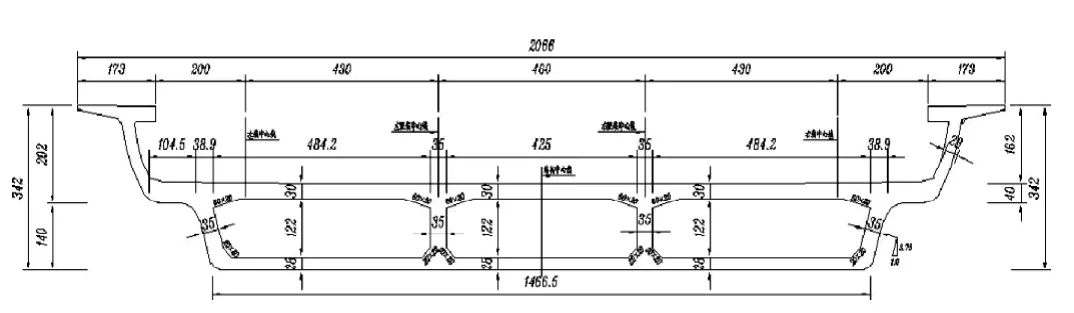
图1 箱梁跨中横断面(单位:cm)

图2 横向框架计算模型

随着桥梁设计的进步，对于多室箱梁，部分设计者采用了弹性支承框架法来简化分析截面横向内力，取得了较好的效果。弹性支承能够反映箱梁的纵向支承特性，其结果的精度取决于支承弹簧刚度的取值的合理与否，本文通过对不同刚度支承下的横向模型进行分析对比，探讨单箱多室箱梁横向内力的简易计算方法。

1 工程实例

x市地铁6号线部分区段采用高架形式，某处桥梁结构采用7-35m预应力混凝土连续梁，为四线桥，线间距分别为4．3+4．6 +4．3m，采用单箱三室等高度斜腹板箱形截面，梁高为1．8m，结构底宽14．665m，顶宽20．66m，跨中处腹板厚度35cm，底板厚28cm，顶板厚30cm，箱梁跨中处的横断面见图1。

2 横向计算方法

预应力混凝土连续箱梁是个空间结构，本设计分析时将箱梁计算的空间问题转化为平面问题，在连续梁纵向计算通过后，需计算横向能否通过。

横向计算方法：将箱梁横断面模拟为横向框架结构，在纵向取最不利断面中的一延米对其进行受力分析。离中支点越近，箱梁截面越大，刚度越大，故箱梁截面最小的是连续梁跨中附近截面，即图1所示截面作为计算截面。箱梁横截面可作为支承在箱梁腹板中心线下缘的框架结构，然后对横向框架进行有限元分析，框架截面划分为120个节点和42个单元，结构计算模型见图2。

横向框架采用Midas civil程序按照不同荷载组合进行计算分析，并根据规范对其进行验算。

3 横向框架计算及结果分析

对于箱梁结构，一般假定由结构腹板来承担结构剪力，对单箱单室对称结构来说，采用腹板下的固定加滑动支座的模型计算就可以满足计算精度的要求，但对多室箱梁来说，内外腹板由于结构截面的差异，承受的剪力大小及变形也不一致，若采用固定支承，则可能限制了部分节点的竖向变形，而使结构内力分析与实际情况有较大的差别。

表1

表2

本文主要通过在恒载及列车荷载下不同支承情况下箱梁顶板内力比较分析，探索选取适宜的结构边界模拟条件，来简化结构内力分析计算方法，提高结构内力分析精度。

本次分别采用以下边界条件结算结构内力：

边界1：腹板下节点均采用一般支承(竖向支座固定)

边界2：腹板下节点均采用节点弹性支承

(竖向支座弹性刚度分别为：1+1+1+1)

边界3：腹板下节点均采用节点弹性支承

(竖向支座弹性刚度分别为：1．1+0．9+0．9+1．1)

边界4：腹板下节点均采用节点弹性支承

(竖向支座弹性刚度分别为：0．9+1．1+1．1+0．9)

边界5：腹板下节点均采用节点弹性支承

(竖向支座弹性刚度分别为：0．5+0．5+0．5+0．5)

边界6：腹板下节点均采用节点弹性支承

(竖向支座弹性刚度分别为：0．75+0．75+0．75+0．75)

边界7：腹板下节点均采用节点弹性支承

(竖向支座弹性刚度分别为：2+2+2+2)

(整体刚度按简支梁跨中截面处简化计算

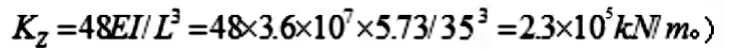
以上刚度均为假定单位刚度Ki=Kz/4=5．75x104kN/m。

不同边界条件下内力比较表1：

不同边界条件下内力比较表2：

表1的结果为整体支承刚度一定条件下(内外腹板支承刚度分配比例变化)与固定支承条件下的内力比较。从结果可知，边孔顶板内力结果差异性较大，而中孔顶板内力结果差异性较小。

表2的结果为弹性支承条件下各个腹板支承刚度大小一致，而总体支承刚度变化条件下的内力比较。从结果可知，边孔顶板边角点内力结果几乎无变化，中孔结构顶板内力结果差异性较小，边孔顶板跨中及内侧角点内力差异性较大。具体来说则是顶板结构的内力均随着整体支承刚度的减小而增加(边孔边角点除外)。

通过笔者的进一步分析比较，随着整体刚度增大到一定限值(3倍的假定单位刚度)，边孔边角点的内力结果则开始增加，随着整体刚度的继续增加，内力结果则向一般支承条件下内力结果靠近，直至一致。

4 结语

本文通过对多室箱梁横向内力计算时不同支承条件下的结果分析，得出以下结论：

(1)对多室箱梁横向计算来说，不同支承条件下，箱梁部分节点的内力计算结果差异性较大，说明选择合理的结构的边界支承条件对结构计算至关重要。

(2)相对来说，以弹性支承框架法来计算多室箱梁的内力，与实际结构的边界条件较为接近，具有较高的精度。

(3)在弹性支承条件下，适当地降低支承的刚度，计算结果是偏安全的，有利于提高结构的安全系数。

为进一步对多室箱梁的边界支承条件问题的研究，可以沿着以下几个方向展开：

(1)研究不同支承刚度对横向内力计算的影响，进行敏感性分析，以降低对弹簧刚度计算的精度要求，简化分析计算方法。

(2)研究不同截面参数对弹簧刚度识别结果的影响，得到等效弹簧支承刚度的经验或者理论计算公式，推动弹性支承框架法在工程计算中的应用。

(3)研究多室箱梁多个腹板的弹性支承刚度的合理分配问题，得到经验或者理论计算方法，使结构计算更加合理安全。

(4)进一步研究弹性支承位置的合理设置，更加真实的模拟结构的实际边界情况。

[1]《铁路桥涵钢筋混凝土和预应力混凝土结构设计规范》(TB1000 2.3-2005).

[2]郭金琼,房贞政,郑振.箱形梁设计理论[M].人民交通出版社,2008.10.