技术进步偏向对制造业就业增长的影响

摘要:基于要素增强型生产函数构建技术进步偏向对就业增长影响的理论模型,并利用1987—2013年中国制造业数据进行实证检验,分析表明:制造业部门中资本与劳动之间呈互补关系;1987—2013年整个制造业的技术进步是偏向资本的,并且其各行业的技术进步也基本偏向资本;技术进步偏向资本对整个制造业就业增长具有抑制作用,但与1987—1999年相比,2000—2013年技术进步偏向对就业增长的影响明显下降;大多数制造业行业的技术进步具有较强的资本替代劳动特征,其中劳动密集型行业技术进步对劳动的替代较小,而工资上涨进一步诱导行业技术进步偏向资本。为保障就业稳定增长,应加强对前沿技术引进的宏观调控和管理,降低资本替代劳动的速度,实现技术进步与就业增长的良性互动。
关键词:制造业;技术进步偏向;就业增长;要素替代;资本替代劳动;要素报酬;劳动密集型行业;资本密集型行业;技术密集型行业;工资上涨
中图分类号:F062.4;F224.0 文献标志码:A文章编号:16748131(2015)06006208
一、引言
长期以来,技术进步与就业增长的关系是经济学界重要的研究领域。技术进步是创造了更多的就业机会,还是导致失业率的提升?针对这一问题的回答并不确定,因为即使同一国在同一经济环境的不同发展阶段也有很大的差异。Aghion et al(1994)认为技术进步对就业的影响具有双重性:一方面资本深化过程提高了资本收益,增加劳动力的需求而促进就业增长;另一方面技术创新的破坏效应缩短了劳动力的工作匹配周期,减少工作岗位而抑制就业增长。Cyert et al(1987)指出,在美国工业化进程中,前沿技术进步通过提高劳动生产效率减少劳动力需求;同时,它又会提高要素生产率而降低产品价格,引起产出需求的增加,进而扩大对劳动的需求;因此,只有在技术进步的就业增长效应大于替代效应时才会促进社会就业总量的增加。王林辉等(2011)和朱翠华等(2012)认为我国技术进步的就业增长效应是高于替代效应的,表现出就业总量的增加。而朱轶等(2009)在利用DEA方法估算全要素生产率基础上,研究了我国技术进步、产业结构对就业的影响,发现二、三产业的技术进步并没有对整体就业产生促进作用,尤其是服务业的技术进步产生了负面的就业影响。
纵观国内外研究成果,现有研究大都在广义技术进步下分析就业效应问题,但是这不能反映前沿技术进步的方向对就业增长的影响。因为随着高新技术的快速发展和先进技术、设备的引进,市场对技能劳动力需求增加,同时技能劳动力的收益增多,技术进步偏向资本如果技术进步更有助于提高某种要素的边际产出,称之为偏向该要素的技术进步,或说技术进步偏向该要素。 的同时也偏向技能劳动力,这种趋势愈来明显,即技术进步、资本和技能劳动融合发展(Antras,2004;Klump,2007;Sato et al,2009;Acemoglu,2010)。具体而言,在经济发展过程中,技术进步体现在资本和机器设备投入中,并且技术进步收益率也体现在资本收益中,即旧资本的技术水平远不如新资本。这意味下降的资本设备价格会产生两方面的影响:一是引起发展中国家对发达国家机器设备的需求增加,二是发达国家增加对新设备投入再生产。这使得无论是发达国家还是发展中国家对技能劳动力的需求都会增加,进而提升劳动力就业结构,并最终影响就业总量。
本文根据我国技术进步及经济发展的特性,基于要素增强型生产函数,构建技术进步偏向对就业增长影响的理论框架,尝试从技术进步偏向角度分析就业问题。技术进步偏向将有利于某些生产要素,但有可能降低其他要素报酬。换句话说,技术进步的方向直接决定了经济发展过程中劳动力规模和结构需求的变化。由于制造业作为经济社会发展的基础性产业,是吸纳我国庞大劳动力大军的重要部门之一,因此,本文选取1987—2013年中国制造业数据实证分析技术进步偏向对其就业增长的影响,并就实证结果提出有助于我国就业持续稳定增长的技术发展政策。
钟世川:技术进步偏向对制造业就业增长的影响
二、理论模型
本文采用要素增强型生产函数进行模型构建,具体的生产函数形式如下:
Yt=[θ(AtKt)-1-σσ+(1-θ)(BtLt)-1-σσ]-σ1-σ(1)
其中,Yt为产出,Kt为资本投入,Lt为劳动投入,At为资本增强型技术进步指数,Bt为劳动增强型技术进步指数;θ∈(0,1)是反映生产过程中资本要素和劳动要素之间的重要性分配参数,σ∈(0,∞)为资本与劳动之间的替代弹性。
在规模报酬不变时,利用厂商利润最大化的一阶条件可得资本边际产出等于资本报酬率rt,劳动边际产出等于劳动报酬率wt,即:
FKFL=θ1-θ(AtBt)σ-1σ(LtKt)1σ=rtwt(2)
将(2)式两边取对数,有:
lnrtwt=lnθ1-θ+σ-1σ(lnAt-lnBt)+1σ(lnLt-lnKt)(3)
根据Acmoglu(2002,2003,2010)和钟世川(2014)对技术进步偏向的定义可知,(3)式右边第二项便是技术进步偏向Dt的表达式:
Dt=σ-1σ(lnAt-lnBt)(4)
由技术进步偏向的定义可知,(4)式的经济学含义是:技术进步引起资本与劳动之间的边际产出比的变化率。由(4)式可知,要素替代弹性的大小决定了技术进步偏向性。当要素替代弹性σ>1时(资本与劳动之间是替代的),若lnAt>lnBt(lnAtlnBt(lnAt
根据(4)式可知,要测算各行业的技术进步偏向性,需要先估算要素替代弹性,本文沿用钟世川(2014)所采用的标准化系统方法,在(1)式下,资本和劳动按其边际产出获得报酬。结合(1)式,可得到一个方程组,并将各变量的样本均值对其自身变量进行标准化。具体过程如下:
根据(1)式,资本和劳动按其边际产出获得报酬,即:
FK = YK = θAσ-1σt (Yt Kt )1σ(5)
FL = YL = (1-θ)Bσ-1σt (Yt Lt )1σ(6)
早期的供给面系统估计是直接将(1)、(5)和(6)式进行估计,但是这种估计结果高度不稳定。为得到稳定的估计结果,本文对该系统进行标准化处理。假设对基准值有:
(1-θ)θ=w0L0r0K0 (7)
其中,带0下标的变量为基准值。易证A0=Y0/K0,B0=Y0/L0。将技术表示为At=A0exp[gK(t,t0)],Bt=B0exp[gL(t,t0)],其中,gi(t,t0)为要素效率的增长率(i=K,L)。
为进行标准化,引入一个规模因子ξ,使得Y0=ξY,K0=K,L0=L,t0=t。其中,Y、K、L、t分别是各变量的均值。并将要素效率的增长率设定为gK(t, t)=trKλK[(tt)λK-1],gL(t,t)=trLλL[(tt)λL-1]。其中,rK与rL为技术增长参数,λK与λL为技术曲率。值得注意的是,要素效率的增长率随时间变化而变化。当λK=1时,gK(t,t)=rK(t-t),这意味资本效率为常数增长率;同样,当λL=1时,gL(t,t)=rL(t-t),即劳动效率为常数增长率。因此,我们便得到具体的标准化的供给面方程组,如下所示:
ln(Yt/K)=ln(ξ)+σσ-1lnθKtKexp[gK(t,t)]σ-1σ+
(1-θ)LtLexp[gL(t,t)]σ-1σ
ln(rtKt/Yt)=ln(θ)+σ-1σln(ξ)+
1-σσln(Yt/KKt/K)+σ-1σ(gK(t,t)
ln(wtLt/Yt)=ln(1-θ)+σ-1σln(ξ)+
1-σσln(Yt/KLt/L)+σ-1σgL(t,t) (8)
三、实证模型设定和数据说明
由(1)式导出的模型可知,资本与就业的系数应一致,但现实情况并非如此。因此,为避免理论分析与实际情况的不一致,并为便于分析技术进步偏向对就业增长的影响,本文在计量模型设定中,剔除了资本投入对就业增长的影响。因此,根据(3)式和(4)式,将计量模式设定如下:
lnLit=c+c1lnDit+c2lnwitrit+εit(9)
其中,i为行业。由上式可知,技术进步的偏向和要素报酬率的比值直接决定了就业增长,通过计量分析,便可知技术进步偏向、要素报酬率比值与就业增长之间的关系。
本文选用1987—2013年中国的制造业数据,基于数据的可获得性,包括28个行业。鉴于制造业各行业的生产特征不同,参考蒙英华等(2010)对制造业28个行业的划分标准进行分类,劳动密集型行业包括14个行业具体包括食品加工、食品制造、饮料制造业、烟草加工、纺织业、服装及其他纤维制品制造、皮羽及其制造、木材加工及木竹藤棕草制品、家具制造、造纸及纸品业、印刷业和记录媒介的复制、文教体育用品制造、橡胶制品和塑料制品。 ,资本密集型行业包括8个行业具体包括:石油加工及炼焦、非金属矿物制品、黑色金属冶炼及压延加工、有色金属冶炼及压延加工、金属制品、通用设备制造、专用设备制造和仪器仪表制造。 ,技术密集型行业包括6个行业具体包括:化学原料及化学制品、医药制造、化学纤维制造、交通运输设备制造、电气机械机器材制造和通信设备及其他设备制造。 。其中,劳动密集型行业主要依靠大量劳动力投入,对技术和设备的依赖度较低;资本密集型行业拥有技术装备多、投资量大、劳动力较少,资本成本与劳动成本相比所占比重较大;技术密集型行业对技术和智力要素的依赖远远超过对其他生产要素的依赖。
研究技术进步偏向对中国制造业就业增长的影响,所需要的数据包括行业增加值、资本投入、劳动投入、资本报酬率和劳动报酬率。
行业增加值:1992年前《中国统计年鉴》只有净产值,而实际上,真正统计的行业增加值是净产值与提取的折旧基金之和,因此,利用此计算方法便得到1987—1992年的行业增加值。1992年后的行业增加值数据来自《中国制造业经济统计年鉴》和《中国统计年鉴》。同时,本文以1990年为基期,利用行业工业品出厂价格指数对行业增加值进行平减。
资本投入:将1987年年末行业固定资本形成作为初始资本存量,利用永续盘存法估算各行业年末的资本存量,其中折旧率取9.6%(张军,2004),并用行业固定资产投资价格指数进行平减。
劳动力投入:1987—2002年的行业年末职工人数数据来源于《中国制造业统计年鉴》,2003—2013年的行业年末就业人数数据来源于各年的《中国统计年鉴》,将相邻数据平均就可得平均职工数或平均就业人数,本文将其视为各年的劳动力投入。
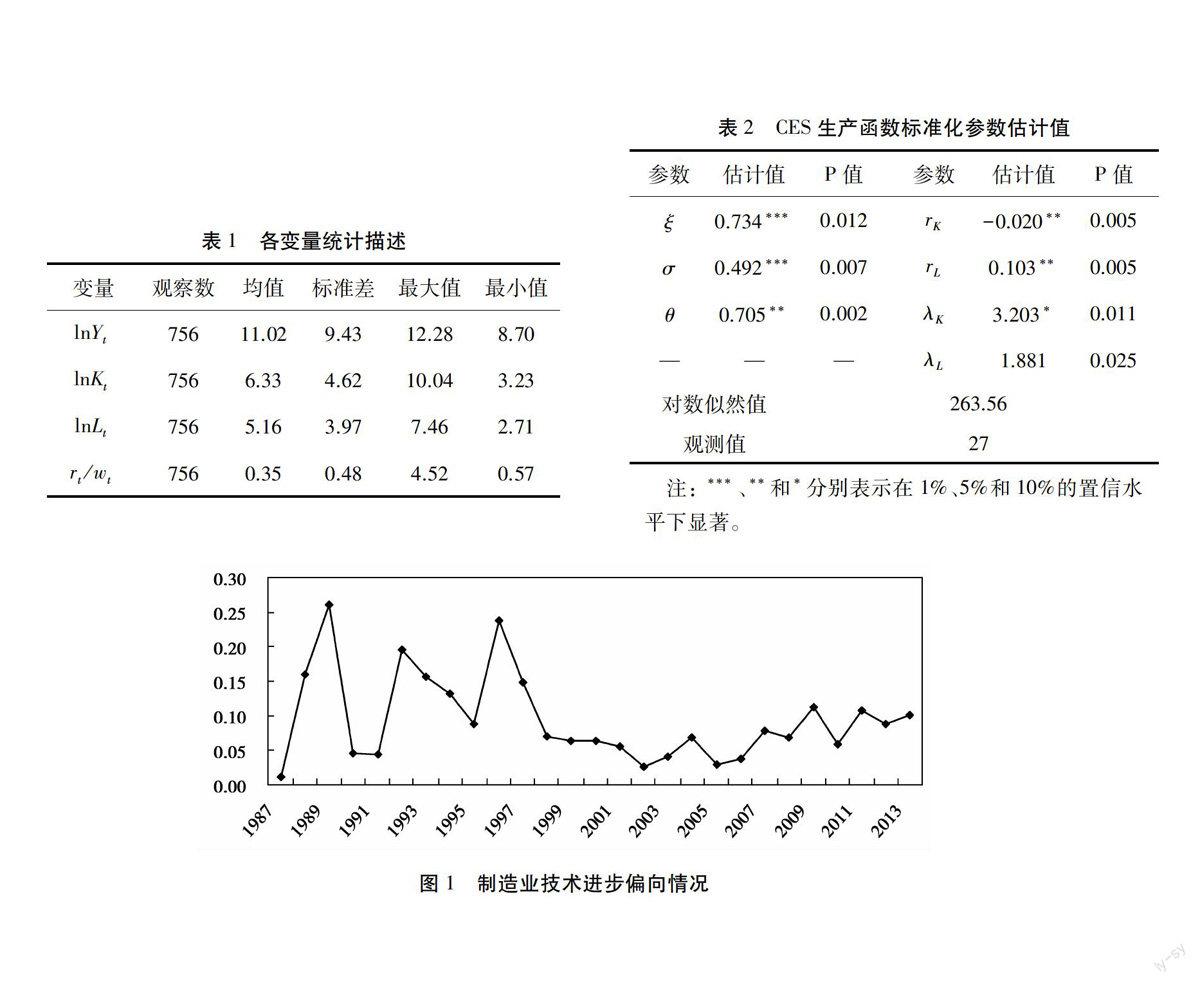
劳动报酬率和资本报酬率:《中国劳动统计年鉴》公布了历年城镇行业就业人员的平均报酬,将其视为行业劳动者报酬,并按1990年的消费价格指数进行平减。将历年行业劳动报酬乘以行业劳动力人数并除以行业增加值,便得到历年行业劳动者报酬率。在规模报酬不变时,资本报酬率=1-劳动报酬率。表1给出了各变量的统计描述。
表1各变量统计描述
变量观察数均值标准差最大值最小值
lnYt75611.029.4312.288.70
lnKt7566.334.6210.043.23
lnLt7565.163.977.462.71
rt/wt7560.350.484.520.57
四、实证分析
利用上述数据,根据方程组(8)估算要素替代弹性和要素分配参数,本文采用可行的广义非线性最小二乘法。由于该方法的估计结果可能对初始值敏感,因此,这里采用“全局最优”的方法。由于要素替代弹性是关键的初始值,本文尝试在(0,∞)寻找要素替代弹性的各种取值,找到使对数似然值最大的估计结果,也就是“全局最优”的估计结果,
估计结果如表2所示。表2中的要素替代弹性估算结果为0.492,略微高于整个工业的要素替代弹性值(0.481),表明在制造业部门生产过程中,资本与劳动之间是互补的。其中,劳动效率的增长参数rL为0.103,表明劳动效率的增长率为正;而资本效率的增长参数rL为-0.020,表明资本效率的增长率为负;要素之间的重要性分配参数θ为0.705。
表2CES生产函数标准化参数估计值
参数估计值P值参数估计值P值
ξ0.734***0.012rK-0.020**0.005
σ0.492***0.007rL0.103**0.005
θ0.705**0.002λK3.203*0.011
———λL1.8810.025
对数似然值263.56
观测值27
注: ***、**和*分别表示在1%、5%和10%的置信水平下显著。
将要素替代弹性值0.429代入(4)式,便可得到整个制造业行业的技术进步偏向情况,如图1所示。在1987—2013年,技术进步偏向值均在0线之上,这说明整个制造业技术进步偏向资本,其偏向均值为0.094。值得注意的是,在2000年前,制造业技术进步偏向波动较大;在2000年后,制造业技术进步偏向波动较为平缓。
图1制造业技术进步偏向情况
同时,将要素替代弹性值代入(5)式也可测算劳动密集型行业、资本密集型行业和技术密集型行业的技术进步偏向情况,如表3所示。在劳动密集型行业,除了1988年、1989年、1993年、1994年和2008年外,其他年份的技术进步均偏向资本,其均值为0.090;在资本密集型行业,1987年、1988年、1989年、1990年、1993年、1994年和2010年的技术进步偏向劳动,其他年份的技术进步偏向资本,其偏向均值为0.095;在技术密集型行业,除了1988年、1989年、1993年、1994年和2005年外,在其他年份技术进步均偏向资本,其偏向均值为0.128。值得注意的是,在三类行业中,技术密集型行业技术进步偏向资本的均值最大,这与现实行业的发展情况相吻合
我们首先利用(9)式分析整个制造业技术进步偏向对就业增长的影响,估计结果如表4所示。在固定效应模型和随机效应模型中,技术进步偏向在10%水平上负显著,这表明技术进步偏向每提高1个百分点,制造业的就业增长将下降0.113个百分点和0.128个百分点;劳动与资本的报酬比在1%水平上负显著,这表明劳动与资本的报酬比每提高1个百分点,制造业的就业增长将下降0.263个百分点和0.240个百分点。
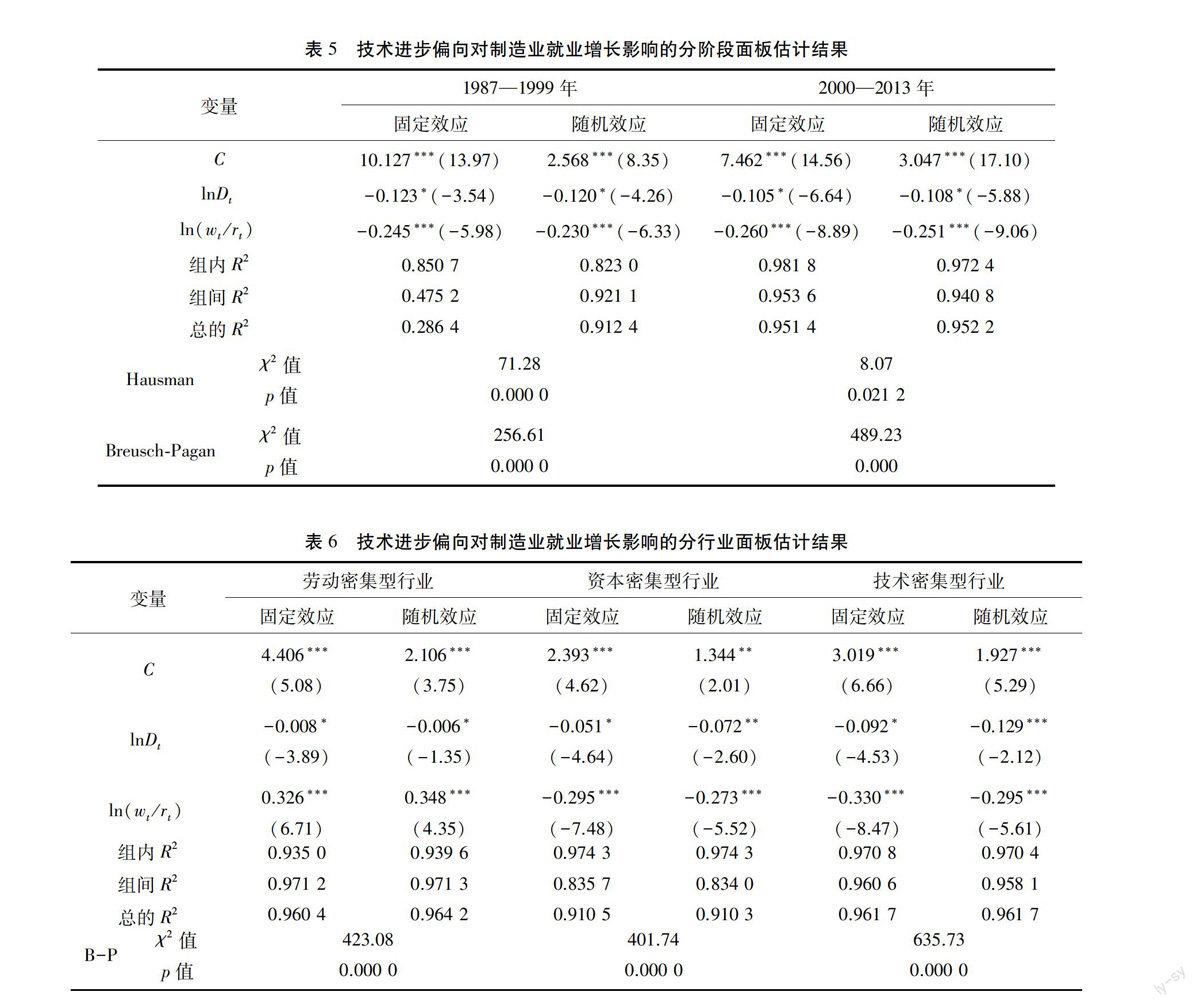
为进一步考察技术进步偏向对制造业就业增长的影响,本文根据图1中的技术进步偏向走势图,将样本划分为两个阶段:1987—1999年(第一阶段)和2000—2013年(第二阶段),并分别对其进行面板估计,估计结果如表5所示。与第一阶段相比,第二阶段技术进步偏向对就业增长的影响明显下降。以固定效应模型的估计结果为例,在第一阶段,技术进步偏向每提高1个百分点,就业增长将下降0.123个百分点,而在第二阶段,就业增长将下降0.105个百分点。这主要与2000—2013年间技术进步偏向的走势较为平稳有关。一些研究指出,改革开放以来,我国采用的是以资本积累为基础的粗放型增长方式,但是,近些年我国也注重人力资本的发展,减缓了技术进步偏向资本的速度,进而使得技术进步偏向对就业增长的抑制作用有所缓解。
在过去的二十多年里,制造业三种类型行业的技术进步基本偏向资本,是不利于扩大劳动力就业规模的,进而使技术进步对行业就业增长的影响表现为负效应,但是在不同类型行业这种影响的程度是不同的。本文分行业的估计结果如表6所示。技术密集型行业的技术进步偏向对就业增长的影响最大,在固定效应模型和随机效应模型中,技术进步偏向每提高1个百分点,就业增长将下降0.092个百分点和0.129个百分点;劳动密集型行业的技术进步偏向对就业增长的影响最小,在固定效应模型和随机效应模型中,技术进步偏向每提高1个百分点,就业增长将下降0.008个百分点和0.006个百分点;而资本密集型行业的技术进步偏向每提高1个百分点,就业增长将下降0.051个百分点和0.072个百分点。
根据表6,以随机效应模型的估计结果为例,我们具体分析在制造业行业中技术进步偏向、劳动与资本的报酬比对就业增长的影响:
从技术进步偏向角度看,劳动密集型行业在10%水平上负显著,而资本密集型行业和技术密集型行业在5%水平上负显著。若资本偏向型技术进步提高1个百分点,劳动密集型行业的就业增长将下降0.006个百分点,资本密集型行业的就业增长将下降0.072个百分点,技术密集型行业将下降0.129个百分点。这表明制造业大多数行业的技术路径均呈现出较强的资本替代劳动特征,因此技术进步对就业增长表现出抑制作用,即技术进步偏向资本在一定程度上加剧了“就业破坏”效应(王晓 等,2013)。值得注意的是,劳动密集型行业的技术进步偏向对其就业增长的抑制并不明显,主要原因在于劳动密集型行业的技术进步对劳动的替代相对较小。
从劳动与资本的报酬比角度看,劳动密集型行业在1%水平上正显著,而资本密集型行业和技术密集型行业在1%水平上负显著,这意味劳动与资本的报酬比提高1个百分点,劳动密集型行业的就业增长提高0.348个百分点,而资本密集型行业的就业增长下降0.273个百分点,技术密集型行业的就业增长下降0.295个百分点。这说明工资上涨是劳动密集型行业就业增长的主要因素;而在资本密集型行业和技术密集型行业中,工资上涨会使这些行业更多地使用价格相对低廉的资本,进而诱导行业的技术进步选择更加偏向资本。
五、结论与启示
本文基于要素增强型生产函数构建了技术进步偏向对就业增长影响的理论模型,并采用1987—2013年中国制造业数据进行了实证分析,结果显示:制造业部门中的资本与劳动之间的替代弹性大于0且显著小于1,表明资本与劳动之间呈现互补关系;1987—2013年,技术进步偏向值均大于0,说明整个制造业的技术进步明显偏向资本;同时,制造业三种类型行业的技术进步也基本是偏向资本的,其中技术密集型行业的技术进步偏向资本最为明显。进一步的实证分析表明:无论在固定效应模型还是在随机效应模型中,技术进步偏向对整个制造业就业增长具有抑制作用;但与1987—1999年相比,2000—2013年技术进步偏向对就业增长的影响明显下降;制造业大多数行业的技术进步具有较强的资本替代劳动特征,其中劳动密集型行业技术进步对劳动的替代较小;工资上涨是影响劳动密集型行业就业增长的主要因素,而工资上涨也会使资本密集型行业和技术密集型行业更倾向于使用价格相对低廉的资本,进而诱导其技术进步路径的资本替代劳动倾向更为明显。
目前,我国还是发展中国家,技术进步更多的是通过引进国外的先进机器设备或是采用国外先进的生产技术来实现的,而这样的技术进步路径选择需要大量资本品的投资和更高质量的生产要素的投入,容易造成对制造业部门劳动力的替代,尤其是导致劳动密集型行业中大量低技能劳动力的闲置。由此可以看出,制造业部门技术进步偏向与就业增长之间呈现非一致性关系,尤其是在经济新常态下,在经济发展速度放缓和经济结构转型的宏观经济环境下,技术进步与就业稳定增长的矛盾将会更为突出。因此,为保证制造业部门乃至整个中国的就业稳定增长,根据当前中国就业结构形势及人口老龄化趋势,在逐步提升各行业的技术水平的同时,还应注意合理引导技术进步的偏向。值得注意的是,如果过度关注就业稳定增长,很可能会牺牲前沿技术进步。而我国正处于由粗放型向集约型经济增长方式转变的过程中,意味着制造业部门必须通过技术创新实现创新驱动,进而实现经济增长方式的转变。那么,如何实现技术进步和就业增长的良性互动?解决这一矛盾的关键是:加强对前沿技术引进的宏观调控和管理,根据宏观经济环境和发展趋势合理化技术进步偏向;当前,应注意降低制造业资本替代劳动的速度,并大力发展中小企业,增强对劳动力的吸纳能力,提高劳动力的供需协调能力。
参考文献:
蒙英华,黄宁.2010.中美服务贸易与制造业效率——基于行业面板数据的考察[J].财贸经济(12):96103.
王林辉,董直庆.2011.技术进步和就业增长关联效应:基于MSVAR模型的动态分析[J].社会科学战线(1):6774.
王晓,崔友平.2013.技术进步与就业: 一个文献述评[J].云南财经大学学报(2):2126.
张军,吴桂英,张吉鹏.2004.中国省际物质资本存量估算:1952—2000[J].经济研究(10):3544.
钟世川.2014.技术进步偏向与中国工业行业全要素生产率增长[J].经济学家(7):4654.
朱翠华,李建民. 2012. 技术进步就业效应新解[J].财经科学(4):5361.
朱轶,熊思敏.2009.技术进步、产业结构变动对我国就业效应的经验研究[J].数量经济技术经济研究(5):107119.
ACEMOGLU D. 2010. When Does Labor Scarcity Encourage Innovation?[J]. Journal of Political Economy,118(6):10371078.
ACEMOGLU D. 2002. Directed technical change[J]. The Review of Economic Studies,69(4):781809.
ACEMOGLU D. 2003. Labor‐and capital‐augmenting technical change[J]. Journal of the European Economic Association,1(1):137.
AGHION P,HOWITT P. 1994. Growth and unemployment[J]. The Review of Economic Studies,61(3):477494.
ANTRAS P. 2004. Is the US aggregate production function CobbDouglas? New estimates of the elasticity of substitution[M]. Contributions in Macroeconomics, 4(1):11611162.
CYERT R M,MOWERY D C. 1987. Technology and employment:Innovation and growth in the US economy[M]. National Academies Press.
KLUMP R,MCADAM P,WILLMAN A. 2007. Factor substitution and factoraugmenting technical progress in the United States:a normalized supplyside system approach[J]. The Review of Economics and Statistics,89(1):183192.
ZULETA H. 2008. Factor saving innovations and factor income shares[J]. Review of Economic Dynamics,11(4):836851.

