柔性钢支撑结构的一种计算
■秦 伟 ■中铁二十三局集团第一工程有限公司,山东 日照 276826
目前,在基础工程施工中,例如在施工陆地基坑时,支护广泛采用钢支撑,水中基坑采用钢板桩等进行支护,这些结构适用于因受场地等条件的限制,基坑或基槽不能采用放坡开挖、周围有水或淤泥而必需进行垂直土方开挖施工时采用。
1 支护结构计算方法的比较
在设计支护结构时,结构承受的土压力与土层地质条件、地下水状况、支护结构各构件的刚度以及施工工况、方法、质量等因素密切相关,且呈现出时空效应,由于这些因素千变万化,十分复杂,因此难于计算土压力的精确值,目前国内外常用的计算土压力方法仍以库仑公式或朗肯公式为基本计算公式。库仑公式及朗肯公式均为假设土体为极限平衡状态下的计算公式,支护结构计算方法主要为等值梁法。古典的静力平衡法、等值梁法均不考虑支撑变形,将土压力作为外力施加于支护结构,然后通过求解水平方向合力及支撑点弯矩为零的方程得到结构内力。但实测资料表明,围护结构并不是刚性的,其变形和土压力的调整使得作用于基坑围护结构上的土压力往往处于非极限平衡状态,与按经典方法计算的结果相差较大,存在较大的安全隐患。虽然这些方法未考虑墙体变形及墙体与土的相互作用,但在工程界仍广泛运用。

图1.1 弹性地基梁法计算模型
基坑开挖是一个土与结构共同作用的复杂过程。对土介质本构关系的模拟是采用土与结构共同作用方法的关键。基坑现场的土体应采用合适的本构模型进行模拟,并且能根据室内实验和原位测试等手段给出合理的参数。
根据目前土力学理论的研究情况,在所有理论模型中,修正剑桥模型、Plaxis Hardening Soil(HS)模型均是硬化类型的本构模型,能同时反映土体在小应变时的非线性行为和土的塑性性质,更适合于基坑开挖的分析。这种观点将土体比作连续弹性支承,不考虑被动土压力,只考虑主动土压力,其受力过程中,应变及应力按照非弹性线形变化,在这种理论发展起来的计算方法主要是弹性地基梁法,这种计算模型(见图1.1)是将支护结构分成若干段,用弹簧结构模拟土体的被动压力,计算时采用有限元方法,能够比较细致得出各个节点的受力和变形情况。
2 计算实例
2.1 地质概况
东明黄河大桥黄河水中共有7 个墩,围堰范围主要土质为粉砂,粉质黏土,粉土,土层厚度及分布范围基本一致。以K56 +978.66 处B9勘探孔地质资料为例,土层分布及土层性质见下表2.1:

表2.1 地质土层参数表
2.2 水文概括
4 月份测定河水流速2m/s;水深按最大5m 考虑,冲刷深度在水位深处按照2m 考虑。
2.3 围堰构造
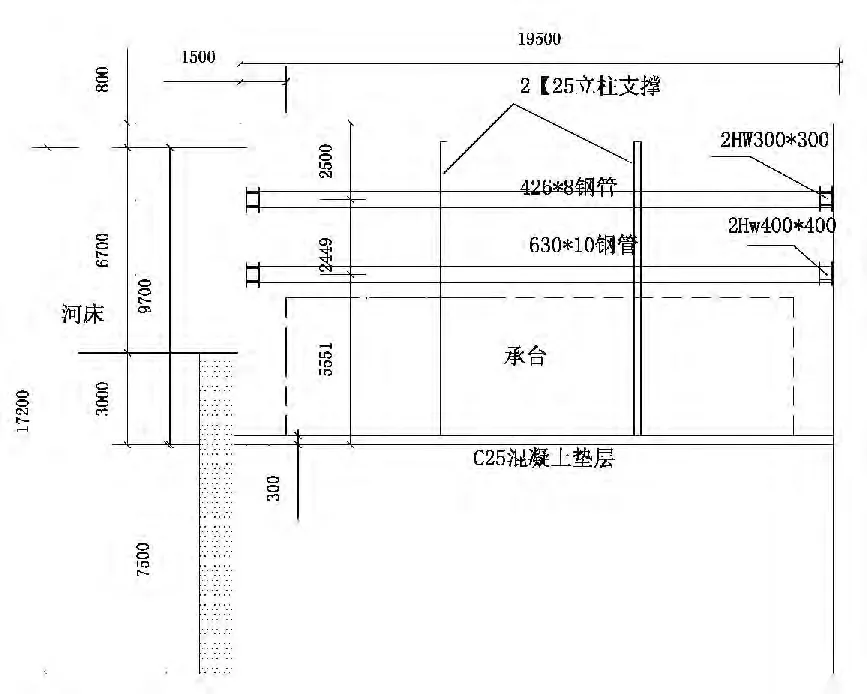
图2.1 钢板桩围堰断面图
钢围堰材料采用拉森Ⅳ钢板桩,钢板长度18 米,顶标高62.30m,钢板桩相互咬合连接成封闭式结构,见图2.1。围堰尺寸为26.6 ×19.6m 见图2.2,围堰内部设置整体式围檁,分上下两道,最下层围檁放置在承台顶0.5m 处。上下围檁横撑要联接,增加稳定性,围檁分3 阶段施工,第一阶段为下放期,安装主框架,第二阶段抽水至上围檁以下,安装支撑构件,第三阶段挖土抽水至下围檁下,安装下支撑,形成整体结构,最后段进行清底封底作业。

图2.2 支撑结构图
2.4 计算参数
粉砂层土体性质为:密度γ1=19KN/m3,内摩擦角φ1=26°,粘聚力c1=10kpa;粉砂浮容重:γ1w=19-10=9KN/m3
粉质黏土密度γ2=18KN/m3,内摩擦角φ2=20°,粘聚力c2=10.5kpa;粉质黏土浮容重:γ2w=18-10=8KN/m3
粉砂层主动土压力系数:
Ka1=tg2(45°-)=0.39,=0.625
被动土压力系数:
Kp1=tg2(45° +)=2.56,=1.6。
2.5 抽水至混凝土垫层底时钢板桩受力计算
采用弹性地基梁模型,钢板桩材料梁单元模拟,划分为多段,分别设弹性支撑,围檁的支撑点及土体均采用土弹簧模拟。
上围檁钢支撑的弹簧刚度为K=412714kN/m;
下围檁钢支撑的弹簧刚度为:K=
αR—为支撑松弛系数,取0.9;
λ-支撑不动点调整系数,取0.5;
E—支撑的弹性模量,取2.1 ×109kpa;
A—支撑的截面积,取a=0.63 ×3.14 ×0.008=0.0158m2
Lo--支撑长度,取19.6m;
s--支撑间距,取5m;
ba--计算宽度,取1m。
根据以上参数,计算得K=610416KN/m。
在开挖面至以下4m 的土体的弹簧刚度计算采用公式:
KH=bhmz
h—为支点处上下分段的平均长度;
m—为地基水平抗力系数的比例系数,根据建筑基坑规范,依地层土性状取值为m=4000~6000KN/m4
z—为支点上下两段土层距离地面的深度;
b—为计算宽度,取1m。
以下部位的土体弹簧刚度按照下列公式计算:
KH=kHbh
KH——水平向基床系数,按照稍密砂土取15000~30000KN/m3。
土弹簧的刚度系数计算结果如下表2.1:

表2.1 地基土刚度系数计算表
采用Midas/Civil 的计算模型及荷载见图2.3:
计算结果为:
根据反力图(见图2.4),上围檁所承担反力为F1=-42KN/m,下围檁所承担的反力为F2=308.3KN/m。
根据内力图(见图2.5),钢板桩最大弯矩为M=-245.7KNm。
每米钢板桩最大应力为
f=M/0.9W
=120.26MPa <[f]=270MPa。
与应力(见图2.6)计算结果126.9MPa 基本一致。
根据变形图,钢板桩最大位移发生在中部,而钢板桩底部位移非常小。
3 施工监控分析

图2.3 钢板桩计算模型及荷载

图2.4 反力图
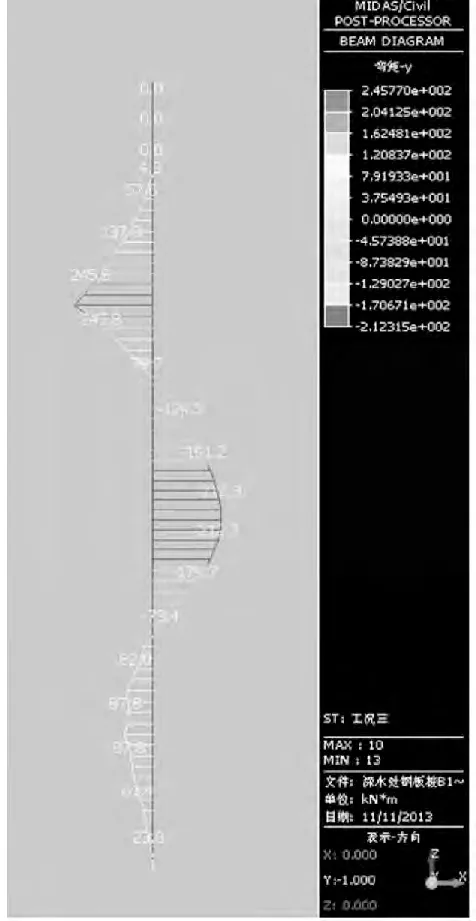
图2.5 内力图

图2.6 应力图
在钢围堰施工过程中,我们对钢板桩的受力和变形情况进行了监控,在承台以上分3 层布置应变计和压力盒。对钢板桩进行了顶压试验。钢板桩的应力值见表3.1.

表3.1 钢板桩应力监测表
根据监控表,可以看出,实际监控数据与计算数值基本一致,略小于计算值。
4 结论

图2.7 变形图
柔性钢支撑的受力计算与刚性支撑(如挡墙)的计算有所差别,不能都采用经典土力学计算,所以采用弹性地基梁可以更好的模拟土体本构关系,计算成果更接近实际,而且这种计算配合有限元软件比较简便直接,在工程施工中比较容易做到,是一种值得推广的一种计算方法。
——结构相互作用的影响分析

