煤矿清洁生产模糊层次综合评价模型及应用

焦瑞峰，皇甫卓然，王 磊

（黄河水资源保护科学研究院，郑州 450004）

煤矿清洁生产模糊层次综合评价模型及应用

焦瑞峰，皇甫卓然，王 磊

（黄河水资源保护科学研究院，郑州 450004）

基于煤矿清洁生产评价的特点、目的，阐述了建立煤矿清洁生产综合评价指标体系的原则、内容、结构及评价的基本思路。将模糊数学和层次分析法相结合，建立了一种煤矿清洁生产综合评价决策模型，论述了其的方法和原理，并且用实例验证了模型的实用性、有效性。从而丰富了煤矿清洁生产评价的方法。

煤矿清洁生产；指标体系；模糊集合；层次分析法；评价方法

引言

清洁生产是指不断采取改进设计、使用清洁的能源和原料、采用先进的工艺技术与设备、改善管理、综合利用等措施，从源头削减污染，提高资源利用效率，减少或者避免生产、服务和产品使用过程中污染物的产生和排放，以减轻或者消除对人类健康和环境的危害[1]。2008年11月，环境保护部颁布《清洁生产标准 煤炭采选业》（HJ446-2008），2009年2月1日开始实施。标准中规定了煤炭采选业清洁生产的一般要求，列出了7项清洁生产标准指标。

目前，煤炭企业清洁生产评价并没有给出确切的核定评价结果的方法，在煤炭采选业建设项目的环境影响评价进行清洁生产评价中，一般都是采用单指标评价法[2]，即对照《清洁生产标准 煤炭采选业》（HJ446-2008）的标准进行对比，如果某一指标低于某一级别的标准，其清洁生产水平即降一级。该方法的优点是直观、简便，缺点是不能反映煤矿整体清洁生产水平情况。本文将模糊数学和层次分析方法相结合，建立了能同时考虑不同生产情况对清洁生产状况影响的模型。

1 建立煤矿清洁生产综合评价的指标体系

1.1 煤矿清洁生产综合评价的基本思路

煤矿清洁生产综合评价的方法要解决两个主要问题：1）两类不同指标的单指标评价方法；2）多指标评价结果综合方法。无论是单指标还是综合评价结果，都是一个不确定性的概念，具有模糊性。以综合评价方法的要求和指标体系的特点，设计模糊层次综合评价方法的基本思路为：用层次分析法确定各指标的权重，在此基础上用模糊综合评判理论进行单指标评价和综合评价。

1.2 煤矿清洁生产评价指标体系的建立

进行煤矿清洁生产综合评价首先要设立相应的综合评价指标体系。一般应遵循以下几项原则：1）完全性原则，建立的指标体系应能全面反映煤矿生产的各方面特性；2）简单性原则，指标体系既要全面但又不是愈多愈好，而应抓住主要方面又使分析计算及相应工作量简捷；3）客观性原则，指标的选取应坚持事实求是、尊重客观，力争避免主观倾向性。

根据上述原则，以及《清洁生产标准 煤炭采选业》（HJ446-2008）的标准，建立能全面反映煤矿清洁生产状况的清洁生产综合评价指标体系，可归纳为如表1所列

的各项内容。在评价中应依据评价的目的、煤矿的类型及需要考核的内容、环境特点及煤矿的特征，选用不同参数评价煤矿的清洁生产水平。

表1 煤矿清洁生产综合评价指标体系

2 模糊层次综合评价的方法原理

模糊评价（评审、评判、决策），即在评价过程中引入模糊性概念，运用模糊数学来处理煤矿清洁生产评价的一些问题，以反映煤矿清洁生产状况。例如某煤矿清洁生产评价结果一般用国际先进水平、国内先进水平、国内基本水平等来表示，而所谓国际、国内先进水平和国内基本水平等划分，具有模糊性。模糊数学是研究对这些模糊性问题进行定量处理的一种方法；层次分析法（AHP）是用于进行定性和定量因素相结合的一种有效决策方法。将这两种方法互相结合对煤矿清洁生产进行综合评价的方法称为模糊层次综合评价。

模糊层次综合评价中涉及的基本要素和主要方法可简要归纳如下。

2.1 建立评价因素（指标）集

U={u1，u2，…，uj，…，un}，指煤矿清洁生产综合评价指标的集合。

2.2 建立（决策）评语集

V ={V1，V2…，Vi…Vm}，表示评价分级（例：国际先进水平、国内先进水平、国内基本水平和未到达清洁生产或Ⅰ级、Ⅱ级、Ⅲ级、Ⅳ级等四个等级）评语的集合。

2.3 建立隶属函数确定单因素评判矩阵R

应用模糊数学的基本概念，评价因素集中每一个指标隶属于评语集中不同评语分级（是一个模糊集合）的程度，称为隶属度[3]。隶属函数和隶属度是模糊数学中最基本的概念。前者一般以μV（x）表之，其含义是：因素集U中某一指标x（相当于指标U ）隶属于模糊集合V（相当于评语集V，这是模糊集合）的程度，其取值在[0，1]区间，并以rji表之。此值即为指标uj的隶属度。隶属函数的形式，可视评价指标的特征确定或选用已有的公式，评价因素集U中全部指标隶属度的合成，即为单因素评价矩阵。

参考煤炭采选业清洁生产标准，若某指标的取值范围为[a，b]。根据人们对其判断和敏感性程度，将[a，b]分为与评语集Vi（i =1，2，3，4）相对应4个区间[a1，b1]、[a2，b2] 、[a3，b3] 及 [a4，b4]。若将Vi看成是[ai，bi]上的普通集合，则会造成两个区间的边缘点数值相差不大，而评语却相差一个级别的不合理现象。为了消除这种不合理现象，需进行模糊化处理。在清洁生产评价中可取各级清洁生产标准值对应的隶属度，取最大值1.0，而相邻两区间互相交叉。这样，对某个指标的具体数值，可以以不同的隶属度，分归于不同的模糊集合Vi和Vi+1（i =1，2，3，4）。

根据各指标的特征，拟定各隶属函数为线性函数，并且满足：若μvi（uj）=1.0，则μvi+1（uj）=μvi-1（uj）=0，如图1所示。其数学表达式为：

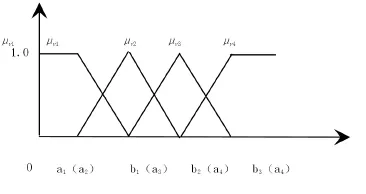
图1 Vi（i=1，2，3，4）的线性隶属函数

此处，μvi（uj）表示指标uj隶属于评语集Vi的程度，亦即隶属度rji在[0，1]区间的取值，如图2所示。但端点的μv1（uj）及μv5（uj）其函数及图形略有不同（见图1，详见实例）。

图2 隶属度rji在[0，1]区间的取值

利用上述方法，具体拟定（或选定）煤矿清洁生产指标uj相应的隶属函数，将各指标值代入相应的隶属函数，即可求得各指标的单因素的不同隶属度rji，并得单因素评判结果为Rj=（rj1，rj2，rj3，rj4，rj5），j =1,2,…,n，综合各指标的评价结果得单因素评价矩阵如下

2.4 用层次分析法确定各因素（指标）的权重W=（W1,W2，…，Wn）

通过上述步骤，已经确定了各单因素的评判结果和单因素评判矩阵R，但各因素相对于煤矿清洁生产评价目标，其各自的影响权重数尚不得而知。模型中采用层次分析法确定权重。其具体步骤如下。

2.4.1 两两比较构造判断矩阵

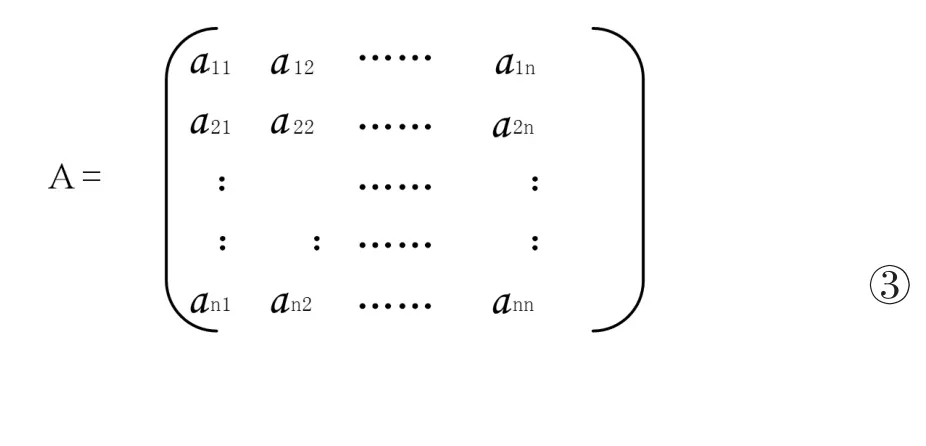
根据上文建立的煤矿清洁生产综合评价指标体系，通过两两比较，构造判断矩阵A，即：

aij表示相对于煤矿清洁生产状况而言指标ui与uj的比较，采用1～9的标度得到的ui比uj重要的程度[4]。

2.4.2 计算重要性排序

求判断矩阵A的最大特征根所对应的特征向量W =（W1，W2，…，Wn）即为所求的各指标的权重。

2.4.3 一致性检验

计算判断矩阵A的最大特征根λmax

其中，（AW）i表示向量AW的第i个元素。则判断矩阵的一致性检验指标CR为

当CR≤0.1时，一般认为判断矩阵具有满意一致性，说明确定的各指标的权重是合理的，否则需对判断矩阵进行调整，直至具有满意的一致性。

2.4.4 模糊层次综合评价

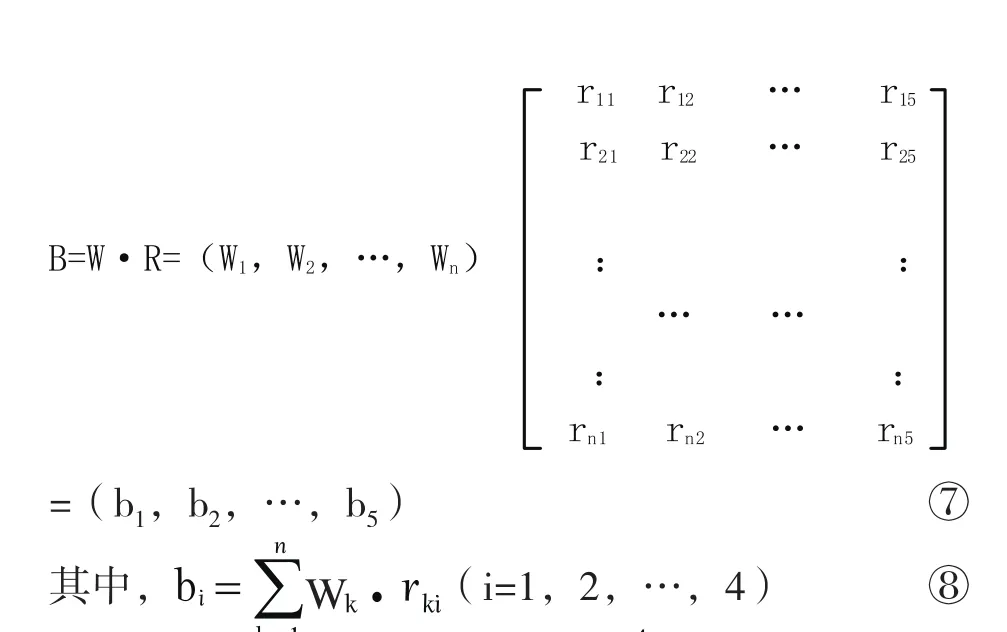
3 煤矿清洁生产模糊层次综合评价实例

3.1 基本数据及评价指标

某煤矿生产情况数据见表2。

表2 某煤矿生产情况数据统计表

3.2 评价指标及标准

根据煤矿生产情况确定评价指标集U={u1，u2，u3}

根据清洁生产标准（HJ446-2008）可得以上七类指标清洁生产标准（见表3）。

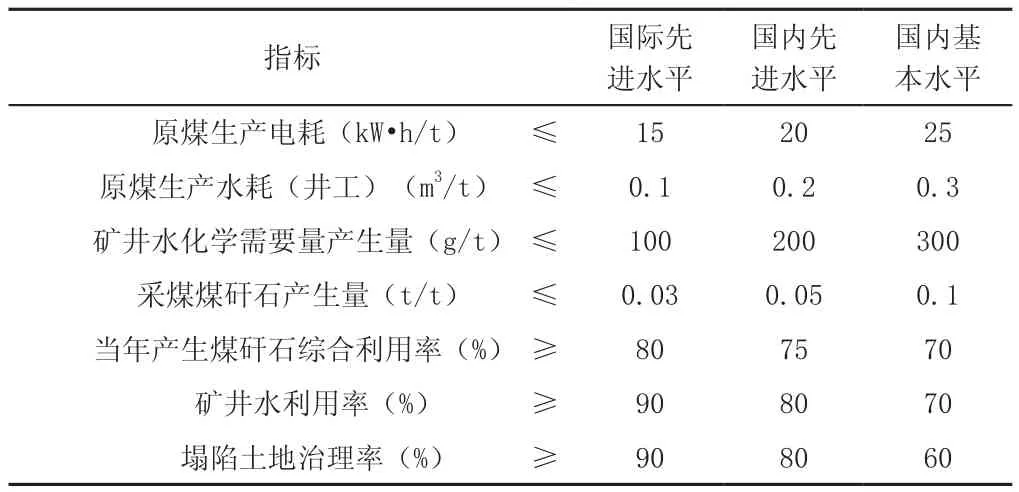
表3 生产情况相应的清洁生产标准（HJ446-2008）

3.3 根据各指标的特征，拟定各指标相应的隶属函数

（如图3所示）

3.4 建立单因素评价矩阵

按式①和图3具体选定生产指标μj相应的隶属函数，将各指标值代入得单因素评价矩阵R。

原煤生产电耗：

井工原煤生产水耗：

矿井水化学需氧量产生量：

图3 各参数的隶属函数

采煤煤矸石产生量：

当年产生煤矸石综合利用率：

矿井水利用率：

塌陷土地治理率：

综上得单因素评价矩阵 ，即

3.5 确定各因素的权重W＝（W1,W2,W3,W4,W5）

（1）通过专家对该例指标体系中的指标两两比较得判断矩阵A为

（2）由式④计算判断矩阵A的最大特征根所对应的特征向量

W=（W1,W2,W3,W4,W5,W6,W7）=（0.261,0.246,0.1340, 150,0.071,0.067,0.071）为各指标的权重。

（3）进行一致性检验

根据式⑤和式⑥计算：

所以判断矩阵A具有满意一致性，可用作综合评价模型各指标的权重。

（4）清洁生产综合评价结果由式⑦得综合评价结果为：

据此判断，该煤矿清洁生产水平为Ⅱ级，即：国内清洁生产先进水平。

4 结论

煤矿的清洁生产水平综合评价，问题复杂，涉及因素众多，本文将模糊数学和层次分析法相结合建立了模型，考虑了煤矿的清洁生产水平评价结果的模糊性，用层次分析法确定权重在一定程度上克服了专家直接给定法的主观任意性，并且可同时考虑不同方面的生产情况对清洁生产的整体影响。实例运用证明模糊层次综合评价的模型是客观、合理、可行的。

[1]中华人民共和国环保部.清洁生产标准 煤炭采选业[Z].2009.

[2]陆雍森.环境评价（第二版）[M].上海：同济大学出版社，1999.

[3]闫家杰，赵万忠，迟凤起.模糊数学基础及应用初级[M].郑州：河南教育出版社，1993.

[4]赵焕臣，许树柏，和金生.层次分析法[M].北京：科学出版社，1986.

Comprehensive Assessment Model of Fuzzy Administrative Levels of Cleaner Production in Coal-mine and Its Application

JIAO rui-feng, HUNGFU Zhuo-ran, WANG lei
(Yellow River Protection Institute of Water Resources, Zhenzhou 450004, China)

Based on the characteristics and intent of cleaner production assessment in coal-mine, the paper expatiates to establish the principle, content, structure and the assessment basic consideration of index system of the cleaner production comprehensive assessment in coal-mine. The paper integrates the fuzzy mathematics with the analyzing method of administrative levels, establishes a comprehensive assessment decision-making model of cleaner production, discusses its methods and principle, and uses the examples to validate the practicability and effectiveness of the model.

cleaner production in coal-mine; index system; fuzzy integration; analyzing method of administrative levels; assessment method

X382

A

1006-5377（2015）10-0033-05

注：本文为水利部公益性行业科研专项（201101006）。