光伏发电量的预测综述
张 玉,张振涛,莫 寒
ZHANG Yu, ZHANG Zhen-tao, MO Han
(桂林理工大学 广西建筑新能源与节能重点实验室,桂林 541004)
0 引言
面对全球日益严重的能源危机,人类加快了对新能源探索的脚步。太阳能作为目前全球最大的可再生能源,具有极高的利用价值。发电量预测是太阳能利用的一项非常重要的指标,对大电网的分配调度会产生一定的影响。然而光伏阵列的输出特性受到光照强度、温度、湿度等其他外界因素的影响,具有不确定性[1,2],这使得光伏发电量的预测变得更加困难。
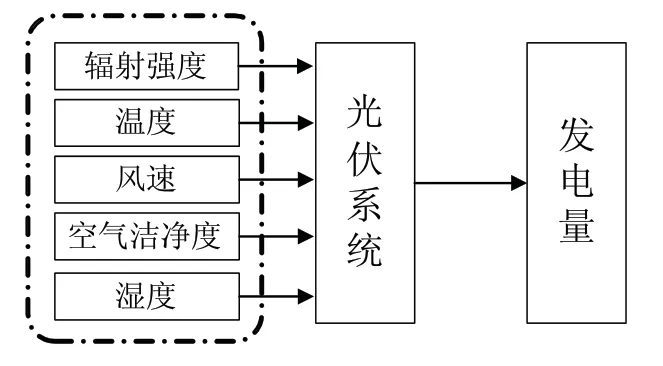
图1 光伏发电量受环境因素影响示意图
对于一个光伏发电系统,其发电量的预测对于大电网调度十分重要,我们需要掌握的是该系统在某一时刻的实时发电功率,在不同情况下选择合理的预测方法对发电量预测能起到事半功倍的效果。目前光伏发电量的预测方法有很多种,按照时间尺度可以分为超短期预测、短期预测和中长期预测。按照研究过程可以分为直接预测和间接预测[3]。这些方法虽然可以将大多数的预测方法进行归类,却很难全面覆盖,甚至有些预测方法的划分界限十分模糊,不能系统的将光伏发电量预测的方法进行归类。为此本文将光伏发电预测方法用数学统计预测法和人工智能预测进行分类,并在最后补充了一些其他的预测方法。实现了光伏发电量预测的完整化分类。
1 数学统计预测法
1.1 灰色理论预测法
所谓灰色理论预测法就是指利用灰色系统实现的预测模型。灰色系统的概念是在1982年由邓聚龙教授首次提突出,他所描述的是介于部分信息已知的白色系统和部分信息未知的黑箱系统之间的过度系统。灰色系统可以通过对原始数的分析整理找出它们之间存在的联系从而预测数据的变化规律从而达到预测的效果。GM(1,1)模型是灰色系统中较为常用的动态预测模型,该模型的构成只有一个单一变量的一阶微分方程,预测过程大致可以分为累加—拟合—累减三个步骤[4]。
文献[5,6]分别采用GM(1,1)模型对光伏发电量进行预测,单一的采用GM(1,1)模型对光伏的发电量虽然可以起到预测的效果,但其预测结果与实际结果存在一定的偏差,为了能够得到较为准确的预测结果,采用GM(1,1)残差修正模型对原有的预测模型进行修正。将一天中各个时间段的发电量构成一个时间序列,以一天中光照强度最强发电量最大时为分界点,把一天中的预测分为两个阶段分别进行预测。结果显示,基于残差修正的GM(1,1)模型效果更好,其预测结果更为接近实际值。
1.2 多元线性回归预测法
在生活中一种现象的发生往往与多个因素存在相互关联,此时就需要多个相关因素作为自变量解释因变量的变化规律,这种模型就是多元线性回归模型。在光伏发电量预测中,光伏系统的发电量受到辐射强度和温度等因素的影响,因此可以以这些因素作为光伏发电系统的多元线性回归模型的输入。
文献[7]将由18块京瓷KC130GH-2P多晶硅太阳能电池组件串联的光伏阵列作为研究对象,对该系统的辐射强度、环境温度、组件背板温度、风速、发电功率以及每小时发电量6个自变量建立多元线性回归模型,并采用F检测法对回归方程显著性检测后说明该模型有很好的拟合效果。将对预测结果在不同的天气情况下进行分类,在晴天,多云,阴转天三种情况下与将预测值与实际值比较后发现,在晴天的预测值较实际值偏高,阴转云的情况下预测值较实际值偏低,多云天气的预测值则有较好的预测效果。
1.3 时间序列预测法
时间序列预测法是一种以时间为序列,根据历史数据揭示事物发展规律的数学统计方法。在光伏发电量预测技术中将光伏系统某一时段内的发电量看作一个随时间周期变化的随机数列。通过曲线拟合和参数评估来建立预测系统的数学模型,自回归—滑动平均模型(ARMA)是时间序列预测法中较为常见的预测模型。文献[8]中作者建立了ARMA模型在光照充分的晴天下对光伏系统的短期发电量进行预测,结果表明,ARMA模型在晴天中有较高的预测精度。
数学统计预测法虽然在光伏发电量预测中可以实现预测的效果,其预测结果虽然和历史数据存在着某种相互联系,但这种联系并不能起到决定性的作用。在短期预测中光伏发电量受环境因素影响时效性较强,这种特性导致此类方法一旦受到环境因素变化较大情况时,预测结果变化缓慢,预测精度较低等情况。但这种方法易于实现,正是由于与历史数据存在着相互联系使得在中长期发电量变化趋势上有一定的可取性。
2 人工智能预测法
2.1 BP神经网络预测法
BP神经网络是一种按照误差逆向传播算法训练的多层前馈网络,是由大量的神经元相互连接而成的非线性动态系统,使用最速下降法通过反馈结果进而不断调整网络的权值和闸值,使网络的输出达到最优化。BP神经网络模型包括输入层,隐含层和输出层三个部分。目前,通过BP神经网络与其他算法相结合可延伸出多种预测方法,如基于牛顿法小波神经网络预测模型,基于遗传算法神经网络预测模型,基于BP神经网络—马尔科夫链预测模型,基于粒子群BP神经网络预测模型等。
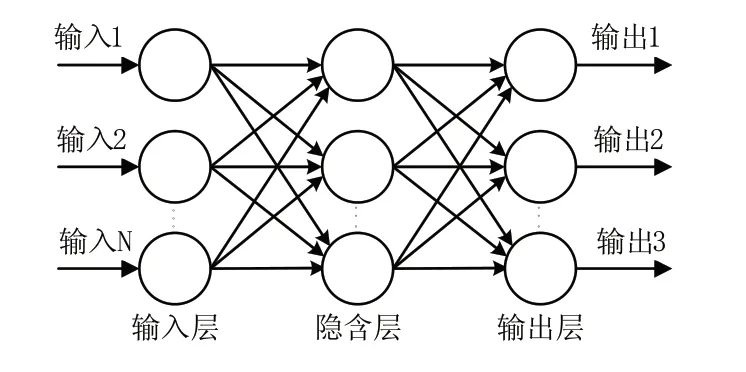
图2 BP神经网络结构示意图
2.1.1 基于牛顿法小波神经网络预测模型
文献[9]描述了一种基于牛顿法小波神经网络的光伏发电预测模型,在原有神经网络的预测模型中做了以下两点改进,其一在训练方法上选择能够较好地处理复杂问题的拟牛顿算法;其二是在神经网络的结构上采用能够较好处理小信号的小波神经网络进行改进。通过仿真结果分析发现,该模型比普通的神经网络预测模型预测精度更高,尤其针对不同季节采用该模型有较好的预测效果。
2.1.2 基于遗传算法神经网络预测模型
文献[10]描述了一种改进的神经网络算法,在神经网络的基础上加入遗传算法,建立GA-BP预测模型。首先对环境温度、风速、湿度、辐射强度等环境因素进行主成分分析,剔除掉无用信息并筛选出主要成分作为GA-BP预测模型的输入。设定初始种群数,经过遗传迭代,得到BP神经网络的最优权值和闸值,经过BP神经网络训练后得到最终预测结果。对预测结果分析后表明主成分分析的遗传优化神经网络预测模型比一般的BP神经网络预测模型在预测结果上更为准确。
2.1.3 基于BP神经网络—马尔科夫链预测模型
文献[11]中提到一种基于BP神经网络—马尔科夫链的光伏发电预测方法,将前一日的发电量及最高和最低温度以及预测日当天的最低和最高温度作为模型的输入,在经过BP神经网络预测后根据预测的相对误差采用马尔科夫链模型进行修正。避免了在建模的过程中忽略了实际的光照数据等。结果表明该模型具有较高的预测精度。
2.1.4 基于粒子群BP神经网络预测模型
文献[12]中描述了一种基于粒子群的BP神经网络(PSO-BP)光伏发电预测模型,该模型将神经网络中需要调整的权值和闸值映射为PSO中的粒子,通过粒子间的竞争与合作不断优化这些参数,使网络的训练效率大大提高。通过与普通BP神经网络的预测结果相比较,基于PSO-BP神经网络的光伏发电预测模型有更好的预测效果。
2.2 支持向量机预测法
支持向量机(SVM)是1995年由Corinna Cortes和Vapnik提出的,是一种基于统计学习理论的模式识别方法,在解决一些复杂的非线性系统中具有极好的效果。其主要思想可以概括为将一个样本空间映射到一个高维空间中,在原有样本空间中线性不可分的问题在高维空间中实现线性可分。
2.2.1 基于鲁棒学习最小二乘支持向量机预测模型
文献[13]中提到了一种改进后的基于鲁棒学习最小二乘支持向量机(RLS-SVM)的光伏预测模型。在传统的LS-SVM基础上采用鲁棒学习提高系统的鲁棒性,同时减少了系统的“过拟合”现象。该模型以历史发电量,太阳辐射强度和环境温度作为输入,以光伏发电功率为输出,与LS-SVM模型及RBF神经网络做了仿真对比。研究结果表明,RLS-SVM光伏预测模型有更高的预测精度,能够准确的预测出光伏阵列额定输出功率,有效地解决了光伏发电的随机化问题。
2.2.2 基于相似日和最小二乘支持向量机预测模型
文献[14]提出了一种基于相似日和最小二乘支持向量机的光伏发电预测模型,该模型首先将天气因素归类为晴天、阴天和雨天。将温度和湿度作为两个主要参考量,计算出预测当日与历史数据的相似度,根据相似度选择相应的相似日,由相似日的光伏发电量和预测日当天的气候特征来预测这一天的发电量。这种模型在一定程度上减小了天气变化对预测值的影响,相比于SVM模型有更好的预测效果。
人工智能预测法有预测精度高、响应速度快等优点,BP神经网络和支持向量机预测法是目前较为常用的人工智能预测法,许多其他的智能预测模型也都是基于这两者加入其他算法进行改进。而这也使原本复杂的系统实现起来更为困难,尤其BP神经网络需要大量的原始数据进行训练。而支持向量机面对大规模的训练样本时更是难以实施。这些预测方法理论性较强,只能借助计算机实现仿真分析,很难与大型光伏发电站的实际情况相结合。
3 其他预测方法
在研究光伏阵列的数学模型中,我们不难发现影响光伏发电量的主要因素是温度和辐射强度[1,3]。针对这一特性,人们提出另外一种间接预测光伏发电量的方法,即建立瞬时太阳辐射模型,例如Hottel辐射预测模型或者Liu-Jordan辐射模型[15]等。这种预测方法以天文辐射作为输入变量,以地表接收到的太阳辐射为输出建立数学模型来间接预测实时的光伏发电量。同样利用此方法建立逐时太阳能预测模型和日总太阳能预测模型,可以实现以日为单位的光伏发电量。但这种方法实施起来十分困难,目前国内外对这方面的研究尚处在起步阶段。
从光伏电池板的电路特性出发可以直接采用日本工业标准(JIS)进行光伏发电量的预测,这种方法较为简单,通过光伏阵列的I/V特性曲线由数学公式计算出其输出功率。与之相似的三维模拟计算法则是寻找输出的瞬时最大功率,计算出瞬间的发电量并将其累加起来进而算出一天的发电量乃至一月的发电量。该方法充分考虑了影响光伏发电量的各个因素,包括太阳高度角的选择及配线方案等[16]。但这些方法仅在理论上存在可行性,实际实施起来具有一定的困难。
4 我国光伏发电量预测的发展现状
目前我国正在走可持续发展的道路并且大力推进“生态文明”建设,对能源的要求向着清洁环保的方向发展。在这样的时代背景下我国的光伏发电产业得到了迅猛的发展。
根据德国商报报道,2014年最新全球十大光伏供应商排名中中国企业就有四个之多,常州天合光能有限公司更是首次成为全球最大的光伏供应商。其他三家分别为中国英利能源有限公司、无锡尚德太阳能有限公司和晶科能源有限公司。在新增装机容量方面,根据国家可再生能源中心统计数据显示,由2008年以前的零增长发展到2012年的新增装机容量达328MW,仅次于德国和意大利,位列世界第三。这一趋还在以更快的速度增长。到2020年前后累计装机总量可达20000GW。国家电网公司《关于做好分布式光伏发电并网服务的工作的意见》中规定,自2012年11月1日起不超过6MW的光伏发电项目可以到当地的电网公司申请免费并网运行[1,3]。这一政策的颁布也促使了国内的光伏产业的快速发展。
在光伏发电量预测方面,我国华北电力大学栗然等结合当地气候特征模拟了30MW光伏电站发电量数据,利用支持向量机和回归分析法做了发电量的预测。但该方法仅模拟光伏发电站的预测数据,没有实验数据作为参考。华中科技大学在对18kW光伏发电站的研究中对每5分钟系统的发电量进行采集,陈昌松等结合这些数据和大量气象数据建立了基于相似日的神经网络预测模型。取得了很好的预测效果,但也同样存在着一旦环境急剧变化预测失真等情况[17]。
而在德国光伏发电量的预测已不仅仅在理论预测阶段,2009年就有6000MW光伏发电量在德国电网运行,RWE运输风暴公司(RWE TSO)与一些科研院在光伏发电量预测的准确性上做了深入研究,他们不仅能够准确的对光伏的发电量进行预测,更重要的是他们已经在考虑系统的平衡性、网络损耗、拥堵、储能等问题[18]。
总的来说,虽然我国的光伏发电量在以迅猛的速度发展,但由于我国的光伏产业起步较晚,也存在着很多因素制约着其发展,使得我国的光伏产业与国外的发达国家存在着一定差距。
5 光伏发电量预测的发展方向
随着光伏产业的大力发展,光伏发电量预测技术也日渐成熟。但是目前的研究方法过分依赖大量的原始数据及智能算法,而忽略了光伏阵列的电气特性以及影响光伏阵列输出功率的外在因素,因此,我们的预测工作仍有许多需要改进的地方。
光伏产业的飞速发展必将带来更多大规模的光伏发电站与大电网的并网,光伏并网后其输出功率的工程模型如式(1):
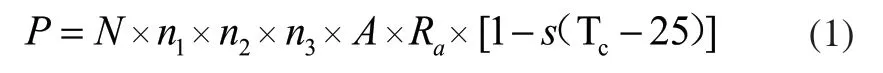
式(1)中P为光伏阵列的输出功率,N为光伏组建个数,n1为光伏转换效率,n2为最大功率点跟踪工作效率,n3为逆变器效率,A为光伏组件的面积,a为光伏阵列倾角,Ra为光伏阵列所受福照度,s为温度系数,Tc为光伏组件背板温度[6]。由此可见不仅温度和辐射强度对光伏发电量有影响,光伏阵列的安装角度等同样对光伏发电量存在一定的影响。由于目前光伏阵列的安装角度较为固定,尤其大型光伏发电站一旦安装很难更改。以往,光伏板的最佳安装角度都是根据太阳高度角来进行设置,而我国地理环境复杂,一些地区具有独特的气候特征,仅仅通过太阳高度角确定下来的安装角度不一定是最优的,因此,在安装角度上,我们可以综合考虑太阳高度角以及当地特有的气候特征,确定当地的最佳安装角度。
6 结束语
在对目前现有的大量有关光伏发电量预测的文献调研后,本文系统的将光伏发电量预测的方法归为数学统计预测法和人工智能预测法两大类。并相应地补充了其他有关光伏发电量预测的方法,起到了查漏补缺的效果,同时分析了各自的优缺点。数学统计法可以大致模拟出预测数据的变化趋势,但其过分依赖历史数据,存在预测结果滞后等特点。人工智能算法有很好的预测精度,也有很快的响应速度,但其理论性较强,多数情况下在计算机上进行建模与仿真,很难与大型光伏发电站的实际情况相结合。通过建立太阳能辐射模型的间接预测以及单纯的考虑光伏阵列的I/V特性预测同样存在实现起来过于复杂和考虑过于片面的缺点。未来光伏发电量预测技术应先在有的基础上加以改进完善,兼顾考虑环境因素、电气特性以及最佳安装角度等问题,实现预测精度更高、响应速度更快、考虑更为全面等特点。
[1]王磊.光伏发电系统输出功率短期预测技术研究[D].合肥工业大学,2012.
[2]Il-Song Kim,Myung-Bok Kim,Myung-Joong Youn.New Maximum Power Point Tracker Using Sliding-Mode Observer for Estimation of Solar Array Current in the Grid-ConnectedPhotovoltaic System[J].IEEE Transaction Industrial Electronice,2006,53(4):1027-1035.
[3]袁晓玲,施俊华,徐杰彦.计及天气类型指数的光伏发电短期出力预测[J].中国电机工程学报,2013,34:57-64,12.
[4]姜强鑫.基于小波神经网络的分布式光伏发电出力预测[D].南昌大学,2012.
[5]徐静,陈正洪,唐俊,李芬.建筑光伏并网发电系统的发电量预测初探[J].电力系统保护与控制,2012,18:81-85.
[6]李光明,廖华,李景天,赵恒利,黄波,何京鸿.并网光伏发电系统发电量预测方法的探讨[J].云南师范大学学报(自然科学版),2011,02:33-38,64.
[7]李光明,刘祖明,何京鸿,赵恒利,张树明.基于多元线性回归模型的并网光伏发电系统发电量预测研究[J].现代电力,2011,02:43-48.
[8]兰华,廖志民,赵阳.基于ARMA模型的光伏电站出力预测[J].电测与仪表,2011,02:31-35.
[9]杨超颖,王金浩,王硕,徐永海,黄浩.基于拟牛顿法小波神经网络的光伏发电系统短期功率预测模型[J].中国电力,2014,06:117-124.
[10]袁晓玲,施俊华,徐杰彦.基于BP神经网络的光伏发电短期出力预测[J].可再生能源,2013,07:11-16.
[11]姜侨娜,陈中.BP-马尔科夫组合预测方法在光伏发电量预测中的应用[J].电力需求侧管理,2011,06:21-24.
[12]张佳伟,张自嘉.基于PSO-BP神经网络的短期光伏系统发电预测[J].可再生能源,2012,08:28-32.
[13]李洪珠,贾威,聂苓,鄂小雪.基于鲁棒LS-SVM在光伏发电预测中的应用[J].计算机测量与控制,2013,05:1166-1167,1170.
[14]傅美平,马红伟,毛建容.基于相似日和最小二乘支持向量机的光伏发电短期预测[J].电力系统保护与控制,2012,16:65-69.
[15]Md Habibur Rahman,Susumu Yamashiro.Novel distributed power generating system of PV-ECASS using solar energy estimation[J].IEEE Transactions on Energy Conversion,2007,22(2):358-367.
[16]杨超,榑沼,弘贵.太阳能光伏发电系统发电量的预测方法[J].智能建筑电气技术,2011,02:29-34.
[17]李芬,陈正洪,成驰,段善旭.太阳能光伏发电量预报方法的发展[J].气候变化研究进展.2011,02:136-142
[18]Ernst B,Reyer,F,Vanzetta,J.Wind power and photovoltaic prediction tools for balancing and grid operation[J].2009 CIGRE/IEEE PES Joint Symposium.2009:1-9.

