航天器表面环境散射返回流TPMC模拟

靳旭红，黄 飞，程晓丽，王 强

（中国航天空气动力技术研究院，北京 100074）

文章编号：1001⁃246X（2015）05⁃0529⁃08

航天器表面环境散射返回流TPMC模拟

靳旭红，黄 飞∗，程晓丽，王 强

（中国航天空气动力技术研究院，北京 100074）

介绍试验粒子Monte Carlo（test particle Monte Carlo，TPMC）方法，并采用该方法对4种航天器表面出气分子形成的环境散射返回流进行数值模拟.其中，圆球出气表面的计算结果与已有的DSMC（direct simulation Monte Carlo）结果一致，验证了方法的正确性.此外，对不同出气和来流条件下圆形平板、凸半球和凹半球3种航天器简化表面出气分子形成的环境散射返回流进行计算，结果表明：出气表面外形是影响返回通量比的一个重要因素；圆形平板和凹半球出气表面的返回通量比远大于凸半球表面的；凹半球表面的出气分子会直接和出气表面碰撞形成直接流污染，且其量级远大于返回流污染.因此，在航天器设计中尽可能使用凸形表面作为敏感的出气表面可以有效降低出气分子污染.

出气分子；环境散射；返回流；试验粒子Monte Carlo方法；半球

0 引言

航天器表面的出气主要来自表面材料的放气、喷流控制、废气排放等［1］.在地球低轨道（轨道高度约为200km～400km）工作的航天器，其表面发出的气体分子由于和稀薄大气来流分子碰撞引起的散射效应，可能重新回到出气表面，形成返回流.返回流根据其产生机制分为自散射和环境散射，前者是由于出气分子之间发生碰撞导致其返回出气表面，后者是由于出气分子和来流分子之间发生碰撞而形成的，前者在量级上远小于后者［2］.衡量返回流大小的物理量是返回通量比（return flux ratio，RFR），定义为返回出气表面的分子数与总出气分子数的比值.一般地，返回通量比很小，但也会严重影响航天器上某些外部敏感装置的性能.例如，卫星的太阳能电池板、透镜和反射镜等光学表面对工作环境极其敏感，极小量的返回流污染也会严重影响其性能［3］.比如，太阳能电池板表面的返回流污染会降低其透射率，导致太阳能转化为电能的效率减小；透镜或反射镜等光学表面的返回流污染也会降低其透射率或反射率，导致测量精度下降.在很多情况下，这些装置的性能决定着整个卫星的总体性能［4］.而且，航天器一般设计成使敏感表面之间的视线因子达到最小，从而直接流污染量最小，大部分出气分子离开出气表面后直接进入宇宙空间，导致环境散射返回流成为最大的污染源之一.因此，在航天器设计中必须对环境散射返回流表面累积污染进行精确的预测和控制［5］.

环境散射流的各向异性导致处理其引起的污染问题存在诸多困难.常见的分析方法，如Bhatnager⁃Gross⁃Krook（BGK）模型和DSMC（direct simulation Monte Carlo）方法在这个问题上都显得低效，前者因分析过于复杂而无法应用于工程，后者则需要耗费巨大的计算时间和存储量［4］.试验粒子Monte Carlo（test particle Monte Carlo，TPMC）方法是一种随机模拟方法，适用于无碰撞或近自由分子流区的气体流动［6］.它区别于DSMC方法的明显特点是仿真分子是顺序而非同时产生的，一次只产生一个试验粒子，因此不会耗费太多的计算时间和存储量，更适用于复杂边界导致的多重表面反射流动问题［7］.Fan等［2］首次将TPMC方法用于简单航天器表面出气导致的自散射和环境散射返回流问题.Guo和Liaw［8］也做了类似的研究，表明TPMC方法相比于DSMC方法可节省大量的计算时间，又比BGK模型的结果精确，从而在航天器表面污染预测中更实用.特别地，据作者所知，国内尚无人实现TPMC方法在稀薄气体动力学领域的应用.

首先以圆球表面出气分子形成的环境散射返回流问题为例，简要介绍TPMC方法的模拟过程，然后采用该方法对4种航天器简化表面（图1）出气分子形成的环境散射返回流进行计算.在圆球表面方法验证的基础上，在不同出气和来流条件下对圆形平板、凸半球和凹半球等3种简化表面出气分子形成的环境散射返回流进行计算和对比，分析不同航天器表面外形对返回通量比的影响，为航天器设计中减小返回通量比提供理论参考.

图1 环境散射返回流流动示意图Fig.1 Schematic of ambient⁃scattered flux flows

1 TPMC模拟方法

Monte Carlo方法，或称计算机随机模拟方法，是一种基于“随机数”的计算方法.该方法源于美国在第一次世界大战后研制原子弹的“曼哈顿计划”.Ulam和该计划的主持人之一、数学家冯·诺伊曼（J.von Neumann）用驰名世界的赌城——摩纳哥的Monte Carlo——来命名这种方法.TPMC方法是一种利用试验粒子来模拟稀薄气体分子运动的计算机随机模拟方法，每个试验粒子代表大量的气体分子，代表真实分子的试验粒子顺序进入计算域，其速度是自由来流质量速度和分子热运动速度的矢量和.作为一类随机模拟方法，TPMC方法具有传统方法所没有的优点：不存在收敛性问题，只要试验粒子数量足够大，计算结果一定收敛；计算量和复杂性不随问题的维数呈指数增长，可以很好地解决科学计算中的“维数灾难”问题.而且，相对于DSMC方法，TPMC方法的仿真分子是顺序而非同时产生的，不会耗费太多的计算时间和存储量.

假设出气和来流分子均满足单组元弹性硬球模型，遵循Maxwell速度分布；出气分子离开表面时满足各向同性余弦规律分布且自散射和环境散射过程解耦.TPMC方法的主要步骤可以概括为：首先，构建一个足够大的控制体并在出气表面产生一个试验粒子；然后，跟踪和模拟该试验粒子之后的运动轨迹和碰撞过程，直到其飞出控制体或出气表面；最后，重复上述过程直至试验粒子数足够大，以保证计算结果收敛，统计计算返回通量比.

1.1 构建控制体

对于圆球环境散射返回流问题，控制体为一个假想的与出气球面同心的圆球体，其半径

其中，rb为圆球表面半径，K为一个确定控制体尺寸的正参数．控制体尺寸既要保证足够大不影响计算结果的准确度，又不至于过度增加计算量．文献［9］经验证发现K＝30时可以忽略控制体外的分子运动对返回流的影响，获得统计上足够稳定的结果.

1.2 产生试验粒子

试验粒子的初始位置根据概率分布函数求逆法确定［10］.设初始位置在球坐标系中表示为（r，θ，φ），由于出气表面为一个球面，且球坐标系的原点在该出气球面的球心，显然有

设二维随机变量（θ，φ）的联合概率密度函数为f（θ，φ），则其在（θ，φ）和（θ＋dθ，φ＋dφ）区间的概率为

则

其满足归一化条件，即

对变量θ，φ分别将联合概率密度函数在另一变量的取值范围内积分，可得对应的边际概率密度函数，即

进而可得边际概率分布函数分别为

根据随机变量的概率分布函数服从（0，1）区间的均匀分布［11］，可令Fθ（θ）＝R1，Fφ（φ）＝R2，其中R1，R2为（0，1）区间均匀分布的随机数（下文中Ri（i∈N，i≥3）亦为（0，1）区间均匀分布的随机数），即

综上，试验粒子的初始位置为

试验粒子的初始速度vb满足Maxwell速度分布，其表达式可根据通过某表面的分子数通量推导出，在球坐标中的分量形式为

式中vmb＝2kTb/mb为最可几热运动速度，且k＝1.38×10－23J·K－1为Boltzmann常数，Tb为出气表面温度，mb＝Mbm0为出气分子质量，Mb为出气相对分子质量，m0＝1.67×10－27kg为原子质量单位.

同样根据分子动理学，试验粒子在初始位置的局部分子自由程λ满足指数分布［12］，即

其中，λb为出气条件下的分子平均自由程，表达式为［8］

函数χ（x）定义为

且

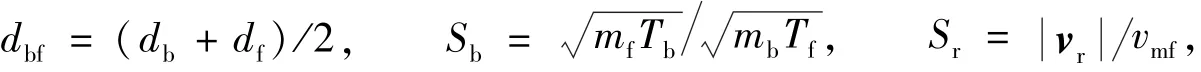
式中，nf为来流分子数密度，db为出气分子直径，df为来流分子直径，Tf为来流温度，mf＝Mfm0为来流分子质量，Mf为来流相对分子质量，vf为来流速度，vmf＝2kTf/mf为来流温度对应的最可几热运动速度，vr＝vb－vf为碰撞前相对速度矢量.

1.3 二体弹性碰撞

根据二体弹性碰撞理论［13］，分子碰撞前后的相对速度大小不变，方向是各向同性的，故碰撞后的相对速度v∗r在球坐标中的分量形式为

于是，试验粒子碰撞后的速度为

式中，vm为两个碰撞分子的质心速度，表达式为

1.4 统计返回通量比

根据Monte Carlo方法的方差理论，产生并跟踪足够多的试验粒子之后，返回通量比一定会收敛.记Ns为试验粒子总数，Nr为返回出气表面的试验粒子数，则标准偏差为1/Ns，且返回通量比为

2 圆球表面环境散射返回流验证

考虑圆球表面出气分子形成的环境散射返回流问题，以其作为验证算例.不失一般性，采用的出气和来流条件如表1所示.图2是不同出气和来流条件下返回通量比，DSMC计算结果取自文献［1］.由图可见，随着出气表面半径、来流分子数密度、来流速度的增加，RFR近似呈线性增大；随着出气表面温度的增加，RFR近似呈非线性减小.本文的TPMC计算结果和DSMC计算结果符合较好，尤其是RFR随来流分子数密度的变化关系两者几乎一致.当然，两者之间也存在较小的偏差，尤其是出气表面半径、来流速度较大，以及出气表面温度较低和较高时.产生微小偏差的原因有2个：一方面，两种方法都属于随机模拟方法，必然存在统计误差；另一方面，图2中的DSMC曲线是文献［1］根据返回流的输运特性和DSMC模拟结果拟合出的公式，拟合过程中难免引入误差.

表1 计算条件Table 1 Com putational parameters

图2 不同出气和来流条件下圆球表面环境散射返回通量比Fig.2 RFR of flows past a sphere at different outgassing and freestream conditions

3 三种航天器简化表面环境散射返回流

考虑现代航天器常见的三种简化表面，即圆形平板、凸半球、凹半球表面，采用TPMC方法计算其出气分子形成的环境散射返回流，分析不同表面外形所受影响.

3.1 不同出气条件情形

图3是三种简化表面的RFR随出气表面半径、出气表面温度，以及出气相对分子质量平方根的变化曲线，不同表面外形的RFR变化趋势相同，但存在定量差异.

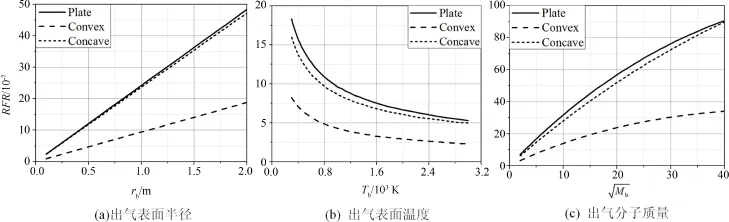
图3 不同出气条件下三种简化表面环境散射返回通量比Fig.3 RFR of flows past a circle flat plate，a convex and concave hemisphere at different outgassing conditions

图4 不同来流条件下三种简化表面环境散射返回通量比Fig.4 RFR of flows past a circle flat plate，a convex and concave hemisphere at different freestream conditions

类似于上节圆球表面的情形，对于出气表面半径，RFR随其增加呈线性增大；对于出气表面温度，RFR随其增加近似呈非线性减小.特别地，在较小Tb范围，RFR减小剧烈；在较大Tb范围，则减小缓慢并趋于稳定值.另外，对于出气相对分子质量平方根，RFR随其增加近似呈抛物形增大.

值得注意的是，在所有出气条件下，圆形平板和凹半球出气表面的返回通量比都远大于凸半球出气表面的，并且圆形平板的出气表面的返回通量比只略高于凹半球表面的.然而，对于凹半球出气表面，部分出气分子会直接撞到出气表面形成直接流污染，衡量直接流大小的物理量是直接通量比 （direct flux ratio，DFR），定义为直接撞到出气表面的分子数与总出气分子数的比值.若出气分子离开表面时满足各向同性余弦规律分布，则DFR可采用表面之间的视线因子法确定［4］.对于凹半球出气表面，容易求出DFR为0.5，远大于相应的RFR，后者约为10－6的量级.

3.2 不同来流条件情形

取来流条件为来流分子数密度、来流速度、来流相对分子质量、来流攻角，以及来流温度.设简化表面垂直放置，则来流攻角定义为来流速度矢量与简化表面内法向的夹角.

图4是三种简化表面的RFR随来流分子数密度、来流速度、来流相对分子质量，以及来流攻角的变化曲线.像不同出气条件情形一样，不同表面外形的RFR变化趋势也相似，但存在定量差异.

同样类似于上节圆球表面，对于来流分子数密度和来流速度，RFR随其增加近似呈线性增大.与此不同，对于来流相对分子质量，RFR随其增加呈非线性增大.特别地，在较小Mf范围，RFR增大得剧烈；在较大的Mf范围，RFR增大得缓慢并趋于稳定.RFR相对于来流攻角的变化曲线关于αf＝0°对称，且当αf从－90°增加到90°时，RFR先增大后减小.

图5 不同来流温度下三种简化表面环境散射返回通量比Fig.5 RFR of flows past a circle flat plate，a convex and concave hemisphere at different freestream temperature

图5是三种简化表面的RFR随来流温度的变化曲线及其局部放大图，近似呈微小线性增大，表现为拟合直线的斜率很小.同出气条件情形，在所有来流条件下，圆形平板和凹半球出气表面的返回通量比基本都远大于凸半球出气表面的，并且圆形平板的出气表面的返回通量比大多只略高于凹半球出气表面的.同样地，凹半球出气表面也存在直接流污染问题，并且其量级远大于对应的返回流污染.

三种简化航天器出气表面的RFR相对于每一个出气或来流条件的变化趋势都存在相似性，其内在原因是出气和来流条件影响返回通量比的物理机制.作者已在文献［9］中采用分子动理学的观点分析过，概括如下.返回通量比的大小直接受两个因素的影响，出气和来流分子的碰撞频率以及碰撞后出气分子的速度偏转角.碰撞频率和速度偏转角越大，越有利于出气分子返回出气表面，返回通量比就越大.每个出气和来流条件都是通过控制碰撞频率或速度偏转角中的1个或2个参数来影响返回通量比的.

4 结论

以圆球表面出气分子引起的环境散射返回流问题为例，介绍了TPMC方法的模拟过程，采用该方法对四种航天器简化表面的环境散射返回流进行数值模拟，分析出气和来流条件的影响.结论如下：

1）对于圆球表面出气分子形成的环境散射返回流问题，TPMC结果和已有的DSMC结果符合很好，验证了该方法的可靠性.

2）除了出气和来流条件，几何外形也影响返回通量比.圆形平板、凸半球和凹半球这三种简化出气表面的RFR相对于每一个出气或来流条件的变化趋势存在相似性，其内在原因是出气和来流条件影响返回通量比的物理机制.

3）出气表面半径为1m～3m的航天器，在典型的低轨道环境下（轨道高度约为200km～400km），RFR为10－6的量级.所有出气和来流条件下，圆形平板和凹半球出气表面对应的RFR都远大于凸半球出气表面的；圆形平板出气表面的RFR大多略高于凹半球表面的.

4）对于凹半球表面，部分出气分子会直接撞到出气表面形成直接流污染，且DFR为0.5，远大于RFR.因此，在航天器设计中尽可能使用凸形表面作为敏感出气表面可以有效减小出气分子污染.

［1］ Bird G A.Spacecraft outgas ambient flow interaction［J］.Journal of Spacecraft，1981：31－35.

［2］ Fan C，Gee C，Fong M C.Monte Carlo simulation ofmolecular flux on simple spacecraft surfaces due to self⁃and ambient⁃scatter of outgassingmolecules［R］.AIAA Paper 93－2867，1993.

［3］ Tribble A C，Boyadjian B，Haffner J，McCullough E.Contamination control engineering design guidelines for the aerospace community［R］.NASA CR 4740，1996.

［4］ Lee JW，YiM Y.Modified view factor method for estimating molecular backscattering probability in space conditions［J］Journal of Thermophysics and Heat Transfer，2006，20（2）：336－341.

［5］ Justiz C R，Sega R M，Dalton C，Ignatiev A.DSMC⁃and BGK⁃based calculations for return flux contamination of an outgassing spacecraft［J］.Journal of Thermophysics and Heat Transfer，1994，8（4）：802－803.

［6］ Davis D H.Monte Carlo calculation ofmolecular flow rates through a cylindrical elbow and pipes of other shapes［J］.Journal of Applied Physics，1960，31（11）：69－76.

［7］ Bird G A.Monte Carlo simulation of gas flows［J］.Annual Review of Fluid Mechanics，1978：11－31.

［8］ Guo K L，Liaw G S.Outgassing⁃ambient interaction of a spherical body［R］.AIAA Paper 94－2063，1994.

［9］ Jin X H，Huang F，Cheng X L.Test particle Monte Carlo simulation of return flux due to ambient scatter of outgassing molecules［C］.The 29th International Symposium on Rarefied Gas Dynamics，Xi’an，China，July 13－18，2014.

［10］ 沈青.稀薄气体动力学［M］.北京：国防工业出版社，2003：284－288.

［11］ 茆诗松，程依明，濮小龙.概率论与数理统计教程［M］.北京：高等教育出版社，2011：122－128.

［12］ 李椿，章立源，钱尚武.热学［M］.第二版.北京：高等教育出版社，2008：87－91.

［13］ Bird G A.Molecular gas dynamics and the direct simulation of gas flows［M］.Oxford：Oxford University Press，1994：30－45.

Test Particle M onte Carlo Simulation of Return Flux on Spacecraft Surfaces due to Ambient Scatter of Outgassing M olecules

JIN Xuhong，HUANG Fei，CHENG Xiaoli，WANG Qiang （China Academy of Aerospace Aerodynamics，Beijing 100074，China）

Test particle Monte Carlo（TPMC）method is presented.Return flux on four geometric surfaces due to ambient scatter of outgassingmolecules is simulated.Return flux ratio（RFR）obtained for flow past a sphere is in good agreementwith DSMC results. RFR on outgassing and freestream conditions for flows past three geometric bodies，including a circle flat plate，a convex and concave hemisphere，is investigated.RFR for flows past a circle flat plate and a concave hemisphere ismuch greater than that for flows past a convex hemisphere.Outgassingmolecules collide on outgassing surfaces directly forming direct flux contamination for flows past concave surfaces，which is much greater than RFR.Thus，using convex outgassing surfaces in spacecraft design can decrease return flux contamination effectively.

outgassingmolecules；ambient scatter；return flux；test particle Monte Carlo；hemisphere

V211.25

A

2014－09－27；

2015－02－03

靳旭红（1988－），男，硕士研究生，主要从事稀薄气体流动研究，E⁃mail：jinxuhong08＠163.com∗通讯作者：黄飞（1982－），高级工程师，E⁃mail：huang05013＠163.com

Received date： 2014－09－27；Revised date： 2015－02－03