SymmSketch:Creating symmetric 3D free-form shapes from 2D sketches

Yongwei Miao(),Feixia Hu,Xudong Zhang,Jiazhou Chen,and Renato Pajarola

©The Author(s)2015.This article is published with open access at Springerlink.com

SymmSketch:Creating symmetric 3D free-form shapes from 2D sketches

Yongwei Miao1(),Feixia Hu1,Xudong Zhang1,Jiazhou Chen1,and Renato Pajarola2

©The Author(s)2015.This article is published with open access at Springerlink.com

ThispaperpresentsSymmSketch-a system for creating symmetric 3D free-form shapes from 2D sketches. The reconstruction task usually separates a 3D symmetric shape into two types of shape components,that is,the self-symmetric shape component and the mutual-symmetric shape components.Each type can be created in an intuitive manner.Using a uniform symmetry plane,the user first draws 2D sketch lines for each shape component on a sketching plane.The z-depth information of the hand-drawn input sketches can be calculated using their property of mirror symmetry to generate 3D construction curves.In order to provide more freedom for controlling the local geometric features of the reconstructed free-form shapes(e.g.,non-circular crosssections),our modeling system creates each shape component from four construction curves.Using one pair of symmetric curves and one pair of general curves,an improved cross-sectional surface blending scheme is applied to generate a parametric surface for each component.The final symmetric free-form shape is progressively created,and is represented by 3D triangular mesh.Experimental results illustrate that our system can generate complex symmetric free-form shapes effectively and conveniently.

3D reconstruction;construction curves; free-form shapes; mirror symmetry; sketch-based modeling

1 Introduction

In computer graphics and digital entertainment, sketching,which was an important art genre in the early community[1],is still a common way to convey ideas quickly.Sketch-based modeling is a popular research topic for the creation of 3D models due to its natural and straightforward manner to represent real world objects[2-4].

Many studies have shown that inferring a free-form shape from line drawings is very difficult[5].Many sketch-based modeling systems have been proposed, such as SKETCH[6],Teddy[7],ShapeShop[8], SmoothSketch[9],FiberMesh[10],ILoveSketch[11], Rigmesh[12],Sketch2Scene[13],and ArtiSketch[14]. However,many shape modeling operations in these sketch-based systems are performed in 3D object space.A rough 3D model is first created,and new features can then be added interactively in a progressive way using some special operations, such asextrusion,cutting,rotation,merging, deformation,etc.

From the viewpoint of practical applications, sketch-based modeling provides a very popular approach for interactively generating 3D shapes[2]. It can offer the user a simple way to access and interpret 3D objects,and thus can effectively avoid the tedious processes associated with professional 3D modeling software.Moreover,due to the symmetry properties of many real-world objects, it is useful to provide the user with a sketchbased reconstruction system which works for 3D symmetric shapes[15-18].Traditional techniques for modeling symmetric objects from two construction lines are limited to mirror-symmetric shapes with circular cross-sections[19,20].In order to provide more freedom for controlling the local geometricfeatures of reconstructed free-form shapes(e.g.,noncircular cross-sections),we present SymmSketcha novel system for creating symmetric complex 3D shapes from 2D sketches.Using the symmetry information in the 2D input sketches(see Fig.1(a)), 3D symmetric construction curves can first be computed.3D asymmetricgeneralconstruction curves can then be calculated from the symmetric ones(see Figs.1(b)and 1(c)).Each shape component can be generated from a pair of symmetric curves and a pair of general curves,and the complex symmetric 3D free-form shapes can finally be created(see Figs.1(d),1(e),and 1(f)).

The main contributions of our work can be summarized as follows:

·A progressive method to create symmetric 3D free-form shapes that consist of two types ofshapecomponents:self-symmetricshape components,and shape components that are symmetrically related to another shape with respect to a symmetry plane.

·A computational theory to recover z-depth information for 3D construction curves which combine a pair of symmetric construction curves and a pair of asymmetric(general)construction curves.

·An improved cross-sectional surface blending scheme to generate each shape component of a symmetric 3D shape;the cross sections need not be circular.

Fig.1 Example of a complex symmetric dog model created by our SymmSketch system.(a)shows the user input handdrawn 2D sketches. (b)and(c)are two different views of the corresponding 3D construction curves generated by our approach.(d)-(f)show the final created 3D free-form shapes in three different views.

The rest of the paper is organized as follows. Related work is reviewed in Section 2.Section 3 explains our z-depth computation approach for generating 3D construction curves.A description of our free-form objects modeling system is given in Section 4.Section 5 shows experimental results and comparisons with existing methods.Section 6 concludes the paper and suggests some future work.

2 Related work

To create 3D free-form shapes,designers tend to directly express their design ideas in 2D sketches, and the system should correctly interpret the input sketches to generate the final 3D shapes[21,22]. Based on a single input 2D line drawing,many 3D object reconstruction algorithms have been proposed.Here,we only review previous work concerning sketch-based modeling approaches for 3D free-from shapes.The readers may refer to the surveys[2]and[5]and the references therein for other related techniques.

Many researches consider 3D free-from object reconstruction starting from visible and hidden details in 2D sketches of the underlying shape[6, 7].Given an interactive input of 2D free-form strokes,the Teddy system[7]provides the user a sketching interface for easily designing free-form objects and constructing plausible 3D polygonal meshes.Using sketched 2D outlines of 3D objects, Schmidt et al.[8]developed the ShapeShop system that can create the solid models using hierarchical implicit volume models,BlobTrees.Karpenko and Hughes[9]proposed SmoothSketch,a system for inferring plausible complex free-form shapes from a wide class of visible-contour sketches.The FiberMesh system[10]presented by Nealen et al.is also a free-form shape design system which can reconstruct 3D objects from a collection of input curves.Using a non-linear optimization framework, FiberMesh can automatically generate a smooth surface with sharp creases and darts that are controlled by the userinputstrokes.Bae et al.[11]presented the 3D curve sketching system ILoveSketch which allows professional designers to design conceptual 3D curved models in an easy pencil-and-paper way.By unifying the modeling and rigging stages of the 3D character animationpipeline,the RigMesh system [12]provides an easy-to-use interface for generating complex 3D rig characters.By performing sketch-based co-retrieval and co-placement of 3D relevant models,Xu et al.[13]presented a Sketch2Scene system which can automatically turn input 2D freehand sketches into semantically valid and well arranged 3D scenes.The ArtiSketch system[14]can reconstruct articulated 3D objects from several articulated 2D sketches, and novel poses of the 3D model can be generated by manipulating the model skeletons.By employing a Laplacian framework for sketch-based editing, Nealen et al.[23]provided an intuitive interface for the user to edit shape silhouettes or create sharp features on 3D triangular meshes.

However,due to the lack of depth information in the input 2D sketches,the object reconstruction process is non-deterministic and the final generated 3D object cannot be unique[24].To overcome these difficulties,many recent solutions add constraints to the original sketches[19,25]or match sketches to existing 3D models using an evocative system[26-28].Li et al.[29]proposed a modeling system for generating piecewise planar 3D objects from object edges drawn on the input image.Using optimization of 3D information,Wang et al.[30]developed an approach for creating curved objects from single 2D line drawings.Xue et al.[31]presented a 3D modeling approach for recovering regular geometry from a single image of a symmetric object.Chen et al.[32]also introduced an interactive 3-sweep technique for extracting simple man-made editable objects from an input image.The 3D shapes reconstructed by these methods are comparatively simple and are restricted to some specific class of objects.Andre et al.[20]presented a simple 3D reconstruction scheme in which each object part can be constructed from two construction lines.However,much user interaction is needed to reconstruct complex objects correctly because their method has no information of the relative depths of multiple parts.

Cordier et al.[19]exploited mirror symmetry to create 3D models;extra operations are not needed to assemble shape components.Actually,the symmetry assumption is one of the least restrictive for 2D sketches due to the fact that many realworld 3D objects,such as animals,buildings, and many other organic structures,exhibit certain kinds of symmetry[15-17].Under orthographic or perspective projection,the 3D structure of a shape with certain kinds of symmetry can fully be reconstructed as long as one can determine the symmetric pairs[18].Using hand-drawn input sketches of bilaterally symmetric objects,¨Oztireli et al.[33]presented a 3D modeling algorithm based on a set of planar curves.Using a set of mirrorsymmetric curves,Cordier et al.[34]also introduced a 3D reconstruction method for generating some particular types of wire-frame objects.

The aim of our modeling system is to use natural modeling techniques to generate symmetric complex free-form objects from user input sketches. Traditionaltechniquesformodeling symmetric objects are limited to generating simple 3D shapes with circular cross-sections due to the reconstruction scheme which uses only two construction lines[19]. Compared with such traditional modeling systems, the most important difference of our SymmSketch system is that each shape component is generated from four construction curves,a pair of symmetric curves and a pair of asymmetric general curves which provide more freedom to control the local geometric features of the final 3D free-form shapes,including non-circular cross-sections.

3 Z-depth computation for construction curves

3.1 Definitions and assumptions

To clarify the use of hand-drawn input sketches for generating 3D construction curves,some definitions commonly used in practical applications are given and some assumptions are also presented to simplify the 3D reconstruction process.The reader should refer to Fig.2.

The sketching plane is a plane on which the user can draw 2D sketch lines interactively.Without loss of generality,the sketching plane can be selected as the XOY plane z=0.The user input 2D sketches on the sketching plane can thus be considered as the orthogonal projections of the construction curves of a 3D shape.In our modeling system,only one sketching plane is adopted because it is difficult and inconvenient to draw several overlapping strokes belonging to different components,projected ontodifferent planes.

Fig.2 Z-depth computation for construction curves of one self-symmetric shape component.

The symmetry plane is a special plane with respect to which the mirror-symmetric shape components exhibit their property of symmetry. Symmetric free-form shapes are invariant under reflection in their symmetry plane.Our modeling system is designed to use only a single symmetry plane for reconstructing the whole 3D shape.

Symmetric curvesareuserinputsketches whose corresponding 3D construction curves are symmetric with respect to the symmetry plane.Each point sampled on these sketched curves is called a symmetric point.Here,the property of symmetry holds for the curves in 3D space rather than for the projected ones on the sketching plane.This is because a curve which is mirror-symmetric in 3D space may not be mirror-symmetric if projected to a 2D plane.

Generalcurvesareuserinputasymmetric general sketches for representing shape components. Each point sampled on these general curves is called a general point.

Construction curves are 3D curves in 3D space that are recovered from the symmetric or general inputsketchesusing ourz-depth computation approach.We assume that each component of the reconstructed complex shapes are generated from four construction curves:two symmetric and two asymmetric general construction curves.

To effectively reconstruct complex free-form shapes,unlike traditional methods[19,20],our modeling system generates each component of a free-form object by taking four sketches on the sketching plane as input.When the user draws the 2D sketches on the sketching plane,each sketch curve is uniformly sampled with an equal number of sample points and lifted up to a 3D construction curve after determining the z-coordinates of these sample points.To reconstruct a complex 3D freeform shape,the four corresponding construction curves are processed simultaneously,and the zdepth information of the construction curves can be calculated using the property of mirror symmetry. In particular,two corresponding recovered symmetry points of two symmetric construction curves must be mirror-symmetric with respect to the symmetry plane,whilst the vector connecting the two recovered symmetric points is perpendicular to the vector connecting the two corresponding recovered general points.

For simplicity, the input sketches can be considered to be the orthogonal projections of 3D construction curves onto the XOY sketching plane. The x and y coordinates of vertices on the input sketches can simply be taken as the coordinates of the corresponding reconstructed 3D vertices(see Fig.2).Thus the main remaining problem of 3D object reconstruction is the estimation of the z coordinates of the object vertices.

3.2 Z-depth computation approach

In order to create symmetric complex free-form objects,wesupposethateach 3D shapecan be separated into two types of components:selfsymmetric shape components,and mutual pairs of symmetric shape components with respect to a unique predefined symmetry plane.For each point on the surface of a self-symmetric component,there is a symmetric corresponding point locating on the same component.For each point on one of the mutuallysymmetric components,there is a corresponding symmetric point on the other component.Using the user input sketches for these two types of shape components,the z-coordinate information of the construction curves can be determined by two different schemes,based on the property of mirror symmetry.

3.2.1 Z-depth computation for selfsymmetric components

Due to the property of mirror symmetry,the z coordinates of sample points on the symmetric curves and general curves of a self-symmetric shapecomponent can be calculated as follows.

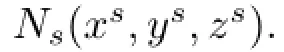
Given the symmetry plane Πsas shown in Fig.2, we choose one pair of symmetric verticeson the symmetric curves and one pair of general verticeson the general curves located on the symmetry plane Πs.The dashed lines connecting vsito,andto,intersect at one point.Thus, the following equations link these four points:

where Ngis a vector perpendicular to the vector Ns.Using the coordinates of the vertices,these four equations can be expressed as follows:

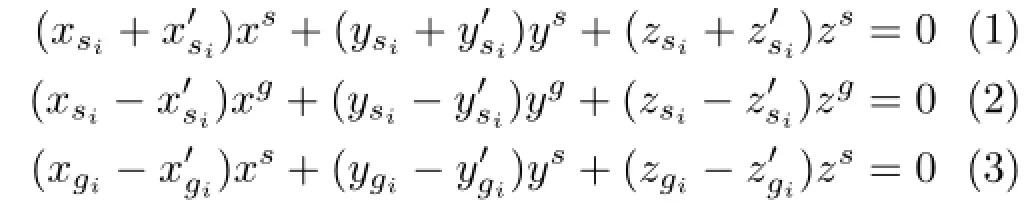
and

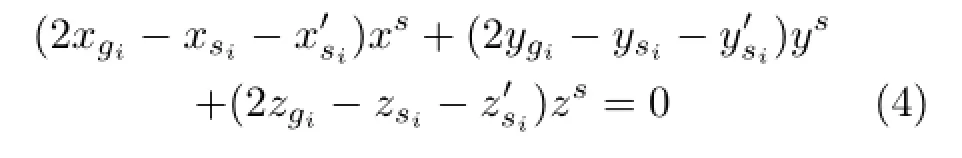
By combining Eqs.(1)and(2),the z-coordinatesof the symmetric pointscan be calculated as follows:

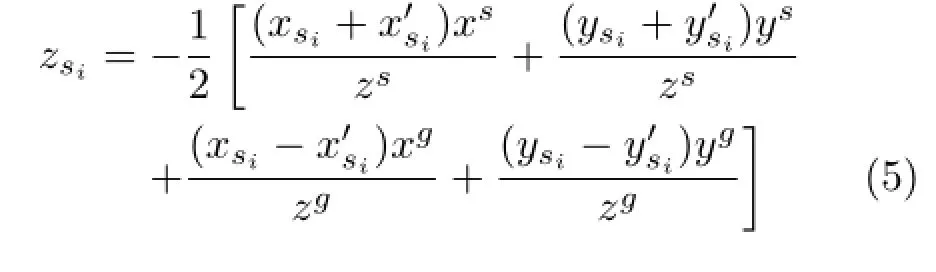
Finally,by combining Eqs.(3)-(6),the z-coordinatesof the general pointscan be determined as follows:

3.2.2 Z-depth computation formutuallysymmetric components

Ifoneshapecomponentisrelated by mirror symmetry to another component of the same object (see Fig.3),the z coordinates of the sample points on two pairs of symmetric curves can be easily obtained using Eqs.(5)and(6).Thus,the z-depth information of the sample points on only one pair of the general curves needs to be computed using Eqs. (7)and(8),and that of the other pair of general curves can be easily determined using the property of mirror symmetry.For example,for a general point vgi(xgi,ygi,zgi)sampled from the general curves(on the blue curve in Fig.3),the symmetrically related

Fig.3 Z-depth computation for construction curves of two mutually-symmetric components of the same object.

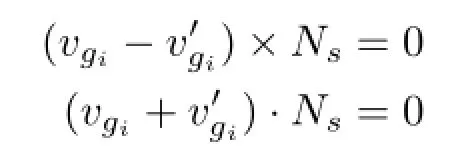
so

By combining Eqs.(9)-(11),the coordinate of the general pointcan be calculated as follows:

Next,we show how the above z-depth computation approach is used by our SymmSketch system to create symmetric complex free-form shapes.

4 3D reconstruction of symmetric free-form shapes

To reconstruct symmetric 3D shapes,Cordier et al.[19]only used two symmetric curves which result in the final shape consisting of cylinderlike components with circular cross-sections.Their method can only generate relatively simple 3D shapesdueto itslimitation to workingfrom only two symmetric curves.The motivation of our work is to provide more freedom to control the reconstructed shape to meet specific geometric requirements and artistic wishes.By adopting a pair of symmetric construction curves and a pair of general construction curves,our modeling system can create complex free-form shapes with relatively flat or more curved components.In this section, we discuss how to classify the user’s input sketches and determine the four construction curves for each shape component.Furthermore,using the 3D construction curves,we also describe how to generate a complex mirror-symmetric 3D free-form shape.

4.1 Overview of our object reconstruction algorithm

Taking the planar sketches that contain symmetric and general curves as input,3D coordinates of the sample points can be recovered by using the zdepth computation in Section 3.The final output 3D symmetric free-form shapes are created and represented as triangular meshes. The high-level framework of our 3D reconstruction algorithm can be summarized as follows.

Step 1:Discretization of 2D sketching lines. After the user draws the 2D sketches on the sketching plane,our modeling system automatically discretizes the input sketches as polygons whose vertices are uniformly sampled on the smooth quadratic B-spline curves that interpolate the input sketch points. Each pair of symmetric or general curves is stored successively according to the order in which the user draws them.

Step 3:Generation of parametric surfaces using a cross-sectional blending scheme.Given one pair of 3D symmetric construction curves and one pair of 3D general construction curves,an improved cross-sectional surface blending scheme is applied to generate a parametric surface for each shape component.The final complex free-form shapes are progressively generated and may comprise several shape components.

4.2 Discretization of 2D sketching lines

As shown in Fig.2,under orthogonal projection, the user interactively sketches 2D symmetric or general curves for each shape component on thesketching plane.Following Blair’s scheme[1]for illustrating shapes using several profiles,for each selfsymmetric component,the user should sketch a pair of symmetric curves,and then draw a pair of general curves(see Figs.4(a)-4(d)).These four curves usually connect at their endpoints.For two mutualsymmetric shape components,the user sketches two pairs of symmetric curves for both components and then draws the pairs of general curves for each component respectively(see Figs.4(e)-4(h)).Each pair of mutually-symmetric curves on these two components usually have no common connection at their endpoints.

Asthey areinput,thesketchesarestored with a unique index denoting the order in which they are drawn.Thus,each pair of symmetric or general curves is handled together.Each pair of general curves is coupled with the corresponding symmetric curves.Sketch vertices are automatically uniformly sampled from the sketched curves which are represented as quadratic B-spline curves interpolating the sketch inputdata [35].For simplicity,each pair of sketch curves is sampled using the same number of sample points.How we then perform z-depth recovery is outlined in the next section.

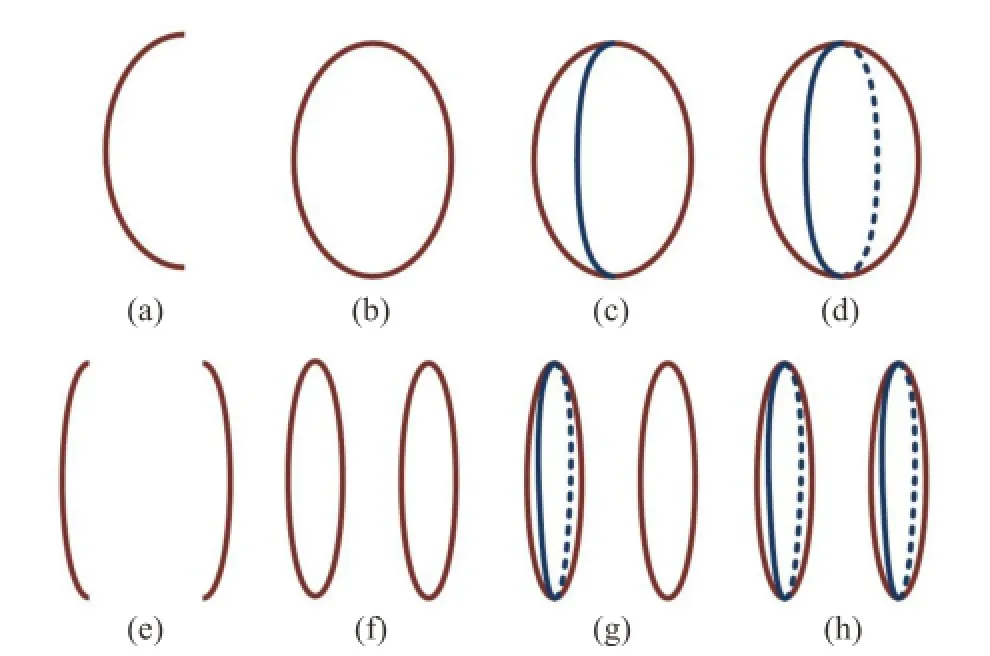
Fig.4 Interactively sketching shape components step by step. (a)-(d)show the drawing order when sketching a self-symmetric shape component in 2D,and(e)-(h)illustrate the drawing order for mutually-symmetric components.

In general,to be able to reconstruct free-form objects effectively,there must be an even number of nodes stored in Lq.Nodecontains two pairs of symmetry curves depicting two shape components, whilst nodestores two pairs of general curves representing two shape components.If this requirement is not met,the modeling system will ask the user to redraw the sketched curves.

The different types of nodes in Lpand Lqrequire different computational schemes to recover the zdepth information of the vertices sampled on their sketch curves.

·To create the self-symmetric shape component from a node Ipi∈Lp,the system first calculates the z coordinates of the symmetric points using Eqs.(5)and(6).The z coordinates of the general points are then computed from the 3D symmetric points using Eqs.(7)and(8).

·To create two mutually-symmetric shape components from nodes Iq2j,Iq2j+1∈Lq,we note that node Iq2jcontains two pairs ofsymmetric curves whose corresponding construction curves may be computed using Eqs.(5)and(6).The generated symmetric construction curves are re-paired so that two pairs of symmetric curves are re-inserted into Iq2jand Iq2j+1respectively(see Fig.5).Each node Iq2jand Iq2j+1contains one pair of symmetric construction curves and one pair of general curves.The z coordinates of the general points of Iq2jcan be calculated from the symmetric ones in the same node using Eqs.(7) and(8).The general curves of Iq2j+1are finally treated as a symmetric image of the general curves of Iq2j,and their z-depth information is computed using Eqs.(12)-(14).

Fig.5 Re-pairing the input symmetric and general sketches.

An example of our procedure for re-pairing and re-inserting different sketches is given in Fig.5.The head,body,and tail of the doll are self-symmetric, so is each represented by four sketch curves in Ipirespectively.For the mutually-symmetric ear parts,following the drawing order,initially the four symmetric curves for depicting the two ears are stored in one node and the four general curves are stored in another node(see the top right figure of Fig.5).After the re-pairing step,each pair of symmetric curves is separated into two nodes respectively,and the symmetric curves for the two ears are included in Iq2jand Iq2j+1respectively(see the down right figure of Fig.5).

As a result,all 3D coordinate information for the input sketches can be determined correctly.The input 2D sketches are thus lifted to provide 3D construction curves for subsequent free-form surface generation.

4.4 Generation of parametric surfaces

For each node Ii,the z-depth information of its sketch curves has been recovered and the 3D construction curves have been obtained.The next step is to generate a smooth surface to fit these construction curves for each node.To reconstruct 3D free-form objects,Severn et al.[36]generated a parametric blending surface by sweeping a variable sized circle along a medial axis of two planar sketches.Here,given four 3D construction curves, our cross-sectional surface blending scheme sweeps a ring of two semi-ellipses in such a way that the final parametric surface passes through these construction curves(see Fig.6(a)).As noted in Section 3.1,each of the four construction curves are sampled using the same number of points,and corresponding sets of four points sampled on different curves are used to generate a closed planar sweeping curve.However, the selected sets of four points are not in general located on a single plane.To overcome this issue, our improved cross-sectional blending scheme first determines a plane passing through the center of the line segment connecting two symmetric points.Its normal is determined by the cross product of the two directions connecting the general points and the symmetric points respectively.Then,the two general points are updated to be the intersection points of this plane with the two general curves.As a result, the four points are now located in the same plane and can be interpolated by two parameterized semiellipses(see Fig.6(a))as follows.

Overall,the reconstructed parametric surface S(u,v) is created by translating tu(v)along the medial axis of Csi(u)andThe final shape component is the parametric blending surface S(u,v)=tu(v);it is discretized as a triangle mesh(see Fig.6(b)).

4.5 Building up complex symmetric freeform shapes

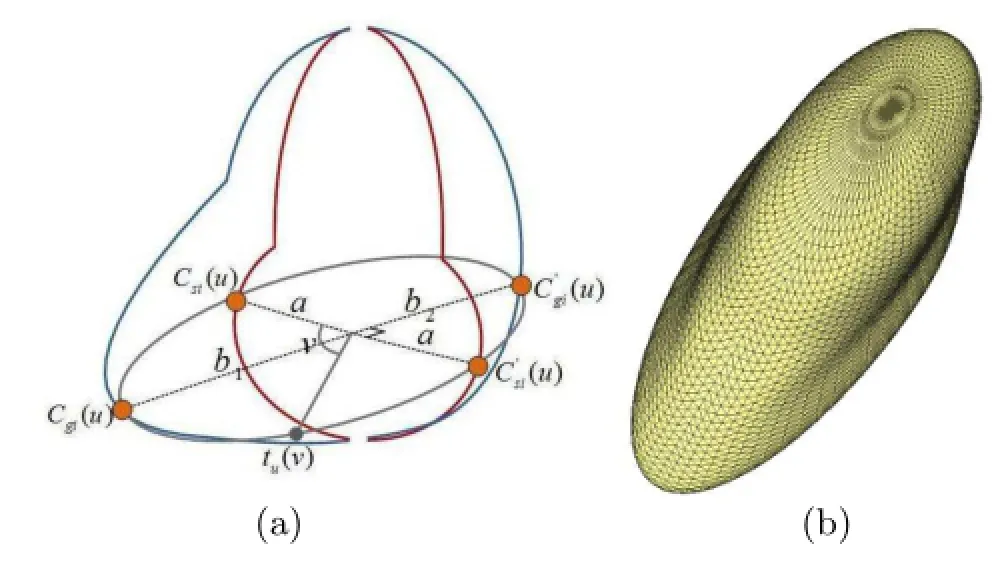
Fig.6 The parametric surface generated for one shape component.Four sample points determine a sweep contour made up of two semi-ellipses(a)that are smoothly connected at the symmetric points.(b)shows the final generated shape component.

To create complex symmetric free-form shapes,ourSymmSketch system separates the whole object into several components.Each shape component is created successively to build up the final shape.Once the user has finished the sketches for one component, our modeling system creates the corresponding 3D shape component interactively.This progressive modeling process provides the user with an intuitive design approach.The user can continue sketching after they have finished inputting the previous shape component.They can also remove some existing inaccurate sketches to allow them to be redrawn. The user can also add extra sketches to add further details to the object,increasing its complexity. Figure 7 illustrates an example of progressively creating a symmetric 3D free-form shape using our SymmSketch system.

5 Experimental results and discussion

All algorithms in this paper have been implemented in C++using OSG(Open Scene Graph)for graphics display,running on a 2.6 GHz Pentium(R)Dual-Core PC.From the user input 2D sketches,the main steps of our reconstruction approach include the computation of 3D construction curves for each shapecomponent,and thegenerationof smooth parametric surfaces using an improved crosssectional blending scheme.The experimental results show its effectiveness for building up various types of 3D free-form symmetric shapes.

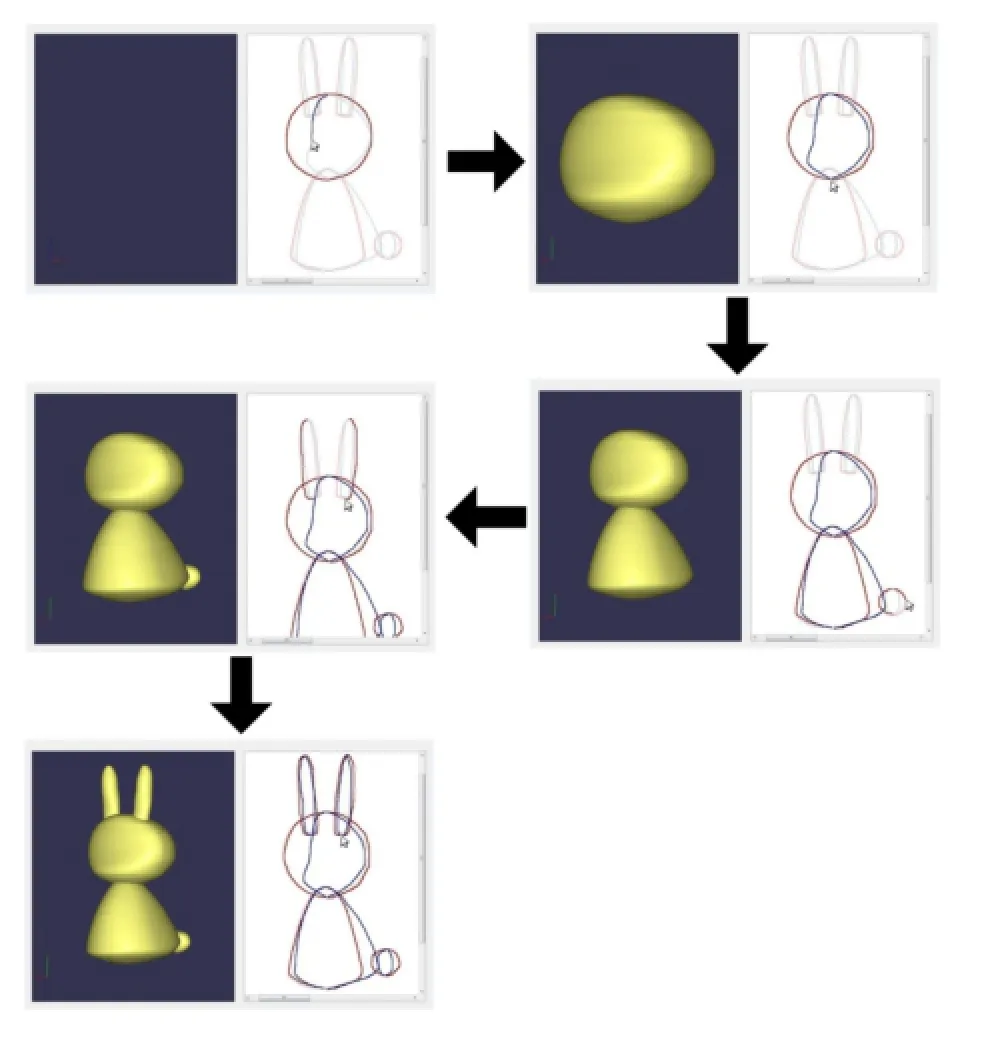
Fig.7 Creating complex symmetric 3D shapes in a progressive manner.

5.1 Creation ofsymmetric3D free-form shapes

Our SymmSketch system is suitable for various types of 3D free-form shapes,particularly mirrorsymmetric complex shapes comprising several components.Our modeling system has been tested by several novice student users which shows its effectiveness.After about 5min training in the use of 2D sketching approach,user can create common objects and simple cartoon characters interactively (see Fig.8). A user’s freehand sketch may not very accurately represent a real symmetric object. However,our reconstruction approach is insensitive to small human errors in the input drawings as our approach for recovering z-depth information for construction curves intrinsically maintains the property of mirror symmetry.

Alternatively,in order to accurately create 3D free-form shapes,user can include existing 2D line drawings to assist sketching tasks.Designers can simply depict the sketch lines on the sketching plane according to the provided line drawings.To create complex 3D free-form objects,our SymmSketch system can effectively control shape components to produce desired artistic effects,such as the body of a duck,the head of an ostrich or dog,and the plumage of a bird as shown in Fig.9.Here,column(a)in Fig.9 shows line drawings taken from real papers, column(b)gives the user drawn sketches based on these drawings,and columns(c)and(d)show the final generated 3D free-form objects from two different view directions.We can see that local sharp features can be generated by our modeling algorithm, such as the beak of the bird in the last row of Fig.9. However,we can also see that the reconstructed 3D shape may be a little thicker than the real object. This is because the construction curves may not be the silhouettes of the reconstructed objects.

5.2 Comparison with other 3D object reconstruction algorithms

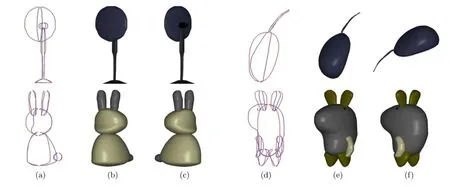
Fig.8 Creation of different free-form shapes from user sketches.The first figure of each group shows the user input 2D sketches (columns(a)and(d)),and other figures of each group show the final generated 3D free-form shapes from two different viewing directions(columns(b)and(c),and columns(e)and(f)).

Given single view 2D sketches,our reconstruction approach can generate complex free-form shapes effectively and conveniently. Our reconstruction approach relies only on the 2D sketch content itself, and thus avoids any fuzzy or complicated operations to assemble multiple shape components into a single object.Moreover,an important advantage of our SymmSketch system is that it can provide a good degree of freedom for effectively controlling the final reconstructed shapes by employing four construction curves.Unlike the most closely related approach presented by Cordier et al.[19],our 3D object reconstruction method can create complex free-form shapes with specific geometric features,such as the sharp jagged tail of a woman’s hair clasp,a flat wine bottle,and a peaked cap as shown in Fig.10.

5.3 Limitations of our algorithm

Oursymmetric free-form objectreconstruction approach always creates each shape component from four construction curves,whether it is a selfsymmetric shape component or a shape component symmetrically related to another one.One limitation of our approach is that to correctly recognize and reconstruct complex 3D shapes,the input sketches should be drawn on a sketching plane in a specific order to allow inference of the free-form shape(see Fig.4).Furthermore,our modeling system allows only a single symmetry plane for creating the whole shape.Of course,it could generate more general free-form objects if multiple symmetry planes were allowed.However,such a scheme would make the user input task more difficult to permit handling several symmetry planes on one sketching plane,and would need some new user interactions for sketching different shape components.

Another limitation of our modeling method is that some fork-like shapes can be difficult to recover correctly.For example,Fig.11 shows an unexpected reconstruction result of a funnel like shape using our method for a fork-like structure-the whole symmetric object is recovered as a single component. In future,some flexible mechanism for generating such shapes should be investigated.

6 Conclusions and future work

This paper has presented SymmSketch,a system for creatingsymmetric3D free-form shapeswhich consist of two types of shape components, self-symmetric componentsand onesthatare symmetrically related to another component with respect to a symmetry plane.The user needs draw only a few strokes,after which our reconstruction method can automatically infer the relative depth of different shape components due to the presence of mirror symmetry.Our experimental results illustrate the effectiveness of our system for generating various types of free-form symmetric shapes.

Our future work will consider the following issues. The current system prevents the user from drawing the sketches in an arbitrary order.An algorithm for matching the symmetric curves automatically would help to overcome this issue.Our modeling system can only reconstruct free-form shapes with symmetry with respect to a unique symmetry plane.We hope to develop a 3D modeling system for generating complex shapes which may includeseveral local mirror symmetries with respect to different symmetry planes.

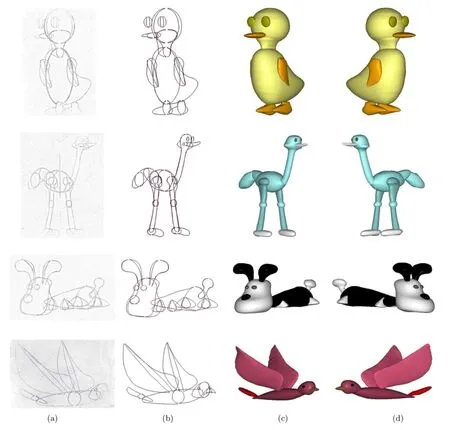
Fig.9 Free-form shapes reconstructed by redrawing existing line drawings.(a)Line drawings;(b)user sketches which recreate these drawings;(c)and(d)the final generated symmetric 3D free-form shapes,shown in two different views.

Fig.10 Comparison of free-form shapes reconstructed by different methods.(a)The user input sketch containing the symmetric curves and the general curves;(b)reconstructed 3D shapes using only two symmetric curves as in Cordier et al.’s method;and(c) 3D shapes reconstructed using our approach.

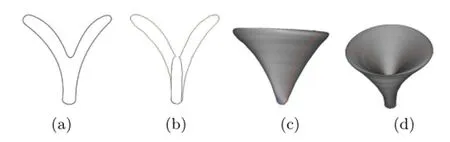
Fig.11 An unexpected reconstruction:the intent was to create a forked structure(a),but the result was a funnel-like shape(c) and(d).

Acknowledgements

This research work is supported by the National Natural Science Foundation of China under Grant Nos.61272309 and 61303138.The 3D models are courtesy of the Aim@Shape,Stanford University and Princeton University.

Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use,distribution,and reproduction in any medium,provided the original author(s)and the source are credited.

[1]Blair,P.Advanced Animation.Walter T.Foster Publisher,1949.

[2]Olsen,L.;Samavati,F.F.;Sousa,M.C.;Jorge,J. A.Sketch-based modeling:A survey.Computers& Graphics Vol.33,No.1,85-103,2009.

[3]Gingold,Y.;Igarashi,T.;Zorin,D.Structured annotations for 2D-to-3D modeling. ACM Transactions on Graphics Vol.28,No.5,Article No. 148,2009.

[4]Shtof,A.;Agathos,A.;Gingold,Y.;Shamir,A.; Cohen-Or,D.Geosemantic snapping for sketch-based modeling.Computer Graphics Forum Vol.32,No.2, 245-253,2013.

[5]Company,P.;Piquer,A.;Contero,M.;Naya,F. A survey on geometrical reconstruction as a core technology to sketch-based modeling.Computers& Graphics Vol.29,No.6,892-904,2005.

[6]Zeleznik,R.C.;Herndon,K.P.;Hughes,J.F. SKETCH:An interface for sketching 3D scenes. In: Proceedings of the 23rd annual conference on Computer graphics and interactive techniques,163-170,1996.

[7]Igarashi,T.;Matsuoka,S.;Tanaka,H.Teddy: A sketching interface for 3D freeform design.In: Proceedings ofthe 26th annualconference on Computer graphics and interactive techniques,409-416,1999.

[8]Schmidt,R.;Wyvill,B.;Sousa,M.C.;Jorge, J.A.ShapeShop: Sketchbased solid modeling with BlobTrees.In: Proceedings ofthe 2nd EUROGRAPHICS Workshop on Sketch-Based Interfaces and Modeling,53-62,2005.

[9]Karpenko,O.A.;Hughes,J.F.SmoothSketch: 3D free-form shapes from complex sketches.ACM Transactions on Graphics Vol.25,No.3,589-598, 2006.

[10]Nealen,A.;Igarashi,T.;Sorkin,O.;Alexa,M. FiberMesh: Designing freeform surfaces with 3D curves.ACM Transactions on Graphics Vol.26,No. 3,Article No.41,2007.

[11]Bae,S.-H.;Balakrishnan,R.;Singh,K.ILoveSketch: As-natural-as-possible sketching system for creating 3d curve models.In:Proceedings of the 21st annual ACM symposium on User interface software and technology,151-160,2008.

[12]Boros´an,P.;Jin,M.;DeCarlo,D.;Gingold,Y.; Nealen,A.RigMesh:Automatic rigging for part-based shape modeling and deformation.ACM Transactions on Graphics Vol.31,No.6,Article No.198,2012.

[13]Xu,K.;Chen,K.;Fu,H.;Sun,W.-L.;Hu, S.-M.Sketch2Scene: Sketch-based co-retrieval and co-placement of 3D models.ACM Transactions on Graphics Vol.32,No.4,Article No.123,2013.

[14]Levi,Z.; Gotsman,C.ArtiSketch: A system for articulated sketch modeling.Computer Graphics Forum Vol.32,No.2,235-244,2013.

[15]Bae,S.-H.;Kijima,R.;Kim,W.-S.Digital styling for designers:3D plane-symmetric freeform curve creation using sketch interface.Lecture Notes in Computer Science Vol.2669,701-710,2003.

[16]Piquer,A.;Martin,R.;Company,P.Skewed mirror symmetry for depth estimation in 3d line-drawings. Lecture Notes in Computer Science Vol.3088,142-153,2004.

[17]Chen,X.;Kang,S.B.;Xu,Y.-Q.;Dorsey,J.;Shum, H.-Y.Sketching reality:Realistic interpretation of architectural designs.ACM Transactions on Graphics Vol.27,No.2,Article No.11,2008.

[18]Cheon,S.-U.;Han,S.A template-based reconstruction of plane-symmetric 3D models from freehand sketches. Computer-Aided Design Vol.40,No.9,975-986,2008. [19]Cordier,F.;Seo,H.;Park,J.;Noh,J.Sketching of mirror-symmetric shapes.IEEE Transactions on Visualization and Computer Graphics Vol.17,No.11, 1650-1662,2011.

[20]Andre, A.; Saito, S.Single-view sketch based modeling.In:Proceedings of the Eighth Eurographics Symposium on Sketch-Based Interfaces and Modeling, 133-140,2011.

[21]Mitani,J.;Suzuki,H.;Kimura,F.3D sketch:Sketchbased model reconstruction and rendering.In:From Geometric Modeling to Shape Modeling.Cuguni,U.; Wozny,M.Eds.Norwell,MA,USA:Kluwer Academic Publishers,85-98,2002.

[22]Varley,P.A.C.;Takahashi,Y.;Mitani,J.;Suzuki,H. A two-stage approach for interpreting line drawings ofcurved objects.In:ProceedingsoftheFirst Eurographics conference on Sketch-Based Interfaces and Modeling,117-126,2004.

[23]Nealen,A.;Sorkine,O.;Alexa,M.;Cohen-Or,D. A sketch-based interface for detail-preserving mesh editing.ACM Transactions on Graphics Vol.24,No. 3,1142-1147,2005.

[24]Masry,M.;Lipson,H.A sketch-based interface for iterative design and analysis of 3D objects.In:ACM SIGGRAPH 2007 courses,Article No.31,2007.

[25]Li,Y.;Pizlo,Z.;Steinman,R.M.A computational model that recovers the 3D shape of an object from a single 2D retinal representation.Vision Research Vol. 49,No.9,979-991,2009.

[26]Funkhouser,T.;Min,P.;Kazhdan,M.;Chen,J.; Halderman,A.;Dobkin,D.;Jacobs,D.A search engine for 3D models.ACM Transactions on Graphics Vol.22,No.1,83-105,2003.

[27]Shin,H.;Igarashi,T.Magic canvas:Interactive design of a 3-D scene prototype from freehand sketches.In: Proceedings of Graphics Interface,63-70,2007.

[28]Lee,J.;Funkhouser,T.Sketch-based search and composition of 3D models.In:Proceedings of the Fifth Eurographics conference on Sketch-Based Interfaces and Modeling,97-104,2008.

[29]Li,Z.;Liu,J.;Tang,X.A closed-form solution to 3D reconstruction of piecewise planar objects from single images.In:IEEE Conference on Computer Vision and Pattern Recognition,1-6,2007.

[30]Wang,Y.;Chen,Y.;Liu,J.;Tang,X.3D reconstruction of curved objects from single 2D line drawings.In:IEEE Conference on Computer Vision and Pattern Recognition,1834-1841,2009.

[31]Xue,T.;Liu,J.;Tang,X.3-D modeling from a single view of a symmetric object.IEEE Transactions on Image Processing Vol.21,No.9,4180-4189,2012.

[32]Chen,T.;Zhu,Z.;Shamir,A.;Hu,S.-M.;Cohen-Or, D.3-sweep:Extracting editable objects from a single photo.ACM Transactions on Graphics Vol.32,No.6, Article No.195,2013.

[33]¨Oztireli,A.C.;Uyumaz,U.;Popa,T.;Sheffer,A.; Gross,M.3D modeling with a symmetric sketch.In: Proceedings of the Eighth Eurographics Symposium on Sketch-Based Interfaces and Modeling,23-30,2011.

[34]Cordier,F.;Seo,H.;Melkemi,M.;Sapidis,N.S. Inferring mirror symmetric 3D shapes from sketches. Computer-Aided Design Vol.45,No.2,301-311,2013.

[35]Farin,G.Curves and Surfaces for CAGD:A Practical Guide,5th edn.San Francisco,CA,USA:Morgan Kaufmann Publishers Inc.,2002.

[36]Severn,A.;Samavati,F.F.;Cherlin,J.J.;Sousa,M. S.;Jorge,J.A.Sketch-based modeling and assembling with few strokes.In: Sketch-Based Interfaces and Modeling.Jorge,J.;Samavati,F.Eds.London,UK: Springer,255-286,2011.

YongweiMiaoreceivedhisPh.D. degree in computer graphics from theStateKey Lab.ofCAD & CG at Zhejiang University in March 2007.From February 2008 to February 2009,he worked as a visiting scholar in the University of Z¨urich,Switzerland. From November 2011 to May 2012,he worked as a visiting scholar in the University of Maryland, USA.Dr.Miao is a professor in the College of Computer Science and Technology,Zhejiang University of Technology, China.His research interests include computer graphics, digital geometry processing,visual media computing,3D reconstruction,and computer vision.

Feixia Hu is a master’s degree candidate in the College of Computer Science and Technology, Zhejiang University of Technology,China. His research interests include computer graphics,visual media computing,and 3D reconstruction.

Xudong Zhang is a faculty member of the College of Computer Science and Technology,Zhejiang University of Technology,China. His research interestsinclude computer graphics, visual media computing,and computer vision.

Jiazhou Chen is a lecturer in the College of Computer Science and Technology, Zhejiang University of Technology,China. Before that,he wasajointPh.D.studentbetween Bordeaux University(INRIA Bordeaux Sud-Ouest), France and Zhejiang University (the State Key Lab.of CAD&CG at Zhejiang University),China.He obtained the French doctoral diploma from Bordeaux University in July 2012,and also obtained the Chinese doctoral diploma from Zhejiang University in December 2012.His research interests include computer graphics,image and video stylization,augmented reality,and visual media computing.

Renato Pajarola received a Dr.Sc. Techn. in computer science in 1998 from the Swiss Federal Institute of Technology (ETH)Z¨urich.Aftera postdoc in the Graphics,Visualization &Usability Center at Georgia Tech., he joined the University of California Irvine in 1999 as an assistant professor where he founded the Computer Graphics Lab.He is a now full professor in the Department of Informatics,

University of Z¨urich,Switzerland.His research interests include real-time 3D graphics,scientific visualization,and interactive 3D multimedia.

1College of Computer Science and Technology, Zhejiang University of Technology,Hangzhou 310023, China.E-mail:ywmiao@zjut.edu.cn(),yongweimiao@ gmail.com().

2Department ofInformatics, University of Zu¨rich, Zu¨rich CH-8050,Switzerland.E-mail:pajarola@ifi.uzh. ch.

Manuscript received:2014-09-12;accepted:2015-01-05