音乐信号小波阈值去噪模型及其应用

郑勋烨，陈保毕

（中国地质大学（北京）数理学院，北京100083）

小波去噪的方法很多，如小波变换模极大值法、非线性小波阈值法、平移不变量法、屏蔽相关法以及多小波法等。阈值去噪法是最常用的一种小波去噪法。

1 小波阈值去噪方法

小波阈值滤波去噪方法的原理是信号经小波变换后，其能量集中于少数小波系数［1］，由此可对变换系数进行截断阈值，去除噪声。

含噪信号［2］形如：

式中，s i（）为含噪信号；x i（）为原始信号；z i（）是高斯白噪声。

从含噪信号s（i）中重建原始信号x（i），可依如下步骤［3～5］进行：①选择合适的小波基和小波分解层数，将含噪信号作小波分解至层，得到相应的小波分解系数。②对小波系数作阈值，得到原始信号小波系数估值。③作小波逆变换，将阈值后的小波系数重构，得到原始信号。

去噪过程中的关键点如下：①选择合适的小波基及小波分解层数；②选择合适的小阈值和阈值函数。

2 选择小波基和小波分解层数

确定合适的小波基和小波分解层数的解决方案如下：①依据小波优越性判别标准，选择具有较短紧支撑的正交小波基，拥有高阶消失矩，对称性良好，且具有一定的光滑性。②选定小波分解层数J，将含噪信号分解至J层，得到相应的系数。③改变小波分解层数J，重新进行分解并比较去噪结果，直至获得最合适的小波分解层数。在去噪的过程中，信号的分解层数不宜太大，一般取4～5层即可。

3 选择阈值和阈值函数

3.1 选择阈值函数

常用的阈值函数包括硬阈值函数、软阈值函数和几乎硬阈值函数［6，7］。

硬阈值函数形如：

式中，t为阈值；γ为小波系数。

软阈值函数形如：

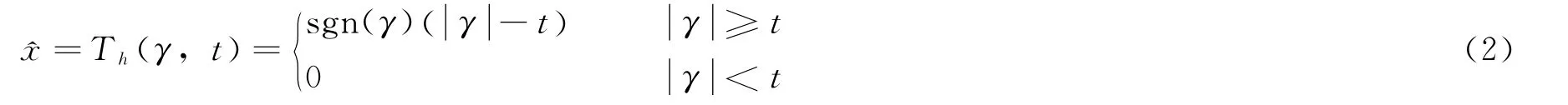
另外，还有一种几乎硬阈值函数，其定义为：

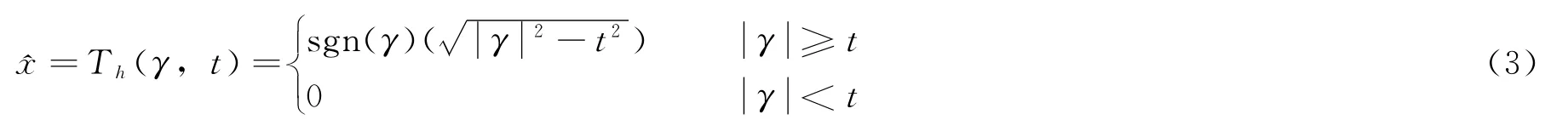
鉴于软阈值处理方法在某些方面优于硬阈值处理方法，笔者采用软阈值函数。

3.2 选择阈值t

通常可依据sqtwolog规则、rigrsure规则、minimaxi规则和heursure规则［8，9］来选取阈值t。 以下均设含噪信号x（t）在尺度1～j（1＜j＜J）上的小波系数总个数和为n，J为二进尺度，噪声均方差为σ。

1）通用阈值t1（sqtwolog规则）。通用阈值定义为：

2）Stein无偏风险阈值t2（rigrure规则）。基于无偏似然估计原理，计算给定阈值t的极大似然估计，再将t最小化，即得Stein无偏风险阈值。

设向量W 的元素是从小到大顺序排列的小波系数的平方，即W＝（w1，w2，…，wn）且w1＜w2＜…＜wn，设风险向量R的元素为：

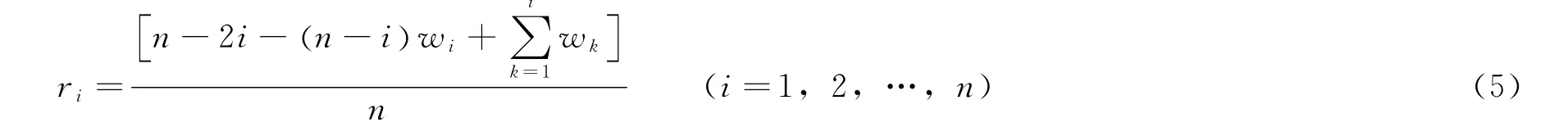
以最小元素值rb为风险值，由rb的下标b确定对应的wb，则Stein无偏风险阈值为：

3）试探法的无偏风险阈值t3（heursure规则）。设n个小波系数平方和为s，令：

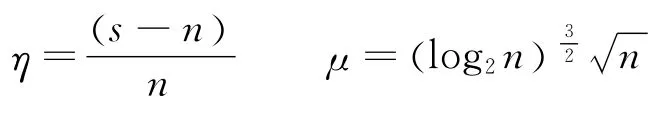
则试探法的无偏风险阈值定义为：

4）极小极大准则阈值t4（minimaxi规则）。这是一种实现原始信号与去噪信号的最大均方误差最小化的固定阈值，定义为：

式中，W1，k表示尺度为1的小波系数。

选择好合适的小波基、小波分解层数以及合适的小波阈值和阈值函数，就可以对含噪信号进行小波滤波处理。

4 小波去噪性能的评价原则

评价去噪结果的原则主要有：①光滑性。去噪后信号与原信号至少同等光滑。②相似性。去噪后信号与原信号的误差实现最小化。实践中，分别用去噪信号与原始信号的标准差，以及去噪信号与原始信号的能量比来体现这2个原则。

此外，最关注的是去噪后的效果。对此，笔者通过信噪比来衡量。其定义如下：

式中，x（n）为处理前的音乐信号；x（n）为处理后的音乐信号。

5 小波阈值滤波音乐去噪模型及结果分析

笔者选择不同类型的小波做仿真试验，分别采用全局阈值和分层阈值去噪法，来观察不同的小波选择对去噪结果的影响。同时，选择某种固定的小波，比较这2种去噪方法的优劣。下面，笔者通过歌曲《butterfly》中的一段音乐信号进行去噪来对上述问题进行阐述。所添加的噪声为随机噪声。

5.1 小波全局阈值去噪模型及结果分析

编写程序，利用db4、sym8、coif5小波，分解层数为4层［10］。试验结果如表1、图1～3所示。

由表1、图1～3可以看出，不论采用何种小波，全局阈值去噪法都能使信号的能量得到最大限度的保留；不同的小波对信号的能量比影响并不大，只是对信号的信噪比影响较显著。db4小波所得的信噪比略高，这说明在信号去噪过程中小波的选择对去噪结果有重要影响。

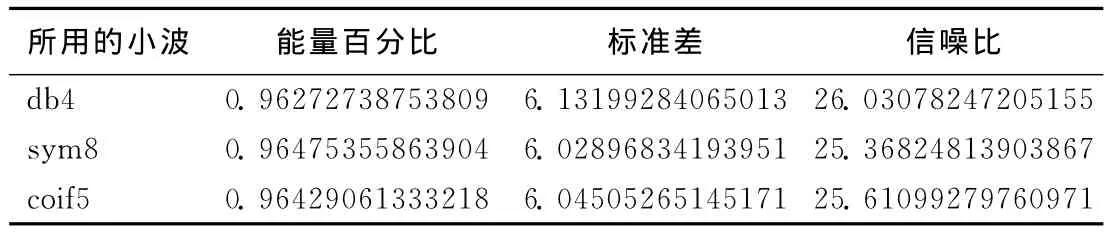
表1 全局阈值去噪的结果

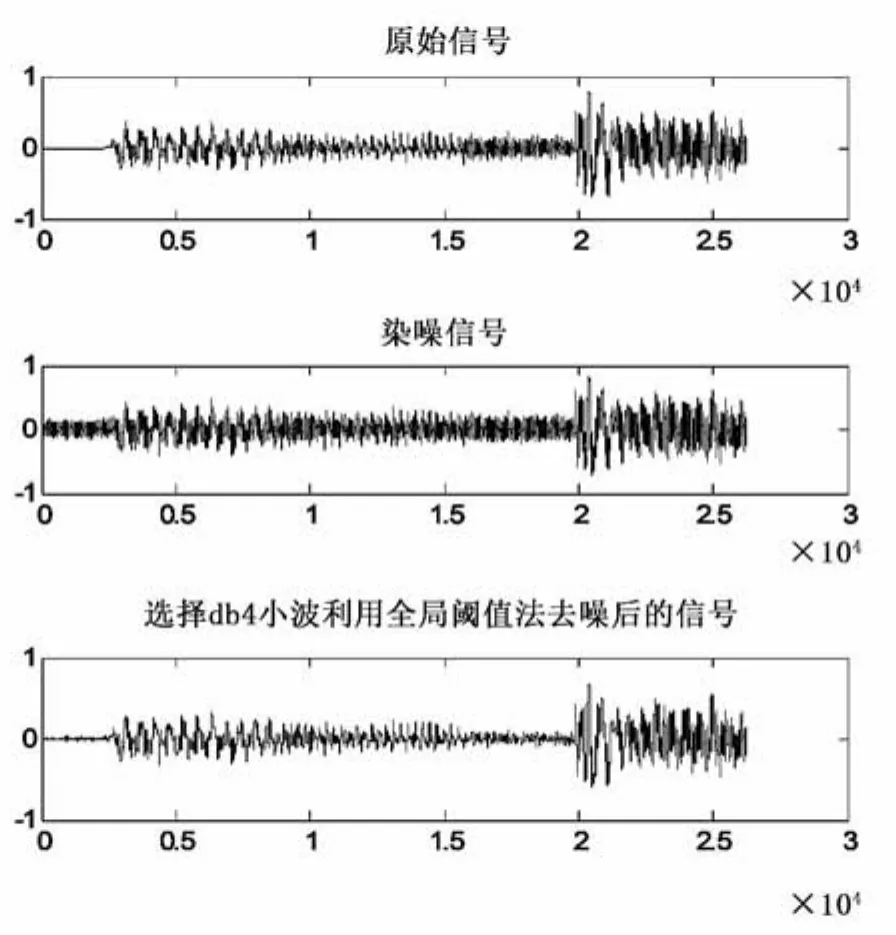
图1 全局阈值去噪的db4小波分解结果示意图

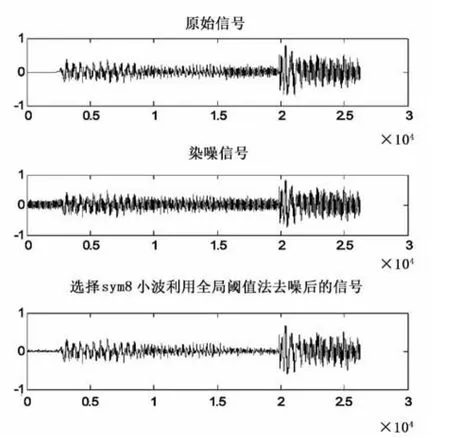
图2 全局阈值去噪的sym8小波分解结果示意图

5.2 小波分层阈值去噪模型及结果分析

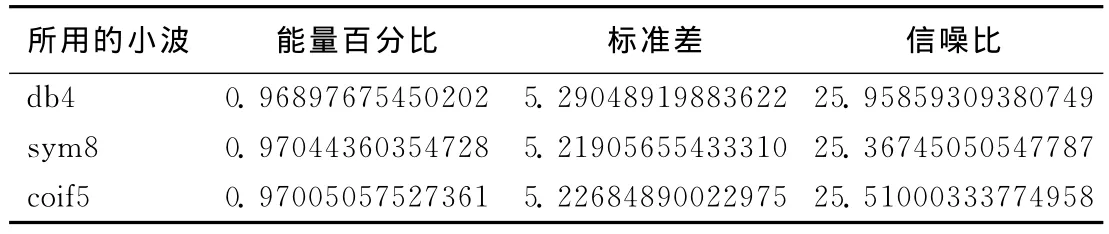
表2 分层阈值去噪的结果

全局阈值并没有充分应用每一层所分解的小波系数。因此，作为对全局阈值去噪法的一种改进，笔者利用分层阈值对小波系数处理。试验中，所采用的小波是db4、sym8、coif5，分解层数为4层。所得结果如表2和图4～6所示。

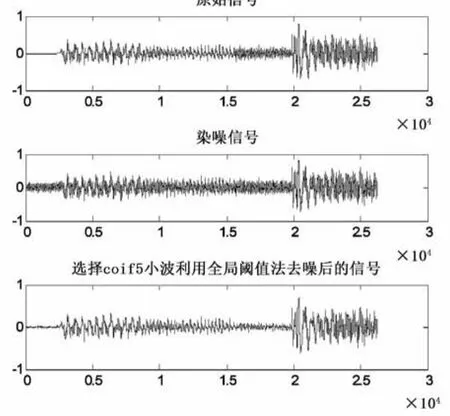
图3 全局阈值去噪的coif5小波分解结果示意图

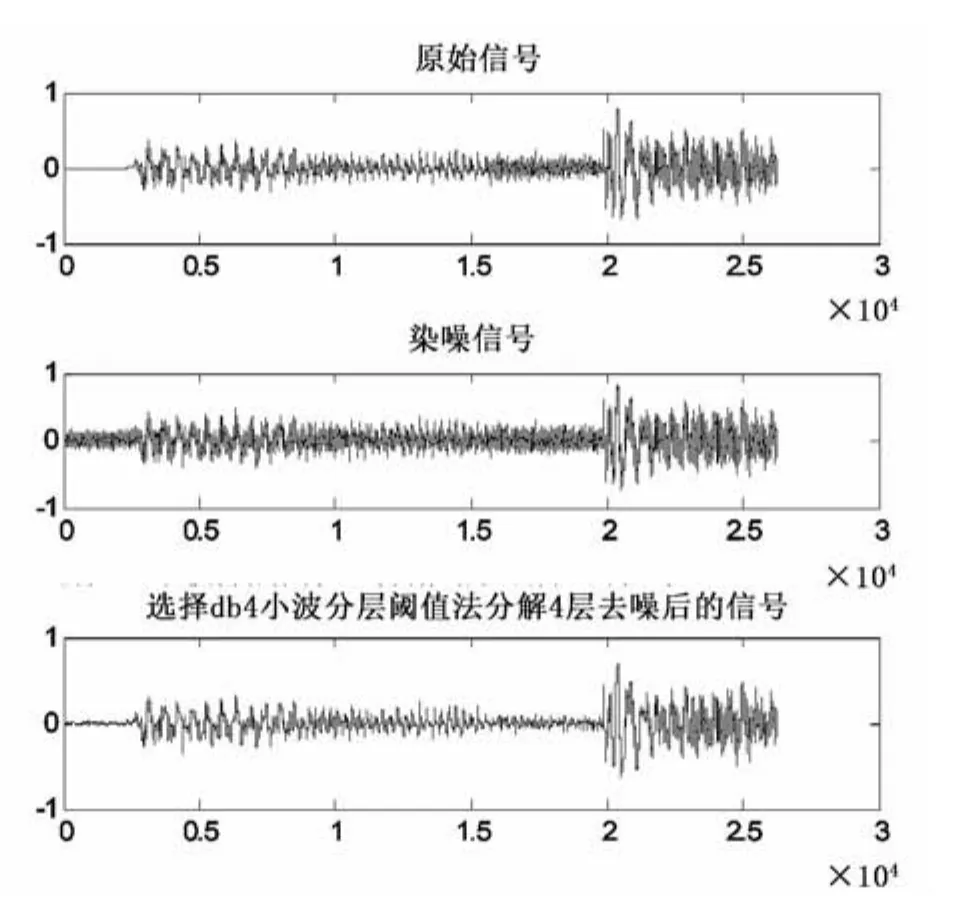
图4 分层阈值去噪的db4小波分解结果示意图

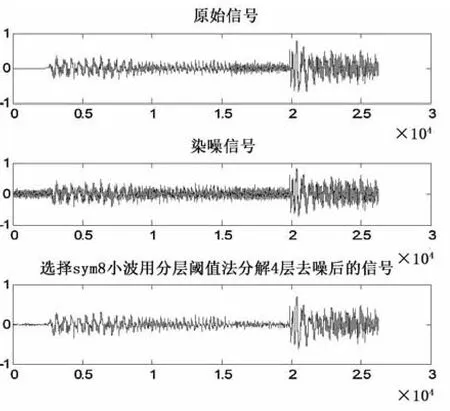
图5 分层阈值去噪的sym8小波分解结果示意图

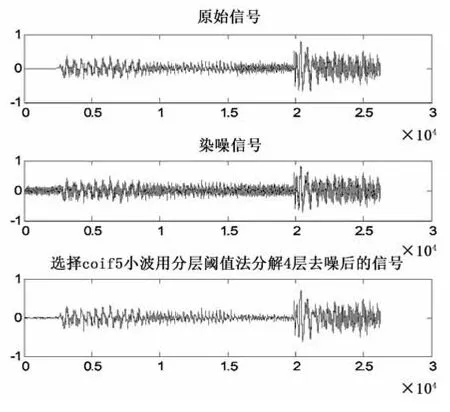
图6 分层阈值去噪的coif5小波分解结果示意图

从表2和图4～6可以看出：相对于全局阈值去噪法，信号的能量比有所提升，这主要是阈值对每一层的小波分解系数都进行作用，滤去了更多的噪声信息能量；和全局阈值去噪法相同，不同的小波对信号能量比和信噪比影响并不大；和全局阈值去噪法相比，标准偏差减小，信号的整体光滑性得到增强。

5.3 不同分解层数对去噪结果的影响

利用db4小波，对含噪音乐信号分别作分层阈值法的3、4、5、6、7层分解。所得数据与结果如表3和图7～11所示。

通过上述试验结果可以得出如下结论：①随着分解层数的增加，音乐信号的能量百分比呈下降趋势。主要原因在于：由于分解层数的增加，每一层的分解系数都被阈值所作用。这样，被滤去的信号的有效成分就越多，从而使得信号能量百分比降低。②随着分解层数的增加，信号的标准差越来越大。这说明信号的分解层数越多，信号的局部光滑性得到了增强，然而信号的整体相似性却降低了。③随着分解层数的增加，信噪比先增加，后下降。这说明刚开始随着信号分解层数的增加，噪声得到了有效去除。然而，随着分解层数进一步地增加（比如分解到8层时），信号的某些有效成分被作为噪声错误地去除了，从而使得信噪比降低。因此，在去噪的过程中，信号的分解层数不宜太大，一般取4～5层即可。

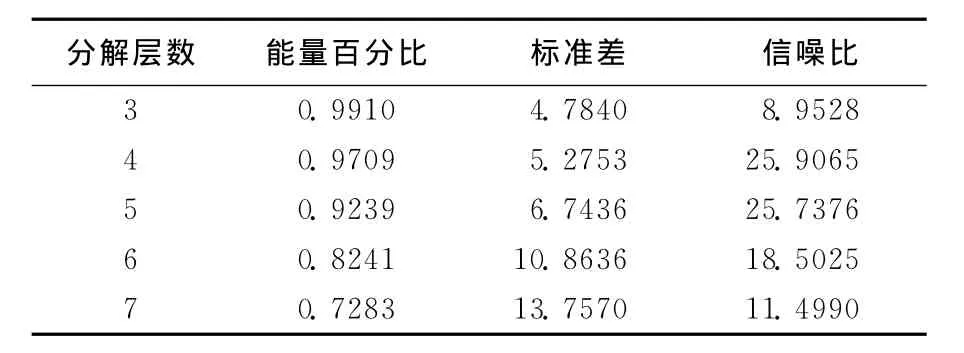
表3 不同分解层数对去噪效果的影响的模拟结果

6 结语

虽然小波阈值去噪方法简单易用，但和语音信号不同，在音乐信号中，还掺杂着乐器演奏所发出的声音。因此，在现有的噪声估计模型中，很有可能把音乐当作噪声来进行处理，使得重构系数变小。由此可以看出，今后对于音乐去噪的研究，应该建立一种和语音信号不同的阈值估计模型来加强乐音和噪声之间的识别，这样才能使音乐去噪的效果更好。

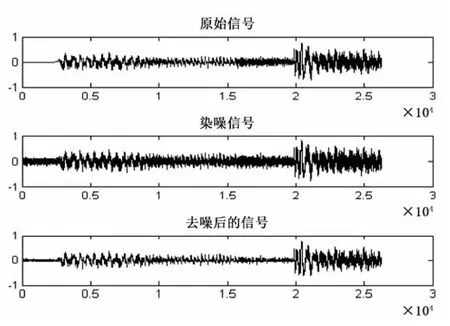
图7 分解层数为3时去噪效果图

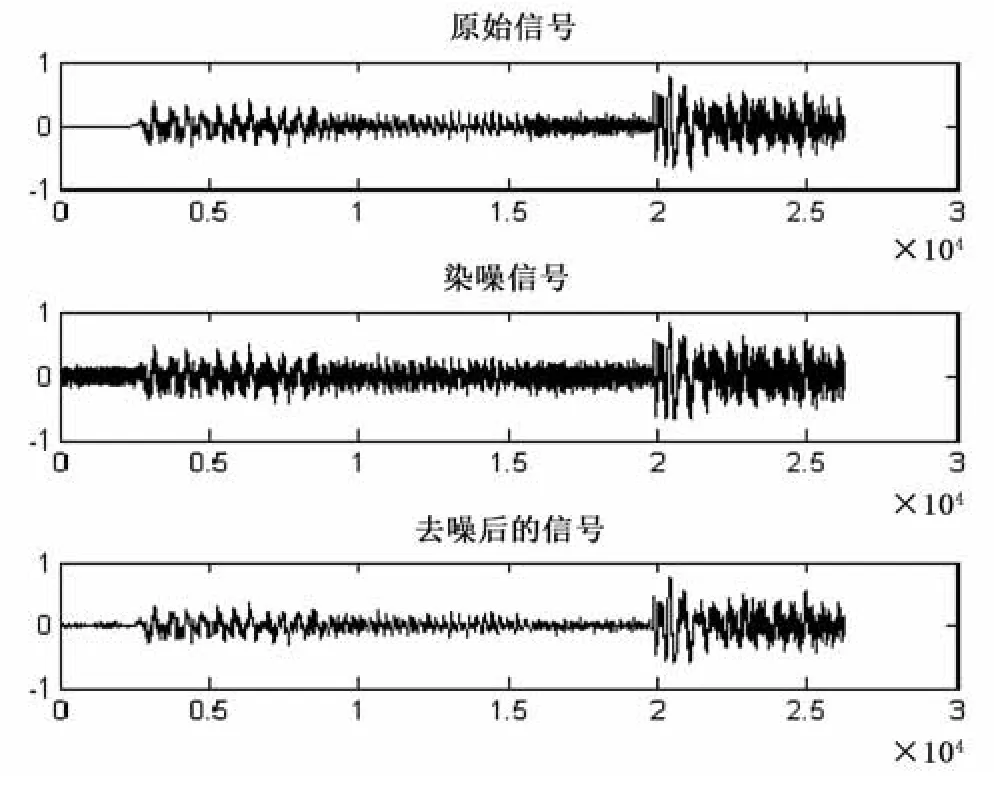
图8 分解层数为4时去噪效果图

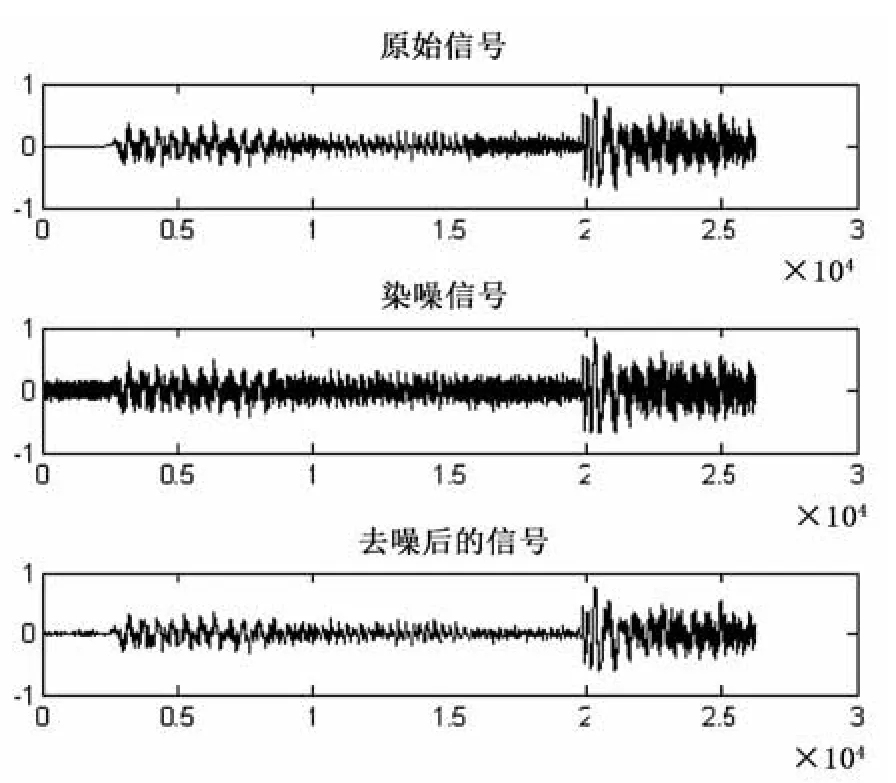
图9 分解层数为5时去噪效果图

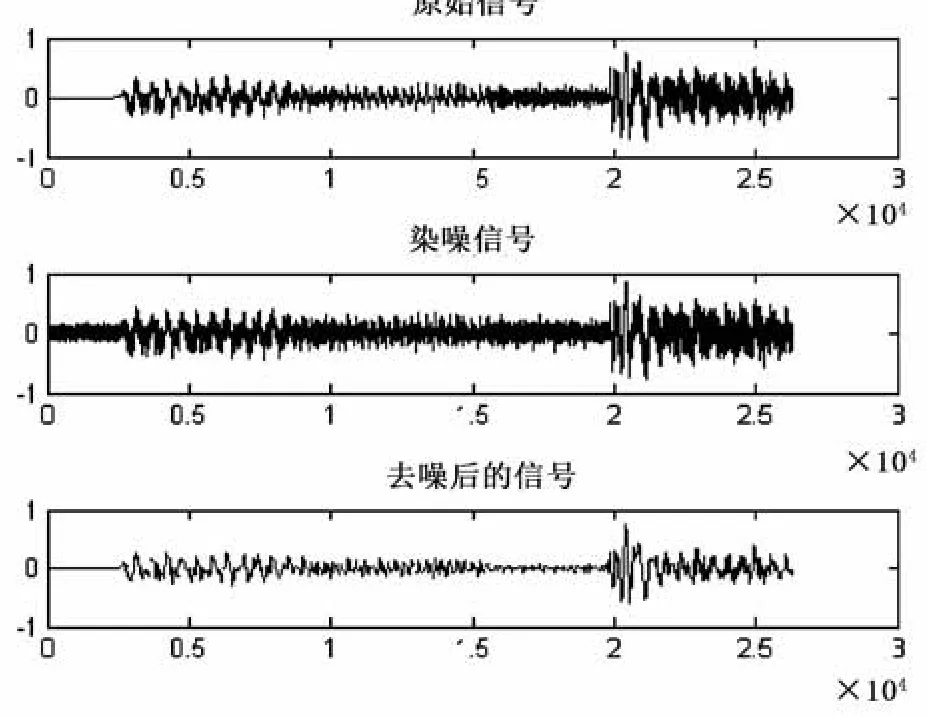
图10 分解层数为6时去噪效果图

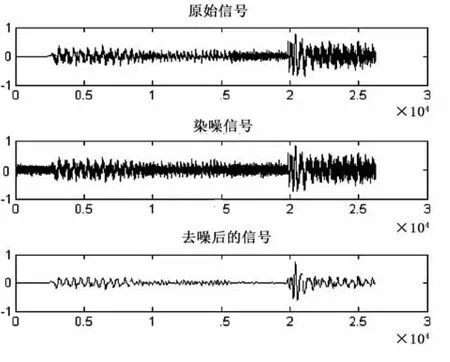
图11 分解层数为7时去噪效果图

［1］程正兴.小波分析算法与应用 ［M］.西安：西安交通大学出版社，1998.

［2］郑治真，沈萍，杨选辉，等.小波变换及其Matlab工具的应用 ［M］.北京：地震出版社，2000.

［3］盛英.基于小波变换的语音信号降噪研究 ［D］.哈尔滨：哈尔滨工程大学，2007.

［4］高智芳，张家新.基于小波变换的除噪方法及其应用研究 ［J］.信息安全与通信保密，2007（6）：102～104.

［5］李建平，张万萍，陈廷槐，等.从傅里叶分析到小波分析：回顾与发展 ［J］.计算机科学，1999（12）：29～30.

［6］刘娟花.小波分析在语音去噪中的应用 ［D］.西安：西安理工大学，2004.

［7］李建平.小波分析与信号处理 ［M］.重庆：重庆出版社，1997.

［8］高成，余啸海，李阳明，等.Matlab小波分析与应用 ［M］.第2版.北京：国防工业出版社，2007.

［9］许山川.基于小波变换的语音信号去噪研究 ［D］.秦皇岛：燕山大学，2006.

［10］王沫然.Matlab与科学计算 ［M］.第2版.北京：电子工业出版社，2004：126～185.