基于ANSYS 的金属声场仿真及缺陷识别方法研究*

高 捷，陈友兴，王召巴

(中北大学信息与通信工程学院，山西 太原 030051)

众所周知，在国防军工、航空航天、交通运输等领域，金属柱状物体的应用一直很广泛，例如兵器中的弹体、汽车的零部件等。然而，在这些柱状物体的生产过程中，往往由于温度的瞬时变化、介质与模具的摩擦等原因，造成物体内部或表面产生不同程度的缺陷，这些缺陷常常会降低产品的使用效果，或在使用过程中受到各种外在因素的影响而产生结构缺陷损伤程度积累问题，引起重大的安全隐患。因而，在生产过程以及使用过程中，对产品进行无损检测具有十分重大的意义。

超声检测是目前应用最广的一种缺陷检测技术，由于超声波的穿透能力强、灵敏度高，且对人体无害，已被广泛应用于工业及高技术产业中。超声波的特点是传播能量大、方向性好，而且在介质内传播过程中遇到缺陷时会产生界面反射或者引起声速和能量衰减的变化，利用这一特性就可以达到检测缺陷的目的［1］。

超声波传播理论复杂，传播过程抽象，况且随着工业技术的不断发展，定性检测已不能满足实践的要求，需要定量地确定缺陷的几何特征(形状、尺寸和取向)和材料性能，这使得超声波检测人员对于仪器显示的波形数据正确解释需要丰富的经验，导致检测结果会有一定的主观性。在平时的检测中，就需要制作大量的对比试件进行模拟检测，分析波形，用实际检测波形与之对比，由此来提供检测结果评判的准确率。但是试件制作费时费力，而且试件的存储也比较麻烦。为了研究超声波传播理论，更好地利用超声波进行检测，并且避免以上问题，通过引入有限元分析软件直观的反应波的传播过程和声场特性，为缺陷评判提供理论数据和模型参考，提高缺陷检测的准确性。

本文同时采用有限元和实验两种手段对均匀介质中的缺陷检测进行研究。

1 超声检测方法

主要研究的对象为圆柱体，如图1 所示检测示意图。当检测无缺陷圆柱体时，如图1(a)所示，从探头发射出的超声脉冲波可以直接到达试件的底部，不会发生反射、折射现象。当检测有缺陷圆柱体时，超声波当没有遇到缺陷时，是以常速度沿着固定的路线不受干扰地向前传播的，但当遇到缺陷时，波与它的原来路径发生了偏离，产生折射、反射现象，因此，可以从中提取出缺陷特征回波信号，如图1(b)所示。

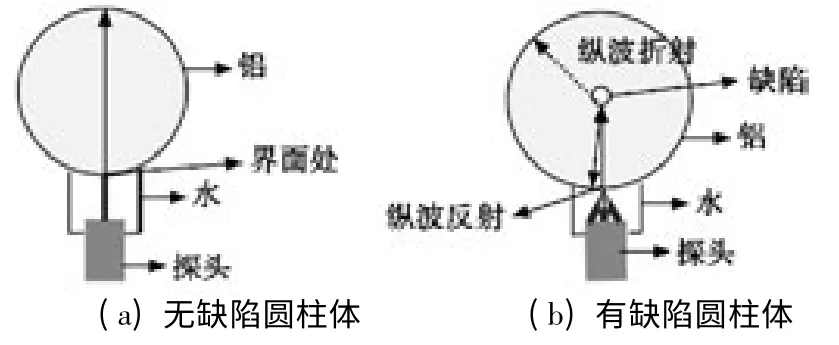
图1 圆柱体水浸检测示意图

2 研究对象以及实验对象

实验选用两个高为200 mm、底面半径为50 mm 的铝合金圆柱体试件作为研究对象，其中一个在构件底面的中心位置含有半径为5 mm 的圆柱形空穴缺陷，如图2(a)所示;另一个在底面的中心有一条光滑的长为100 mm，宽5 mm 的凹槽，如图2(b)所示。

图2 实验试件

使用图1 所示的超声检测方法，利用图2(c)所示的实验系统对图2(a)(b)的两个试件分别进行了超声信号采集，得到了两个试件的时域波形，从时域波形中读出始波与缺陷回波的时间差，依据公式2l=t ×v(l 为超声波传播的距离，t为探头接收到反射回波的时间，v 为超声波传播的速度)计算得到构件下表面与缺陷之间的距离，就可以得出缺陷的位置。对两个试件缺陷回波信号进行傅里叶变换，得到其频域变化情况。其中，圆形缺陷、槽形缺陷的时域波形和其频域变化情况如图3 所示。

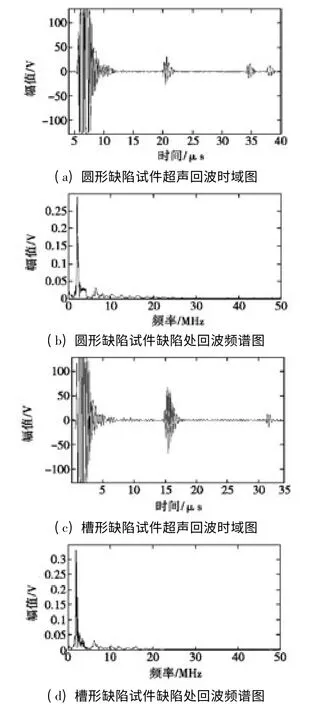
图3 实验试件超声回波时域图、频谱图

3 有限元模拟仿真结果

被检工件为铝，密度为2 700 kg/m3，弹性模量为70 GPa，泊松比为0.33，截面半径为50 mm，圆孔缺陷半径为5 mm，缺陷的截面模型如图4(a)所示。为获取比较细腻的波的传播图像，需对模型划分很细的网格。在波的传播计算中，单元在每个步长计算时沿波传播方向的长度应小于波长。根据参考文献［8］，选取单元尺寸小于激励频率下最短波长的十分之一。如果单元尺寸大于波长的十分之一，误差将迅速增大。但如果单元尺寸选得太小，对于同样面积的模型，单元数量将以尺寸缩小程度2 次幂的速度增长，且时间步长更小，因此计算的成本将迅速增大。同时，当单元尺寸小到一定程度时，舍入误差将随之增加。因而，在选取单元尺寸时，并非越小越好。所以，本文设置的单元尺寸是0.1 mm。

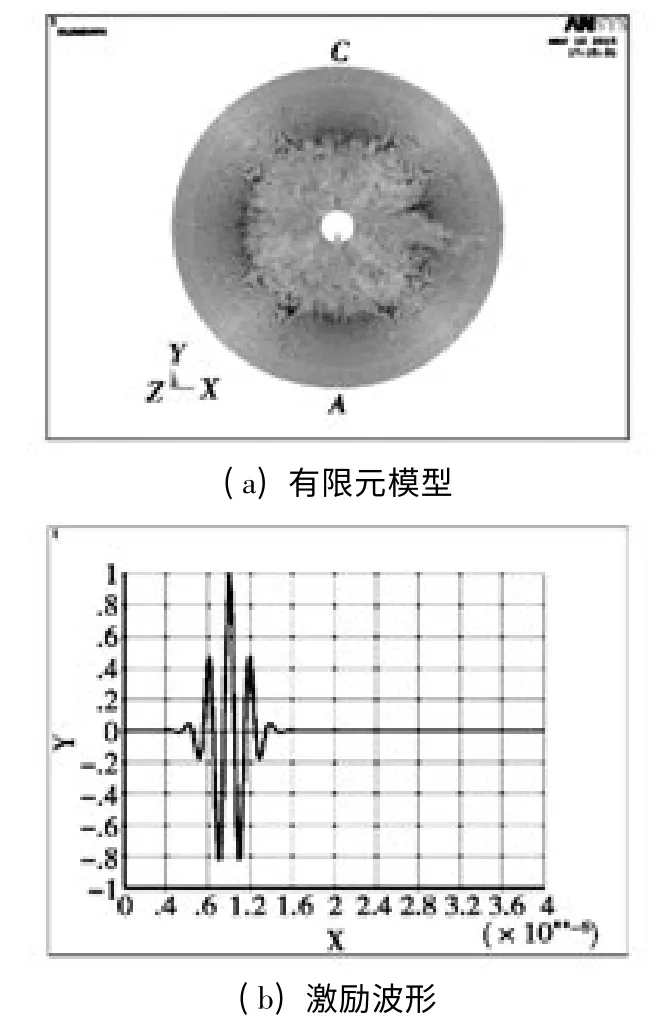
图4 有限元模型及激励

利用有限元模拟建立的模型参数与试验试件一致，也采用纵波垂直入射，其激励源为汉宁窗调制的信号，激励频率为2.5 MHz，与实验室探头发生的激励信号一致。激励波形如图4(b)所示。

在有限元计算中，从理论上讲，时间步长越小，计算结果越精确，但计算时间也相应增长。在本文中，根据所施加激励的中心频率，选用的时间步长为0.1 us。采用有限元的计算，2.5 MHz 的纵波在介质铝中传播过程的示意图如图5所示。

图5 纵波在介质中传播过程示意图

从图5 中可以看出，波在均匀的介质铝中传播，当没有遇到圆形缺陷时，是以常速度沿着固定的路线不受干扰地向前传播的，担当遇到圆形缺孔时，波的传播路线发生了变化，即在其他的、未受干扰的入射波的作用下，圆形的孔缺陷起到了一个次生波源的作用，形成了波的散射，而且波与它的原来路径发生了偏离，产生了衍射现象。

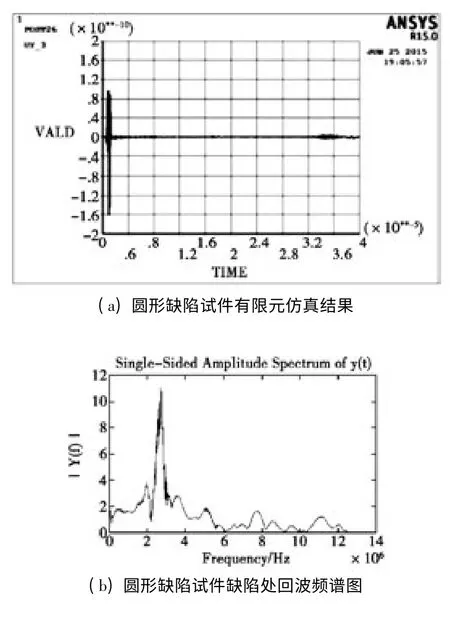
图6 有限元仿真时域图、频谱图

图6(a)(b)所示为图4(a)有限元模型中A 点的回波信号图，其中(a)图为有限元仿真结果图，(b)图为缺陷处回波频谱图。对比图3(a)(b)和图6(a)(b)，可以发现，有限元仿真结果图与实验采集的回波信号基本一致，由此可以验证仿真结果的准确性。

运用以上同样的方法，用有限元ANSYS 仿真槽形缺陷试件，得到的时域回波信号以及其缺陷处回波信号的频谱图，如图6(c)(d)所示。

对比图6 和图3，我们可以看出仿真结果和实验结果基本一致。对比图3(b)和图6(b)，图3(d)和图6(d)，我们可以看出，不同缺陷回波信号的频谱图是不一样的，因此，我们可以根据缺陷处的回波信号及其频谱图来判断试件中缺陷的位置、形状及大小。

4 结论

本文通过有限元法和实验法两种手段对铝圆柱体内缺陷进行检测，经过仿真结果与实验结果的对比，可以验证仿真结果的准确性。对缺陷处回波信号进行频域处理，对比不同缺陷回波信号的频谱图，可以看出缺陷的形状不同，其频谱图是可以明显看出不同的，因此，我们可以根据缺陷回波信号的频谱图，基本确定缺陷的形状。同时，我们也可以看出，ANSYS 能有效地仿真超声波的传播，构建超声场，表现超声场特性。因此在实际检测中可以用ANSYS 仿真超声波传播，对于开发研究超声波检测新技术来说，这点尤其重要，一方面通过仿真计算不断地修正设计参数，达到预期的设计效果;另一方面可以避免大量制作模拟试块进行检测验证;同时可以节约资金及时间，降低开发成本，提高开发效率，具有实用意义。

［1］张俊哲.无损检测技术及其应用［M］.北京:科学出版社，2010:1－2.

［2］Kosmatka B J，James M R.Damage Detection In Structures by Model Vibration Characterizati［J］.Journal of Structural Engineering，1999，12(12):1384－1392.

［3］顾雯琪，王召巴，陈友兴.基于Born 近似法的铝合金构件缺陷的三维反演［J］.激光与光电子学进展，2014，11:185－190.

［4］刘长福，牛晓光，李中伟，等.基于ANSYS 的超声纵_横波传播仿真计算［J］.无损检测，2008，30(6):15－18.

［5］张伟志，钢铁，王军.超声波检测计算机模拟和仿真的研究及应用现状［J］.应用声学，2003，3(1):41－46.

［6］郭文静，陈友兴，金永，等.基于多元高斯声束模型的圆柱体超声检测声场仿真［J］.应用声学，2013，32(5):354－360.

［7］Zheng Gangfeng，Wu Bin，He Cunfu Born.Inversion Technique for Ultrasonic Scattering Measurements［J］.Journal of Applied Sciences，2013，13(21):4399－4404.

［8］王勖成.有限单元法［M］.北京:清华大学出版社，2003:2－6.

［9］Hayashi T，Song W J，Rose J L.Guided Wave Dispersion Curves for a Bar Witan Arbitrary Cross-section a Rod and Rail Example［J］.Ultrasonics，2003，41:175－183.

［10］Yim H，Sohn Y.Numerical Simulation and Visualization of Elastic Waves Using Mass-Spring Lattice Model［J］.IEEE Trans UFFC，2000，47(3):549－558.