基于GM（1，1）模型的重庆市城镇化率预测研究

熊 遥，曾 波

（1.重庆工商大学长江上游经济研究中心，重庆 400067；2.重庆工商大学商务策划学院，重庆 400067）

中国经济发展呈现2个突出问题：地区发展不平衡和城乡差异大［1］。为了缩小城乡差距，中央城镇化会议指出城镇化可以推动中国的内生性改革。城镇化是推动中国经济持续发展的强劲动力［2］，而城镇化率是衡量一个地区经济发展水平的重要指标，目前国内外关于中国城镇化率的研究也非常多，有学者认为中国的城镇化率偏高。有学者于1999年提出20世纪90年代中国城市的“超常规发展”。高春亮［3］等于2013年提出中国城市的发展脱离了经济现实，城市发展过快。邓宇鹏［4］于1999年提出把乡镇企业和乡城流动人口算入城市人口，1997年中国的隐性城镇化率加上公开的城镇化率，实际水平超过60%。陆大道［5］于2007年提出城镇化脱离了中国经济社会发展的实际水平，实际城镇化率偏高。同时也有相当一部分学者认为中国城镇化率水平偏低。有学者于2001年提出与同期世界城镇化进程相比较，中国城镇化水平比世界城镇化平均水平低12个百分点。贾康［6］于2012年运用综合判断法提出中国城镇化水平仍较低，常住人口未能享受户籍人口相同的公共服务。许庆明［7］等于与2012年提出，通过沿海发达地区与法国、德国、意大利、日本、韩国比较，沿海发达地区城镇化水平与发达国家基本一致。

城镇化率最能反映一个国家地区的城镇化发展程度［8］。因此通过预测重庆市的城镇化率可以了解重庆市的城镇化发展趋势，为重庆市政府做决策提供依据，以促进重庆市的经济增长。

传统的城镇化率的预测方法有Logistic模型类——中国城镇化进程的S型曲线研究、城镇化与经济发展水平的相关分析法、时间序列分析类模型等，但是这些方法都存在缺陷。首先S型曲线形成需要一定的前提和时间跨度，中国的城镇化进程与S型曲线的应用条件相差甚远，用S型曲线来预测中国的城市化进程难以保证预测的科学性和精确性。其次，城市化与经济发展相关关系类模型考虑因素单一，没有包含政策等其他影响城镇化发展的因素。最后，时间序列分析类模型只反映社会经济现象动态变化的过程，而无法解释造成这一过程的原因，它适用于预测而不适用于解释［9］。

本研究提出应用灰色理论GM（1，1）模型对城镇化水平趋势进行预测。灰色系统理论着重研究概率统计、模糊数学等难以解决的“小样本”、“贫信息”不确定性问题，并依据信息覆盖，通过从已知数据中生成、开发和提取有价值的信息，实现对事物运动规律的探索［10］。另外，灰色系统理论对数据没有什么特殊的要求和限制，应用领域十分宽广。利用GM（1，1）模型进行城镇化率的预测研究不需要大量时间序列，也不需要分析影响城镇化的因素，研究过程简单，结果比较精确，能够有效预测城镇化率。因此利用重庆市的城镇化率的实际统计数据建立灰色预测模型，并对重庆市未来城镇化发展做出预测，以更好地了解重庆市的城镇化发展状况。

1 GM（1，1）模型

灰色系统基于序列算子的作用，通过对原始数据处理，挖掘其变化规律。GM（1，1）就是具体的挖掘数据的一种方法，通过建立GM（1，1）模型累加生成数据可以弱化数据的随机性，显现其规律性［11－14］。

1）设X（0）为非负序列X（0）＝（x（0）（1），x（0）（2），…，x（0）（n）），其中x（0）（k）≥0，k＝1，2，3，…，n；X（1）为X（0）的1－AGO 序列，X（1）＝（x（1）（1），x（1）（2），…，x（1）（n）），其中X（1）（k）＝∑k i＝1x（0），k＝1，2，…，n；Z（1）为X（1）的紧邻均值生成序列Z（1）＝（z（1）（2），z（1）（3），…，z（1）（n）），其中z（1）（k）＝0.5（x（1）（k）＋x（1）（k－1）），k＝2，3，…，n；GM（1，1）模型的基本形式为x（0）（k）＋az（1）（k）＝b，其中＝［a，b］T＝（BTB）－1BTY。

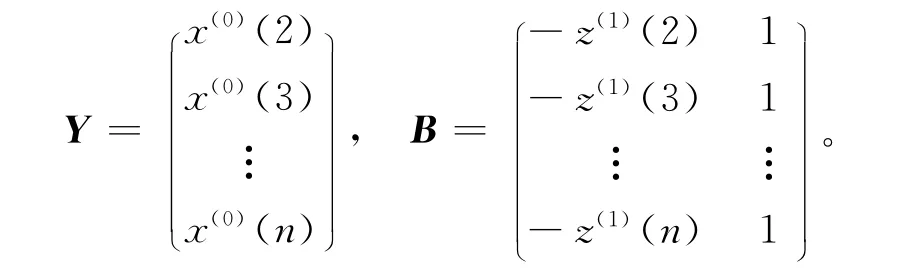
2）均值GM（1，1）模型的时间响应式为

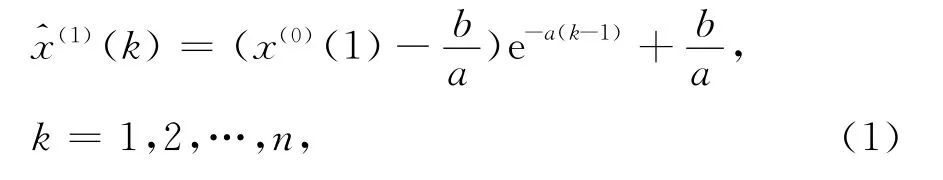
作累减还原生成，得还原数列

GM（1，1）模型是灰色系统理论最基本的研究方法，此方法是针对一个主导要素进行数据建模，并得出预测式进行数据预测，过程简单，预测结果精度高，可广泛用于少数据、贫信息的研究［15］。

2 重庆市城镇化率GM（1，1）模型的建立

本研究根据灰色系统理论GM（1，1）模型原理，建立重庆市城镇化率GM（1，1）模型，以R代表重庆市城镇化率变量，r代表重庆市城镇化率的具体取值。重庆市城镇化率的原始序列为R（0）＝（r（0）（1），r（0）（2），…，r（0）（n）），其中r（0）（k）≥0，k＝1，2，…，n；R（1）为R（0）的1－AGO 序 列，R（1）＝（r（1）（1），r（1）（2），…，r（1）（n）），其中R（1）（k）＝∑k i＝1r（0），k＝1，2，…，n；Z（1）为R（1）的紧邻均值生成序列：Z（1）＝（z（1）（2），z（1）（3），…，z（1）（n））， 其 中z（1）（k） ＝0.5（r（1）（k）＋r（1）（k－ 1）），k＝2，3，…，n； 由GM（1，1）模型的基本形式x（0）（k）＋az（1）（k）＝b可得重庆市城镇化率的GM（1，1）模型为r（0）（k）＋az（1）（k）＝b，其中＝［a，b］T＝（BTB）－1BTY。

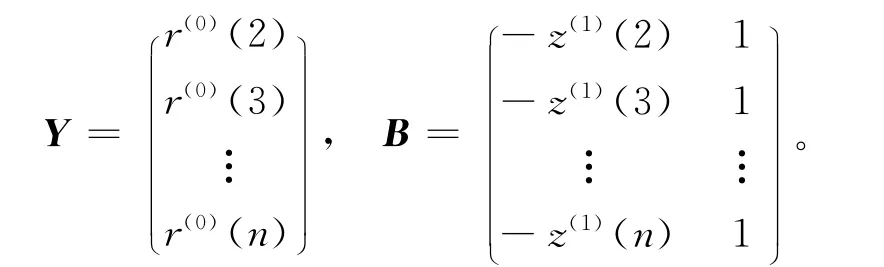
所以重庆市城镇化率的GM（1，1）模型的时间响应式为

作累减还原生成，得还原数列

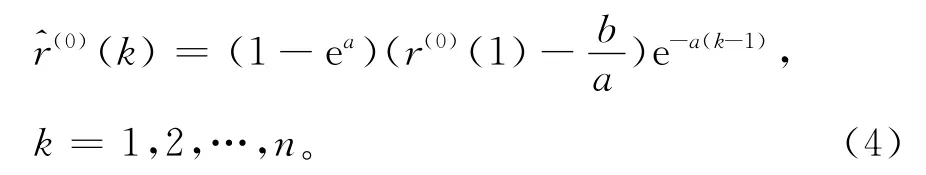
3 重庆市城镇化率GM（1，1）模型检验

一个预测模型是否有效，需要对该模型的模拟误差进行检验，只有通过了检验模型才能用于预测。本文通过4 种误差检验方式对重庆市城镇化率GM（1，1）模型的误差进行检验，包括平均相对误差检验、均方差检验、灰色绝对关联度检验和小误差概率检验［11－14］。

3.1 平均相对误差检验

原始数据序列R（0）＝（r（0）（1），r（0）（2），…，r（0）（n））；

残差序列为ε（0）＝ （ε（1），ε（2），…，ε（n））＝（r（0）（1）－（1），r（0）（2）－（2），…，r（0）（n）－（n））；

相对误差序列为

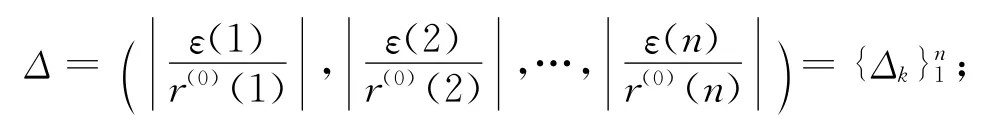
3.2 均方差检验

R（0）（k）的均值和方差s21分别为

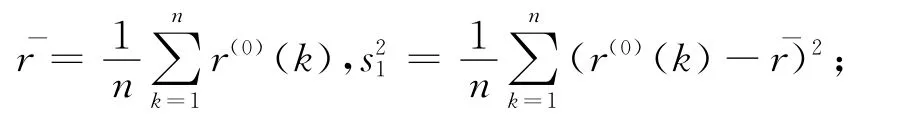
ε（0）的均值和方差s22分别为

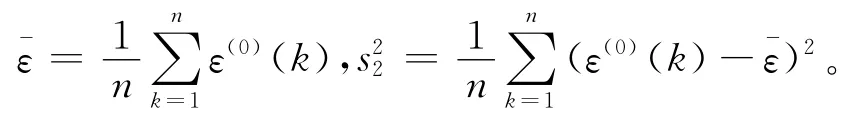
均方差比值为R＝s2／s1，给定r0，若R≤r0，则该模型为均方差比值合格模型。

3.3 灰色绝对关联度检验

R与的绝对关联度为ε，若给定ε0，ε≤ε0，则该模型为灰色绝对关联度合格模型。

3.4 小误差概率检验

p＝P（｜ε（k）－｜＜0.674 5S1）称为小误差概率，对于给定的p0＞0，当p＜p0，该模型为小误差概率合格模型。

4 重庆市城镇化率GM（1，1）模型的实际应用

4.1 模型构建

本研究取自2009—2013年5年的城镇化情况为原始数据，数据来源于重庆市2014年统计年鉴，包含的内容有常住人口、城镇、乡村和城市化率。但模型建立的原始数据仅需城镇化率即可，具体数据如表1所示。

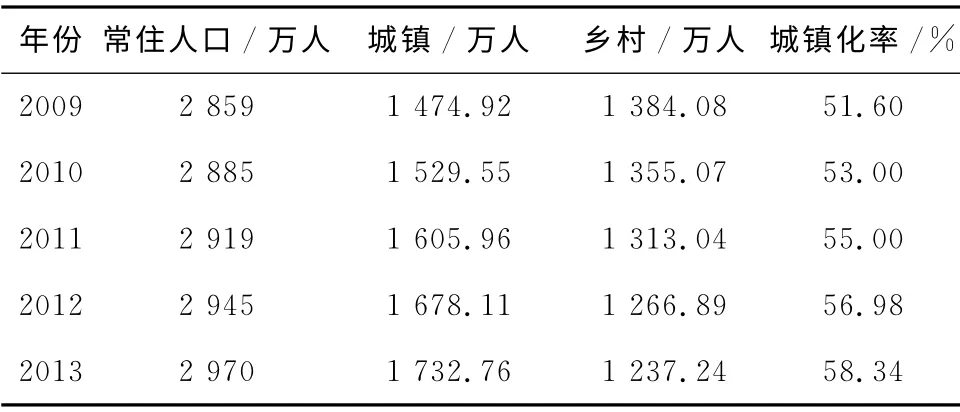
表1 重庆市2009—2013年城镇化情况表Tab.1 Urbanization situation of Chongqing in 2009—2013

R（0）＝ （51.6，53，55，56.98，58.34），R（1）为R（0）的1－AGO序列，则R（1）＝（51.6，104.6，159.6，216.58，274.92），R（1）均 值 生 成 数 据 为Z（1）＝（78.10，132.10，188.09，245.75）。

由重庆市城镇化率的GM（1，1）模型r（0）（k）＋az（1）（k）＝b，其中＝［a，b］T＝（BTB）－1BTY。

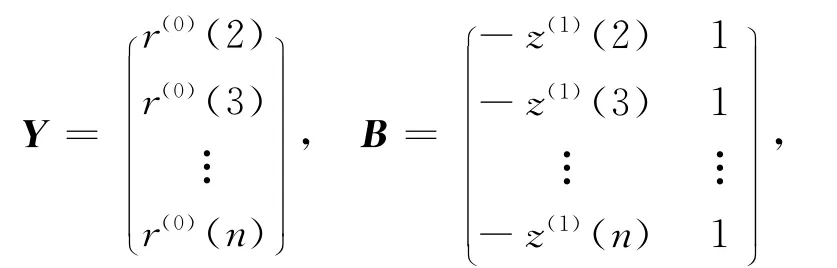
得a＝－0.032 2，b＝50.651 9。

由式（3）得重庆市城镇化率的均值GM（1，1）模型的时间响应式为

得

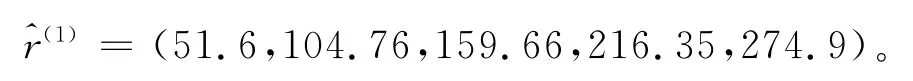
作累减还原，得

利用灰色预测模型软件可以得到原始序列和模拟序列对比图，如图1所示。

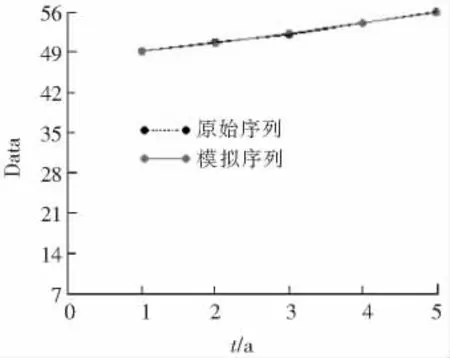
图1 原始序列和模拟序列比对图Fig.1 Comparison chart of original sequence and simulated sequence

4.2 误差检验

重庆市城镇化率的灰色模型为（k＋1）＝1 624.640 4e0.0322k－1 573.040 4，k＝1，2，…，n，模型是否成立，能否用于预测以及预测的精度高低还需进行检验，如果检验结果表明预测精度比较高，则可以用来对未来的城镇化率进行预测，反之不能用来进行有效预测。下面采用平均相对误差检验、均方差检验、灰色绝对关联度检验和小误差概率检验4种方法进行验证。

原始序列为

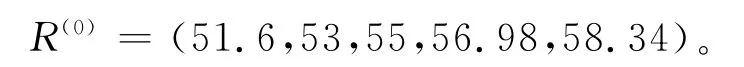
预测模型序列为

1）平均相对误差检验

残差序列：

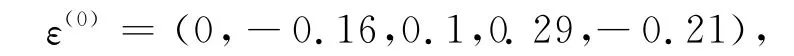
相对误差序列：

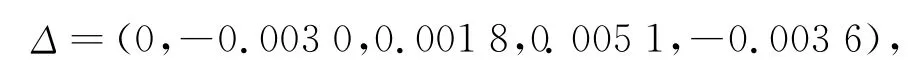
平均相对误差＝0.000 3，给定a＝0.005，因为Δ＝0.000 3＜0.01，精度为一级。

2）均方差检验

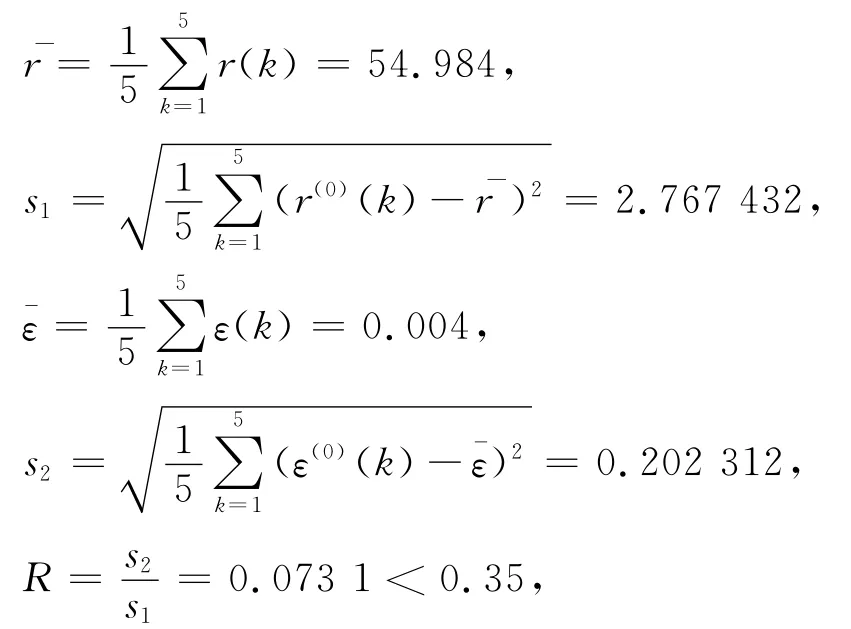
所以均方差比值为一级。

3）灰色绝对关联度检验

始点零像化得：

于是有：

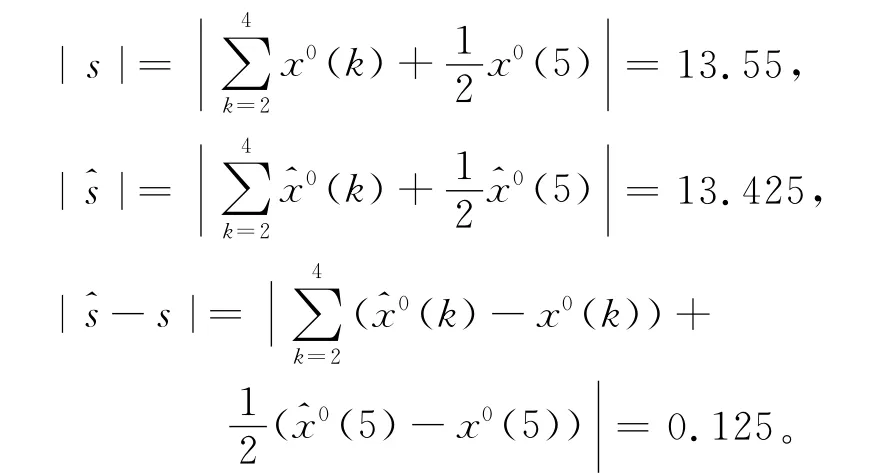
从而灰色绝对关联度为

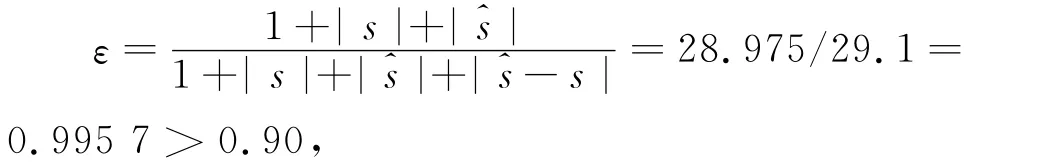
因此关联度为一级。

4）小误差概率检验

所以p＝P（｜ε（k）－｜＜0.674 5S1）＝1＞0.95，小概率事件为一级。

由误差检验结果并参照精度检验等级参照表（见表2），重庆市城镇化率GM（1，1）模型精度检验的结果为相对误差精度为一级，均方差比值为一级，关联度为一级，小误差概率为一级，因此重庆市城镇化率的灰色模型是成立的，可以用于预测，并且预测精度很高［11－14］（见表3）。

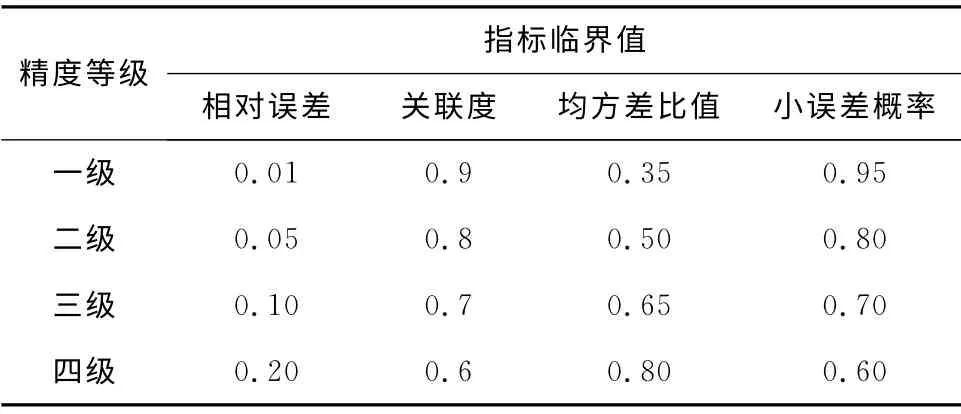
表2 精度检验等级参照表［11］Tab.2 Reference table for accuracy test level［11］

表3 重庆市城镇化率GM（1，1）模型精度检验［10］Tab.3 Accuracy test of Chongqing’s urbanization rate with GM（1，1）model［10］

4.3 重庆市城镇化率预测

重庆市城镇化率的GM（1，1）模型通过了平均相对误差检验、均方差检验、灰色绝对关联度检验和小误差概率检验，所以该模型可以用于对重庆市未来城镇化率的预测，现对重庆市未来5年的城镇化率进行如下预测。

由式（5）知：

当k＝5时，

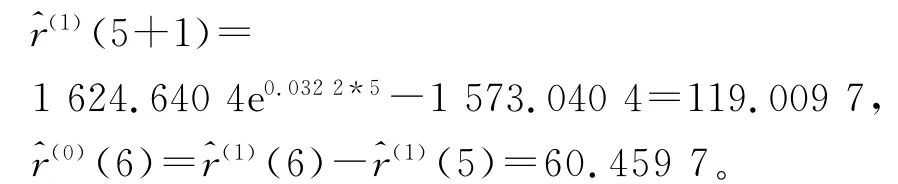
同理有：

当k＝6时，

当k＝7时，

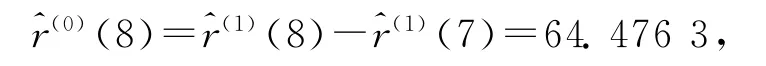
当k＝8时，

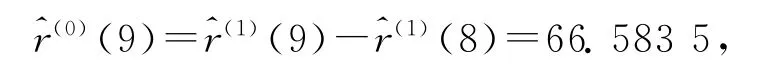
当k＝9时，

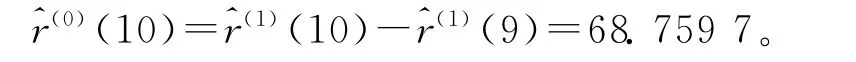
表4 重庆市未来5年城镇化率预测情况表Tab.4 Prediction table of Chongqing’s urbanization rate in the next five years

5 结 论

重庆市城镇化率的GM（1，1）模型通过了平均相对误差检验、均方差检验、灰色绝对关联度检验和小误差概率检验，所以该模型可以用于对重庆市未来城镇化率的预测［16］。

正在起草的《全国城镇化发展规划》已经初步明确了未来城镇化率的规划目标：2020年城镇化率达到60%左右。而经过研究发现，重庆市将在2014年达到这个目标，这个结果证明了重庆市城镇化率水平比较高，对中国的城镇化发展贡献比较大。现在应该保持重庆市的城镇化发展速度并尽量提高城镇化发展速度，以推进长江经济带的发展。

／References：

［1］ 黄凤彩.中国经济发展过程中的区域经济问题及解决对策［J］.吉林省教育学院学报（学科版），2009（6）：57－58.HUANG Fengcai.The regional economic problems and solutions through the economy development process of China［J］.Journal of Educational Institute of Jilin Province，2009（6）：57－58.

［2］ 王守智.从传统城镇化走向中国特色新型城镇化——基于科学发展观的分析视角［J］.河北科技大学学报（社会科学版），2014，14（1）：26－34.WANG Shouzhi.From the traditional urbanization to new urbanization with chinese characteristics：From the the perspective of scientific development concept［J］.Journal of Hebei University of Science and Technology（Social Sciences），2014，14（1）：26－34.

［3］ 高春亮，魏后凯.中国城镇化趋势预测研究［J］.当代经济科学，2013，35（4）：85－90.GAO Chunliang， WEI Houkai.Prediction study on the urbanization trends of China［J］.Modem Economic Science，2013，35（4）：85－90.

［4］ 邓宇鹏.中国的隐性超城市化［J］.当代财经，1999（6）：20－23.DENG Yupeng.Invisible super urbanization of China［J］.Contemporary Finance ＆Economics，1999（6）：20－23.

［5］ 陆大道.我国的城镇化进程与空间扩张［J］.城市规划学刊，2007（4）：47－52.LU Dadao.Urbanization process and spatial sprawl in China［J］.Urban Planning Forum，2007（4）：47－52.

［6］ 贾康.关于我国若干重大经济社会问题的思考（上）［J］.国家行政学院学报，2012（2）：16－22.JIA Kang.Reflections on a number of major economic and social problems in China［J］.Journal of Chinese Academy of Governance，2012（2）：16－22.

［7］ 许庆明，胡晨光.中国沿海发达地区的城市化与工业化进程研究——基于转型升级与国际比较的视角［J］.中国人口科学，2012（5）：14－22.XU Qingming，HU Chenguang.Urbanization and industrialization in developed coastal China：A global comparative perspective of transformation and upgrading ［J］.Chinese Journal of Population Science，2012（5）：14－22.

［8］ 余祥文.重庆城镇化发展特点分析［J］.合作经济与科技，2009（1）：11.YU Xiangwen.Analysis of the characteristics of the development of urbanization in Chongqing［J］.Co－Operative Economy＆Science，2009（1）：11.

［9］ 张佰瑞.城市化水平预测模型的比较研究——对我国2020年城市化水平的预测［J］.理论界，2007（4）：48－51.ZHANG Bairui.Comparative study on prediction model of city level：Prediction of city level in China in 2020［J］.Theory Horizon，2007（4）：48－51.

［10］ LIU Sifeng，LIN Yi.Grey Systems Theory and Applications［M］.Berlin：Springer，2010.

［11］ 刘思峰，谢乃明.灰色系统理论及其应用［M］.第6版.北京：科学出版社，2013.LIU Sifeng，XIE Naiming.Grey System Theory and Application［M］.6th ed.Beijing：Science Press，2013.

［12］ 刘思峰，杨英杰，吴利丰，等.灰色系统理论及其应用［M］.第7版.北京：科学出版社，2014.LIU Sifeng，YANG Yingjie，WU Lifeng，et al.Grey System Theory and Application［M］.7th ed.Beijing：Science Press，2014.

［13］ 刘思峰，党耀国，方志耕.灰色系统理论及其应用［M］.第5版.北京：科学出版社，2010.LIU Sifeng，DANG Yaoguo，FANG Zhigeng.Grey System Theory and Application［M］.5th ed.Beijing：Science Press，2010.

［14］ 曾波，孟伟，王正新.灰色预测系统建模对象拓展研究［M］.北京：科学出版社，2014.ZENG Bo，MENG Wei，WANG Zhengxin.Research on the Expansion of the Grey Prediction System Modeling of Object［M］.Beijing：Science Press，2014.

［15］ 张雅波.灰色预测的GM（1.1）模型［J］.吉林建筑工程学院学报，1999（4）：56－60.ZHANG Yabo.The GM（1.1）model of grey forecast［J］.Journal of Jilin Architectural and Civil Engineering Institute，1999（4）：56－60.

［16］ 刘思峰，邓聚龙.GM（1，1）模型的适用范围［J］.系统工程理论与实践，2000（5）：121－124.LIU Sifeng，DENG Julong.The range suitable for GM（1，1）［J］.Systems Engineering－Theory ＆ Practice，2000（5）：121－124.