高原型风力发电机组的变桨控制
林志明,莫尔兵,宋聚众,许娟
(东方电气风电有限公司,四川德阳,618000)
高原型风力发电机组的变桨控制
林志明,莫尔兵,宋聚众,许娟
(东方电气风电有限公司,四川德阳,618000)
针对高原型变速变桨风力发电机组在额定风速附近容易失速,在额定风速以上载荷较大的问题,提出在额定风速以下根据叶片气动特性进行变桨微动控制,通过变桨动作,调整叶片攻角使其远离失速点;在额定风速以上时提出桨距角纹波技术,通过在传统桨距角给定信号上叠加纹波信号间接加大塔架一阶振动模态的阻尼,避免塔架顶部的大幅度振动位移。通过Bladed软件对提出的变桨控制方式进行仿真分析,结果表明:相对传统的变桨控制方式,提出的额定风速以下变桨微动控制能有效地避免风电机组失速;提出的桨距角纹波技术能增加塔架一阶振动模态的阻尼,有效地减小风电机组在额定风速以上发电时塔架顶部的振动位移,降低塔架的疲劳载荷。
高原型,变速变桨,变桨控制,失速,机组疲劳载荷
0 引言
目前变速变桨风电机组已成为市场的主流形式,这种机组在低风速时按照最佳叶尖速比运行,追踪最佳风能利用系数Cp,风能利用率较高,高风速时通过变桨限制气动力矩,恒定功率输出,具有发电量高、载荷小、功率品质好等优点。近几年,随着市场上变速变桨风电机组数量的倍增以及风资源的大规模开发,国内风资源较丰富且可开发的风电场越来越少,因此大多数整机厂商开始关注高原型、弱风型风力发电机组的开发,风轮直径越来越大,塔架高度越来越高,导致机组的载荷也越来越大,高原上低空气密度导致的叶片失速问题也时有出现。而对于如何通过变桨控制解决此类问题,实现机组性能的优化,目前有少数文献提出利用独立变桨技术来进行机组载荷优化[1-2], 也有少数文献提出利用智能控制或自适应控制技术来优化机组的输出功率[3-5],而大多数关于变桨方面的文献涉及的都是变桨系统的建模及其控制系统的实现和优化方式[6-8],实际上,在风电机组的整个控制系统中,变桨系统只是一个执行机构,在系统设计时,可将其线性化为一个低通滤波器,如何给定低通滤波器 (变桨系统)的输入才是变速变桨风电机组变桨控制的重点。
变速变桨风电机组通常有双馈式和直驱式2种[9],而两者却具有共同的控制特点:低风速时桨距角限制在某一最优值 (比如0°),尽可能吸收功率,在高风速时通过变桨控制调整桨叶攻角限制功率,以使机组结构载荷不至于超出设计值。本文首先简要地阐述了叶片的气动特性,指出高原型风电机组在低空气密度区域容易在额定风速附近失速,同时引入变桨微动控制方式,并且提出利用桨距角纹波技术,降低机组关键部位的疲劳载荷,同时借助某双馈式2.0 MW机组,通过Bladed软件仿真比较,验证了本文提出的变桨控制的优越性。
1 额定风速以下防止失速的变桨微动控制
1.1 叶片的空气动力学
1.1.1 攻角的概念
叶片翼型的攻角是用来描述叶片气动特性的物理量,是来流速度方向与叶片翼型弦线之间的夹角[10]。假定叶片处于均匀来流速度V∞(1-a)中同时风轮以角速度Ω旋转,则叶片半径r处的翼型所受的力如图1所示。
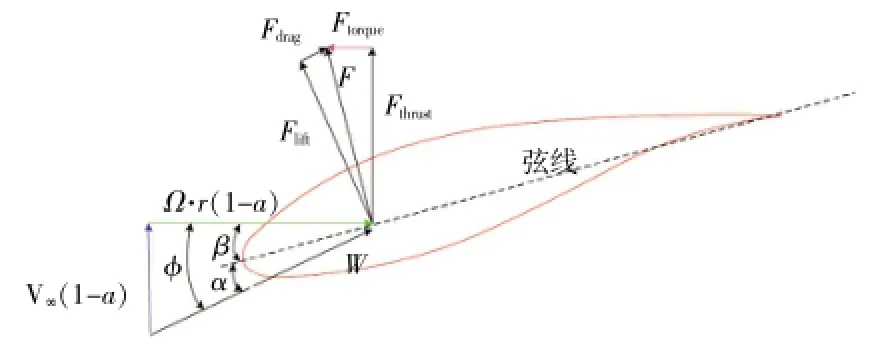
图1 叶片翼型的气动特性
合成后的来流速度W与风轮旋转平面之间的夹角为Φ,β为桨距角,则翼型的攻角为:
α=Φ-β (1)
在叶片半径r与δr范围内所受到的与来流速度方向W垂直的升力[11]为:
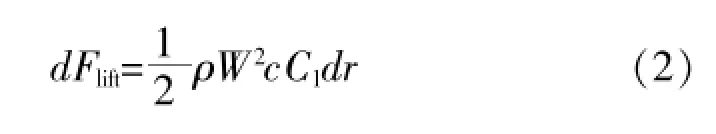
与来流速度方向W平行的阻力[11]为:
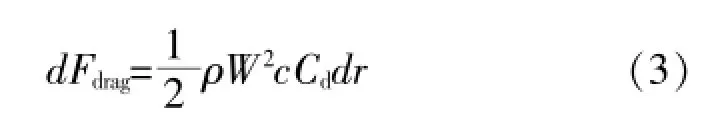
式(2)、(3)中,ρ是空气密度;c是叶片半径r处的翼型弦长;Cl是翼型的升力系数;Cd是翼型的阻力系数。
1.1.2 翼型的失速特性
由式(2)、(3)可以看出,翼型的升力与阻力除了与空气密度和来流速度W有关外,还与翼型本身的升力系数Cl和阻力系数Cd有关,不同的翼型有不同的升力系数和阻力系数,典型的升、阻力系数曲线如图2所示[12]。
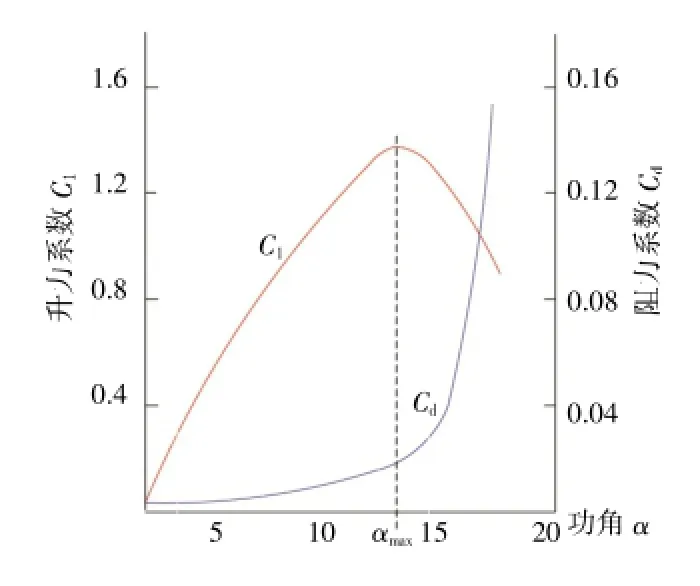
图2 翼型的升力系数和阻力系数曲线
由图2可以看出,当攻角超过αmax后,升力系数迅速减小,而阻力系数迅速增大,导致翼型的升力迅速下降,阻力迅速上升,该点称为“失速点”。
实际上,无论是定桨失速型风力发电机组还是变速变桨型风力发电机组,其叶片都存在着失速特性,只不过前者恰恰利用了这一失速特性来限制额定风速以上的功率吸收,而后者则需要在额定风速以上不断调整攻角来避开其失速点以维持额定功率的平稳输出。
1.2 额定风速以下的变桨微动控制
1.2.1 高原型风力发电机组的失速
变速变桨型风力发电机组的叶片在设计时通常都能保证机组在额定风速附近偏离失速点,但是由于高原上空气密度稀薄,气流中所蕴含的能量少,风力发电机组要达到额定功率所需要的风速要比标准空气密度下高得多,由于在额定风速以前,变速变桨型风力发电机组的风轮转速已经达到上限,传统的变桨控制通常将桨距角维持在最佳桨距角位置,如0°,并且保持不变,因此,随着风速的增加,图1中的Φ角逐渐增大,而桨距角β此时通常保持不变,则攻角α不断增大,最终导致叶片的攻角超过 “失速点”,引起风力发电机组失速。
当机组在运行中出现失速以后,噪声常常会突然增加,而且还会引起机组振动以及运行不平稳等现象。因此需要避免变速变桨型风力发电机组在任何情况下出现失速。
某双馈式机组额定风轮转速15.13 r/min,额定功率2.0 MW,额定风速10.2 m/s,图3是该机组在标准空气密度和0.78 kg/m3空气密度下产生的功率曲线对比。
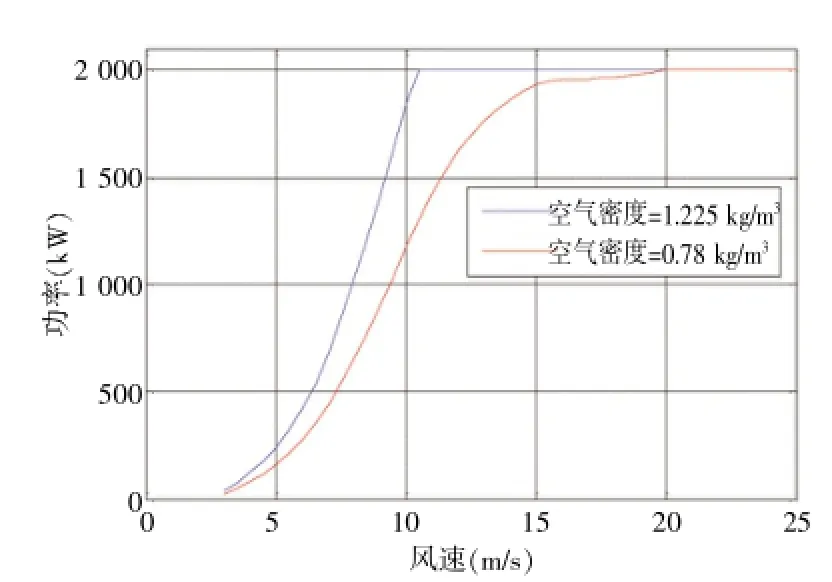
图3 某双馈式机组在不同空气密度下的功率曲线
由图3可以看出,在标准空气密度下,机组在风速10 m/s左右便已达到额定功率,而在空气密度只有0.78 kg/m3的情况下,即使风速达到18 m/s也达不到额定功率,这是因为叶片在风速15 m/s附近便已出现失速现象。
对于已经投入运行的高原型风力发电机组,如果出现失速现象,则从图1中,不难得出解决失速问题的办法:
(1)提高风轮叶尖速度,减小Φ角。这可以通过提高发电机额定转速、加大风轮直径以及减小齿轮箱速比来实现;
(2)降低机组额定功率,提前达到满负荷,实现变桨动作。如可将额定功率2.0 MW的机组降容到1.7 MW使用,则由图3可知,机组在风速达到11 m/s左右便已达到额定功率1.7 MW,此时机组并不会失速,而此后机组必会调节桨距角限制功率,也不会出现失速现象;
(3)机组达到额定功率之前提前增大桨距角β。
对于第(1)点,由于电机、变频器等方面的电气限制,往往很难再提高发电机的额定转速,另外,更换叶片和齿轮箱都会直接导致维护成本大幅增加;第(2)点对年发电量损失较大;而第(3)点只需要修改控制策略,不会增加任何成本。
1.2.2 变桨微动控制方式
本文提出在额定风速以下便开始进行变桨微动调节,增大桨距角β,使得叶片翼型的升力系数在高风速下且机组未达到额定功率之前仍然可以保持在线性范围之内,这能有效地解决高原型风力发电机组的失速问题。根据简化的风力机理论,叶片半径r处的入流倾角[11]为:
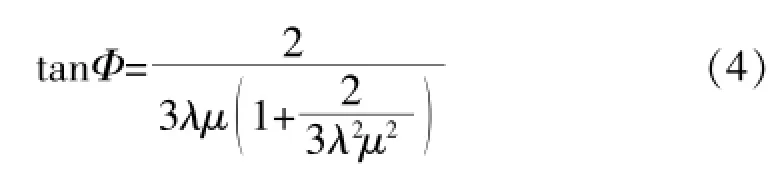
式中,λ为叶尖速比,μ=r/R,R为风轮半径,Φ与λ之间的关系近似反函数,如图4所示。
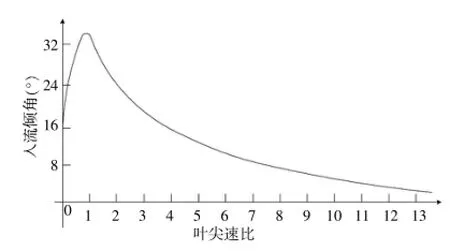
图4 翼型入流倾角与叶尖速比之间的关系
为了避免叶片失速,攻角需满足式(5)[11]。

由式(4)、(5)即可得到桨距角需要满足的关系:
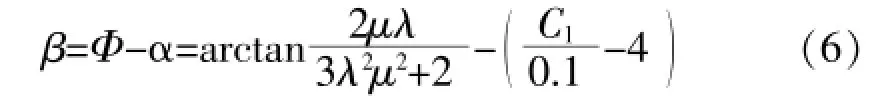
对于具有特定桨叶的风力发电机组,风轮半径R确定,其翼型的升力系数Cl也可以确定,因此可以利用式(6)根据当前的叶尖速比调整桨距角使叶片远离失速区。
变桨微动控制的控制器结构如图5所示。一般的PI控制器都要对其输出进行限幅,传统变桨控制将PI输出的最小值限制在最佳桨距角位置(如0°),将最大值限制在顺桨位置 (如90°),而从图5可以看出,变桨微动控制方式将按式(6)对PI的输出下限进行限制,一旦β>0之后,变桨系统便能及时响应,实现提前变桨。
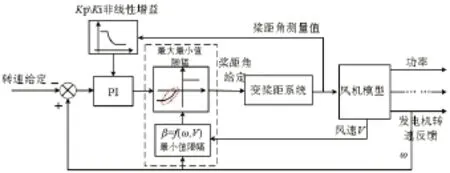
图5 变桨微动控制结构
2 高风速时载荷优化的变桨控制
2.1 控制目标
对于大型变速变桨风力发电机组,2个主要的控制目标一个是捕获尽可能多的能量,另一个就是尽可能降低关键部位的载荷,例如塔架载荷,传动链载荷等。因为塔架成本在整个风电机组中占有相当大的分量,所以尽可能地降低塔架载荷,对于降低机组成本、提高机组性价比具有重大意义。
本文在分析塔架振动模态的基础上,指出塔架振动的模态阻尼很小,在正常湍流风作用下塔架顶部振幅较大,容易引起塔架疲劳载荷的增加。随后提出利用桨距角纹波技术改变风轮推力加大塔架一阶振动模态阻尼,这种控制方式在不增加任何成本的基础上能有效地降低塔架的疲劳载荷,降低机组设计成本,提高机组性价比。
2.2 塔架振动模型
将钢管式塔架看成一个质量为m、长度为h的悬臂梁,将机舱和风轮等效成一个质点M,则典型的塔架模型如图6(a)所示。
忽略偏航、塔架高阶模态的影响,可将塔架的振动问题简化为一个单自由度系统的强迫振动,根据图6(b)可得系统的运动微分方程为:

式中,M'为塔架的等效质量与机舱的等效质量之和,有M'=M+0.23 m[13];K为塔架等效刚度,根据振动力学[14-15],有K=3EI/h3;D为塔架等效阻尼系数;x是塔架顶部的振动位移;Fthrust为风轮所受到的推力。
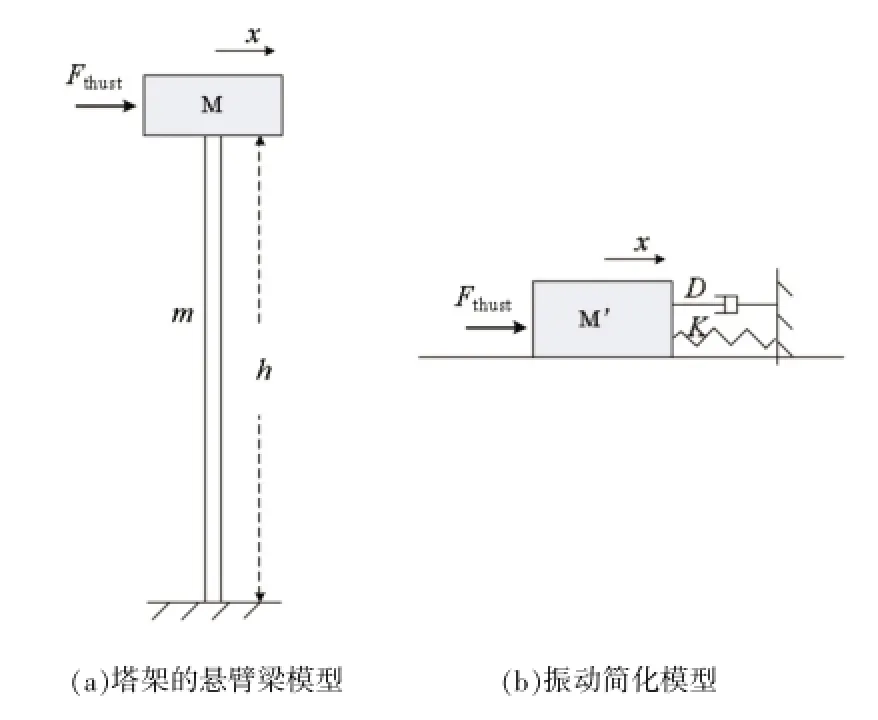
图6 典型的塔架模型
以某双馈式2.0 MW机组为例,从图7所示的坎贝尔图中可得知塔架的一阶模态阻尼系数D很小,仅为0.082。由振动理论可知,阻尼小的系统响应幅值大,衰变慢,而对于风电机组中的塔架在风轮推力作用下容易引起顶部的振动位移幅值偏大,引起塔架疲劳载荷的大幅度增加,故系统设计时要尽量加大塔架模态阻尼。
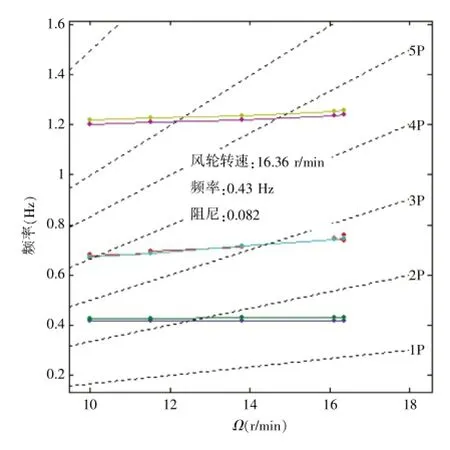
图7 某双馈式机组坎贝尔图
由图1可知,风轮推力与风轮平面垂直,与升力Flift之间的夹角为Φ,因此β与风轮推力之间存在紧密关系,如果能通过调整桨距角,使得在风轮推力Fthrust的基础上产生一个额外的力ΔFthrust,且ΔFthrust=-kx˙,则有:
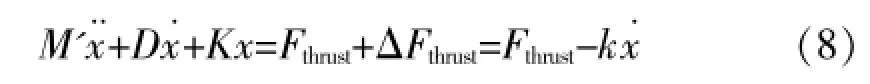
因此,运动方程可以变为:
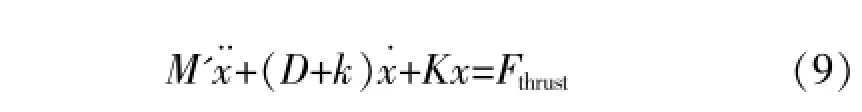
显然,塔架的等效阻尼从D增加到了 (D+ k)。
而ΔFthrust与-kx˙之间满足如下关系:

因此有:
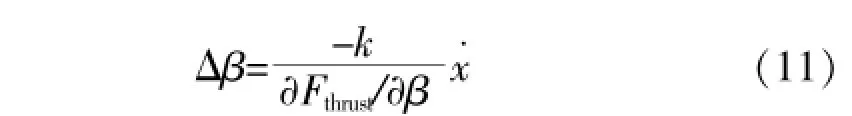
2.3 塔架阻尼器的设计
由式(11)可知,要想通过调节桨距角增加塔架一阶模态的阻尼,必须测出塔架顶部的振动速度x˙,而在实践工程当中,测量塔架顶部的振动加速度要比测量振动速度简单得多,只需要在塔架顶部安装振动加速度传感器即可。通过对振动加速度x¨的积分得到振动速度x˙。因此可设计塔架阻尼器结构如图8所示。
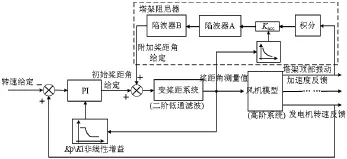
图8 塔架阻尼器结构图
图中陷波器A是用来校正相位的,陷波器B用来屏蔽桨叶穿越频率3P、6P等的影响,形式为:
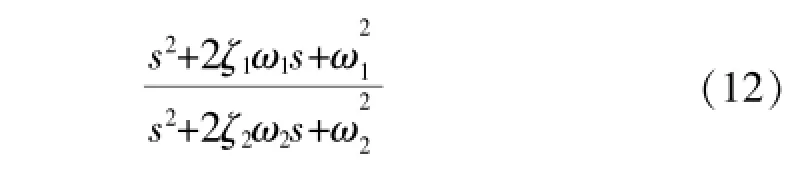
加入塔架阻尼后,从风速给定到塔架顶部振动速度之间的频域特性如图9所示。
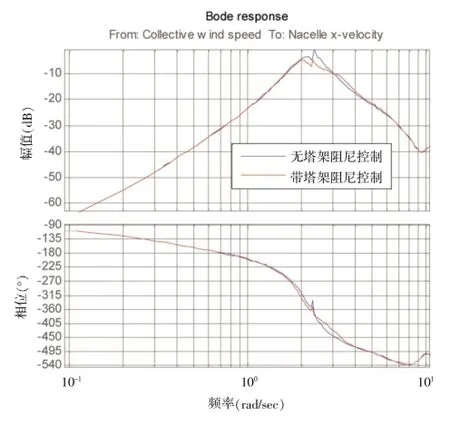
图9 某双馈式机组塔架顶部振动特性
由图9可以看出,在加入塔架阻尼控制之后,在塔架一阶振动模态频率附近,机舱顶部的振动速度幅值有所减小,说明塔架阻尼起到了一定的作用。
在风速的单位阶跃给定下,桨距角响应和塔架顶部振动位移的响应分别如图10、图11所示。
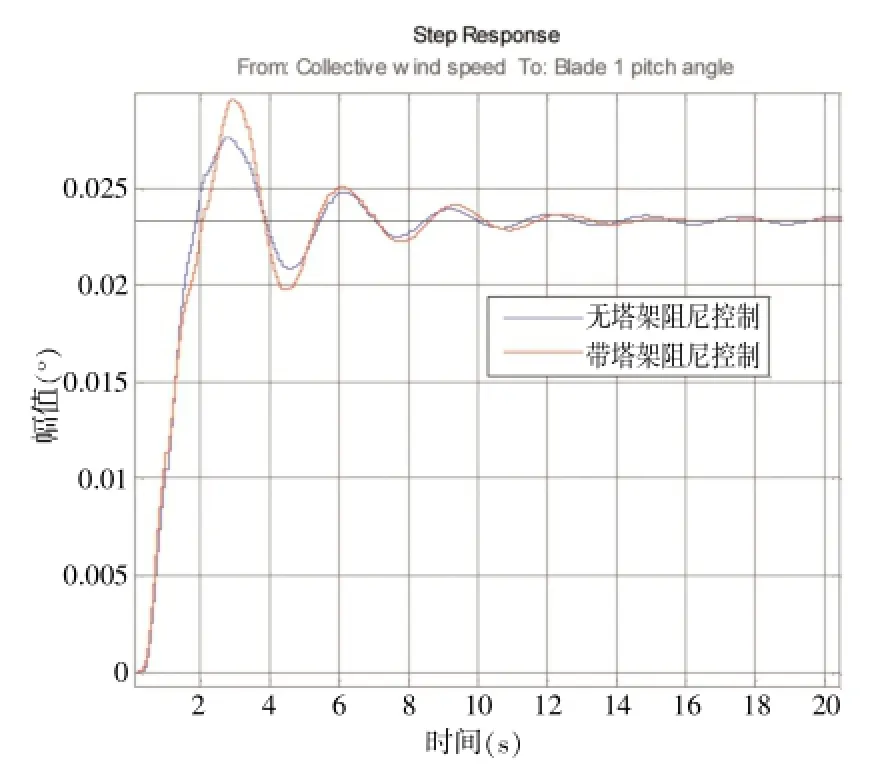
图10 某双馈式机组桨距角在单位阶跃风速下的响应
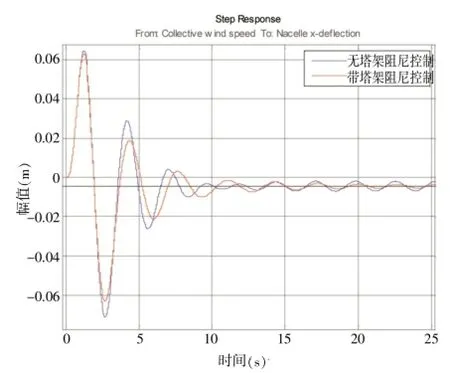
图11 某双馈式机组塔架顶部振动位移在单位风速阶跃下的响应
由图10、图11可以看出,系统在加入塔架阻尼后,在单位风速阶跃给定下,桨距角的单位阶跃响应超调量有所增加,说明变桨系统比之前要有更多的变桨动作,而塔架顶部振动位移的响应幅值有所减小,而且响应比之前衰减得更快,说明塔架阻尼确实有所增加,经过进一步的仿真分析可得,塔架一阶模态的阻尼由之前的0.082增加到0.267,证明桨距角纹波信号在增加塔架阻尼方面效果良好。
3 仿真结果
3.1 变桨微动控制在改善叶片失速方面的优越性
本文借助Bladed软件进行机组的失速特性研究和疲劳载荷计算。
某高原型双馈式机组在空气密度为0.78 kg/m3的风场曾出现失速现象,因此选取该空气密度对2种控制方式进行仿真分析。为了便于比较,仿真中采用静态风速,结果如图12所示。
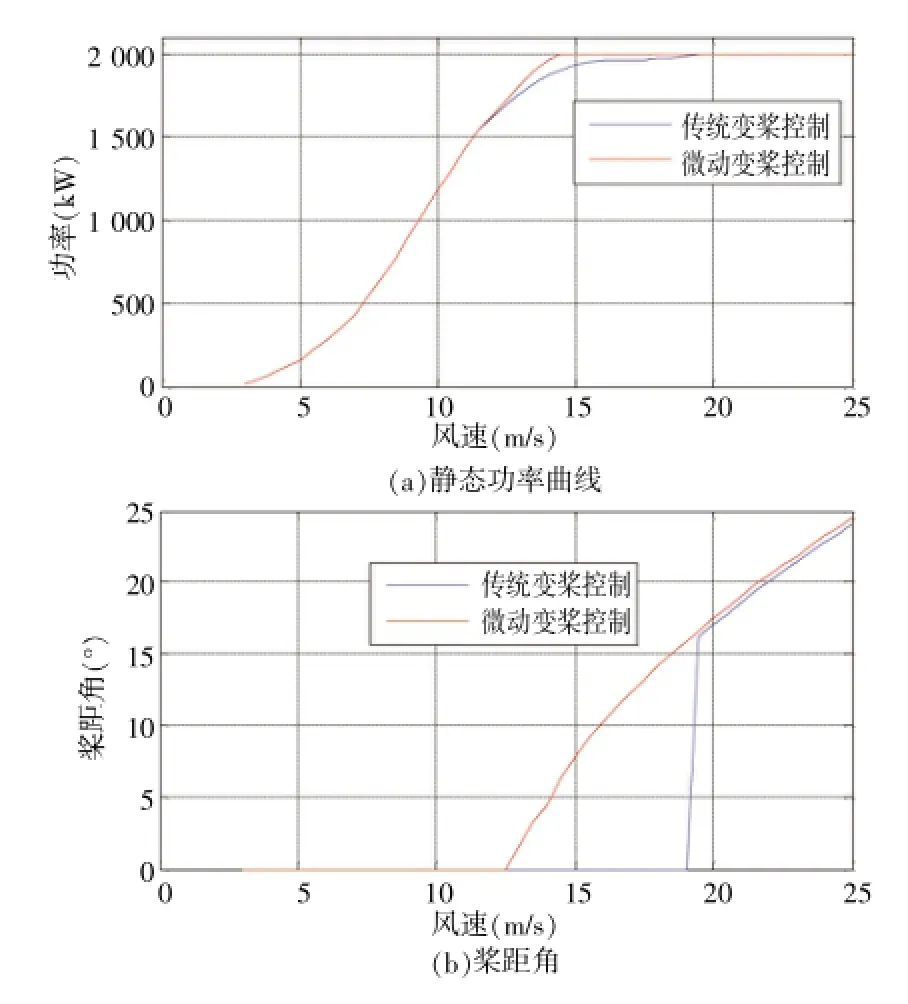
图12 2种控制方式静态功率曲线比较
由图12可以看出,机组在低风速段功率曲线一致,这是因为在低风速情况下,叶片并不会失速,2种控制方式的桨距角都维持在0°,追求最佳Cp曲线。在风速达到13 m/s左右,变速阶段已经结束,风轮转速已经达到额定转速,传统的变桨控制方式因为功率未达到额定功率,因此要维持桨距角在0°,叶片开始失速,此后风速越大,叶片失速越严重,而此时变桨系统又不会主动进行变桨,叶片失速后机组噪音变大,严重时导致机组剧烈振动;而变桨微动控制方式在风速13 m/ s,功率未达到额定功率2.0 MW时便开始主动增大桨距角,减小翼型的攻角,有效地避免了叶片失速。在变桨微动控制方式下,机组在14 m/s风速下便达到额定功率。因此,相比较于传统的变桨控制方式,低空气密度时变桨微动控制在防止叶片失速方面有一定的优越性。
3.2 高风速时有、无塔架阻尼的载荷比较
图13是针对某双馈式机组有、无载荷优化控制时的仿真结果。因为载荷优化的效果体现在额定风速以上的各个工况下,所以本文根据GL标准取DLC1.2下18 m/s时的仿真结果作比较。
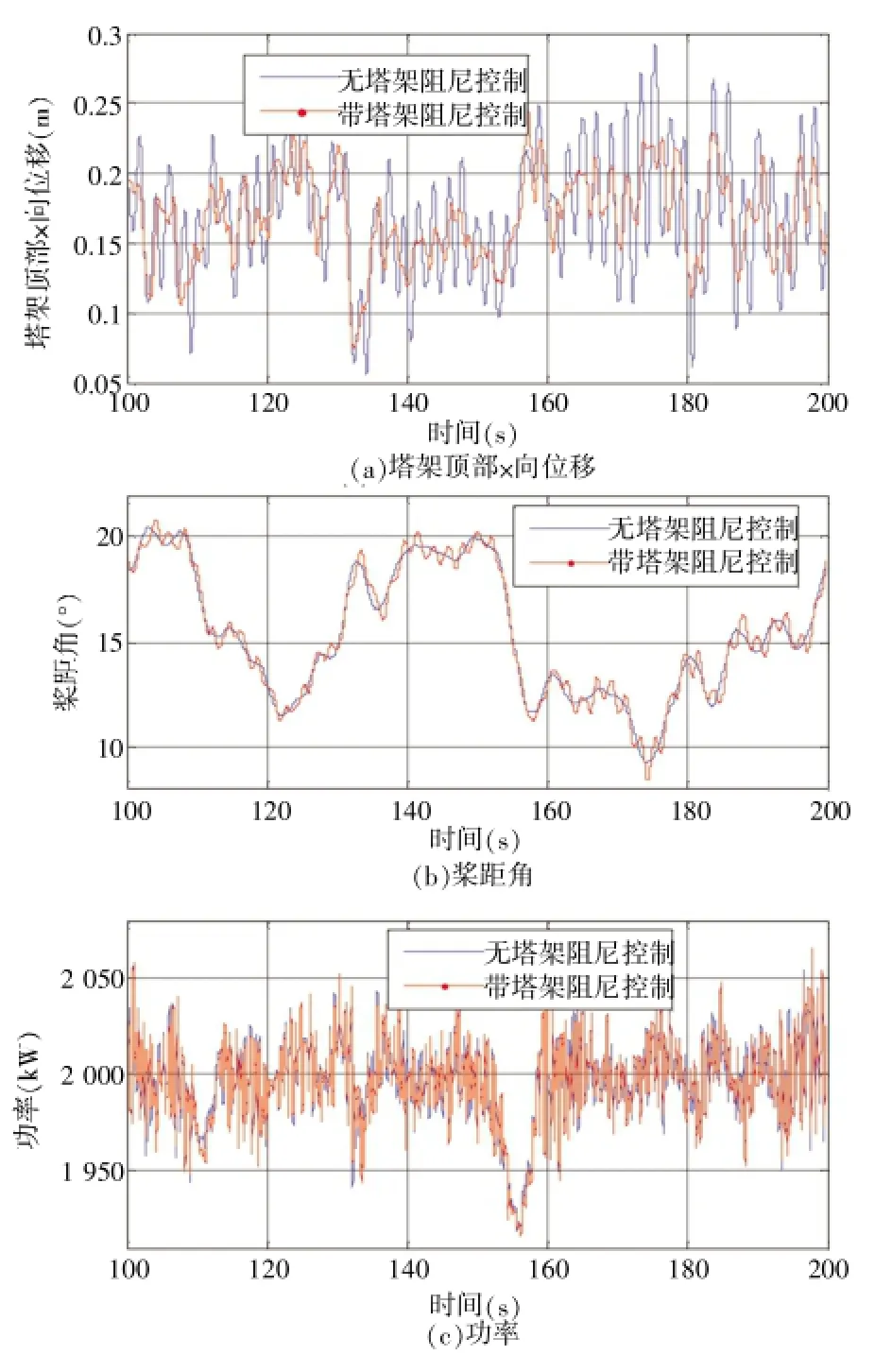
图13 某双馈式机组有无塔架阻尼器仿真结果
从仿真结果中可以得出,在加入塔架阻尼之后,塔架顶部x方向振动位移变小,如图13(a)所示,这是因为在传统变桨控制方式的桨距角给定信号上叠加了桨距角纹波信号,因此随之而来的是变桨系统的频繁动作,如图13(b)所示,而从图13(c)中可以看出,发电功率在2种控制方式下差别不大,功率品质并没有因为频繁的变桨动作而变差。
由于桨距角纹波信号在整个变桨控制环节中相当于扰动信号,因此会在一定程度上影响着系统的稳定性,在设计时不可一味地加大塔架阻尼,必须以保证变桨控制环节的稳定性为前提。图14是加入塔架阻尼控制后变桨控制环节的开环Bode图,该图说明了在加入塔架阻尼控制后并没有影响该环节的稳定裕量。
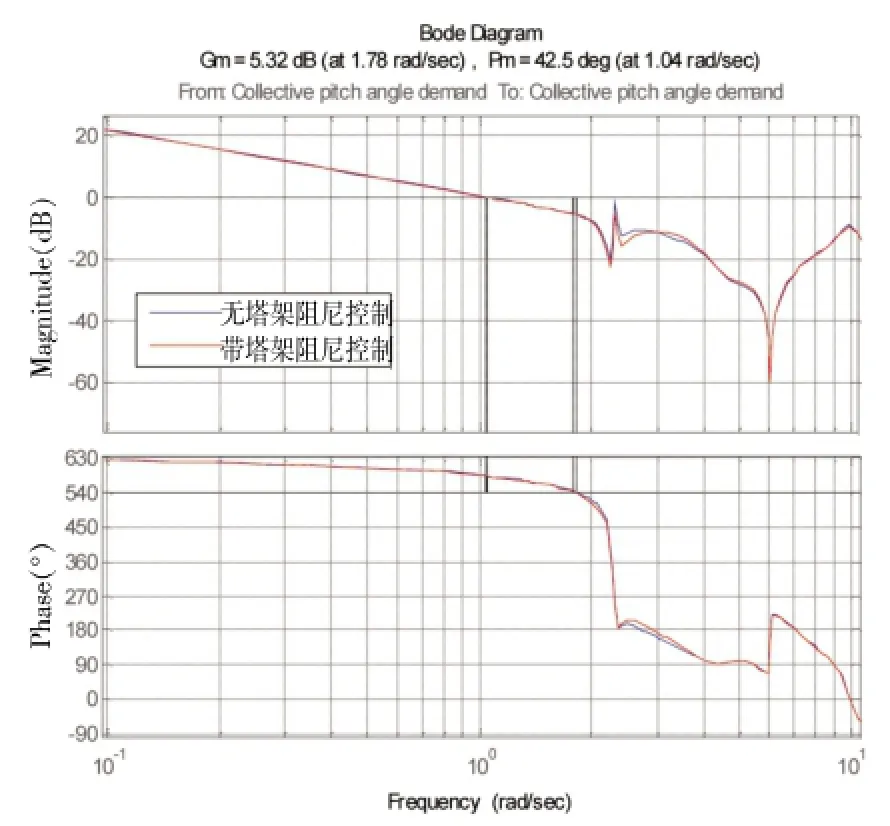
图14 某双馈式机组有无塔架阻尼时变桨控制环节稳定裕量
另外,由于变桨系统的频繁动作会在一定程度上影响变桨轴承的疲劳寿命,而且还容易导致变桨电机过热,因此在设计塔架阻尼时,需要权衡变桨轴承疲劳载荷、电机过载能力与塔架疲劳载荷之间的矛盾,也需要考虑桨距角的频繁变化与变桨系统响应能力之间的关系。
通过Bladed软件仿真可以定量地得出,在加入塔架阻尼之后,塔架顶部My方向和偏航轴承Mxy方向的疲劳载荷降低幅度较大,在8%以上,塔架底部My方向疲劳载荷降低约5%,说明在加入塔架阻尼之后有效地降低了机组关键部位的疲劳载荷,降低了成本,提高了机组的性价比。
4 结论
本文在分析高原型变速变桨风电机组在低空气密度下容易失速的基础上,提出了某双馈式机组在未达到额定功率之前采用变桨微动控制方式提前调节桨距角,使得叶片翼型在高风速下都能保持合理的攻角,避免叶片失速;同时指出在塔架一阶模态阻尼较小并且在湍流风作用下塔架顶部容易产生较大振动位移的情况下,采取在传统的变桨给定信号上根据塔架顶部的振动加速度信号叠加桨距角纹波信号,降低塔架疲劳载荷。仿真结果表明:变桨微动控制方式能有效避免风电机组在低空气密度下失速,叠加的桨距角纹波信号能降低关键部位疲劳载荷5%以上。
[1]刑作霞,陈雷,孙宏利,等.独立变桨距控制策略研究[J].中国电机工程学报,2011,31(26):131-138
[2]姚兴佳,马佳,郭庆鼎.基于模糊控制的风电机组独立变桨距控制[J].可再生能源,2011,29(06):34-38
[3]姚兴佳,张雅楠,郭庆鼎.风力发电机组的多模变桨距控制[J].沈阳工业大学学报,2009,31(02):149-153
[4]夏长亮,宋战锋.变速恒频风力发电系统变桨距自抗扰控制[J].中国电机工程学报,2007,27(14):91-95
[5]何玉林,吕向飞,黄帅,等.变速变桨风力发电机组的优化控制[J].可再生能源,2012,30(01):33-37
[6]王佳雯,龚华军,陈永.大型风力发电机组变桨距控制系统设计与仿真[J].电气自动化,2011,33(05):18-21
[7]孟彦京,常杰,朱玉国.风力发电变桨控制系统设计[J].电气传动,2010,40(05):41-43
[8]窦真兰,程孟增,蔡旭,等.大型风机变桨距控制系统的研究[J].电机与控制应用,2011,38(03):38-43
[9]李建林,高志刚,付勋波,等.几种典型的风力发电系统对比分析[J].电源技术应用,2007,10(9):54-60
[10]叶杭冶.风力发电机组的控制技术[M].北京:机械工业出版社,2006:14-33
[11]Tony B,David S,Nick J,et al.Wind Energy Handbook [M].Chichester:John Wiely&Sons,Ltd.,2001:41-77
[12]van der Hooft E L,Schaak P,van Engelen T G.Wind turbine control algorithms[M].Holland:Dutch Ministry of Ecnomic Affairs,2003:22-31
[13]何显富,卢霞,杨跃进,等.风力机设计、制造与运行[M].北京:化学工业出版社,2009:224-225
[14]闻邦椿.机械设计手册[M].北京:机械工业出版社,2010: 1-123-1-147
[15]高淑英,沈火明.振动力学[M].北京:中国铁道出版社, 2011:09-30
Pitch Control of Plateau Type Variable Speed Variable Pitch Wind Turbine
Lin Zhiming,Mo Erbing,Song Juzhong,Xu Juan
(Dongfang Electric Wind Power Co.,Ltd.,Deyang Sichuan,618000)
For plateau type VSVP(variable speed variable pitch)wind turbine which is very easy to stall around rated speed and often generate large loads above rated speed,a micro-motion pitch control scheme around rated speed is proposed to modify the attack angle of airfoil according to its aerodynamic characteristics,so that the attack angle of airfoil can be far away from stall zone.A pitch ripple control scheme adopted here can increase the tower damper indirectly by adding a ripple signal to the original pitch angle,which can avoid large loads and decrease tower top vibration displacement above rated speed.Comparing Bladed simulation results of the pitch control scheme here with the traditional pitch control's,the way of pitch control presented here can avoid stall in low air density zone around rated speed,and can also reduce the load of some crucial parts of the turbine above rated speed.
plateau type,variable speed variable pitch,pitch control,stall,turbine fatigue load
TP273
A
1674-9987(2015)03-0033-08
10.13808/j.cnki.issn1674-9987.2015.03.009
项 目:四川省科技支撑计划项目资助项目 (2014GZ0084)
林志明(1982-),男,工程师,硕士,2007年毕业于沈阳工业大学电力电子与电力传动专业,主要从事风力发电机组控制技术的研究工作。

