基于Baum-Welch算法HMM模型的孤词算法研究
陈军霞,刘紫玉
(河北科技大学经济管理学院,河北石家庄 050018)
基于Baum-Welch算法HMM模型的孤词算法研究
陈军霞,刘紫玉
(河北科技大学经济管理学院,河北石家庄 050018)
介绍了隐Markov模型原理,它是用来描述含有未知参数的Markov过程,是描述随机过程统计特性的概率模型。在此基础上,设计了基于HMM模型的孤词检测实验,通过优化实验模型,采用Baum-Welch算法解决HMM模型的训练问题,找到HMM模型估计参数λ值,这在数学角度上等价于其他线性预测系数。此实验在减少不必要的HMM训练的同时,降低了算法复杂程度。为了测试Baum-Welch算法的有效性,进行了数据仿真实验,结果表明该算法是有效的。
算法理论;Baum-Welch算法;隐Markov模型;随机过程
1 HMM模型介绍
隐Markov模型(Hidden Markov Models,HMM)是一种描述随机过程统计特性的概率模型,用来描述一个含有未知参数的Markov过程,在实际应用中,可用参数表示模型中的各种变量,其难点是从可观察的参数中确定该过程的隐含,再利用这些参数作进一步分析。作为研究语音信号的统计模型,它已经被广泛应用到语音处理的很多领域中,其理论基础是由BAUM[1-3]等在20世纪70年代建立起来的,随后由于JEDRUZEK[4]等对HMM应用的推广,使得该模型得到了传播和发展,成为信号处理的一个重要方向,现已成功地用于语音识别、行为识别、文字识别以及故障诊断等领域。近年来,HMM在生物信息科学、故障诊断等领域也开始得到应用。
1.1 HMM的基本思想
研究分析事物的发展状态,可以基于事物对象现在的状态对其将来的状态进行预测,而不需要考虑其过去的状态。由此,研究人员建立模型,提出了Markov链,即找到随机变量序列,序列中将来的随机变量与过去的随机变量无关,它有条件地依赖于当前的随机变量。在实际应用过程中,所研究的事件对象要比Markov链模型所描述的更为复杂,由于观察的事件与其状态不能够对应,致使不能直接观察到事件状态[5-6]。通过研究人员的努力与实践,在Markov链的基础上逐渐形成发展起来了HMM。HMM是描述离散时间数据样本的强有力统计工具,可以更好地表示网络数据,它由一系列可相互转移的有限状态集合组成,虽然状态转移不可见,但通过采取观测向量序列特性的方法能够间接地观测到状态,因为每个观测向量都是通过某些概率密度分布表现为各种状态,并且是由一个具有相应概率密度分布的状态序列产生的[7-9]。HMM是一个双重随机过程,是不确定的、随机的、有限状态集合,是不可观测的和可观测的2个随机过程的组合,是具有一定状态数的隐Markov链和显示随机函数集,如图1所示。

图1 HMM的组成Fig.1 Composition of the HMM
Markov链模型描述的是状态之间的转移,用转移概率对其进行描述。另一随机过程描述的则是状态与观察序列间的统计对应关系,用观察值概率对其进行描述,状态转移过程是没有办法观察到的,其结果只能观测到观察值,通过随机过程去描述状态的存在及其特性[10]。
1.2 Markov链
通过建立模型,Markov链状态和时间参数,在本研究中都可认为是离散的Markov过程。从数学上,给出如下定义:在状态空间(u1,u2,…,ui,…,uN)中,随机过程Xn在m+k时刻所处的状态概率为qm+k,Xn此时的状态只与它在m时刻的状态概率qm有关,而与m时刻以前它所处的状态无关,
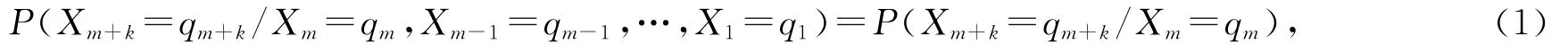
其中q1,q2,…,qm,qm+k∈(u1,u2,…,ui,…,uN),称Xn为Markov链,式(1)表示的性质称为无后效性,并且有:
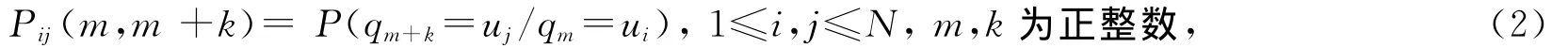
式(2)为k步转移概率,转移概率与状态及时刻m有关。当Pij(m,m+k)与m无关时,Markov链具有平稳的转移概率,则称这个Markov链为齐次Markov链,此时有:

在语音处理应用中,为了简化问题,Markov链就是齐次Markov链。当k=1时,称Pij(1)为一步转移概率,简称为转移概率,记为aij,所有转移概率aij可以构成一个概率转移矩阵A,即

由于k步转移概率Pij(k)可由转移概率aij通过C-K方程得到,因此,描述Markov链的最重要的参数是概率转移矩阵A。
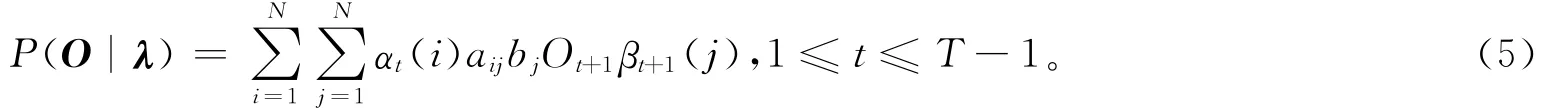
在给定的训练序列数有限的情况下,无法找到最佳的方法来计算估计参数λ值,但可以应用Baum-Welch算法,采用最大似然估计方法,利用其递归思想[11-12],使P(O/λ)局部最大,最后得到模型参数λ=(π,A,B)。
定义ξt(i,j)为给定训练序列O=(o1,o2,…,oi,…,oN)和模型λ=(π,A,B)时,在时刻t时Markov链处于ui状态和在时刻t+1时为uj状态的概率,即ξt(i,j)=P(O,qt=ui,qt+1=uj/λ)可以推出ξt(i,j)=[αt(i)aijbjOt+1βt+1(j)]/P(O/λ)。
那么在时刻t时Markov链处于ui状态的概率为,因此,
1.3 HMM描述
HMM由2个部分组成,一个是Markov链,由π,A描述,产生输出为状态序列,π表示初始状态概率分布,π=(π1,π2,…,πi,…,πN),其中πi=P(q1=ui),1≤i≤N,显然有0≤πi≤1,∑πi=1;A表示状态转移概率矩阵,A=(aij)N×N,其中aij=P(qm+k=uj/qm=ui),1≤i,j≤N,N是模型中Markov链状态总数,A中的元素aij表示从状态i转移到状态j的转移概率,且有∑aij=1。另一个是随机过程,产生的输出为观察值概率矩阵,由B描述,B=(bjk)N×M,其中bjk=P(Ot=vk/qt=uj),1≤j≤N,1≤k≤M,M为离散观察值可能取的符号总数。B中的元素bjk表示t时刻观察值vk在状态j的概率,且有∑bij=1。进而,HMM表示为λ=(π,A,B)。在模型中的3个要素中,要素π决定产生观察的HMM初始状态,其重要性最小,B直接与观察有关,影响最大,对于不同的被测对象,HMM的参数是不相同的,每一被测对象都可以用一个HMM模型λ=(π,A,B)表示。
只有解决了以下几个问题,才能有效地将HMM模型用于被测对象的检测中[10]。
1)对于给定的观察序列O=(o1,o2,…,oi,…,oN),调整模型λ=(π,A,B)中的各个要素,使观察序列O=(o1,o2,…,oi,…,oN)出现的概率P(O/λ)能够取得最大值。这相当于研究人员对原始数据分析,进行模型参数的优化估计,完成被测对象模型参数的训练过程,通过训练,为被测对象建立最佳模型。
2)给定观察序列O=(o1,o2,…,oi,…,oN),如何确定合理的状态序列,使之能最佳地产生观察序列O。
3)在给定的观察序列O=(o1,o2,…,oi,…,oN)和模型λ=(π,A,B)时,如何计算被测对象出现的概率P(O/λ),这相当于研究人员判断已知观察序列O=(o1,o2,…,oi,…,oN)由模型λ=(π,A,B)产生的可能性。通过与每一对象对应的模型λ=(π,A,B)计算出现概率P(O/λ),取概率最大的模型所对应的研究对象作为识别结果。
1.4 Baum-Welch算法介绍
Baum-Welch算法解决的是HMM训练问题,其结果是要找到HMM估计参数λ值,即给定一个观察值序列O=(o1,o2,…,oi,…,oN)和一个HMM模型λ=(π,A,B),如何调整参数λ值,使得观察值输出的概率P(O/λ)最大。表示从ui状态转移出去的次数的期望值,而表示从ui状态转移到uj状态次数的期望值。由此,导出Baum-Welch算法中重估公式:
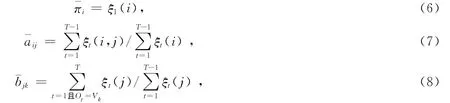
那么,求取HMM参数模型λ=(π,A,B)的过程可描述如下:根据给定的观察值序列(训练观察序列)O=(o1,o2,…,oi,…,oN)和选取的初始模型λ=(π,A,B),由式(6)—式(8)可求得一组新参数,亦即得到了一个新的模型¯λ=(¯π,¯A,¯B)。通过训练,证明此模型中,P(O/¯λ)>P(O/λ),即在表示观察值序列O=(o1,o2,…,oi,…,oN)方面,所得¯λ比λ更好,逐步改进模型λ=(π,A,B)中的参数设置,不断重复此优化过程,直到出现概率收敛,使得值达到最大,此时的¯λ即为所求模型。
2 HMM的训练实验
针对孤立词的识别进行HMM的训练,对于给定的N个词,对其进行语音测试,以识别它是哪个词,其实质就是对向量序列O(训练观察序列)的N分类问题。通过递推方法计算已知模型输出O=(o1,o2,…,oi,…,oN)及λ=(π,A,B)时产生输出序列的概率P(O/λ),用Baum-Welch算法,基于最大似然准则对模型参数λ=(π,A,B)进行修正,最估参数的求解表示为。用Viterbi算法输出序列的最佳状态转移序列X,即以X的最大条件后验概率为准则,其识别系统如图2所示。
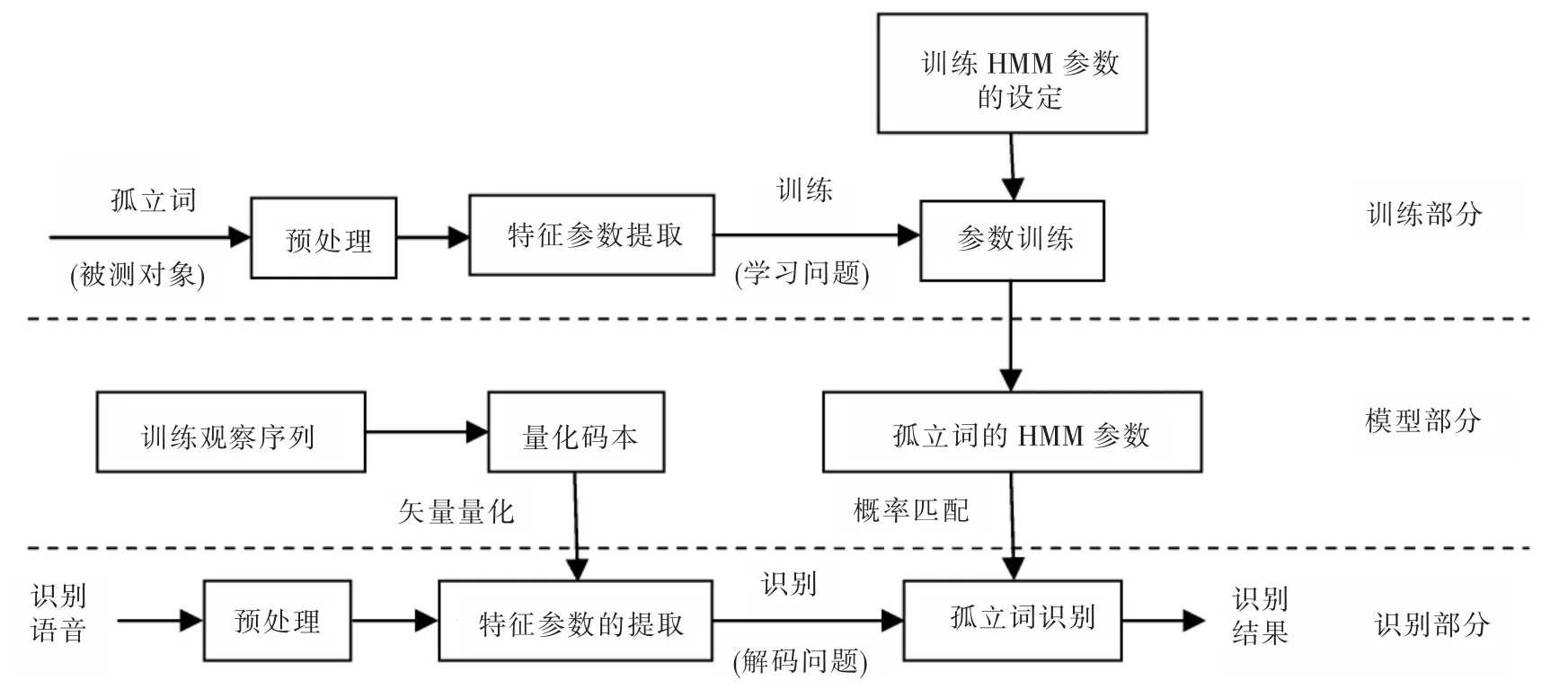
图2 孤立词识别系统Fig.2 Recognition system of isolated word
2.1 基本思想
为每一个词创建一个HMM,初始化参数。通过训练,调整模型参数;识别时,对每一个模型Mi,寻找其概率最大的状态路径(解码问题),M为离散观察值所取的符号总数。计算其概率P(O/λ)值。对所有训练模型结果,若概率P(O/λ)最大,则识别结果为第n个词。
2.2 确认系统设计
根据被测对象性质,本研究模型所构造的HMM确认系统框图如图3所示。
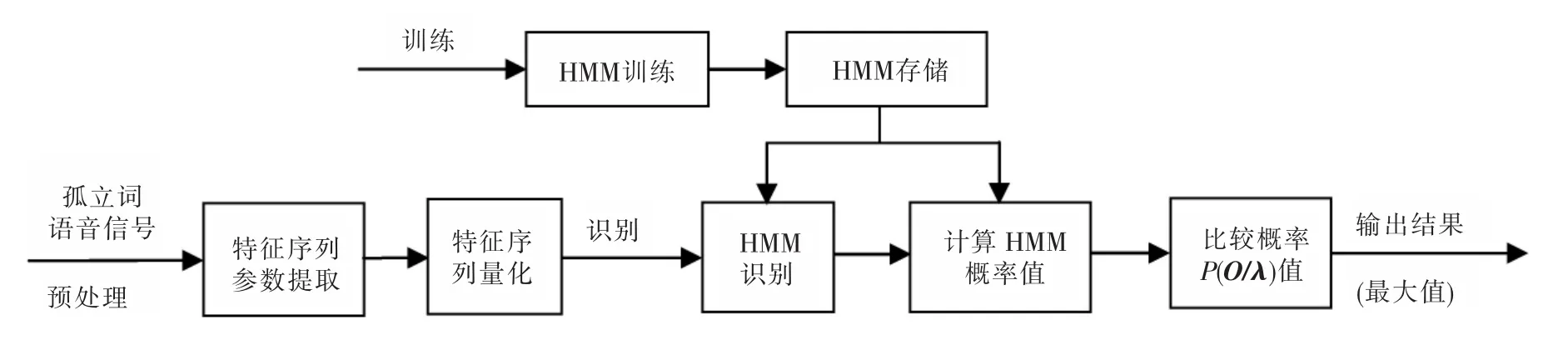
图3 HMM确认系统框图Fig.3 Confirmed the system block diagram of HMM
2.3 具体实现
1)模型选择原则 选择连续的HMM;结构一般选择从左向右(没有跨越);状态数一般为3~7个,通过反复实验选定最优;输出概率一般用混合高斯,高斯分量越多越精确,但越多计算量越大;一般采用有起点和终点状态的模型;模型的关键在于输出概率(混合高斯),状态转移概率相对来说不是很重要[13-15]。
2)输入数据(对应HMM各状态的输出) 每个词的语音按帧长30ms,帧移10ms分帧;每帧内提取MFCC特征(12维)能量;相邻帧之间求一阶、二阶差分;得到39维特征向量;所以,每个孤立词在系统内的表示是一个长度为T的39维的向量序列;
3)模型训练 首先进行参数初始化,进行随机/自设定/初始估计操作;接下来进行参数训练,应用Baum-Welch算法,每个孤立的模型只用其对应的语音训练。
4)语音识别 对于给定的特征向量训练O=(o1,o2,…,oi,…,oN),对每个HMM模型,寻找输出O=(o1,o2,…,oi,…,oN)的概率最大的状态路径,计算相应的概率P(O/λ)进行比较,概率最大的模型对应的词即为识别结果。
5)主要功能模块代码的实现

2.4 训练结果
根据本实验设计,使用数据集由30条长度为200的序列组成,由2个模型产生,见表1和表2。
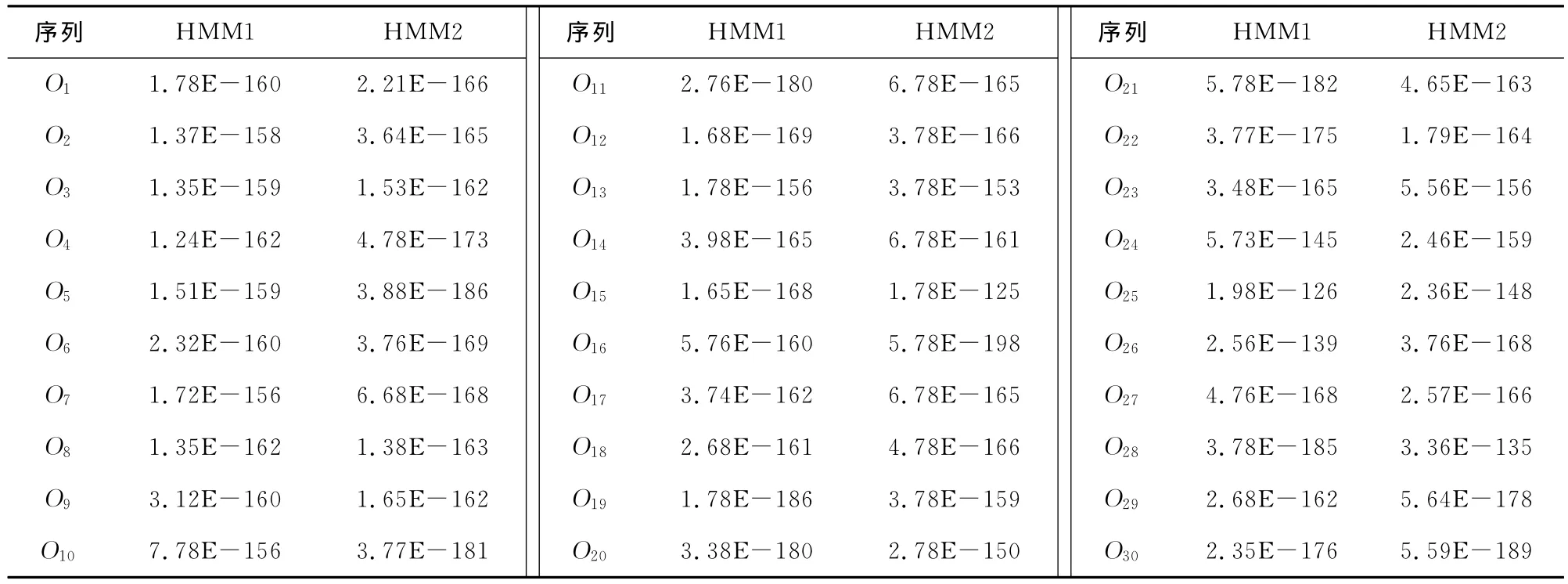
表1 30条序列分别在HMM1和HMM2模型中概率的例子Tab.1 Probability of 30sequences in HMM1and in HMM2
根据仿真实验结果,可知隐马尔可夫模型比基线模型获得了更好的识别结果,这得益于前者更有效地描述了被测对象相关性,说明训练序列O设计合理,更有效地找到了模型λ值,这在数学角度上完全等价于其他线性预测系数。
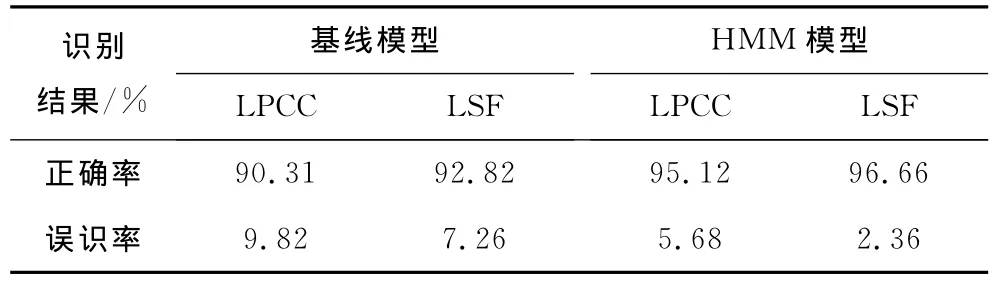
表2 实验所选模型与基线模型识别结果比较Tab.2 Comparison of identification result of selected model and the baseline model
3 结 语
将隐Markov模型概念及建立相应的隐Markov模型用于语音识别,理论分析和实验结果表明:使用HMM模型识别孤立词语音过程中,从检测机理上分析,音元状态转移概率A是逐帧变化的;转移概率A是根据词音发音时音元分布和实测统计的检测规律构建而成的;仿真结果证实,HMM算法对于孤立词检测效果高于基线模型。
[1] BAUM L,PETRIE E.Statistical inference for probabilistic function of finite state Markov chains[J].The Annals of Mathematical Statistics,1966,37(6):1554-1563.
[2] BAUM L E,EGON J A.An Inequality with applications to statistical estimation for probabilistic functions of a Markov process and to a model for ecology[J].Bull Amer Meteorol Soc,1967,32:360-363.
[3] BAUM L E,PETRIE T,SOULES G,et al.A maximization technique occurring in the statistical analysis of probabilistic functions of Markov processes[J].Ann Math Stat,1970,56:164-171.
[4] JEDRUZEK J.Speech recognition[J].Alcatel Telecommunications Review,2003,22:129-134.
[5] 蔡莲红.现代语音技术基础与应用[M].北京:清华大学出版社,2003.CAI Lianhong.The Foundation of Modern Speech Technology and Application[M].Beijing:Tsinghua University Press,2003.
[6] YOSHIZAWA S,MIYANAGA Y.A highspeed HMM VLSI module with block parallel processing[J].Electronics and Communications in Japan,PartⅢ:Fundamental Electronic Science,2004,87(5):12-23.
[7] 姚立月.基于HMM模型的说话人识别系统的研究[D].天津:天津大学,2006.YAO Liyue.The Research of Speaker Recognition System Based on HMM Model[D].Tianjin:Tianjin University,2006.
[8] 李秀珍.语音识别算法及应用技术研究[D].重庆:重庆大学,2010.LI Xiuzhen.Research on Speech Recognition Algorithm and Application[D].Chongqing:Chongqing University,2010.
[9] 张路.一种HMM的学习算法[D].成都:西南交通大学,2010.ZHANG Lu.A HMM Study Algotithm[D].Chengdu:Southwest Jiaotong University,2010.
[10]郑东亮,达飞鹏.一种求解最短枝切长度问题的学习算法[J].模式识别与人工智能,2011,24(5):645-650.DENG Dongliang,DA Feipeng.A learning algorithm for shortest branch cut length problem[J].Pattern Recognition and Artificial Intelligence,2011,24(5):645-650.
[11]高荣芳.一种基于可配置层级结构的导航树生成策略[J].西安石油大学学报(自然科学版),2012,27(5):95-98.GAO Rongfang.A navigation tree generation strategy based on configured hierarchy structure[J].Journal of Xi’an Shiyou University(Natural Science Edition),2012,27(5):95-98.
[12]谯倩,毛燕琴,沈苏彬.嵌入式Web访问控制系统的设计与实现[J].计算机技术与发展,2011,21(8):228-232.QIAO Qian,MAO Yanqin,SHEN Subin.Design and redlization embedded Web access control system[J].Computer Technology and Development,2011,21(8):228-232.
[13]于国庆,靳蕊,李永伟.均值分组块补零P码直捕算法原理及实现[J].河北科技大学学报,2014,35(2):172-178.YU Guoqing,JIN Rui,LI Yongwei.Principle and implement of P-code divect acquisition based on averge block zero padding[J].Journal of Hebei University of Science and Technology,2014,35(2):172-178.
[14]贺恩泽.一种面向服务体系架构的跨域单点登录系统的设计与实现[D].北京:北京邮电大学,2012.HE Enze.The Design and Implementation of a Single Sign-on Scheme for Cross Domain Web Applications Based on SOA[D].Beijing:Beijing University of Post Telecommunication,2012.
[15]周彦萍,马艳东.基于CP-ABE访问控制系统的设计与实现[J].计算机技术与发展,2014,24(2):145-149.ZHOU Yanping,MA Yandong.Design and implementation for access control system based on CP-ABE[J].Computer Technology and Development,2014,24(2):145-149.
Study on solitary word based on HMM model and Baum-Welch algorithm
CHEN Junxia,LIU Ziyu
(School of Economics and Management,Hebei University of Science and Technology,Shijiazhuang,Hebei 050018,China)
This paper introduces the principle of Hidden Markov Model,which is used to describe the Markov process with unknown parameters,is a probability model to describe the statistical properties of the random process.On this basis,designed a solitary word detection experiment based on HMM model,by optimizing the experimental model,Using Baum-Welch algorithm for training the problem of solving the HMM model,HMM model to estimate the parameters of theλvalue is found,in this view of mathematics equivalent to other linear prediction coefficient.This experiment in reducing unnecessary HMM training at the same time,reduced the algorithm complexity.In order to test the effectiveness of the Baum-Welch algorithm,The simulation of experimental data,the results show that the algorithm is effective.
theory of algorithm;Baum-Welch algorithm;hidden Markov model;stochastic process
TP391.42
A
1008-1542(2015)01-0052-06
10.7535/hbkd.2015yx01011
2014-09-12;
2014-10-28;责任编辑:李 穆
河北省自然科学基金(F2012208018);河北省高等学校科学技术研究重点项目(ZD2014027)
陈军霞(1973—),女,河北石家庄人,副教授,硕士,主要从事管理信息系统方面的研究。
E-mail:chenjunxia1234@163.com
陈军霞,刘紫玉.基于Baum-Welch算法HMM模型的孤词算法研究[J].河北科技大学学报,2015,36(1):52-57.
CHEN Junxia,LIU Ziyu.Study on solitary word based on HMM model and Baum-Welch algorithm[J].Journal of Hebei University of Science and Technology,2015,36(1):52-57.

