Combined effect of Reynolds and Grashof numbers on mixed convection in a lid-driven T-shaped cavity filled with water-Al2O3nanofluid*

MOJUMDER Satyajit， SAHA Sourav， SAHA Sumon， MAMUN M. A. H.

Department of Mechanical Engineering， Bangladesh University of Engineering and Technology， Dhaka-1000，Bangladesh， E-mail: sjit018@gmail.com

Combined effect of Reynolds and Grashof numbers on mixed convection in a lid-driven T-shaped cavity filled with water-Al2O3nanofluid*

MOJUMDER Satyajit， SAHA Sourav， SAHA Sumon， MAMUN M. A. H.

Department of Mechanical Engineering， Bangladesh University of Engineering and Technology， Dhaka-1000，Bangladesh， E-mail: sjit018@gmail.com

2015，27（5）:782-794

Lid-driven mixed convection has been given immense importance due to its wide range of applications. A T-shaped cavity is introduced and pertinent parameters controlling mixed convection phenomenon are analyzed in this paper. Water-Al2O3nanofluid is considered inside the cavity to augment heat transfer rate. Galerkin weighted residual method of finite element analysis is applied for the numerical simulations. Numerical solution is obtained for different solid volume fractions of nanofluid （φ=0-0.15），Grashof numbers（Gr=0.1-5000）and Reynolds numbers （Re=0.31-1000）in laminar flow regime. Special attention is given on the analysis of flow at the pure mixed convection regime. It is found that Grashof， Reynolds and Richardson numbers along with solid volume fraction of nanofluid have significant effect on heat transfer characteristics inside the cavity. Results are presented using streamline and isotherm contours along with related variation of average Nusselt numbers of the heated wall and average fluid temperature inside the cavity.

mixed convection， nanofluid， lid-driven， T-shaped， Richardson number， finite element

Introduction

Studies of mixed convection heat transfer have been given keen attention since the end of last century due to its application in modern science and technology. At present， owing to its vast application field in electronics cooling technology， chemical process technology， glass and ceramic industries， solar thermal technology， space heating， food processing industries and so on， mixed convection heat transfer is gaining attention around the world.

Mixed convection problems can be broadly classified into two basic categories. Those are either forced flow inside an open cavity or lid-driven closed cavity problems. The lid-driven problems can be classified into different categories based on the movement of cavity walls such as any or both side walls moving， upper or bottom wall moving， periodic wall movement etc.. Some basic parameters that control the mixed convection for lid-driven cavity are Reynolds number，Prandtl number， Grashof number， Richardson number，geometric shape， inclination angle and so on. Moallemi and Jang［1］investigated the effect of Prandtl and Reynolds numbers for laminar mixed convection in a top wall moving， bottom heated lid-driven square cavity. They found that when Reynolds and Grashof numbers were kept constant， increment of Prandtl number enhanced the heat transfer rate. Prasad and Koseff［2］experimented a lid-driven square cavity flow with constant heat flux boundary condition for a wide range of Richardson numbers. They described a correlation for Nusselt and Stanton numbers suitable for design application. Aydin and Yang［3］studied the mixed convection in a square cavity having side wall moving and local heat source at the bottom wall. They reported that with the increment of Richardson numbers， three regimes （forced， mixed and natural） of convection were found for different heat source lengths. Oztop and Dagtekin［4］analyzed mixed convection for lid-driven square cavity with both sidewalls moving. They conducted the study for three different configu-rations based on the direction of moving walls. They concluded that for Ri＞1， whereRiis the Richardson number， heat transfer enhancement was possible. Ji et al.［5］studied transient mixed convection in a square cavity where the upper wall was moving and reported that for steady state， when Ri＜1， the temperature range remained uniform and for increment ofRi， the flow evolved over the diffusion time scale. Sivakumar et al.［6］observed the effect of heated sidewall in a square cavity， which had its upper wall moving. They found that the middle and top configurations had enhanced heat transfer rate. Mamun et al.［7］studied mixed convection in a trapezoidal cavity whose top wall was moving and reported that increment ofRi augmented the heat transfer rate.

Cavity shape is a pertinent parameter of the analyses of mixed convection. Different shapes of cavity have been studied already for lid-driven problems. Among those geometries， square， rectangular， triangular， trapezoidal shapes are very common. T-shaped cavity， however， is very practical from engineering point of view. However， this shape of cavity has not been throughly studied so far. Mansour et al.［8］studied natural convection in a T-shaped cavity filled with nanofluid having localized heat source and they came to the conclusion that the narrower part of T-shaped cavity augmented the heat transfer rate. Solid volume fraction of the nanofluid also plays a positive role on heat transfer. Rouijaa and Alami［9］also studied natural convection in an inclined T-shaped cavity and reported that increase of inclination angle was not favorable for heat transfer augmentation. Similar type of works considering radiation effect inside a T-shape cavity was investigated by Amraqui et al.［10］. They concluded that increment of Rayleigh number enhanced heat transfer rate. Recently， Kasaeipoor et al.［11］carried out a numerical study on the mixed convection of Cuwater nanofluid in a vented T-shaped cavity in the presence of a uniform magnetic field. Therefore， T-shaped cavity has a huge potential for contributing to the enhancement of heat transfer rate. However，mixed convection analysis in a lid-driven T-shaped cavity has not been studied until now.

Nanofluid has been introduced in recent years to increase the heat transfer rate. Basically， nano-sized（1 nm-100 nm） particles suspended in conventional base fluid such as air， water modify the thermo-physical properties of the conventional fluid that often results in augmentation of heat transfer. For this reason，metal， metal-oxide， carbonaceous materials are being used extensively as nanoparticles in the base fluid. Use of nanofluid in lid-driven mixed convection has been considered to augment the heat transfer rate by many researchers. Mansour et al.［12］studied mixed convection in a square cavity filled with nanofluid and subjected to constant heat flux at the bottom wall. They reported that increase of Reynolds and Rayleigh numbers enhanced the heat transfer rate. Talebi et al.［13］also analyzed mixed convection flow in a square cavity whose side walls were heated and top wall was lid-driven and the cavity was filled with Cu-water nanofluid. They stated that increase of Reynolds number decreased the solid concentration and augmented the heat transfer. Muthtamilselvana et al.［14］investigated heat transfer in a lid-driven rectangular cavity for Cu-water nanofluid and they concluded that aspect ratio and solid volume fraction influenced the heat transfer. Further related works on lid-driven cavity filled with nanofluid were described by Nemati et al.［15］，Muthtamilselvan and Doh［16］， Abu-Nada and Chamkha［17］， Karimipour et al.［18］.

The present study aims to investigate lid-driven mixed convection in a T-shaped cavity filled with Al2O3-water nanofluid. According to the best knowledge of the authors， lid-driven T-shaped cavity has not been analyzed extensively with the constraints and conditions presented in this paper， although this is a very practical type of problem. The numerical simulation has been carried out for wide range of Reynolds and Grashof numbers and solid volume fractions. Emphasis has been given to understand the pure mixed convection phenomenon at Ri=1， which is yet to be investigated.

Fig.1 Schematic diagram of the T-shaped cavity

1. Mathematical formulation

1.1 Physical description

The details of the geometry considered in the present investigation are shown in Fig.1. It is a T-shaped cavity simulated in two-dimensional as shown in Fig.1（a）， however， the three-dimensional model of the present problem is also illustrated in Fig.1（b）. The top wall of the cavity is lid-driven and moving at a constant velocity u0in x-direction while the bottom and the other sidewalls are kept stationary. The length of the top wall and the height of the cavity are remaining fixed at the same length，L. The upper moving wall is maintained at low temperature，T=Tc. The bottom wall is heated and kept at high temperature，Th（＞Tc）. Other sidewalls of the cavity are thermally insulated. The gravity is acting in the negative direction of they-axis. Water-Al2O3nanofluid is considered as the working fluid for the present investigation. The radiation effect and viscous dissipation along with internal heat generation have been neglected.

1.2 Mathematical modelling

The working fluid is assumed to be incompressible Newtonian fluid. Two-dimensional continuity，Navier-Stokes and energy equations have been applied to model the problem. The flow is assumed to be steady and laminar with constant fluid properties except density variation of the nanofluid which has been considered according to the Boussinesq approximation. A thermal equilibrium exists between the base fluid and the nanoparticles. From the assumptions stated above， the continuity， momentum and energy equations for the present problem can be written as:

The density of the nanofluid，ρnf， depends on the solid volume fraction，φand can be expressed as

where ρfand ρsare the densities of the base fluid and the nanoparticles respectively. Here the subscript“s” represents the properties of nanoparticles and“f” represents those for base fluid. The subscript“nf” is used to denote the property of the nanofluid. To model the effective viscosity of the nanofluid，µnf， Brinkman model［19］is used and can be expressed as follows

where µfis the dynamic viscosity of the base fluid. Thermal expansion coefficient（β）can be expressed as

The effective thermal diffusivity of the nanofluid，αnfis

The effective thermal conductivity of the nanofluid，knfis approximated using Maxwell-Garnetts model［20］as

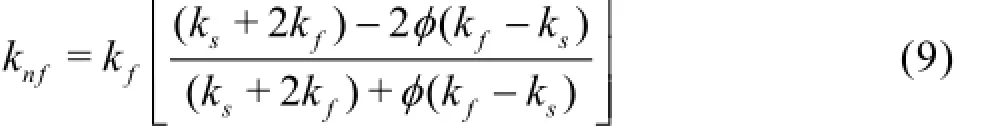
where kfand ksare the thermal conductivity of the base fluid and nanoparticles respectively. The heat capacitance of the nanofluid can be given by

It is convenient to solve the governing equations in non-dimensional forms and hence following scales are used to get the non-dimensional governing equations:

The non-dimensional governing parameters considered in the present simulation are as follows:

whereRe，Pr，GrandRi are Reynolds， Prandtl，Grashof and Richardson numbers respectively. Richardson number is an important parameter to study the mixed convection phenomenon. When Ri=1， it signifies the case as a pure mixed convection. If Richardson number is low（Ri＜0.1）the viscous force dominates the flow， and the flow can be assumed to be assisted by forced convection. However，when Richardson number has higher values（Ri＞10）the buoyant force dominates the viscous force， and the fluid flows as a result of natural convection.

Using the above mentioned scale， the non-dimensional forms of continuity， momentum and energy Eqs.（1）-（4） can be expressed as:

The boundary conditions shown in Fig.1（a） can be written in non-dimensional forms and are presented in Table 1.

Table 1 Present boundary conditions in non-dimensional form

Important non-dimensional parameters such as average fluid temperature inside the cavity can be calculated using the following expression

whereA is the non-dimensional area of the cavity and given by A=（1-b/L+ab/L2）. The characteristics of heat transfer can be evaluated using average Nusselt number of the heated bottom wall and is expressed by the following relation

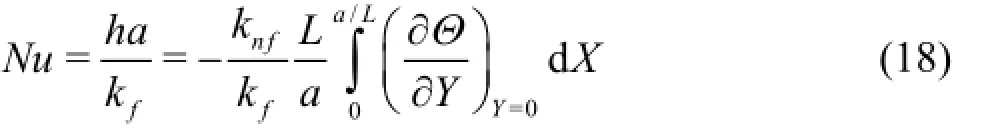
1.3 Properties of nanofluid

Improved thermo-physical properties of the nanofluid are the main reasons for its use to augment heat transfer rate. Different types of nanofluid have been studied by previous researchers and it was reported that nanofluid enhances the heat transfer rate significantly. Among the available nanofluids， Cu-water，Al2O3-water， TiO2-water are being used extensively from the economical point of view， whereas we have selected Al2O3-water nanofluid for the present simulation. The thermo-physical properties of the base fluid（water） and the nanoparticles （Al2O3） are presented in Table 2.

Table 2 Thermo-physical properties of water and Al2O3［21］

Fig.2 Finite element mesh generation within the computational domain of the T-shaped cavity

2. Numerical method and validation

2.1 Numerical procedure

Galerkin weighted residual scheme of finite element analysis has been applied for the numerical solution. The entire domain of the cavity is discretized using triangular mesh elements as shown in Fig.2. Finer meshes near the wall boundary are applied to get the more accurate result. Non-dimensional governing Eqs.（13）-（16） are transformed into the system of nonlinear algebraic equations， which are then solved by iteration technique. A converging criterion has been set for， where γ is the general dependent variable.

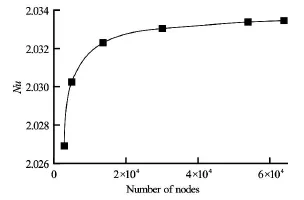
Fig.3 Variation of average Nusselt number with different mesh size for Gr =103，Ri =1and φ=0

2.2 Grid independent test

A grid independent test has been performed to check the numerical accuracy of the solution. Figure 3 shows the results of the grid independent test. The test is performed for Gr =103and Ri =1by considering only the base fluid （water） inside the cavity（φ=0）. From Fig.3， it is evident that for coarse mesh （5 000 nodes）， average Nusselt number is low and with the refinement of mesh size （increasing node number）Nu increases significantly. However， for about 30 000 nodes， average Nusselt number becomes almost constant. Further increment of nodes does not initiate a significant change of Nu . Therefore， a node size of 30 000 is selected as the optimum mesh size for all cases of the present numerical simulations.

2.3 Code validation

The present code is validated with the previous work of Abu-Nada and Chamkha［21］. Validation check is performed through the observation of streamline，isotherm and average Nusselt number plots. The detailed results are presented in Figs.4 and 5. Both streamline and isotherm contours show good agreement with the previous work for Ri =1and solid volume fraction φ=0 and 0.1. Comparison of the average Nusselt number is carried out for differentRiat φ= 0 （base fluid） and φ=0.1（nanofluid）. It is evident from Fig.5 that the present code is completely reliable to carry out further complicated simulation within reasonable numerical accuracy.

Fig.4 Code validation of the present simulation via with Abu-Nada and Chamkha［21］for Ri =1，φ=0（base fluid）and φ=0.1（nanofluid）. Solid line and dotted line represents the present code

Fig.5 Comparison of average Nusselt number for different Ri at solid volume fraction φ=0（base fluid） and φ=0.1（Cnhaanmo fklhu ia d［2）1］with the results of Abu-Nada and

3. Results and discussion

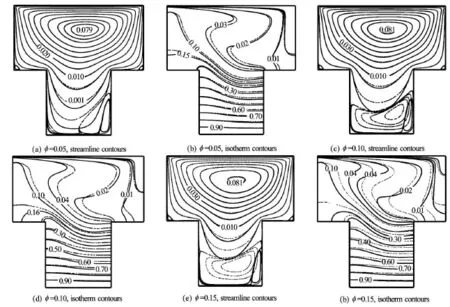
Fig.6 Comparison of streamline and isotherm contours with the plain fluid（φ=0）at Re =31.6，Gr =103and Ri=1. The solid line in each figure represents the data for plain fluid（φ=0）whereas the dashed line represents nanofluid with different φ

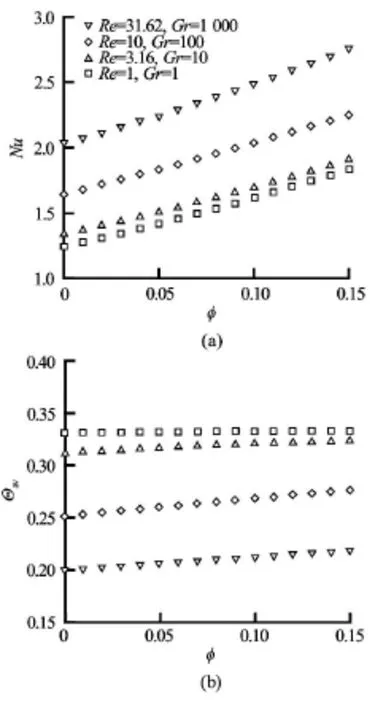
Fig.7 Variation of （a） average Nusselt number of the heated bottom wall and （b） average temperature of fluid inside the cavity with solid volume fraction for Ri=1 inside a lid-driven T-shaped cavity filled with water-

The primary objective of the current investigation is to study different features of mixed convection Al2O3nanofluid. Consequently， the implications of varying Reynolds and Grashof numbers and solid volume fraction of nanoparticles in the fluid on the mixed convection heat transfer are emphasized. To highlight changes in flow pattern and evolution of heat transfer regimes， streamline and isotherm contours are plotted and compared for different computational conditions. Three cases of solid volume fractions （φ= 0.035， 0.1 and 0.15） are analyzed atRi =1and Gr= 10 and comparison is made for streamline and isotherm contours with the base fluid（φ=0）. Influence of varying Reynolds numbers is studied by altering the value of Reynolds numbers （Re=10， 31.62 and 100）atφ=0 and 0.15 respectively while keeping Gr=103. Effect of different Grashof numbers is studied by varying its value （Gr = 250， 2 500 and 5 000） atRe=50. Besides， the combined effect of Reynolds and Grashof numbers at fixed Richardson number（Ri=1）on the flow and thermal fields of the cavity under pure mixed convection condition is investigated extensively. Average Nusselt number of the heated wall and average temperature of the flow field inside the cavity have been plo tted against solid volume fra ction， Reyno lds，GrashofandRichardsonnumberstounderstandthecontribution of these parameters on mixed convection heat transfer inside the cavity.

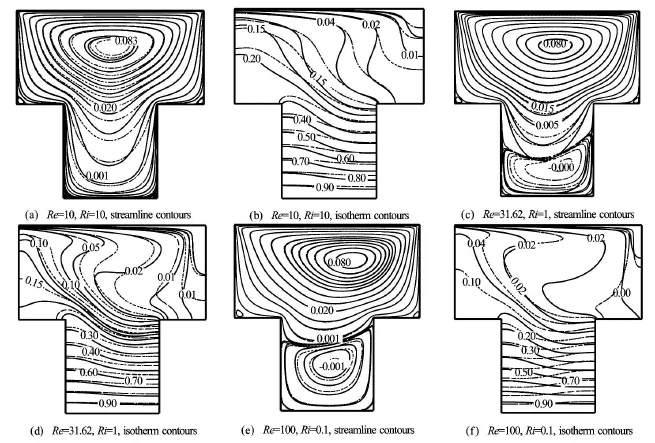
Fig.8 Comparison of streamline and isotherm contours at Gr =103. The solid line in each figure represents the data for plain fluid（φ=0）whereas the dashed line represents nanofluid with φ=0.15

3.1 Effect of solid volume fraction of nanofluid

Figure 6 portrays a comparison in the streamline and isotherm fields between the plain fluid（φ=0）and the nanofluid with different amounts of nanoparticles. The relative percentages of nanoparticles in the fluid are taken to be φ=0.05， 0.1 and 0.15 and comparisons of flow and thermal fields are performed every time with the case ofφ=0（base fluid） to intensify the difference due to the presence of the nanoparticles. In order to observe the sole effect of solidvolume fraction， the governing parameters such as Reynolds and Grashof numbers and consequently Richardson number are kept constant atRe =31.6，Gr =103and Ri≈1. It is expected that due to the introduction of nanoparticles in the base fluid （water），the resulting thermal properties of the nanofluid improve significantly and as a result， both streamline and isotherm fields undergo drastic change in compared with the results of the plain fluid. As shown in Figs.6（a）， 6（c） and 6（e）， a clockwise vortex is induced adjacent to the moving lid at the top which is basically tangential to the direction of the moving lid. Here the dominating mechanism is the forced convection arising due to the moving lid. Now the effect of thermal buoyant force is observed near the bottom wall of the cavity. Within the cavity， the lighter and warmer fluid after taking heat from the hot bottom wall goes upward and due to the presence of the lid-driven vortex，a counter rotating cell is formed just below the main vortex. Thus， the two vortices of different strength and rotating direction inside the cavity actually represent the characteristics of mixed convection phenomenon. By observing streamline plots for φ=0， it can be noticed that the lid-driven vortex is the dominant vortex consuming almost the entire area of the cavity. On the other hand， the thermal buoyancy induced vortex appears to be weaker in strength and barely exists near the right side of the bottom wall. As the percentage of solid volume fraction of nanoparticles in the base fluid is increased， there is an improvement of thermal properties （e.g.， increased thermal conductivity） of the nanofluid. This phenomenon is depicted in Fig.6 for φ＞0where the thermal buoyancy induced vortex near the bottom hot wall is strengthened and becomes larger with increasing solid volume fraction of the nanoparticles. However， the lid-driven vortex is still the dominating one and has comparatively higher strength.

While observing the isotherm fields， a noticeable difference in the contour distribution of temperature between the nanofluid and the plain fluid is found on the upper portion of the cavity， which is totally opposite for the streamline plots. For both plain and nano-fluids， the isotherms having higher values （Θ≥0.5）are almost parallel and clustered near the bottom wall region. This type of distribution is a characteristic of high temperature gradient in that heating zone. The effect of lid-driven vortex in the upper portion of the cavity takes the leading role to improve the mixing of the heated fluid and thus， the isotherm patterns become distorted in the upper region. In fact， the heavily distorted thermal regions imply the characteristics of forced convection which is significantly affected by the change of solid-volume fraction of the nanoparticles. For higher value ofφ， the distortion in the isotherm contours takes place intensively around the wider part of the cavity in compared with the plain fluid. However， isotherm contours for nanofluid（φ≥0.05） seem to have shifted a bit upward in the narrowwer part of the T-shaped cavity. This indicates rapid heat dispersion near the bottom heated wall at higher solid volume fraction.

Figures 7（a） and 7（b） exhibit the influence of solid volume fraction of nanoparticles on average Nusselt number of the heated bottom wall and average fluid temperature inside the cavity. The computational conditions， in order to observe the sole effect ofφat the pure mixed convection situation， are fixed in such a way that the Richardson number remains always unity. Four different sets of simulation are performed by varying both Reynolds and Grashof numbers while keeping Ri=1. The first noticeable point in Fig.7（a）is that the average Nusselt number increases with increasing Reynolds and Grashof numbers. It is expected to have better heat transfer for higher value of ReandGr. Moreover， higher percentages of solid particles in the base fluid improve the convection heat transfer and the results show linear variation ofNu andφ. On the other hand， Fig.7（b） reveals that the average fluid temperature shows consistent result with the increase ofReandGr . However， the effect ofφ on the average fluid temperature depends entirely on the choice ofReandGr . At lowReand Gr（Re= Gr=Ri =1）， the rate of change of Θavwithφis so low that it seems to be constant. Further increase of ReandGrcauses the average fluid temperature sensitive with the change of solid volume fraction. In fact，Θavincreases slightly for increasingφand it creates a bit of dilemma since increasing mixing fluid temperature and average Nusselt number may only exist simultaneously for the change of solid volume fraction of nanoparticles.

Fig.9 Variation of （a） average Nusselt number of the heated bottom wall and （b） average temperature of fluid inside the cavity with Reynolds and Richardson numbers for Gr=103

3.2 Effect of Reynolds numbers

Figure 8 shows a comparative study of streamline and isotherm contours between the cases φ=0 and 0.15 for different Reynolds numbers （Re=10， 31.62，100） whileGr=103. At constant Grashof number， the corresponding Richardson numbers are 10， 1.0 and 0.1 respectively for the above Reynolds numbers. It is a well-known fact that Reynolds number signifies the relative importance between inertia and viscous forces in a flow field. Higher value of Reynolds number represents the domination of inertia force in a flow field over the viscous force. For low Reynolds number（Re=10）， the lid-driven vortex seems to be dominating the entire cavity for plain fluid. With the introduction of nanofluid at moderate Reynolds number（Re=31.62）， another vortex initially appears near the heated bottom wall and then gradually becomes a secondary thermal buoyancy induced vortex for higher Re which is rotating in counter-clockwise direction. For plain fluid， the secondary vortex only exists at higher Reynolds number indicating the flow is dominated by the forced convection induced by the moving lid. As the value of Reynolds number is increased， the lid-driven vortex becomes stronger and occupies only the top part of the cavity. Due to higher strength of thelid-driven vortex at highRe ， it needs to move rapidly for better mixing and as a result， only spreads over the wider portion of the cavity. The resulting vacant space at the narrower part of the cavity is then filled by the secondary buoyancy induced vortex for both plain and nanofluids. Although the counter-clockwise buoyancy induced vortex becomes larger at lower Richardson number （consequently higherRe ）， the flow is still governed by the forced convection due to higher strength of the lid-driven vortex. It is to mention that the difference of the streamline patterns between the plain and the nanofluids can be noticed at low to moderate Reynolds number with the presence of thermal buoyancy induced vortex.

Fig.10 Comparison of streamline and isotherm contours at Re =50. The solid line in each figure represents the data for plain fluid（φ=0）whereas the dashed line represents nanofluid with φ=0.15

From the isotherm plots in Figs.8（b）， 8（d） and 8（f）， it is found that the contour lines are generally adjacent parallel to the bottom wall of the cavity and distorted completely around the top wider region. The parallel and clustered distribution of the isotherm contours signifies a steep temperature gradient near the bottom wall. When the Reynolds number increases，the area inside the cavity covering low temperature contours spreads gradually due to strong forced convection induced by the moving lid. It is interesting to observe that the isotherm contours near the bottom wall for the nanofluid tends to distort sharply in compared with the plain fluid at high Reynolds number. Hence， even for low Richardson number， the nanofluid with improved thermal properties is influenced by the dominating forced flow of the lid-driven vortex.

The effect of Reynolds number on the performance of the plain fluid and the nanofluid （φ=0.15）is further evaluated from the distribution of average Nusselt number and average fluid temperature of the cavity. The results are shown in Figs.9（a） and 9（b） respectively as a separate function of both Reynolds and Richardson numbers at constant Grashof number（Gr =103）. At this value ofGr and lowRe， the flow is expected to be dominated by laminar free convection even when the Richardson number becomes very high. The variation ofNuwith increasingReor decreasingRifollows the similar trend for both the plain and nanofluids although the nanofluid exhibits better thermal performance compared to the plain fluid. Moreover， due to the improved for forced convection effect with increasingRe or decreasingRi，the average Nusselt number increases gradually and reaches to a maximum atRe≈725and Ri≈0.002 for nanofluid， and at Re≈675and Ri≈0.0022for plain fluid. Further increase of Reynolds numbers （or decrease of Richardson numbers） does not improve heat transfer rate sinceNubegins to drop from the maximum point. Over the computational range ofRe ，the forced convection plays a leading role due to the negligible effect of laminar free convection at Gr=103. The average fluid temperature of the cavity is depicted in Fig.9（b） and follows the expected trend almost linearly decreasing with increasing Reynolds numbers and decreasing Richardson numbers. Besides，Θavfor nanofluid is always higher than for plain fluid which is consistent with the findings explained in Section 3.1.

3.3 Effect of Grashof numbers

The influence of Grashof number at constant Reynolds number on the flow and thermal fields are now investigated for both plain and nanofluids（φ= 0.15）. Streamline and isotherm contours are plotted in Fig.10 for Gr=250， 2 500 and 5 000， and the correspondingRi =0.1， 1 and 2 while keeping Re=50. At low Gr and Re， the streamline pattern （see Fig.10（a））consists of a large lid-driven clockwise vortex in the wider part of T-shaped cavity and a smaller vortex in the narrower part with counter-clockwise rotation. For Gr =250and Ri=0.1， flow pattern is usual with a large vortex in the extended part of T-shaped cavity and a smaller vortex in the bottom part of the cavity. There is no difference in the streamline contours observed for both plain and nanofluid atGr =250and Re=50. When the Grashof number increases， the smaller vortex at the bottom region diminishes and the larger vortex covers the entire cavity with an increased strength. However， this evolution of streamlines does not occur similarly for both plain and nanofluids. In case of nanofluid（φ=0.15）， due to the improved thermal properties， the smaller buoyancy induced vortex retains its presence at moderate Grashof and Richardson numbers （see Fig.10（b） forGr=2500 and Ri=1）. When the Grashof number increases， the lid-driven vortex expands towards the narrower region of the cavity and thus induces free convection heat transfer due to the increased temperature gradient. The difference of the streamline patterns between the plain and the nanofluids appears dominantly at higherGr andRi .

The isotherm patterns for both plain and nanofluids are quite similar for low Grashof and Richardson numbers （see Fig.10（b））. The contour lines are parallel and clustered near the bottom wall whereas distorted isotherms are distributed in the extended upper portion of T-shaped cavity. With the increase of Grashof and Richardson numbers， the intensity of free convection heat transfer becomes higher and thus the isotherms in both parts of the cavity undergo noticeable distortion for both plain and nanofluids. This distortion in the isotherm contours indicates strong convection at higher Grashof and Richardson numbers. However， change in isotherm pattern for nanofluid with high Grashof and Richardson numbers is not as significant as it is for plain fluid. As a result， at higher value of Grashof and Richardson numbers， isotherms show less distortion for nanofluid.

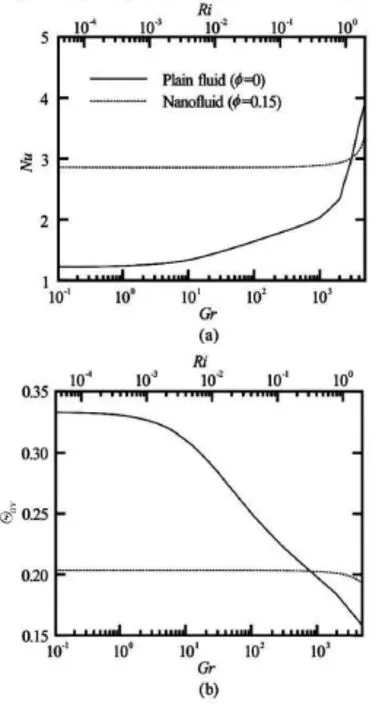
Fig.11 Variation of （a） average Nusselt number of the heated bottom wall and （b） average temperature of fluid inside the cavity with Grashof and Richardson numbers for Re=50

Variations of average Nusselt number at the heated bottom wall and average fluid temperature with the change of Grashof numbers for Re=50are illustrated in Fig.11 for both plain and nanofluids. Here we can observe some interesting features with the presence of nanoparticles. In fact， there is no effect of Grashof number onNu and Θavfor nanofluid（φ=0.15）until Ri=1. It can be concluded with the present findings that within the forced convection regime， the influence ofGrfor nanofluid is almost negligible and the variations ofNuand Θavremain constant for Gr≤3000（Ri≤1）. On the other hand，for plain fluid， the average Nusselt number and average fluid temperature are almost constant forGr≤10. Further increase of Grashof number shows a gradual increment ofNuand decrement of Θavas expected. It is also exp ected that the pre sen ce of nano fluid will enhancetheheattransferrateincomparedwiththeplain fluid. However， when Ri＞1and Gr＞3000，the plain fluid shows higherNuin compared with the nanofluid. Interestingly， at this low Reynolds number（Re=50）， the plain fluid， although having higher average fluid temperature than the nanofluid， displays a decreasing trend ofΘavwith the change of Grashof number which becomes lower than the nanofluid at Gr≥103.

Fig.12 Comparison of streamline and isotherm contours at Ri =1. The solid line in each figure represents the data for plain fluid（φ=0）whereas the dashed line represents nanofluid with φ=0.15

3.4 Combined effect of Reynolds and Grashof numbers at pure mixed convection

Figure 12 now compares the performance of the plain fluid and the nanofluid （φ=0.15）via streamline and isotherm contours by considering the combined effect of Grashof and Reynolds numbers while the Richardson number is kept constant. In fact， the analysis is performed at pure mixed convection regime by fixingRi =1. Three sets of Grashof numbers，Gr= 10， 100 and 3 100， and the corresponding value of Reynolds numbers are Re=3.16， 10 and 55.67 respectively atRi=1are chosen to examine the evolution of streamline and isotherm patterns for both plain and nanofluids. From Figs.12（a）， 12（c） and 12（e）， it is observed that there is a common trend of the evolution of streamlines with increasing Grashof and Reynolds numbers. For low Grashof and Reynolds numbers，there are two distinct vortices inside the cavity having opposite sense of rotation. In the wider part of the T-shaped cavity， the clockwise rotating vortex induced by the moving lid is dominant while the narrower part of the cavity is occupied with a weak buoyancy induced vortex. Interestingly， there is no difference between the plain and the nanofluids in the streamline contours at lowGrandRe . With the increase ofGr andRe ， the lid-driven vortex expands towards the narrower part of the cavity and grows larger. On the other hand， vortex near the heated bottom wall becomes weaker and shrinks in size and strength. In case of nanofluid， this evolution process occurs at a slower rate whereas the leading lid-driven vortex for the plain fluid dominates the whole cavity at higherGrand Re . For nanofluid at Gr =3100and Re=55.67， the buoyancy induced vortex moves near the right part of the bottom wall and thus indicates the influence of nanoparticles on the flow field.

There is always a noticeable difference in the isotherm contours between the plain fluid and the nanofluid atRi=1. Isotherms with higher magnitude are distributed parallel to the bottom wall at low to moderateGr. However， when Gr =3100and Re=55.67，due to strong convective effect， the parallel distribution of isotherm contours breaks up and is distorted throughout the cavity. In fact， the evolution of temperature field shows significant difference between the plain fluid and the nanofluid.

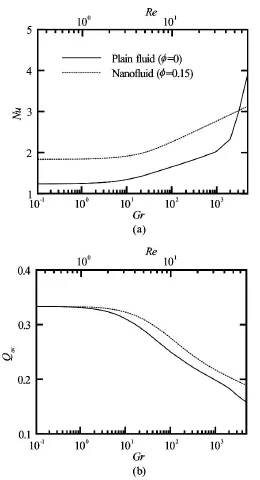
Fig.13 Variation of （a） average Nusselt number of the heated bottom wall and （b） average temperature of fluid inside the cavity with Grashof and Reynolds numbers for Ri=1

Figure 13（a） exhibits the distribution of average Nusselt number as a function of Grashof and Reynolds numbers at Ri=1. The performance of nanofluid is always higher than the plain fluid. However， with the increase of Grashof number， as explained in Section 3.3， the plain fluid starts enhancing heat transfer rate over the nanofluid fromGr≥3100. This reveals the fact that by introducing higher Grashof number at constant Richardson number（Ri= 1）， heat transfer enhancement takes place rapidly without the necessity of adding any nanoparticles in the base fluid. The average fluid temperature inside the cavity is shown in Fig.13（b） with the variation of bothGrandRe. At Ri=1， both plain and nanofluids exhibit similar behavior with reducing the average fluid temperature for increasing Grashof and Reynolds numbers. However， the rate of reduction is very low forand， and with the increase ofGrandRe，for both plain and nanofluids decreases sharply. Moreover， the average temperature of the flow field for nanofluid always remains higher than that of plain fluid.

4. Conclusions

Steady laminar mixed convection heat transfer in a T-shaped cavity has been analyzed numerically in this paper. Natural convection is introduced by an isothermally heated bottom wall while lid-motion at the cold top wall induced forced convection regime of heat transfer. A comparison of performance between the plain fluid and the nanofluid is performed under the aforementioned flow scenario. The following conclusions can be made here.

（1） Higher solid volume fraction of nanoparticles in the fluid yields a better convection heat transfer scenario.

（2） With increment of Reynolds numbers， the flow field inside the cavity undergoes a drastic change.

（3） Higher Reynolds number strengthens overall flow inside the cavity. It also produces a stronger and larger buoyancy-driven vortex.

（4） High value of Grashof number works in favor of better heat transfer. Increased Grashof number results in higher Nusselt number value.

（5） At high Grashof number and Ri=1， elevated heat transfer rate is obtainable even using plain fluid. Higher values of Grashof number weaken the buoyancy-driven vortex near the heated bottom wall.

（6） At constant Grashof number， Richardson number has more influence on flow inside the cavity than Reynolds number. Thermal buoyancy effect is generally stronger in nanofluid under the same condition.

Acknowledgement

The authors gratefully acknowledge the support provided by the Department of Mechanical Engineering， Bangladesh University of Engineering and Technology （BUET）， Dhaka， Bangladesh during this research work.

References

［1］ MOALLEMI M. K.， JANG K. S. Prandtl number effects on laminar mixed convection heat transfer in a liddriven cavity［J］. International Journal of Heat Mass Transfer， 1992， 35（8）: 1881-1892.

［2］ PRASAD A. K.， KOSEFF J. R. Combined forced and natural convection heat transfer in a deep lid-driven cavity flow［J］. International Journal of Heat Fluid Flow， 1996， 17（5）: 460-467.

［3］ AYDIN O.， YANG W. Mixed convection in cavities with a locally heated lower wall and moving sidewalls［J］. Numerical Heat Transfer Applications， 2000，37（7）: 695-710.

［4］ OZTOP H. F.， DAGTEKIN I. Mixed convection in twosided lid-driven differentially heated square cavity［J］. International Journal of Heat and Mass Transfer，2004， 47（8）: 1761-1769.

［5］ JI T. H.， KIM S. Y. and HYUN J. M. Transient mixed convection in an enclosure driven by a sliding lid［J］.Heat and mass transfer， 2007， 43（7）: 629-638.

［6］ SIVAKUMAR V.， SIVASANKARAN S. PRAKASH P. et al. Effect of heating location and size on mixed convection in lid-driven cavities［J］. Computers and Mathematics with Applications， 2010， 59（9）: 3053-3065.

［7］ MAMUN M. A. H.， TANIM T. R. and RAHMAN M. M. et al. Mixed convection analysis in trapezoidal cavity with a moving lid［J］. International Journal of Mechanical and Materials Engineering， 2010， 5（1）: 18-28.

［8］ MANSOUR M. A.， BAKIER A. Y. and BAKIER M. A. Y. Natural convection of the localized heat sources of T-shaped nanofluid-filled enclosures［J］. American Journal of Engineering Research， 2013， 2（7）: 49-61.

［9］ ROUIJAA H.， ALAMI M. E. Natural convection in an inclined T-shaped cavity［J］. Fluid Dynamics and Materials Processing， 2011， 7（1）: 57-70.

［10］ AMRAQUI S.， MEZRHAB A. and ABID C. Computation of coupled surface radiation and natural convection in an inclined T form cavity［J］. Energy Conversion and Management， 2011， 52（2）: 1166-1174.

［11］ KASAEIPOOR A.， GHASEMI B. and AMINOSSADATI S. Convection of Cu-water nanofluid in a vented T-shaped cavity in the presence of magnetic field［J］. International Journal of Thermal Sciences， 2015， 94: 50-60.

［12］ MANSOUR M. A.， MOHAMED R. A. ABD-ELAZIZ M. et al. Numerical simulation of mixed convection flows in a square lid-driven cavity partially heated from below using nanofluid［J］. International Communications in Heat and Mass Transfer， 2010， 37（10）: 1504-1512.

［13］ TALEBI F.， MAHMOUDI A. H. and SHAHI M. Numerical study of mixed convection flows in a square liddriven cavity utilizing nanofluid［J］. International Communications in Heat and Mass Transfer， 2010，37（10）: 79-90.

［14］ MUTHTAMILSELVANA M.， KANDASWAMY P. and LEE J. Heat transfer enhancement of copper-water nanofluids in a lid-driven enclosure［J］. Communications in Nonlinear Science and Numerical Simulation，2010， 15（6）: 1501-1510.

［15］ NEMATI H.， FARHADI M. and SEDIGHI K. et al. Lattice Boltzmann simulation of nanofluid in lid-driven cavity［J］. International Communications in Heat and Mass Transfer， 2010， 37（10）: 1528-1534.

［16］ MUTHTAMILSELVAN M.， DOH D. H. Mixed convection of heat generating nanofluid in a lid-driven cavity with uniform and non-uniform heating of bottom wall［J］. Applied Mathematical Modelling， 2014，38（13）: 3164-3174.

［17］ ABU-NADA E.， CHAMKHA A. J. Mixed convection flow of a nanofluid in a lid-driven cavity with a wavy wall［J］. International Communications in Heat and Mass Transfer， 2014， 57: 36-47.

［18］ KARIMIPOUR A.， ESFE M. H. and SAFAEI M. R. et al. Mixed convection of copperwater nanofluid in a shallow inclined lid driven cavity using the lattice Boltzmann method［J］. Physica A: Statistical Mechanics and Its Applications， 2014， 402: 150-168.

［19］ BRINKMAN H. C. The viscosity of concentrated suspensions and solution［J］. The Journal of Chemical Physics， 1952， 20（4）: 571-581.

［20］ MAXWELL-GARNETT J. Colours in metal glasses and in metallic films［J］. Philosophical Transactions of the Royal Society of London. Series A， Containing Papers of a Mathematical or Physical Character，1904， 203: 385-420.

［21］ ABU-NADA E.， CHAMKHA A. J. Mixed convection flow in a lid-driven inclined square enclosure filled with a nanofluid［J］. European Journal of Mechanics B/ Fluids， 2010， 29（6） : 472-482.

10.1016/S1001-6058（15）60540-6

（November 21， 2014， Revised July 16， 2015）

* Biography: MOJUMDER Satyajit （1993-）， Male，Undergraduate Student

SAHA Sumon，E-mail: sumonsaha@me.buet.ac.bd