北黄海庄河养殖海域污染物运动轨迹数值模拟
郝子宁,张明亮,张云鹏,乔 洋
(大连海洋大学 海洋科技与环境学院,辽宁 大连116023)
大连到庄河海域位于黄海北部,其中包括老虎滩、大连湾和庄河部分海域。这部分海区为不规则的半日潮,其中M2分潮占主要成分,并且潮流呈往复流性质。该海区的海洋资源条件优越,海洋养殖生物种类繁多,资源量大。近年来,由于近海养殖业的迅速发展,庄河近海海域滩涂贝类、对虾、人工流放增殖和浮筏养殖基地逐年增多,养殖水域的投饵、施肥、药物使用等对近海域的水质影响日益显著,其近海养殖活动成了这片海域污染的主要来源之一。
随着计算机和数值模拟技术的发展,采用海洋环境动力数学模型来研究海域的水动力和水环境状况等问题受到越来越多的关注。如Moon基于ROMS(Regional Ocean Modeling System)的一个拉格朗日粒子追踪实验模拟中国东北部黄海和日本海的巨型水母分布[1]。Mitaras应用ROMS海洋模式,耦合拉格朗日粒子追踪方法来研究海洋水体中物质的输运结构和路径,并对污染物在海洋中的运动状态进行预测[2]。Bilgili等基于二维模型耦合拉格朗日模块研究粒子在美国新罕布什尔州河口的时空分布情况[3]。汪守东等采用水动力学模型POM(Princeton Ocean Model)模式模拟与预报了渤海海峡突发性溢油事故,采用Lagrangian追踪法模拟油膜的输移扩散[4]。张越美等基于ECOM模型(Estuary Coastal Ocean Model)模拟渤海湾三维潮流场的时空分布特性[5],王振华、龚煌及褚芹芹等[6-8]基于ECOMSED三维水动力模型,结合拉格朗日粒子追踪技术,模拟长江口排污口、大连湾水域和胶州湾粒子的运动轨迹及污染物输运过程。
近年来,结合有限差分的离散方法与有限元的网格易曲性等优点的有限体积法被广泛应用,如Chen、Wei及Ge 等[9-11]采用三维海洋模型研究美国东南沿岸Satilla河、中国长江口和中国南海海水运动特性,讨论了网格的分辨率对其模拟精度的影响,王平等[12]基于三维潮流模型耦合拉格朗日粒子追踪模块模拟大连湾内的水动力特性和特征粒子的运动轨迹。这些模型是基于非结构化网格的FVCOM海洋模式,可以更好地拟合不规则的岸线,在垂向坐标计算上使用sigma坐标变换,在垂向上使用相同的层数,使其在模拟不同水深、地形变化不剧烈时有很大优势,并且在模拟浅水区域也会得到较好的结果。目前,采用环境动力学模型来研究北黄海庄河养殖海域水动力和水体污染物运动轨迹的较少,已有的研究是基于深度平均二维模型,这些模型对岸线的拟合精度及计算结果都不十分理想,并且该海域的水深变化显著,因此应更多地应用三维模型来研究该海域养殖活动对其水质的影响。
本文采用FVCOM海洋模型,耦合拉格朗日粒子追踪方法,对北黄海庄河养殖海域进行详细的数值计算,基于拉格拉日拉格朗日粒子追踪模块模拟庄河养殖海域污染物的迁移规律,从潮流的角度分析该海域水体粒子的运动过程。
1 数学模型
潮流模型为基于有限体积法的FVCOM数值模式,该模型结合了有限元体积法和有限差分法,便于离散计算海洋原始方程组,使其在理论和数值计算方面有很大优势。同时该模型兼顾拟合边界和局部加密的优点,潮汐的移动边界用干湿判断法处理。采用改进的Mellor-Yamada 2.5 阶紊流闭合模型及Smagorinsky湍流闭合法,使垂直和水平混合模型在物理和数学上闭合,不规则的底部边界采用σ垂直变换来体现。
1.1 基本控制方程
控制方程采用σ坐标系下三维连续、动量方程[13-14]:


式中 t为时间;u,v,ω为x,y,σ方向的速度分量;D为水深;η为基准面到海表面距离。σ和z的关系式为σ=(z-η)/(H+η);Km为垂直涡旋粘性系数;ρ0为参考密度,ρ为海水密度;g为重力加速度;f为科氏参数;DFx,DFy和D(Fq2,Fq2l)为水平扩散项,AM,Ah分别为水平和垂向紊动粘性系数;q2和l分别是湍动能和湍动的宏观尺度;H为基准面到海底的距离。
Km由修正的Mellor-Yamada(2.5)湍流闭合模型计算,计算公式为:

式中 Ps和Pb分别为剪切和浮力引起的湍流动能产生项;ε为湍流动能耗散率;Kq为湍流动能垂向涡粘扩散系数;为近似壁面函数。
湍流动能混合长度方程由下列等式关系闭合:

Sm为稳定函数。根据Mellor和Yamada,Sm由下列方程组确定:

粒子轨迹运动方程可表达:

ω,w的关系:

1.2 边界条件
在σ坐标系下,海面σ=0,边界条件为:

在海底σ=-1,边界条件为:

式中τsx,τsy为海表面风应力;(u+v)为海底切应力。
陆地边界条件法向速度和通量为0,即vn=0。外海开边界给定水位,用干湿边界法处理开潮滩,注入海域的河流做源项处理。
2 庄河养殖海域的数值模拟
2.1 计算域与网格
海域水环境的演变过程主要受潮流的影响,也就是说,水体中的污染物是以潮流作为运动的载体,在海水往复运动的同时,其污染物会扩散输移至外海。庄河位于大连的东部,其海域有多个养殖区域,主要是底栖贝类生物。这类底栖贝类生物在养殖的过程中会产生、排泄一定的氮磷污染物,进一步造成海域水体营养盐富集,形成富营养化。鉴于庄河养殖海域独特的特点,选择该海域进行污染物的扩散输移研究。该海域的计算区域范围经度为121.5°~124.1°,纬度计算范围为38.4°~39.8°,包括老虎滩、大连湾、大窑湾和庄河部分海域。主要的汇入河流有5条,包括大洋河、沙河、碧流河、赞子河、登沙河,其入口给定流量边界条件。
图1为大连至庄河海域的平面网格示意图,其中大窑湾、小长山岛2个站点可以进行潮位验证,石城岛附近的一个站点进行潮流流速及流向验证。海域地形来自中国人民解放军海军司令部航海保证部出版发行的北黄海海图,利用SMS软件提取地形,并生成无结构化不规则三角形网格,水平方向采用可变分辨率策略,实现对近岸、海岛及海底地形陡峭区域进行局部网格加密,在近岸和海岛附近,网格分辨率较高,例如石城岛和小长山岛养殖海域附近,在外海开边界处及周边的网格较为稀疏,如图1所示。这样划分网格的目的在于精细网格能够较好地复演重点区域的真实流态,外海粗网格可以节省计算时间,提高计算效率。整个计算海域包括13469个三角形网格,垂向设为10个σ层,外模时间步长设定为1s。该海域的潮位开边界在计算域的下方,开边界潮位过程线通过M2,S2,K1和O14个分潮计算。

图1 计算域网格示意图
2.2 监测点的潮位对比
水动力模拟时间段选择在2011年8月份,从8月16日至8月31日,包括一个完整的大潮和小潮过程。
图2和图3为大窑湾和小长山岛潮位站模拟的潮位与实测数据的对比。由图可见,无论是在大潮还是小潮时间段,大窑湾和长山岛潮位的实测值和计算值吻合较好,误差在0.2~0.5m范围内,总的来说模拟的误差也在允许范围内。

图2 大窑湾计算潮位和实测值比较(2011-08-16~2011-08-31)
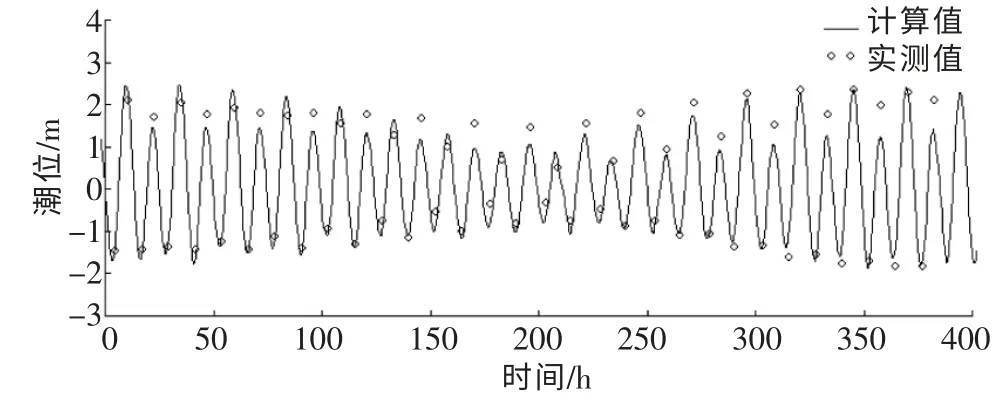
图3 小长山岛计算潮位和实测值比较(2011-08-16~2011-08-31)
图4~图5为不同站点模拟的流速、流向与实测数据的对比,可见,模拟结果能够反应实际水流的运动特征,潮流模拟的表层和底层的流向也基本一致,大潮时流速一般在0.3~0.6m/s之间,小潮时流速一般在0.1~0.3m/s之间。由于受海底地形影响,表层、底层流速差距为0.1m/s。

图4 大潮期表层、底层的流速和流向计算值和实测值比较
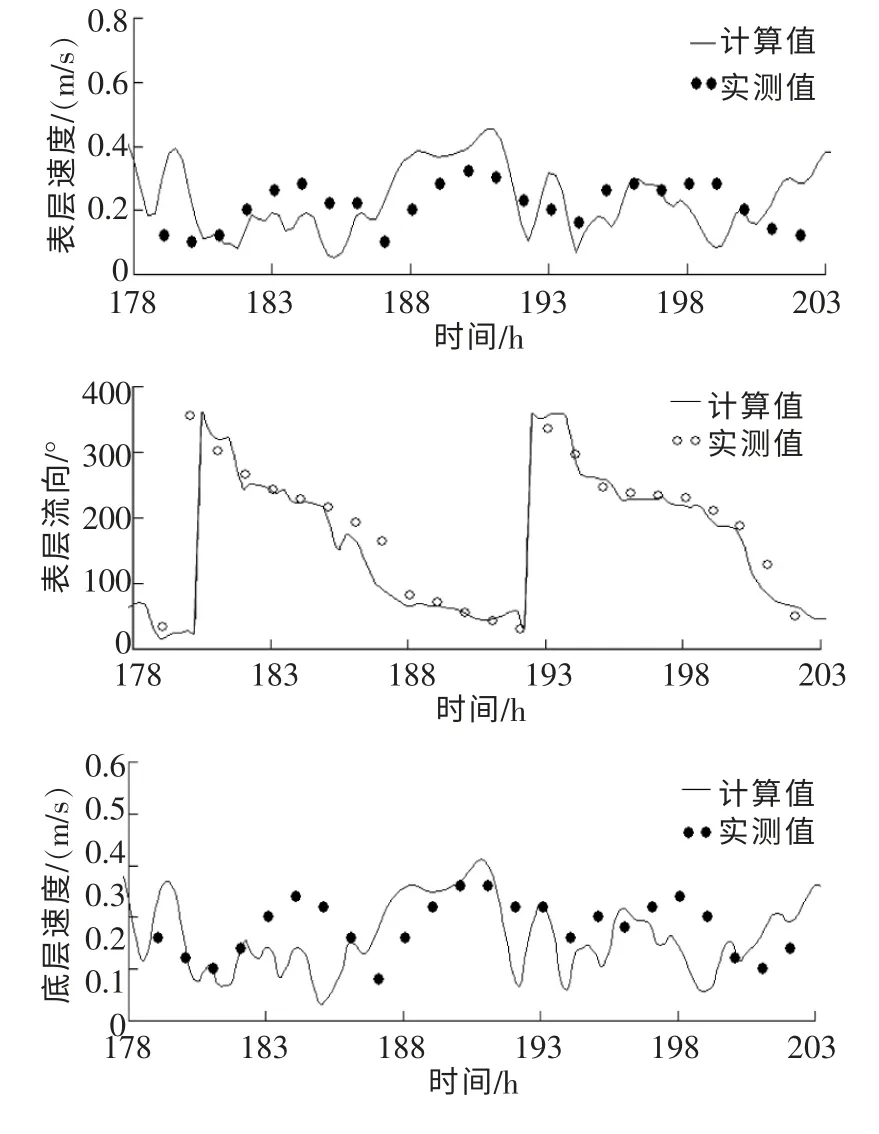

图5 小潮期表层、底层流速和流向计算值和实测值的比较
图6为石城岛海域周围模拟的某一落潮时刻流场,最大流速出现在岛屿间的水道附近,在岛屿附近发生绕流,在岛屿或岸边附近受地形影响流速明显变小,整个区域潮流还具有明显的往复特征。在黄海潮波的作用下,随着潮位涨落,局部海域会出现周期性的偏涡区变化。

图6 石城岛周围海域模拟的流场
2.3 模拟粒子运动轨迹
模拟海中投放群粒子具有明显的规律性,通过分析群粒子随水体发生迁移和扩散,可判断污染物在该区域内排放时对该水域整体水环境的影响。在石城岛附近的养殖区域选取两个投放点,通过拉格朗日法模拟群粒子的运动轨迹来研究污染物的运动规律。因模拟单个粒子的运动规律存在一定的随机性,为了更好地模拟污染物的运动轨迹,采用群粒子为研究对象,粒子群运移规律通过质心轨迹来反映。
质心坐标的计算公式为:

式中 x(t),y(t),z(t)为粒子群质心在某时刻的x,y,z轴的坐标,xi(t),yi(t),zi(t)单个粒子在某时刻的x,y,z轴坐标;n为模拟粒子总数。
粒子模拟时间段为2011年8月20日零时至2011年9月5日。2011年8月20日零时,向石城岛东侧和西侧2个养殖海域(1#和2#)的水体中分别每层投放100个粒子,10层共放置1000个粒子,Begin为粒子投放点,End为粒子在结束时的位置。
粒子的运动轨迹如图7所示,通过模拟群粒子的输移轨迹来研究污染物的运动规律,发现粒子的运动轨迹与释放的位置有关。1#投放点位于石城岛的东南侧,2#投放点位于石城岛的东北侧。由图7可以看出,通过15d追踪,在1#投放点投放的粒子群在前几天内随水流会做往复运动,一段时间后粒子群质心在潮流作用下向东南方向运动,流向外海,粒子净输移距离较长,大约60km。该投放点的粒子群受潮流影响较大,易向外扩散,不易发生滞留,能够快速扩散输移至外海,计算结果表明该区的水体比较活跃,水交换能力较强。在2#投放点,在涨落潮流的作用下,粒子以螺旋形式沿着海岸线来回往复运动,但总体向东侧偏移,主要是落潮流驱动作用,粒子输移的距离较短,大约20km,可以发现,该位置海域的水体交换较差,污染物扩散、输移能力较弱。同时也对石城岛南侧的部分海域进行了粒子模拟,其粒子运动朝向东南,一段时间后快速移向外海。

图7 石城岛周围海域投放粒子的运动轨迹
3 结语
北黄海海域附近岛屿众多,并且海岸线极不规则,FVCOM模型基于有限体积法和非结构化三角网格,其三角形网格能更好地拟合黄海北部海域的复杂不规则岸线和岛屿,同时有限体积法能保证每个网格单元的质量守恒,进而达到计算域整体质量守恒。计算结果表明:
(1)污染物多伴随落潮方向迁移,在靠近海岸方向迁移扩散较慢,岸边和岛屿附近的粒子滞留时间较长,所以在近岸水域大量的底栖贝类养殖将对岸边的水环境带来较大影响。
(2)石城岛西南侧海域的粒子净输移较长,该区的水体交换能力较好,而石城岛东北侧海域离岸较近,其粒子沿着岸线向东侧运动,其输移距离较短,该区域的污染物扩散输移能力较弱,离岸线较远的石城岛东侧养殖海域污染物的输移能力较强,远离海岸水域的贝类养殖水环境能够在潮流的作用下进行充分交换。
(3)各个投放点垂向上粒子运动差别不大,主要原因是水深较浅,对环境影响较小。
[1]Moon J H,Pang I C,Yang J Y.Behavior of the giant jellyfish Nemopilema nomurai in the East China Sea and East/Japan Sea during the summer of 2005:A numerical model approach using a particle-tracking experiment[J].Journal of Marine Systems,2010,80(1-2):101-114.
[2]Mitarai S,Siegel D A,Watson J R,et al.Quantifying connectivity in the coastal ocean with application to the Southern California Bight[J].Journal of Geophysical Research,2009,114,C10026:1-21.
[3]Bilgili A,Proehl J A,Lynch D R,et al.Estuary/ocean exchange and tidal mixing in Gulf of Maine Estuary:A Langrangian modeling study[J].Estuarine,Coastal and Self science,2005,65:607-624.
[4]汪守东,沈永明,郑永红.海上溢油迁移转化的双层数学模型[J].力学学报,2006(4):452-461.
[5]张越美,孙英兰.渤海湾三维变动边界潮流数值模拟[J].青岛海洋大学学报(自然科学版),2002(3):337-344.
[6]王振华,唐军,李春良,等.长江口污染物运动轨迹模拟[J].海洋环境科学,2012(1):1-5.
[7]龚煌,孙大鹏,孙志国.采用三维潮流模型分析人工岛对海湾污染物运动的影响 [J].水道港口,2013 (3):263-271.
[8]褚芹芹,李磊,李培良.胶州湾潮流场的示踪粒子数值模拟研究[J].中国海洋大学学报(自然科学版),2010(11):29-34.
[9]Chen C S,Liu H D,Beardsley R C.An unstructuredgrid,finite-volume,three-dimensional,primitive equations ocean model:application to coastal ocean and estuaries[J].Journal of Atmospheric and Oceanic Technology,2003,20:159-186.
[10]Wei J,Zhang D,Xue P.et al.Coupling of a regional atmospheric model (RegCM3)and a regional oceanic model(FVCOM)over the maritime continent [J].Clim Dyn,2014,43:1575-1594.
[11]Ge J Z,Guo W Y,Ding P X.Hydrodynamic influence of proposed excavated-in harbor in the Hengsha Shoal of the Yangtze Estuary Ⅰ:Numerical Model and Validations[J].Journal of East China Normal University (Natural Sc),2013,2013(4):79-90.
[12]王平,张宁川.大连湾保守污染物迁移三维模型及应用[J].海洋通报,2013(3):265-274.
[13]宋德海,鲍献文,张少峰,等.基于FVCOM的廉州湾及周边海域三维潮汐潮流数值模拟[J].海洋通报,2012(2):136-145.
[14]陈长胜.海洋生态系统动力学与模型[M].北京:高等教育出版社,2003.

