城际铁路连续梁拱桥铰座受力分析

冯 飞

(中铁工程设计咨询集团有限公司，北京 100055)

城际铁路连续梁拱桥铰座受力分析

冯 飞

(中铁工程设计咨询集团有限公司，北京 100055)

以国内某新建城际铁路连续梁拱桥铰座为例，对铰座部件进行了建立在接触理论上的受力分析，并建立Ansys有限元实体受力模型，进一步分析铰座竖转受力特征。结论表明：在最不利工况下铰座强度能够满足规范要求；有限元分析证实受力计算结果，工程实践证明采用接触理论开展同类型工程设计是可行的。

城际铁路；连续梁拱桥；铰座；接触理论；有限元分析

1 工程设计概况

为满足桥下通航要求，国内某城际轨道交通项目跨河大桥主桥采用(100+180+100) m预应力混凝土连续梁与钢管混凝土拱组合结构，该结构为目前国内同类型桥梁当中最大跨度。

拱肋采用钢管混凝土结构，计算跨度L=180 m，设计矢高f=36.0 m，矢跨比f/L=1/5，拱轴线采用二次抛物线，设计拱轴线方程：Y=(-1/225)X2+0.8X。拱肋于拱顶设置最大0.1 m预拱度，施工矢高f=36.1 m，施工拱轴线方程Y=-0.004 456 79X2+0.802 222X。

钢管混凝土拱桥常见的架设方法是斜拉悬臂法。对于拱梁组合桥先梁后拱法施工来说，一般采用支架法，但随着跨度增大矢高增高，受结构自身限制而不能采用支架法，这时可以采用转体法中的上提式竖转来完成[1]。施工顺序为先合龙混凝土连续梁，利用桥面作为搭设拱肋的拼装平台，利用塔架进行拱肋竖转，完成全桥合龙。

结合国内交通项目同类型结构设计成果[2，3]，为适应拱肋竖转要求，在拱肋与铰座间设置竖向转铰结构(图1)。该构造具有造型简单、施工难度低等优点。

图1 铰结构图示

铰座与连接铰均为钢结构，铰座与连接铰接触面进行机械加工。铰座由圆弧钢板、撑板、垫板等组成，材料为Q345qD钢材。圆弧钢板厚度20 mm，内径255 mm，圆心角135.58°；撑板厚20 mm、宽100 mm；平垫板厚20 mm，宽1 000 mm。连接铰由铰头、加劲板等组成，材料为Q345qD钢材。连接铰外径250 mm，厚度20 mm。拱座采用C60钢纤维混凝土。

2 拱肋竖转提升过程及铰座反力

主拱竖转过程中随着提升索张紧，铰座与连接铰产生接触反力，在拱肋的提升过程中，接触反力产生变化。反力分别经过铰座传递给拱座，经过连接铰传递给拱肋。提升过程中提升索力、拱肋自重、接触反力形成动态平衡状态，拱肋提升模型见图2。

图2 拱肋提升模型(半拱)及坐标系

为便于施工，拱肋采用不对称拼装方案，拱肋分为大半拱和小半拱，以大半拱为例进行受力分析，考虑拱肋自重及施工机具，计算大半拱侧自重379 t，。提升工艺采用连续提升，铰座受力见表1。

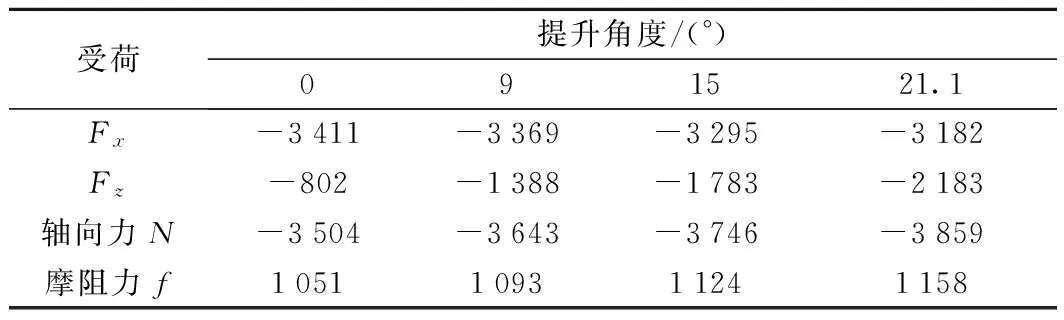
表1 铰座受力 kN

注：受压为负。

由表1可以看出，随着提升角度增大，拱脚轴力及摩擦力逐渐增大，提升角达到21.1°时为最大工况。横向设置限位或风缆，此处不纳入局部计算。

3 铰座受力分析

3.1 赫兹理论分析

接触问题研究很早就引起了人们的重视。早在1882年，H.R.赫兹研究了物体在相互接触的力作用下发生的弹性变形[4]。随着发展之后出现了一些非经典的数值解法[5]。经典赫兹理论研究两物体因受压相触后产生的局部应力和应变分布规律。在此基础上发展起来的接触力学理论假定：①接触区发生小变形；②接触面呈椭圆形；③相接触的物体可被看作是弹性半空间，接触面上作用分布的垂直压力。相关公式[6]如下

(1)

(2)

本项目为内接触，式中取负号；

式中α——接触面半宽，m；

ρ1、ρ2——连接铰、铰座曲率半径，m；

E1、E2——两接触体材料弹性模量，取2.1×108kPa；

μ1、μ2——两接触体材料泊松比，取0.3；

b——接触长度，m；

F——接触力，kN;

σHmax——最大接触应力，kPa。

在赫兹接触问题中，由于接触区附近的变形受周围介质的约束，因而各点处于三向应力状态，且接触应力的分布呈高度局部性，随离接触面距离的增加而迅速衰减。

实际工程中的有些接触问题接触面间存在摩擦时的滑动接触、滚动接触等。赫兹接触已应用在有些桥梁工程小部件设计中[7]。本项工程竖转铰提升过程中铰座存在附加滑动的摩擦接触，从满足工程应用的角度出发，结合接触理论进行分析。

3.2 应力计算

铰座圆弧钢板与连接铰之间可根据与轴线平行的圆柱凹面接触问题，按几何条件归为的点接触问题，施加荷载后，变为面接触。

(1)拱肋刚脱离胎架提升之前，索力、拱肋自重、接触反力形成平衡，系统满足赫兹接触假定。根据赫兹公式，接触压应力可按弹性力学求解，接触图示见图3。

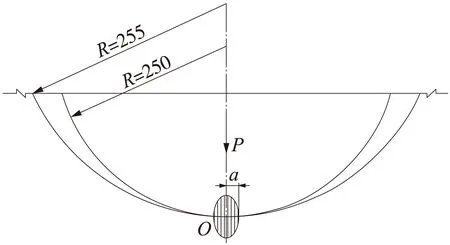
图3 接触应力内接触图示

由公式(2)，求得

σHmax=-111.1 MPa，本工程b=0.9 m。

(2)拱肋提升过程中，连接铰与铰座间产生了摩擦力，索力、拱肋自重、接触反力、摩擦力形成新平衡系统。围绕接触点O，以垂直和平行于合力的平面截取单元体，单元体为三向应力状态。摩阻力产生的切向应力按如下公式计算[8]

(3)

式中f——摩阻力，kN；

b——接触面长度，m；

δ——层状裂纹深度，m；取0.015。

求得τ=85.8 MPa。

根据计算结果，计算主应力[9]，得到：

σ1=12.1 MPa

σ2=-47.6 MPa，

σ3=-170.8 MPa。

以第四强度理论进行校核

161.5 MPa<[σ]=300 MPa[10]

说明在拱肋起吊最大工况下铰座受力满足要求。

3.3 有限元分析3.3.1 模型建立

针对铰座受力采用有限元程序Ansys建立模型。模型考虑铰座圆弧钢板及板后混凝土，两者共享界面。模型采用plane42实体板结构单元进行模拟。尺寸选取铰座长1 m，高0.3 m范围实体，划分共36 848个单元，18 798个节点，对所选实体除朝拱座向上方向一面的其他面进行了变形约束，施加提升最大高度时轴向力及摩阻力组合工况，有限元模型见图4。

图4 铰座有限元模型

3.3.2 计算结果

提升最大工况下铰座钢板主应力云图如图5～图7所示。

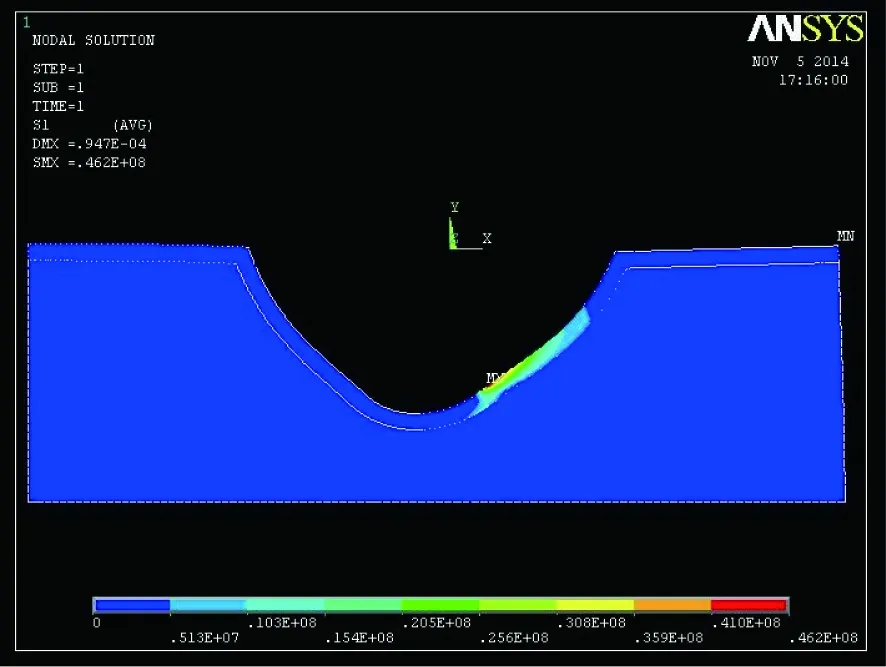
图5 σ1主应力云图

图6 σ2主应力云图

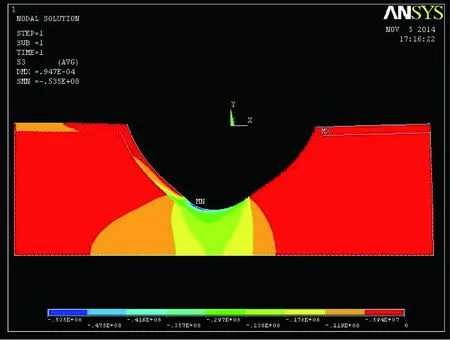
图7 σ3主应力云图

应力对比结果见表2。

表2 应力比较 MPa

①—接触应力；②—有限元分析

从应力云图及应力比较表结果可以看出：只有分布范围很小的局部出现拉应力，高压应力区域也不大，整体上对结构性能影响小；接触应力结果较有限元分析结果主压应力在数值上偏大，主拉应力稍小。有限元选取铰座及周边混凝土作为分析实体，分析范围大，面内单元间变形协调。力学分析假定选取单元体受其周边材料弹性约束，接触范围较远区域不纳入计算，接触面内变形范围很小，距离接触面较远处应力分布及变形骤减，拉应力值受到影响偏小，压应力结果偏大。实际运用中往往按保守考虑周边约束，即假定接触范围以外无变形，这对于主要承压的铰座构件计算是偏于安全的。

拱肋合龙后转动铰立即被二次浇筑封闭形成无铰拱体系，后期施工及运营阶段荷载主要由拱肋传递给拱座承担，铰座接触状态只要满足竖转施工的受力要求即可。对于这样在竖转期间主要承压的铰座受力构件而言，接触应力计算的结果已满足规范要求，压应力数值上具有一定安全储备，能够满足实际工程需要。图8为竖转工作实景。

4 结论

(1)在考虑摩擦力情况下的竖转铰座设计，通过建立在拓展接触理论之上的力学分析，计算较方便，强度满足规范要求。通过有限元分析建立模型进一步分

图8 竖转工作实景

析铰座的受力行为，证实了对于竖转施工中主要承压的铰座构件接触应力的分析结果能够满足实际工程需要，可用于指导工程设计。

(2)本工程拱肋从开始竖转施工到合龙段顺利完工历时9 d，过程采用国内先进的计算机液压同步提升技术同步液压提升控制系统[11-12]，并辅以动态控制，监控显示铰座工作状态良好。施工应用证明竖转铰座设计安全可行，可以应用到实践中去，在同类型桥梁结构设计方面积累了一定经验。在竖、平转设计中也可参考同样方法，对于同类型工程设计有一定借鉴作用。

[1] 尹紫红，董启军，卢演慧.西江特大桥连续刚构-柔性拱拱肋竖转设计与施工[J].铁道建筑，2012(5):26-28．

[2] 徐升桥.丫髻沙大桥主桥设计研究[J].铁道标准设计，2001(6):1-7．

[3] 王晓云.竖转铰的制作及安装[J].公路交通科技(应用技术版)，2008(2):21-22，31．

[4] 钱伟长.弹性力学[M].北京:科学出版社，1956：322-329．

[5] 孙林松，王德信，谢能刚.接触问题有限元分析方法综述[J].水利水电科技进展，2001(3):18-20．

[6] 黄海，厉海洋，罗齐汉.点线啮合齿轮最大接触应力计算的研究[J].机械设计，2011(4):65-68．

[7] 陈伟庆.斜拉索耳板锚固结构接触应力分析[J].铁道建筑技术，2003(6):5-7．

[8] 申兆繁.丫髻沙大桥主桥竖转铰设计[J].铁道标准设计，2001(6):26-29．

[9] 刘鸿文.材料力学(上册)[M].3版.北京:高等教育出版社，1992：284-318．

[10]中华人民共和国铁道部.TB10002.2—2005铁路桥梁钢结构设计规范[S]. 北京:中国铁道出版社，2005．

[11]李艳明，肖飞.丫髻沙大桥主桥竖转施工控制技术[J].铁道标准设计，2001(6):30-32．

[12]彭立志，李德钦，刘炜，等.佛山东平大桥竖转施工工艺的设计特色[J].公路，2006(3):139-145.

Stress Analysis of Free Bearing of Intercity Railway Continuous Beam Arch Bridge

FENG Fei

(China Railway Engineering Consulting Group Co.， Ltd.， Beijing 100055， China)

Based on the free bearing of a newly built intercity railway continuous beam arch bridge， the stress of free breaing elements is analyzed with contact theory， and a Ansys solid mechanical model is established to further analyze hinged support under vertical turning stress. The conclusion shows that the strength of the free breaing meets the design requirement under the most unfavorable load， and the stress calculation results are identical to finite element analysis. The engineering practices demonstrate that it is practical to use contact theory for similar project design.

Intercity railway; Continuous beam arch bridge; Free bearing; Contact theory; Finite element analysis

2014-10-23；

2014-11-24

冯 飞(1979—)，男，工程师，工学硕士，E-mail：ff2662@163.com。

1004-2954(2015)07-0105-03

U445.465

A

10.13238/j.issn.1004-2954.2015.07.023