Hybrid Grid DSMC Method for Chemical Nonequilibrium with Rarefied Flow Heating
Qu Cheng(屈程),Wang Jiangfeng(王江峰)
(College of Aerospace Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,P.R.China
Hybrid Grid DSMC Method for Chemical Nonequilibrium with Rarefied Flow Heating
Qu Cheng(屈程),Wang Jiangfeng(王江峰)*
(College of Aerospace Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,P.R.China
The influence of chemical nonequilibrium on the thermal characteristics is explored by using the 2D hybrid grid direct simulation Monte Carlo(DSMC)parallel method.An improved molecule search algorithm is proposed,which can preserve the high efficiency of area search algorithm.This method can overcome the defects of area search algorithm,and give all information about molecules hitting surface.The heat flux calculation method for a rarefied hypersonic flow is established.In addition,the testing methods of chemical reaction probability for five species of mixed gas with limited speed chemical reactions are also selected.To validate the effectiveness of the present method,hypersonic flow around a cylinder is firstly simulated,and subsequently numerical simulations of the heat flux and flow field characteristics around the blunt body at different heights are carried out in two different cases:the thermal nonequilibrium condition and the thermochemical nonequilibrium condition.Numerical results demonstrate the validity and reliability of the proposed methods.
hybrid grid;chemical nonequilibrium;heat flux;search algorithm;DSMC;parallel algorithm
0 Introduction
The predication accuracy of thermal characteristic plays an important role in aircraft thermal design.For a rarefied hypersonic flow,chemical nonequilibrium[1]affects flow field characteristics of aircraft due to the strong chemical reactions such as dissociation,composite,exchange and ionization[2-4].Owing to the complexity in flight environment and the limitation of experiment equipment,numerical methods have been applied to investigate hypersonic rarefied flow.So far,direct simulation Monte Carlo(DSMC)method of Bird[5-6]has been widely considered to be the most effective way to calculate aerodynamic parameters for hypersonic rarefied flow.Although DSMC method has been studied for over fifty years,there are still many areas to be investigated.
The influence of chemical nonequilibrium on thermal characteristics is studied,based on 2D hybrid grid DSMC parallel method.Firstly,heat flux calculation method of rarefied hypersonic flow under thermochemical nonequilibrium condition is established.Secondly,following the highly disordered characteristics of hybrid grid,an improved molecule search algorithm is developed,by which high efficiency of area search algorithm is fully preserved and defects of area search algorithm can be overcome perfectly.Thirdly,testing methods of chemical reaction probability of five species mixed gas with limited speed chemical reactions are selected.Then,based on 2D hybrid grid with message passing interface(MPI)parallel algorithms,DSMC calculation is coded and subsequently numerical simulations are given.Finally,conclusions are given and future research directions are pointed out.
1 Heat Flux Calculation Method of Rarefied Flow
With the failure of continuous medium hy-pothesis,heat flux can no longer be expressed by lower macroscopic temperature.To express heat flux related to molecular energy,macro-statistics of microscopic particles in flow field are needed.
As shown in Fig.1,d S is the area of an infinitesimalsurface,l the normal unit vector,and f(c,r,t)the molecule speed distribution function.To observe molecules within speed d c nearby c,it is obvious that molecules move across d S in a cylinder with base d S and height c d t from t to t+d t.The number of molecules mentioned above can be expressed as
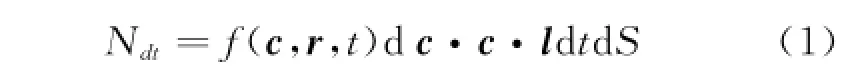
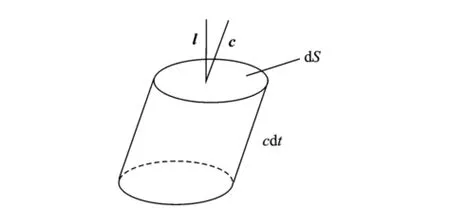
Fig.1 Volume of molecules at the beginning
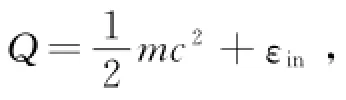
Flow parameters on aircraft surface are counted according to information carried by incident and reflection molecules,such as molecule number flux,momentum flux and energy flux.The heat flux on aircraft surface can be calculated by the energy difference of incident and reflection molecules per unit area and per unit time,defined as
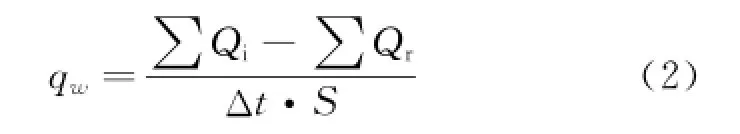
where the subscript"i"represents the incident molecules and"r"the reflection molecules.Δt is the action time and S the action area.
2 Hybrid Grid Search Algorithms
2.1 Area search algorithm
Fig.2 shows a triangular element P1P2P3and a quadrilateral element P1P2P3P4in hybrid grid,here,P is a point within the computing domain. P1P2P3and P1P2P3P4are arranged counterclockwise.If Sabcis defined as the vector area in the sequence'a→b→c',area coordinates of P can be written as(SP1P2P,SP2P3P,SP3P1P)and(SP1P2P,SP2P3P,SP3P4P,SP4P1P).There must exist a negative area if P lies outside the cell,such as SP2P3Pin Figs.2(a,b).The basic ideas in the area search algorithm are as follows:
To coordinate the simulated molecule afterΔt and its initial cell,each area coordinate of the simulated molecule can be determined.If all coordinates are positive,it means the simulated molecule is still in the initial cell.Negative coordinate denotes that the neighbor cell of the edge should be searched.Finally,a target cell of the simulated molecule can be found.
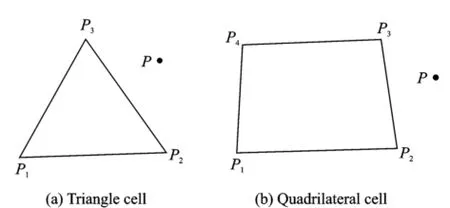
Fig.2 Sketch map of molecule search
2.2 Improved molecule search algorithm
Area search algorithm is efficient,but it still has some deficiencies and defects.One is that during the tracking process of the simulated molecule,its search path mostly goes along with the curve line,thus increasing the computational cost.The reason is that the area coordinates of a specific cell perhaps have more than one negative value.The other is that program cannot work when the searching path comes across the wall boundary,due to the absence of neighbor cell of the wall.
Considering the high disorder of hybrid grid,an improved search algorithm is presented,bywhich the high efficiency of area search algorithm is fully preserved and the defects of area search algorithm can be overcome perfectly.The main ideas of the algorithm are as follows:
The simulated molecule moves from P to Q,as shown in Fig.3.
Step 1 The number of cell edges can be obtained on the basis of the shape of initial cell for the simulated molecule.Then the area coordinate should be calculated.For each edge,a new triangle can be formed by connecting the edge’s starting point,ending point and Q.As mentioned above,if all area coordinates are positive,Q is still in the initial cell,and then searching should be stopped.If a negative value appears in the area coordinates,Q is on the outboard of the corresponding edge.Subsequently,it is determined whether PQ intersects with the corresponding edge.On the one hand,it is decided whether the edge has an adjacent cell if there exists an intersection point.If no adjacent cell exists,then go to Step 3.If an adjacent cell exists,it should search the neighbor cell of the edge,then turn to Step 2.On the other,the next edge should be checked if there exist no intersection points.
Step 2 The process of the adjacent cell of the above initial cell is similar to Step 1.Until the cell belonging to Q is found,searching stops.
Step 3 According to the nature of the edge,it is to determine whether it belongs to wall boundary or far field boundary.If it belongs to far field boundary,the simulated molecule has moved out of the flow field.Then the simulate molecule should be deleted and searching stops. If it belongs to wall boundary,information about the position of intersection should be obtained,then turn to Step 4.
Step 4 The subprogram is run,thus returning all information about the molecules hitting surface and the cell belonging to Q,then searching stops.
3 Numerical Model
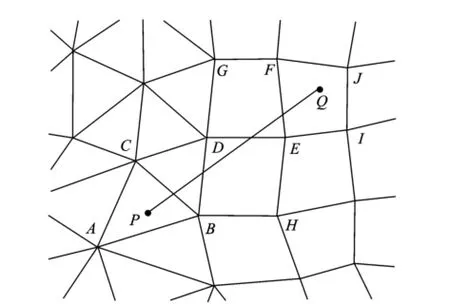
Fig.3 Sketch map of molecule search
The variable soft sphere(VSS)model[7]is used in this paper.The model can ensure not only the consistency of viscous coefficient and temperature but also the match of viscous and diffusion collision cross section for the inverse power law model.
No time counter(NTC)method[8]suggested by Bird is used in this paper.All possible collisions in the computational grid are considered directly.
The complete diffuse reflection model[2]is used.The velocity distribution function of diffuse reflection molecule can be expressed as
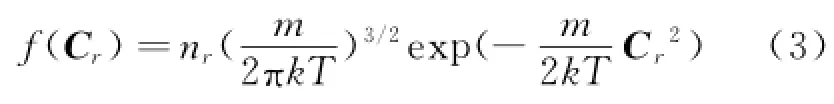
When dealing with rarefied flow heating under the chemical nonequilibrium condition,five species of molecules with no ionization are considered.The 23 species of chemical reactions such as dissociation,replacement and composite are considered as follows
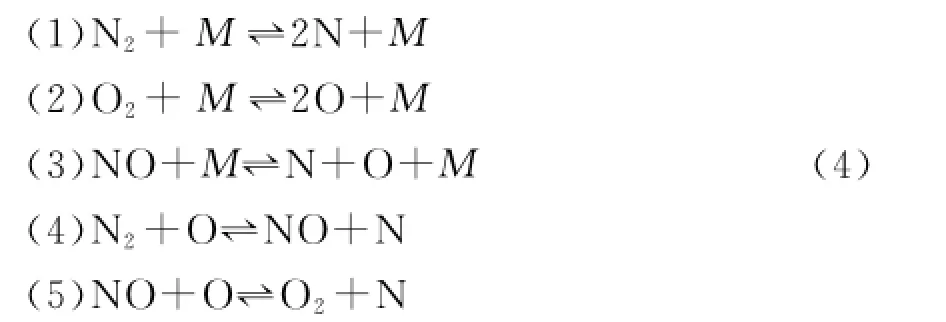
where M represents a catalyzer,and it can be any kind of five species molecules.It is assumed that chemical reactions will not change the nature of catalyzer.Chemical reactions and internal energy relaxation in inelastic collisions are coupled together in this paper.Conditions for chemical reactions are used as follows:
(1)Dissociation reaction:Theory of vibration relaxation in the Larsen-Borgnakke(L-B)model is adopted here.Dissociation reaction happens when vibration level of a molecule is excited to the level corresponding to its splitting energy.
(2)Composite reaction:Phenomenological theory of chemical reaction model is employed. The sampling rate is determined by partition function and balance collision theory[9].The calculation formula is:σR/σT=An TB,whereσRthe reaction cross-section andσTthe total collision cross-section.A and B are constants,whose values can be found in Ref.[9]for different composite reactions in air.
(3)Replacement reaction:The binary collision theory in Ref.[5]is used to determine the probability of occurrence in replacement reaction. Each kind of replacement reaction probability is accumulated during collisions.Replacement reaction happens when its reaction probability is greater than 1.
4 Numerical Results and Analysis
4.1 Hypersonic flow around cylinder
In order to verify the reliability of heat flux calculation method developed in this paper,the hypersonic flow around cylinder is simulated under the flow conditions given in Ref.[10]at the height of 80,85,90 km.Fig.4 shows the calculation model and boundary conditions.
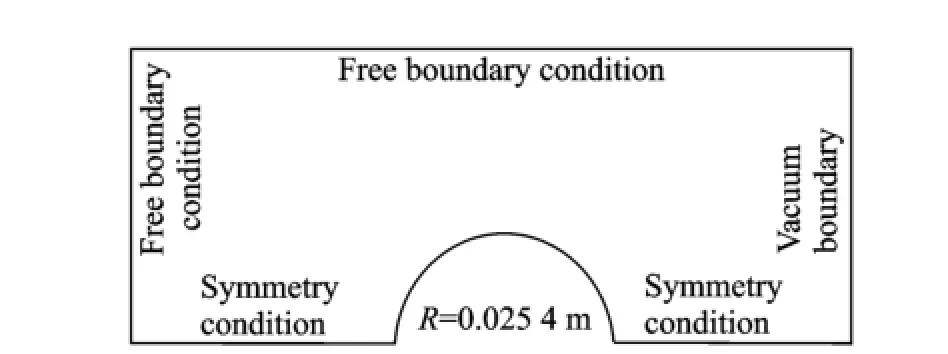
Fig.4 Schematic diagram and boundary conditions
In Table 1,one compares the heat fluxespresented by this paper with those(q0)by Ref.[10]at stagnation point under the different conditions,respectively.It can be seen that the heat fluxes at stagnation point calculated in this paper agrees well with those from the experiment in Ref.[10].
Fig.5 shows the temperature distribution along stagnation point line in the hypersonic flow around a cylinder.The computational condition is given in Ref.[10]at the height of 80 km.It can be seen from Fig.5 that the present results are in good agreement with those from the experiment in Ref.[10].
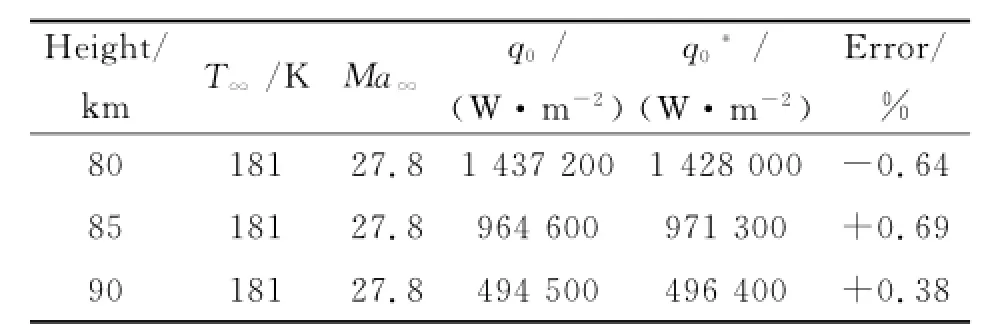
Table 1 Heat flux at stagnation point for cylinder
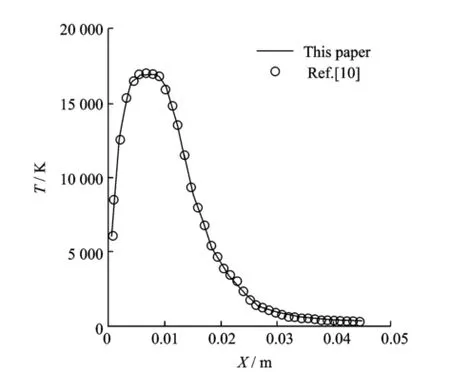
Fig.5 Temperature on stagnation streamline at 80 km
4.2 Hypersonic flow around blunt body
Mach number of blunt body is 27.8,attack angle is 0°and wall temperature Tw=1 000 K. The molecule percentage of flow components at the height of 80 km is N2:O2=0.763:0.237,while the molecule percentage of flow components at the height of 90 km is N2:O2:O=0.788:0.209:0.003.Fig.6 shows the shape of blunt body,grid partitions and parts of hybrid grid.
Table 2 shows the parallel efficiency for a blunt body case under the thermochemical nonequilibrium condition at the height of 80 km.It implies that the parallel algorithm in this paper can save computing cost.

Table 2 Parallel efficiency
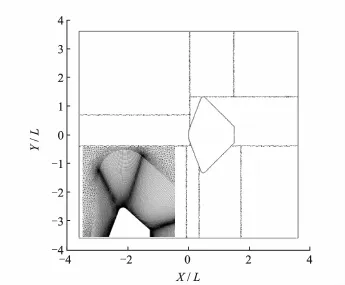
Fig.6 Shape of blunt,grid partitions and part of hybrid grid
Table 3 shows the executing time every 100 steps for a blunt body case under the thermochemical nonequilibrium condition at the height of 80 km using two different molecule search algorithms.The calculation condition and the computer configuration remain unchanged.The improved molecule search algorithm in this paper can shorten the computing time effectively.

Table 3 Executing time every 100 steps
Fig.7 shows the flow field temperature distribution at the height of 80 km under two different nonequilibrium conditions.The distribution of flow field temperature in Fig.7(b)basically agrees well with that from Ref.[5].Compared Fig.7(a)with Fig.7(b),it is clear that the chemical nonequilibrium can cause a notable dropin the flow temperature.
Fig.8 shows the density on stagnation streamline for blunt body at the height of 80 km under two different nonequilibrium conditions.It is obvious that shock wave captured by chemical nonequilibrium is closer to the stagnation point of wall than that done by thermal nonequilibrium.
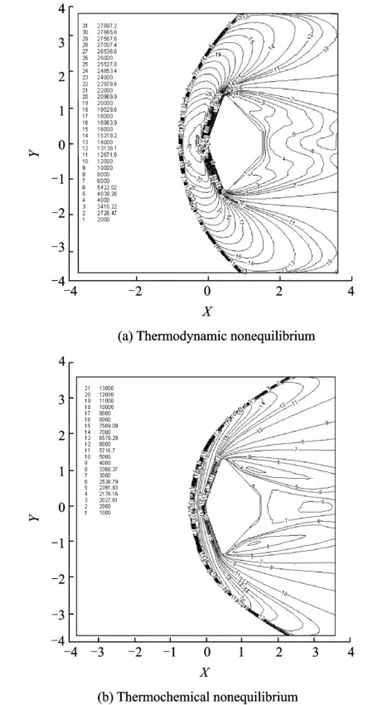
Fig.7 Temperature distribution at 80 km
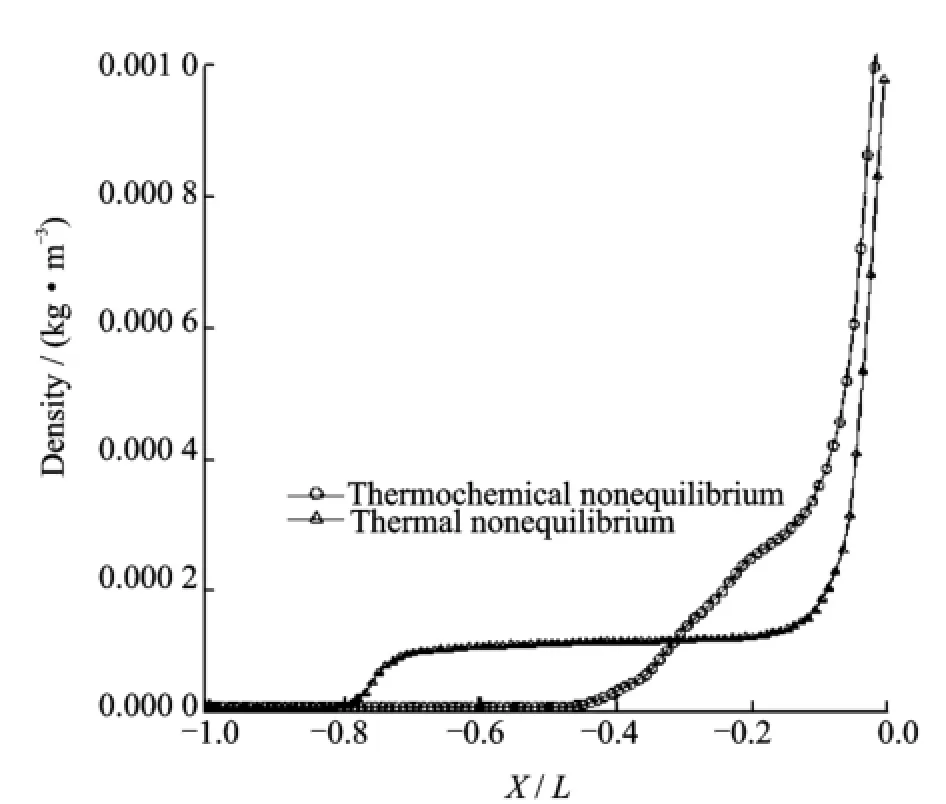
Fig.8 Density on stagnation streamline at 80 km
Fig.9 shows the temperature on stagnation streamline of the blunt body at the height of80 km and 90 km under two different nonequilibrium conditions,respectively.The distance from shock layer to stagnation point increases with the increase of height,as shown in Figs.9(a,b).It manifests that chemical nonequilibrium decreases the stagnation streamline temperature considerably.
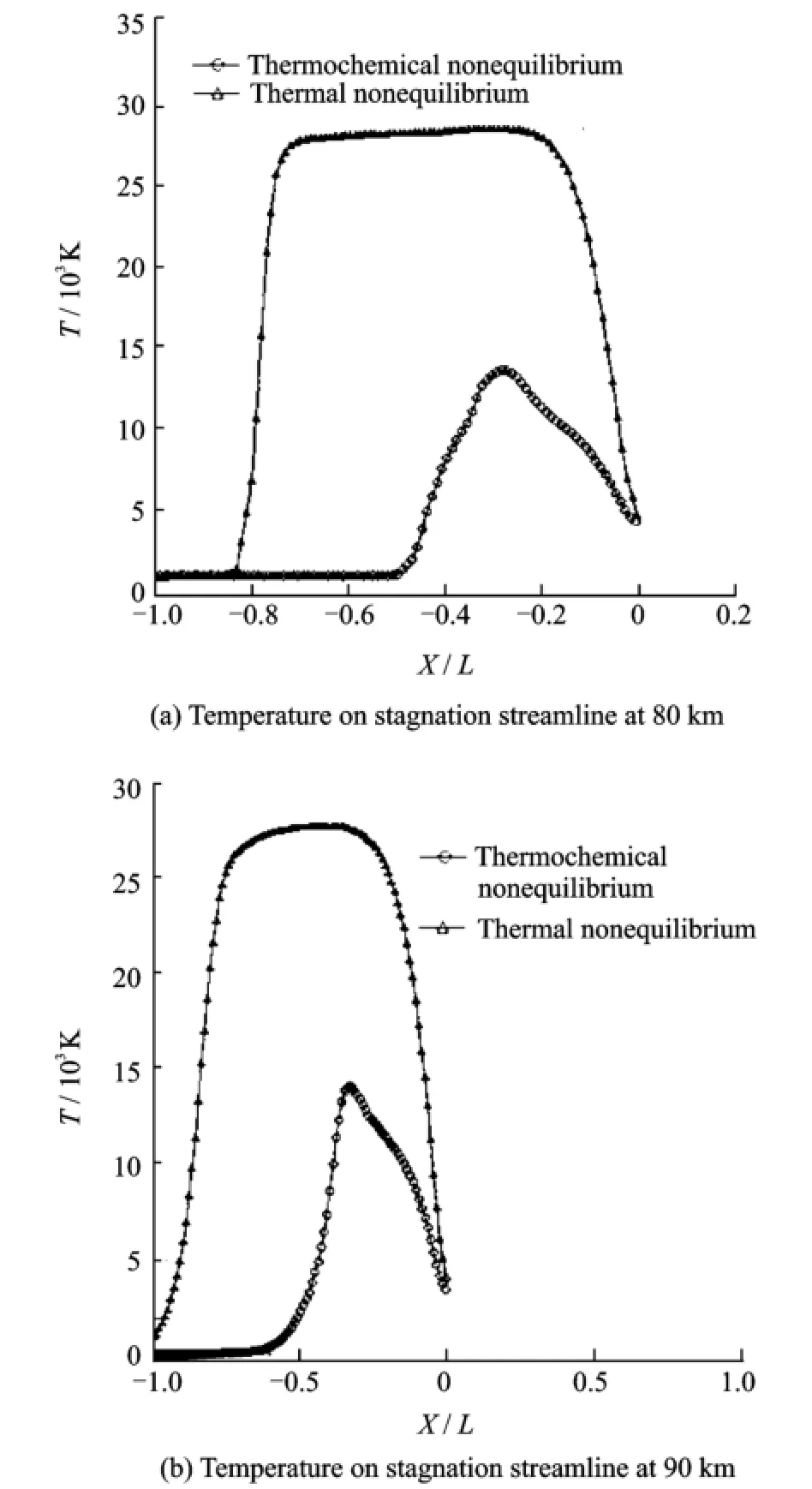
Fig.9 Temperature on stagnation streamline
Table 4 gives the heat fluxes at stagnation point at 80 km and 90 km under two nonequilibrium conditions.Here chemical nonequilibrium decreases the surface heat flux greatly.With the high temperature near the stagnation point,a lot of heat is absorbed by violent chemical reactions,thus leading to the decline of heat flux.In this example,the heat flux at stagnation point for thethermochemical nonequilibrium is 49.08%and 43.48%lower than that for the thermochemical nonequilibrium at 80 km and at 90 km,respectively.It indicates that the chemical nonequilibrium effect on heat flux has a weakening trend with the increase of height.
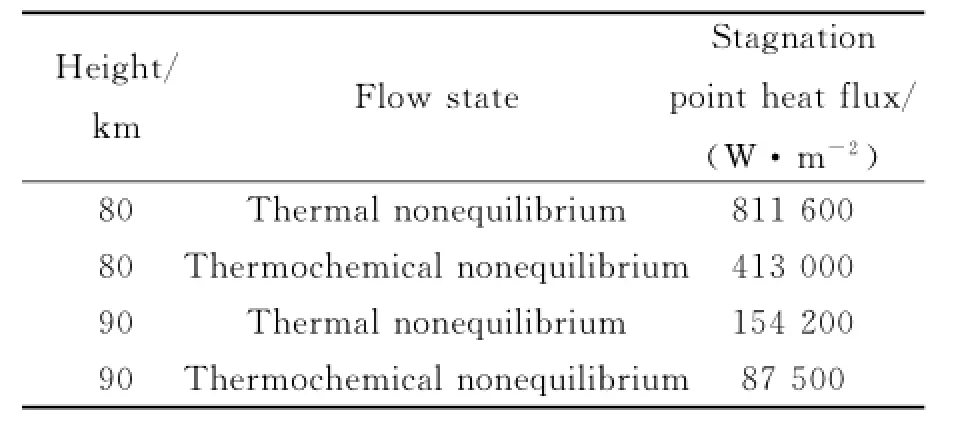
Table 4 Stagnation point heat flux of blunt body
Fig.10 shows the heat flux distribution of blunt body's mother line along X direction at 80 km under two nonequilibrium conditions.A peak heat flux exists at the stagnation point and a sharp drop starts from the stagnation point to the windward side.It is mainly because the curvature radius on stagnation point is much smaller than that on the front wall.Heat flux on the windward surface linearly descends,while heat flux on the leeward surface sharply drops.The main reason is that density of molecules number on the leeward surface is much smaller than that near the front wall.Thus the wall heat flux obtained by statistical method is much smaller,which agrees well with the true physical process.
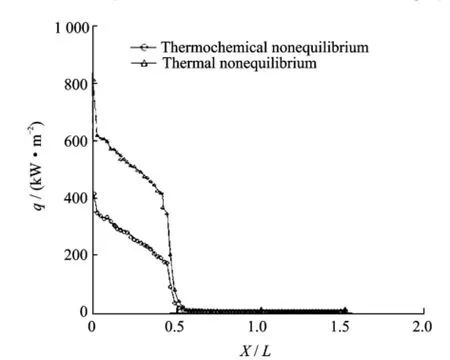
Fig.10 Heat flux along symmetric plane at 80 km
In Fig.10,the heat flux distribution trends of blunt body's windward mother line are largelyconsistent with those under two nonequilibrium conditions.The surface heat flux of blunt body under the thermochemical nonequilibrium condition is much lower than that under the thermochemical nonequilibrium condition,due to the absorption by chemical reactions.
5 Conclusions
Based on 2D hybrid body-fit grid DSMC parallel method,the influence of chemical nonequilibrium on thermal characteristics in hypersonic rarefied flow is investigated.The heat flux calculation method of rarefied hypersonic flow and the DSMC program are established.An improved search algorithm applied to hybrid grid is presented.High efficiency of area search algorithm can be fully preserved.Meanwhile,all information about molecules hitting surface can be given.The following conclusions are drawn:
(1)Molecular tracking and search algorithm for hybrid grid are studied and in the search algorithm no special grid structure is required.
(2)To validate the presented algorithm,numerical calculations are carried out.Aerodynamic heat features around blunt body at different heights and flow states are analyzed.Numerical results agree well with those from references,proved the validity and reliability of the heat flux calculation method proposed in this paper.
(3)To provide basic technical for accurate aerodynamic heat prediction in the rarefied flow,numerical research about 3D rarefied flow DSMC method with ionization reactions on hybrid grid is to be done in the future work.
Acknowledgement
This work was supported by the National Defense Basic Research Program during the Twelfth Five-Year Plan Period.
[1] Shen Qing.Rarefied gas dynamics[M].Beijing:National Defence Industry Press,2003.(in Chinese)
[2] Bird G A.Molecular gas dynamics and the direct simulation of gas flow[M].Oxford,England:Clarendon Press,1994.
[3] Wu Qifen.DSMC method for thermochemical nonequilibrium in high temperature rarefied flow[M]. Changsha:National University of Defense Technology Press,1999.(in Chinese)
[4] Boyd L D.Rotational and vibrational nonequilibrium effects in rarefied,hypersonic flows[J].Journal of Thermophysics and Heat Transfer,1990,4(4):478-484.
[5] Wang Xuede.DSMC method on unstructured grids for hypersonic rarefied gas flow and its parallelization[D].Nanjing,China:Nanjing University of Aeronautics and Astronautics,2006.(in Chinese)
[6] Liou W W,Fang Y.Heat transfer in microchannel devices using DSMC[J].JMEMS,2001,10:274-279.
[7] Kim M,Gulhan A.Modeling of electron temperature in hypersonic flows[C]∥49th AIAA Aerospace Sciences Meeting.Orlando,Florida:AIAA,2011.
[8] Allen J,Hauser T.foam DSMC:An object oriented parallel DSMC solver for rarefied flow applications[C]∥45th AIAA Aerospace Sciences Meeting and Exhibit.Reno,Nevada:AIAA,2007.
[9] Koura K,Matsumoto H.Varibal soft sphere model for air species[J].Phys Fluids,1992,A4:1083-1085.
[10]Fan Jing,Shen Qing.The Monte Carlo direct simulation of the hypersonic nonequilibrium flow past a circular cylinder in transition regime[J].Acta Aerodynamic Sinca,1995,13(4):406-413.(in Chinese)
(Executive editor:Zhang Tong)
O356 Document code:A Article ID:1005-1120(2015)04-0408-07
*Corresponding author:Wang Jiangfeng,Professor,E-mail:wangjf@nuaa.edu.cn.
How to cite this article:Qu Cheng,Wang Jiangfeng.Hybrid grid DSMC method for chemical nonequilibrium with rarefied flow heating[J].Trans.Nanjing U.Aero.Astro.,2015,32(4):408-414.
http://dx.doi.org/10.16356/j.1005-1120.2015.04.408
(Received 5 January 2014;revised 19 February 2014;accepted 25 March 2014)
 Transactions of Nanjing University of Aeronautics and Astronautics2015年4期
Transactions of Nanjing University of Aeronautics and Astronautics2015年4期
- Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Control of Vehicle Active Front Steering Based on Active Disturbance Rejection Feedback Controller
- A Hydrodynamic Model for Dimpled Mechanical Gas Seal Considering Interaction Effect
- Resolution Increase and Noise Removal in Particle Size Distribution Measurement with Shifrin Transform
- Experiments on an Open-Loop Cycle Carbon Dioxide Refrigeration System
- Real-Time Rendering of Dynamic Clouds Using Multi-Resolution Adaptive Grids
- Dynamic Surface Control with Nonlinear Disturbance Observer for Uncertain Flight Dynamic System
