A Preconditioned Gridless Method for Solving Euler Equations at Low Mach Numbers
Cao Cheng(曹骋),Chen Hongquan(陈红全)*
College of Aerospace Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,P.R.China
A Preconditioned Gridless Method for Solving Euler Equations at Low Mach Numbers
Cao Cheng(曹骋),Chen Hongquan(陈红全)*
College of Aerospace Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,P.R.China
A preconditioned gridless method is developed for solving the Euler equations at low Mach numbers.The preconditioned system in a conservation form is obtained by multiplying a preconditioning matrix of the type of Weiss and Smith to the time derivative of the Euler equations,which are discretized using a gridless technique wherein the physical domain is distributed by clouds of points.The implementation of the preconditioned gridless method is mainly based on the frame of the traditional gridless method without preconditioning,which may fail to converge for low Mach number simulations.Therefore,the modifications corresponding to the affected terms of preconditioning are mainly addressed.The numerical results show that the preconditioned gridless method still functions for compressible transonic flow simulations and additionally,for nearly incompressible flow simulations at low Mach numbers as well.The paper ends with the nearly incompressible flow over a multi-element airfoil,which demonstrates the ability of the method presented for treating flows over complicated geometries.
gridless method;preconditioning;Euler equations;cloud of points
0 Introduction
In the past few decades,computational fluid dynamics(CFD)has gained sustained development and has become an important tool in modern aircraft design.The computational domain used in CFD is discretized by cells of grid or mesh,particularly for existing commercial CFD software.The corresponding methods can be named as"grid method",which requires a grid generation step before flow simulations.For a complicated geometry like a full modern aircraft,to generate a suitable grid is still of great challenge due to the connectivity limitation of the grid,particularly to cope with some geometric details like small gaps between multi-bodies.Hence,the idea of being free of grids has drawn attention.To eliminate completely the limitation of the grid connectivity with point based discretization,a class of methods,namely"gridless or grid-free method",was developed,which behaves naturally and more flexibly to cope with the flow past any complicated geometry due to the following facts.The spatial derivative approximation at any given point by gridless methods depends only on the information of its surrounding points which do not need to form a mesh.The point distribution in the computational domain can be made by using any existing means like the ones used in existing structured or unstructured grid generators.The interesting features motivated many researchers to study this issue and various grid-free approaches[1-10]have been proposed.In aerodynamics,the most notable work was done by Batina[1],who developed an explicit solver based on the centered scheme with artificial dissipation for solving compressible flows with shocks.An implicit solver was later developed by Morinishi[5]using"midpoint upwind"and weighted least-squares.Most of above gridless methods are usually developed for compressible flows and can not be extendeddirectly for solving nearly incompressible flows at low Mach numbers.
Here a further extension of traditional gridless method will be considered to develop a preconditioned gridless method for solving Euler equations at low Mach numbers.A preconditioning matrix of the type of Weiss and Smith is selected.The preconditioned system in conservation form is then obtained by multiplying preconditioning matrix to the time derivative of the Euler equations,which are discretized using a gridless technique wherein the physical domain is distributed by clouds of points.The implementation of the preconditioned gridless method is mainly based on the frame of the traditional gridless method without preconditioning,therefore the only modifications corresponding to the affect terms of preconditioning are mainly discussed. The resulting preconditioned gridless method is tested and analyzed by both compressible transonic flows and nearly incompressible flows at low Mach numbers over airfoils or multi-element airfoils.The numerical results show that the preconditioned gridless method still functions for compressible transonic flow simulations and additionally,for nearly incompressible flow simulations at low Mach numbers as well.
1 Governing Equations
The Euler equations governing inviscid flows can be expressed in a dimensionless[10]conservative form as
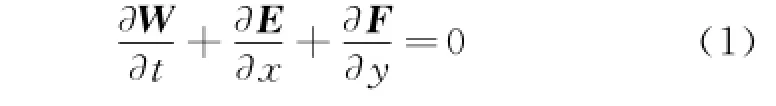
where W is the vector of conservative variables.E and F are the convective flux terms.They are defined as
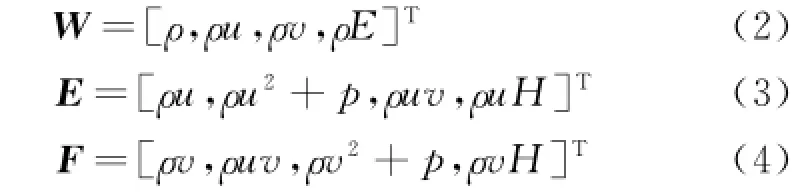
whereρ,p,E and H denote the density,pressure,total energy per unit mass,and total enthalpy per unit mass respectively.u and v are the Cartesian components of the velocity vector. These quantities for a perfect gas satisfy
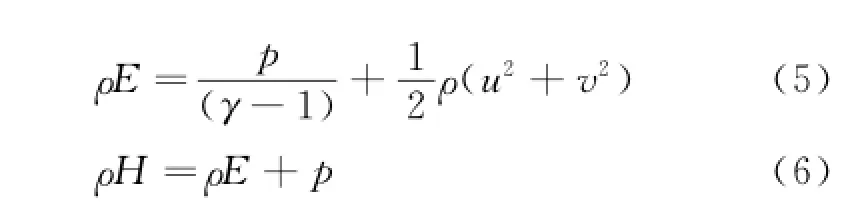
whereγis the ratio of specific heats of the fluid and typically taken asγ=1.4 for air.
2 Basic Gridless Method Without Preconditioning
In the gridless method,scattered points are distributed in the physical domain of the problem to be solved.For each point,several points around it are chosen to form a cloud of points[1-4]. Fig.1 shows a typical cloud of points C(i),in which point i is named the center and the other points are called the satellites.

Fig.1 Cloud of points
The spatial derivatives of any quantities in the gridless method are evaluated with linear combinations of certain coefficients and the quantities in the cloud of points.The first order derivatives of function f at point i can be estimated by the following linear combination forms[11]
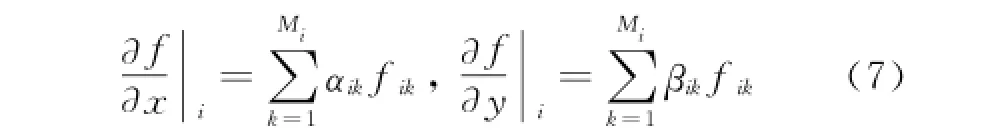
where Midenotes the total number of the satellites in the cloud C(i),and fikthe value at the midpoint between point i and point k.The coefficientsαikandβikcan be obtained using weighted least-squares curve fitting[5,12-13].The weight functions used in this study are given by

where rkis the relative distance defined with
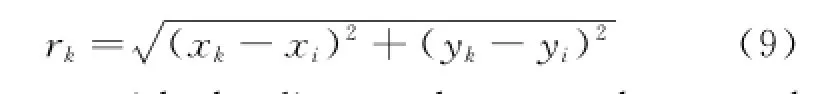
In cloud C(i),the flux terms of Eq.(1)can be rewritten as
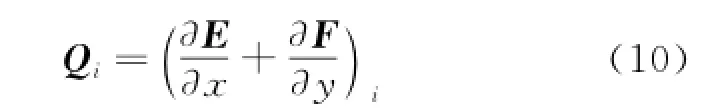
If Eq.(7)is applied to the convective flux of the Euler equations,it can be further written as
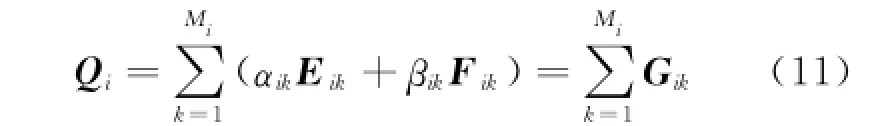
where the flux term G at the midpoint is defined as
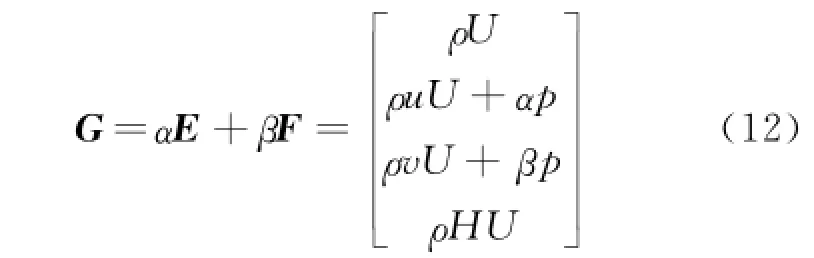
and U is defined as

The numerical flux Gikat the midpoint between point i and k can be calculated from the conservative variables at the midpoint.By using central difference method,the conservative variables at the midpoint can be obtained as follows

With the conservative variables Wik,the numerical flux Gikcan be calculated.To make the computation stable,the artificial dissipative term D is added.The semi-discretization form of the Euler equations for cloud C(i)then can be expressed as
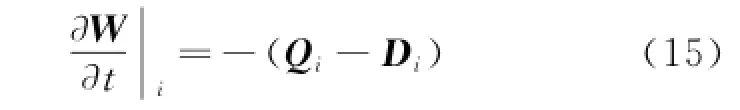
The construction of the artificial dissipative terms is given by
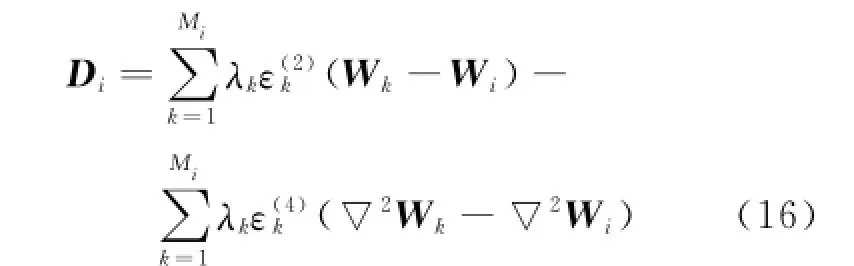
whereε(2)andε(4)are the adaptive coefficients.λ is the spectral radius of the Jacobian matrix A=∂G/∂W
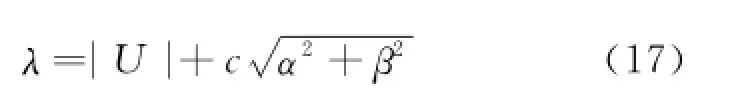

where the superscripts n and n+1 denote the current and the next new time level,respectively and m=1,2,3,4 is the internal step.The coefficients ηmcan be found in Ref.[14].To accelerate the convergence,Δtiis taken as the maximum permissible local time step[14]
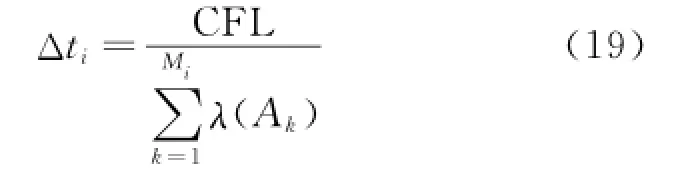
In the case of an inviscid flow,the fluid slips over the wall surface.In other words,the normal component of the velocity vanishes at the solid boundary.Therefore,the appropriate boundary condition is to require the flow to be tangential to the surface

where Vwand n are the velocity and unit normal vector at the surface,respectively.
In the far field,one-dimensional characteristic analysis based on Riemann invariants is used to determine the values of the flow variables on the outer boundaries of the computational domain.The details of the implementation of the boundary conditions can be found in Ref.[14].
3 Preconditioned Gridless Method
The preconditioned system is obtained by multiplying the time derivative in Eq.(1)by a matrixΓ
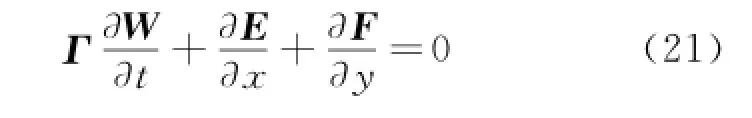
whereΓrepresents the preconditioning matrix based on the conservative variables.In a strict sense,Eq.(21)is not conservative for the timedependent flows.As pointed out in Ref.[15],however,it is still conservative in the steady state.Thus,it is not a problem to employ Eq.(21)for steady calculations.
The choice of the preconditioning matrix for low Mach number flows is not unique[16-21].Awell-known and widely used preconditioning matrix is introduced by Weiss and Smith[18-19].This paper uses the following preconditioning matrix and it can be written as
为使阿力木·亚库普度过眼前的难关,吴辉生根据他的特长协调联系给他在六建东方一分公司安排了一份司机的工作,月收入2500元。如今阿力木·亚库普有了稳定的工作,生活质量有了明显改善,他逢人便说,我能有今天多亏了汉族亲戚的帮助引导。
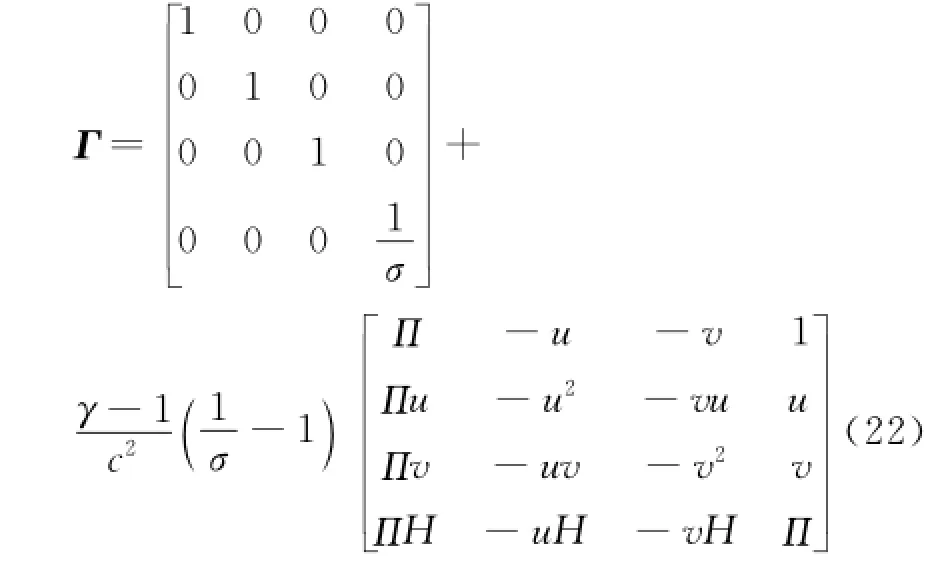
where
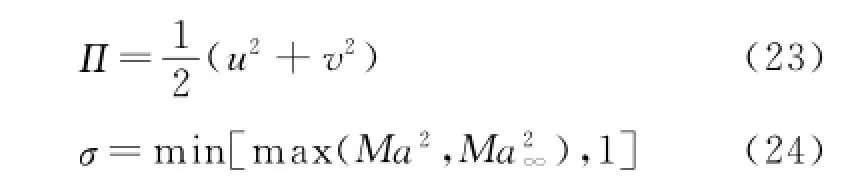
where Ma and Ma∞represent the local and the freestream Mach number,respectively.
The difficulty in solving the flows at a low Mach number of the traditional gridless method without preconditioning is associated with the large disparity in the magnitudes of eigenvalues[15].The application of preconditioning changes the eigenvalues of the system and scales them to the same order of magnitude.Using the gridless method to discretize the spatial derivatives as suggested in Eq.(7),Eq.(21)can be further rewritten as
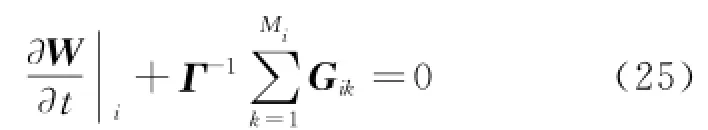
In Eq.(25),the flux terms can be computed using the traditional gridless method described in Section 1 and then multiplied byΓ-1directly. The Jacobian matrix for the system after preconditioning now becomesΓ-1∂G/∂W,which has the spectral radius as
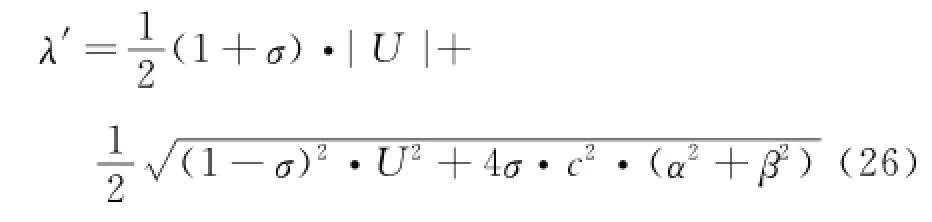
To make the computation stable,a new artificial dissipative term D'ishould be added and takes the form as
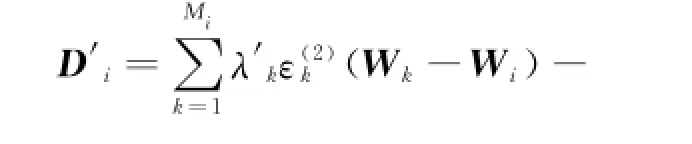
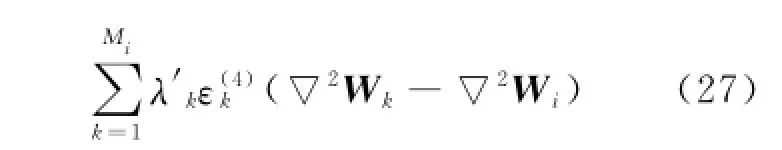
Compared with Eq.(16),adaptive coefficients,ε(2)andε(4)are now multiplied by a modified spectral radiusλ'defined in Eq.(26).Therefore,Eq.(25)can be rewritten as
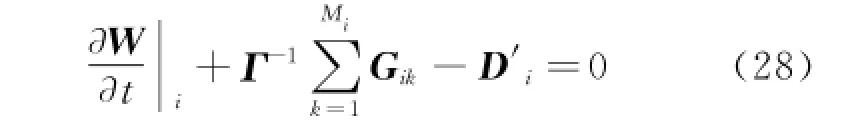
An explicit four-stage Runge-Kutta time integration scheme like Eq.(18)is also used for this resulting semi-discretization Eq.(28)to have a steady solution.The boundary conditions should also be changed to suit the preconditioned system.The use of characteristics-based boundary conditions requires information of the eigenvalues of the Jacobian matrix.Once the time-dependent equations are changed,the characteristics of the system are changed correspondingly. Hence,it is necessary to modify the far-field boundary conditions for the preconditioned system.Accurate characteristic boundary conditions for the preconditioned system can be found in Ref.[22].As for incompressible flows,a simplified boundary condition is proposed by Turkel[23]and adopted in this paper,which reads
Inflow:
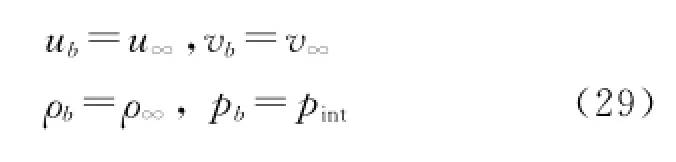
Outflow:
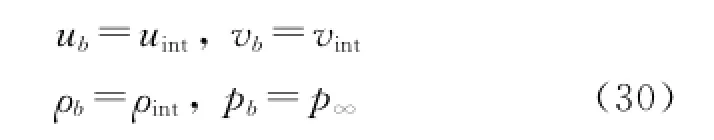
where the subscript"b"denotes the variables to be computed at the boundary,"int"the variables from the interior of the flowfield,and"∞"the freestream variables.
4 Numerical Results
The gridless method and preconditioned gridless method described above have been implemented and tested with different flow conditions.In this section one presents results obtained for the following test cases:transonic flows over NACA0012 airfoil,flows over airfoils at low Mach numbers,and nearly incompressible flow over a multi-element airfoil.The first result will showthe performance and accuracy of the present methods for computing transonic flows and the gridless method with preconditioning does not adversely affect the calculations of this type.The second case will demonstrate the preconditioned gridless method for solving the flows at low Mach numbers.And in the final case,the ability of present preconditioned gridless method is demonstrated for treating nearly incompressible flows over complex geometries.
4.1 Transonic flows over NACA0012 airfoil
In order to demonstrate the accuracy and performance of the present method for solving transonic flow,numerical results are presented for the calculation of two-dimensional flow around an NACA0012 airfoil.The clouds of 3 808 points used for this case are shown in Fig.2.In accordance with Ref.[24],the angle of attack is set to 0°and Mach number to 0.8.
Fig.2 Point distribution around NACA0012 airfoil
The surface pressure coefficients of the NACA0012 airfoil are shown in Fig.3.It is shown the reasonable agreement of the predictions obtained by the gridless method,preconditioned gridless method and finite volume method(FVM)[24]in view of the strength or location of the captured shock.
4.2 Flows over airfoils at low Mach numbers
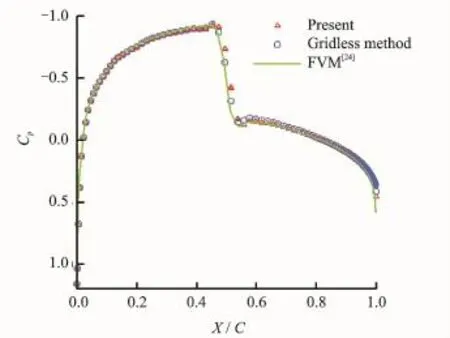
Fig.3 Surface pressure coefficients
The performance of the preconditioned gridless method has been tested firstly for the flows over the symmetric NACA 0012 airfoil at low Mach numbers.Four low Mach numbers of 0.3, 0.1,0.01 and 0.001 with the same zero angle of attack and CFL=6 are selected for the numerical simulation.Convergence histories for both gridless method and preconditioned gridless method are shown in Figs.4,5,respectively.
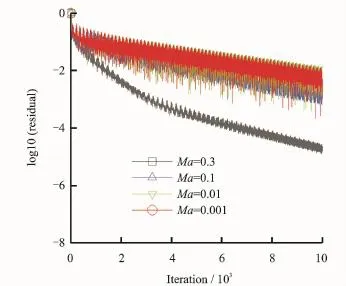
Fig.4 Convergence histories without preconditioning
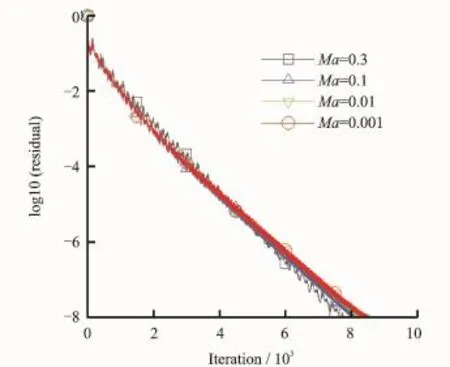
Fig.5 Convergence histories with preconditioning
Here it can be observed that the convergence of gridless method without preconditioning becomes difficulty as the Mach number becomes smaller.However,the preconditioned gridless method can be converged for all testing Mach numbers.Predicted Mach contours for the typical case of Ma=0.001,angle of attack 0°and CFL= 6 are shown in Fig.6.It can be noted that the symmetry of Mach contours is well captured in agreement with the physical symmetry flow field of the flows over the symmetric NACA 0012 airfoil with zero angle of attack.The corresponding distribution of surface pressure coefficient is compared with the experimental data[25]in Fig.7.As seen from Fig.7,the agreement between the calculation and experiment is quite good.
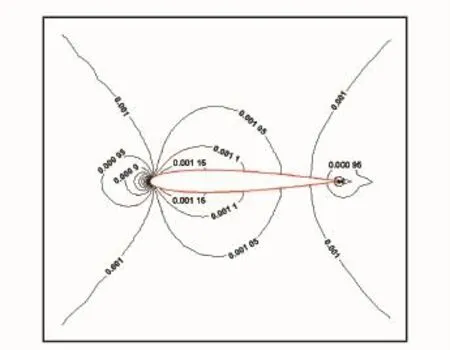
Fig.6 Mach contours

Fig.7 Distribution of surface pressure coefficient
The computations of the flows over an unsymmetric RAE2822 airfoil at low Mach number are also carried out by the present preconditioned gridless method.Here the case of Mach number 0.01 and angle of attack 1.89°is presented as shown in Figs.8—11.Fig.8 illustrates the clouds of points distributed in the computational domain.The convergence history of the present preconditioned gridless method in Fig.9 is plotted along with that of gridless method without preconditioning for having a possible comparison. It can be learned from the corresponding Mach contours in Fig.10 that the captured flow filed is now unsymmetric,which reflects the physical feature of the flows over an unsymmetric RAE2822 airfoil.As seen from Fig.11,agreement between present calculations and other results appeared in open literature like Puoti's calculations[26]or the experiment[27]is quite good in view of peak of leading edge suction and pressure distributions.
Fig.8 Points around RAE2822 airfoil

Fig.9 Comparison of convergence history

Fig.10 Mach contours around RAE2822 airfoil
4.3 Nearly incompressible flow over a multielement airfoil
As compared with the single-element airfoil like NACA 0012 or RAE2822 mentioned above,multi-element airfoils have relatively complicated geometry and are widely used as the techniques of high lift systems related to the landing or take-off of a real aircraft.It can be noted that the flows during the landing or take-off are nearly incompressible.Therefore,the simulation of nearly incompressible flow over a multi-element airfoil is conducted here to demonstrate the ability of the method developed in this paper.
The clouds of 5 865 points used for this case are shown in Fig.12.Here it can be learned that this multi-element airfoil consists of slat,main,and flap parts.To compare the results with the available results appeared in open literatures,the case of Mach number Ma=0.197 and angle of attack 4.01°is selected and computed with CFL= 6.Fig.13 shows the better convergence history of this calculation,along with plotting failing convergence history of gridless method without preconditioning.The Mach contours and the corresponding surface pressure coefficient are shown in Figs.14,15,respectively.A reasonable agreement between calculations and experimental data[28]of the surface pressure coefficient is achieved particularly on the surface of the main part of thismulti-element airfoil.
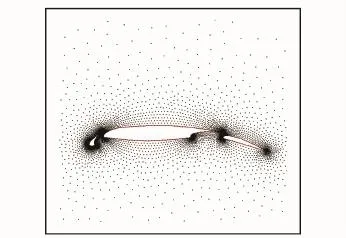
Fig.12 Point distribution around multi-element airfoil

Fig.13 Convergence histories
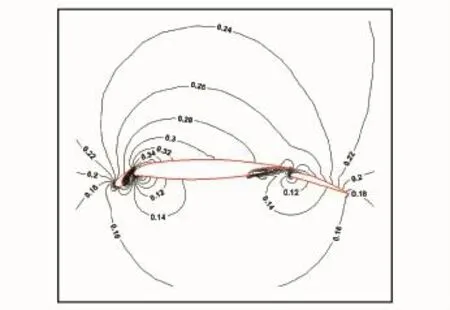
Fig.14 Mach contours

Fig.15 Surface Cpdistribution
5 Conclusions
The preconditioned gridless method for solving Euler equations has been developed based on the gridless method without preconditioning,which may fail to converge for low Mach number simulations.The preconditioned gridless method still adapts to compressible transonic flow simulations and additionally,for nearly incompressible flow simulations at low Mach numbers as well. The numerical results have shown the performance and the accuracy of the preconditioned gridless method,which demonstrates the ability for treating nearly incompressible flows over complex geometries.
Acknowledgement
This work was supported by the National Natural Science Foundation of China(No.11172134).
[1] Batina J T.A gridless Euler/Navier-Stokes solution algorithm for complex-aircraft applications[R]. AIAA 93-0333,Reno NV:AIAA,1993.
[2] Liu J L,Su S J.A potential gridless solution method for the compressible Euler/Navier-Stokes equations[R].AIAA 1996-0526,Reno NV:AIAA,1996.
[3] Onate E,Idelsohn S,Zienkiewicz O C,et al.A finite point method in computational mechanics:Applications to convective transport and fluid flow[J]. International Journal for Numerical Methods in Engineering,1996,39(22):3839-3866.
[4] Belytschko T,Krongauz Y,Organ D,et al.Meshless methods:An overview and recent developments[J].Computer Methods in Applied Mechanics and Engineering,1996,139(1):3-47.
[5] Morinishi K.An implicit gridless type solver for the Navier-Stokes equations[J].Computational Fluid Dynamics Journal,2001(S):551-560.
[6] Sridar D,Balakrishnan N.An upwind finite difference scheme for meshless solvers[J].Journal of Computational Physics,2003,189(1):1-29.
[7] Kirshman D J,Liu F.A gridless boundary condition method for the solution of the Euler equations on embedded Cartesian meshes with multigrid[J].Journal of Computational Physics,2004,201(1):119-147.
[8] Ma Zhihua,Chen Hongquan,Zhou Chunhua.A study of point moving adaptivity in gridless method[J].Computer Methods in Applied Mechanics and Engineering,2008,197(21/22/23/24):1926-1937.
[9] Katz A,Jameson A.A comparison of various meshless schemes within a unified algorithm[R].AIAA 2009-596,Orlando Florida:AIAA,2009.
[10]Pu Saihu,Chen Hongquan.Gridless method for unsteady viscous flows[J].Transactions of Nanjing U-niversity of Aeronautics&Astronautics,2012,29(1):1-8.
[11]Guo Tongqing.Transonic unsteady aerodynamics and flutter computations for complex assemblies[D]. Nanjing,China:College of Aerospace Engineering,Nanjing University of Aeronautics and Astronautics,2006.(in Chinese)
[12]Chen Hongquan,Shu Chang.An efficient implicit mesh-free method to solve two-dimensioanl compressible euler equations[J].International Journal of Modern Physics C,2005,16(3):439-454.
[13]Chen Hongquan.An implicit gridless method and its applications[J].Acta Aerodynamica Sinica,2002,20(2):133-140.(in Chinese)
[14]Morinishi K.Gridless type solution for high Reynolds number multielement flow fields[R].AIAA 95-1856,1995.
[15]Ma Zhihua.Research of adaptive meshfree and hybridized mesh/meshfree methods[D].Nanjing,China:Nanjing University of Aeronautics and Astronautics,2008.(in Chinese)
[16]Turkel E.Preconditioned methods for solving the incompressible and low speed compressible equations[J].Journal of Computational Physics,1987,72(2):277-298.
[17]Turkel E.A review of preconditioning methods for fluid dynamics[J].Applied Numerical Mathmatics,1993,12(1/2/3):257-284.
[18]Choi Y H,Merkle C L.The application of preconditioning to viscous flows[J].Journal of Computational Physics,1993,105(2):207-223.
[19]Weiss J,Smith W A.Preconditioning applied to variable and constant density flows[J].AIAA Journal,1995,33(11):2050-2057.
[20]Weiss J M,Maruszewski J P,Smith W A.Implicit solution of preconditioned Navier-Stokes equations using algebraic multigrid[J].AIAA Journal,1999,37(1):29-36.
[21]Han Zhirong,Lu Zhiliang,Guo Tongqing.Air-load calculation of wind turbine airfoil based on preconditioning and grid adaption technique[J].Journal of Nanjing University of Aeronautics&Astronautics,2011,43(5):586-591.(in Chinese)
[22]Turkel E,Radespiel R,Kroll N.Assessment of preconditioning methods for multidimensional aerodynamics[J].Computers and Fluids,1997,26(6):613-634.
[23]Turkel E,Fiterman A,Van Leer B.Preconditioning and the limit to the incompressible flow equations[R].NASA-CR-191500,Hampton VA:Institute for Computer Applications in Science and Engineering,1993.
[24]Jameson A,Mavriplis D.Finite volume solution of the two-dimensional Euler equations on a regular triangular mesh[J].AIAA Journal,1986,24(4):611-618.
[25]Liu Chen,Wang Jiangfeng,Wu Yizhao.Convergence characteristics of preconditioned Euler equations at low Mach numbers[J].Acta Aeronautica et Astronaut ica Sinica,2009,30(5):842-848.(in Chinese)
[26]Puoti V.Preconditioning method for low-speed flows[J].AIAA Journal,2003,41(5):817-830.
[27]Liang Zixuan,Ding Jue,Wen Peifen.Application of preconditioning and multi-grid technique to twodimensional flow calculation[J].Journal of Shanghai University,2011,17(2):158-163.(in Chinese)
[28]Rumsey C L,Thomas B,Ying S X,et al.Prediction of high-lift flows using turbulent closure models[R]. AIAA 97-2260,Atlanta GA:AIAA,1997.
(Executive editor:Zhang Tong)
V211.3 Document code:A Article ID:1005-1120(2015)04-0399-09
*Corresponding author:Chen Hongquan,Professor,E-mail:hqchenam@nuaa.edu.cn.
How to cite this article:Cao Cheng,Chen Hongquan.A preconditioned gridless method for solving Euler equations at low Mach numbers[J].Trans.Nanjing U.Aero.Astro.,2015,32(4):399-407.
http://dx.doi.org/10.16356/j.1005-1120.2015.04.399
(Received 16 July 2014;revised 23 August 2014;accepted 30 August 2014)
 Transactions of Nanjing University of Aeronautics and Astronautics2015年4期
Transactions of Nanjing University of Aeronautics and Astronautics2015年4期
- Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Control of Vehicle Active Front Steering Based on Active Disturbance Rejection Feedback Controller
- A Hydrodynamic Model for Dimpled Mechanical Gas Seal Considering Interaction Effect
- Resolution Increase and Noise Removal in Particle Size Distribution Measurement with Shifrin Transform
- Experiments on an Open-Loop Cycle Carbon Dioxide Refrigeration System
- Real-Time Rendering of Dynamic Clouds Using Multi-Resolution Adaptive Grids
- Dynamic Surface Control with Nonlinear Disturbance Observer for Uncertain Flight Dynamic System
