Dynamics and Attitude Error Analysis for Dock Test System of Small Satellite

Zhang Yuan（张元），Sun Lili（孙丽丽），Lai Yinan（赖一楠），Dai Ye（戴野）

School of Mechanical and Power Engineering，Harbin University of Science and Technology，Harbin 150080，P.R.China

Dynamics and Attitude Error Analysis for Dock Test System of Small Satellite

Zhang Yuan（张元）*，Sun Lili（孙丽丽），Lai Yinan（赖一楠），Dai Ye（戴野）

School of Mechanical and Power Engineering，Harbin University of Science and Technology，Harbin 150080，P.R.China

To analyze the attitude errors of vertical docking test system of small satellite，the static error and kinematic error of test system are considered.The working principle of test system and coordinate of actuator are introduced.The model of friction torque on the joints and torque on docking mechanism are built.Dynamics equation of actuator is built by the Lagrange equation and the Nielsen equation.Under the condition of 24 different angle groups，the calculation of dynamics equation is built by using MATLAB/SIMULINK platform and the kinematic errors of actuator are obtained.The attitude error models of docking mechanism are built.Results shows that the main angle error sources of yaw，row，pitch are not identical.The attitude error of yaw angle can be decreased by compensating the angle error around x axis.The attitude error of row angle mainly originates in the system error，and it can be eliminated by adjusting non-orthogonal degree.

attitude error；test system；angle errors；dynamics equation

0 Introduction

Small spacecrafts are widely used in military，remote communication，disaster prediction and other fields［1-2］.On-orbit dock missions for small aircraft are mainly for fuel supplies，transferring sample in deep-space exploration，failed satellite service，aided-mechanism expansion，assistantorbiting for satellite，etc.All these avoid transporting people and large quantities，and fuel transport channel need not have big volume.In terms of reliability，cost and flexibility，small dock mechanism has enough advantages over large dock mechanism in the implementation of small satellite dock missions of small carrying capacity and limited installation space.Researches on small dock mechanism with catching characteristics are carried out by space powers，for instance，European Space Agency（ESA）［3］proposed to study the robotic geostationary orbit restorer.German Aerospace Agency［4］supported researches on experimental servicing satellite. Defense Advanced Research Projects Agency（DARPA）supported a demonstration program for frontend robotics to enable near-term demonstration［5］.

At present，the dock mechanisms can be classified into several types：＂three-jaw＂type，＂mechanical arm＂type，＂cone and pole＂type，etc. Among them，＂three-jaw＂type dock mechanism［6］has the least impact force，the lowest velocity and angular velocity in docking.Based on the developed＂three jaw type＂dock mechanism，a series of work have been done to perform the dynamics simulation of a test system.

In the capture and dock processes of＂three jaw type＂mechanism［7］，the dynamics contact［8］between locking jaws of the active dock mechanism（ADM）and passive dock mechanism（PDM）generates action and reaction forces，which will affect test system and attitude anglethrough dock mechanism.In this paper，the errors of attitude angle for docking mechanism are discussed under the influence of the static error and kinematic error［9］.

1 Composition and Principle of Vertical Dock Test System

The whole vertical dock test system is divided into a passive test system and an active test system.As shown in Fig.1，the passive test system is used to install the PDM，thus realizing the rotation around z axis（yaw），x axis（roll），and y axis（pitch），as well as the vertical motion along y direction.The passive test system is mainly composed of a traction counterweight mechanism，a moving end，a hanger frame，a spherical joint bearing，etc.In the active test system，the ADM realizes horizontal movement along x，z directions.The active test system mainly consists of double-rail mobile mechanism.

Fig.1 Vertical dock test system

Experiment processes are stated as follows. Firstly，ADM and PDM are respectively installed on the counter flange of dock test system.Secondly，according to the initial conditions，the location processes are stated as follows.The balance of vertical displacement is realized by adding or reducing counter weight.The balance of the roll and pitch motion are realized by adjusting angle of spherical joint bearing and controlling rotation of motor to initialize yaw angle and horizontal movement along x，z direction.When initialize settings are finished，test system should be in the passive mode state and three locking jaw should be in opening state completely.Finally，

the process of contact and capture of dock mechanism are completed and dock driven by motor is realized.

2 Dynamics Model of Contact Impact System

Researches［10-12］on space dock dynamics simulation have been carried out at home and abroad，which provide subsequent researches with important reference value.But most of the present related researches are concentrated on Stewart simulation test system［13-14］and dock mechanism of androgynous and peripheral type with differential cushion damping system.The dock process of test system studied in this paper is realized by recombination processes of several degree of freedom motions，which is realized by different motion modules independently.It is known that the joint spherical in Fig.1 plays a crucial role in transferring acting force.Dynamics model of actuator is attempted to be built in this paper.

2.1 Introduction to dock process

The dock process of three-jaw dock mechanism is shown in Fig.2.Before dock，locking jaw 3 is located in envelope zone of PDM.As dock system meets dock initial conditions，threaded rod 5 driven by controlling motor rotates.Thread lifting panel 4 is forced to move down，and three locking jaws simultaneously shift down and close gradually.Meanwhile，the PDM is firmly captured，and attitude deviations are adjusted.Finally，the whole system completes connection locking.

2.2 Coordinate definition of actuator

As illustrated in Fig.3，the actuator is composed of hanger frame 1，mandrel 2，angle ruler 3，flange 4 and spherical joint 5.This mechanism has three rotational degrees of freedom，the ran-ges of which are 0—10°.

Fig.2 Dock process

Fig.3 Coordinate definition of actuator

Ox yz is the static coordinate.The moving coordinate oξηζis fastened to spherical joint.The origin point of the Ox yz coordinate is located at the centre of spherical joint.Theζaxis is along the axes of mandrel.In the initial state，the moving coordinate oξηζcoincides with Oxyz，and the positive direction ofξ，η，ζare the same with x，y，z.

In order to obtain the space position of mechanism，Euler anglesφ，θ，ψare defined as the generalized displacements.First，the mandrel and the hanger frame rotate along z axis and reach the NY1z coordinate.Second，the mandrel rotates along the N axis and reaches the NY2ζcoordinate.Third，the hanger frame rotates alongζ axis and reaches theξηζcoordinate.The coordinate transformation is described as which is simplified by

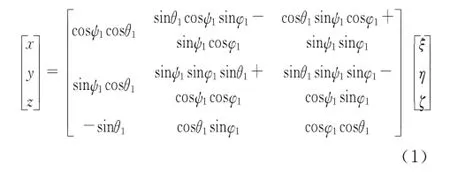
2.3 Friction torque of spherical joint

The normal stress distribution rule of contact surface is

The friction torque is described as

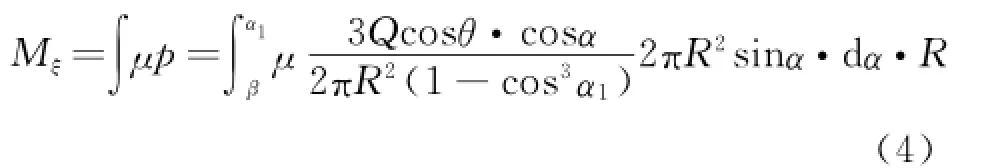
where r is the mandrel radius.Substituteβ= arcsin r/R into Eq.（4）.

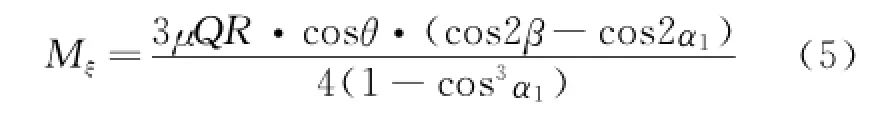
Fig.4 Friction torque of spherical joint

2.4 Contact force and moment

For the three-jaw dock mechanism，when in the test there exists angular deviation relative to static coordinate system，gradually-closing locking jaws firmly grasp passive dock mechanism and adjust posture deviation under the function of three V-type guide grooves.Finally，the lockingjaws slip into the bottom of V-type guide grooves，and PDM is dragged to ADM simultaneously.

The contact type is divided in two parts：（1）turn angle is yaw angleψ，named the front impact；（2）turn angle is roll angleφor pitch angle θ，named the oblique impact.

Fig.5 shows the force analysis of PDM in X＇OZ＇.Fn（n=1，2，3）is the contact force projection over X＇OZ＇，applied by the locking jaw. Fn（n=1，2，3）can be decomposed into the force along groove interface and the force perpendicular to groove interface.

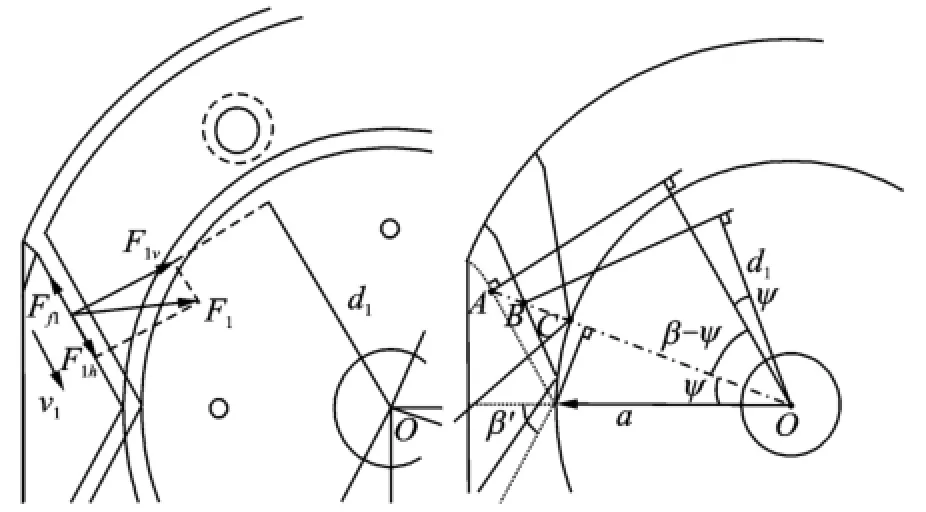
Fig.5 Force analysis and motion trail of locking jaw

As shown in Fig.5，rACis the total displacement of jaw under X＇OY＇coordinate.Assume that after a few seconds，the jaw reaches point B，and the mandrel rotatesΔψangle.v0is the radial velocity of jaw.The torque can be described as

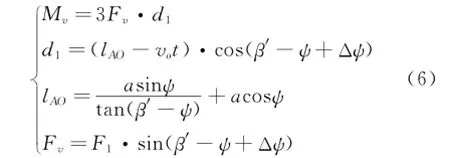
Fn（n=1，2，3）is mainly determined by equivalent stiffness and damping characteristics. Fnandδsatisfy the following equation

where

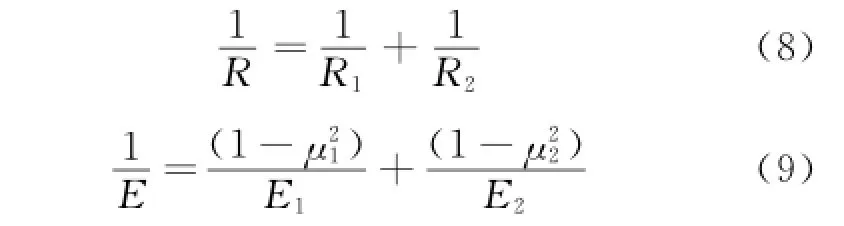
Here，R1，R2are the curvature radii on impact point of two objects；E1，E2the material elasticity moduli；andμ1，μ2the material Poisson ratio respectively.

Impact process is accompanied by energy losses，which is created by damping characteristics. So this paper adopts a model as

where k is the equivalent stiffness，k=1.0×105. δ，.δare the penetration depth and the relative movement speed，respectively.D is the damping parameter and generally it is（ 0.1%—1%）k， here D=100.n is the stiffness contribution index，for metal，n=1.3—1.5，here being 1.5.

2.5 Dynamics model of mandrel and hanger frame

Under the Oξηζcoordinate，the mandrel rotates aroundξaxis.Under the Ox yz coordinate，the mandrel and hanger frame rotate around z axis.Angular displacement is taken as generalized displacement，that is

The torque Mψaroundψaxis includes Mψ1and Mψ2，which act on the hanger frame and the mandrel，respectively.

p，q，r are the projections of absolute angular velocity vectorωof mandrel，which have relationships with generalized velocity.

Jzis the rotational inertia of hanger frame around z axis.A，B，C are the rotational inertias of mandrel aroundξ，η，ζaxes.The kinetic energy T1of hanger frame and T2of mandrel can be described as

The dynamics equation can be obtained by using the Lagrange equation.

T2can be described as

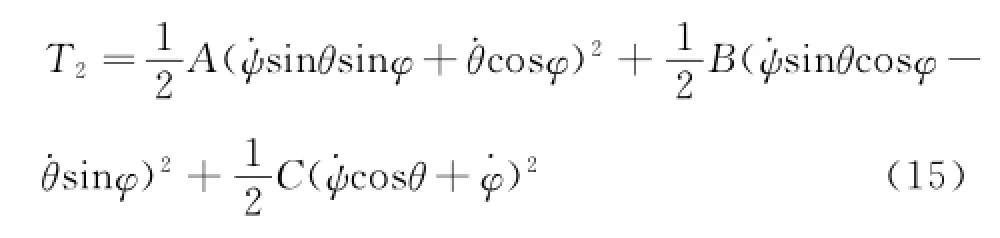
The Nelson equation applied forφ，θ，ψcan be described as

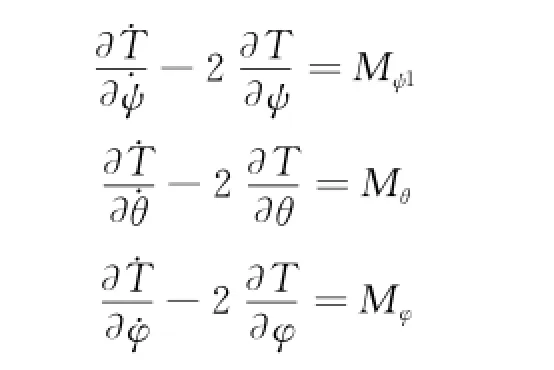
Dynamics differential equations of mandrel are obtained from Eq.（15）.

Define

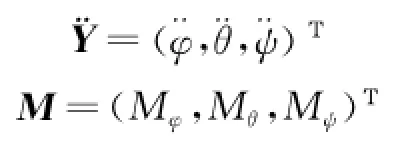
where

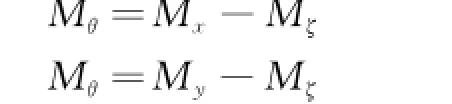
Here，Mx，Myare the torques of PDM applied by the locking jaw.Eq.（16）can be described as

where

3 Simulation Flow

In Eq.（5），μ=0.4，Q=60 N，R=0.04 m，mandrel radius r=0.014 m，α1=π/2.The radial velocity of locking jaw v0=0.001 m/s.The angle of V-type guide groove is 120°.In Eq.（6），a= 260 mm.

In Eq.（13），Jz=3.95 kg·m2，rotational inertias of mandrel is

The simulation model is built by using the MATLAB/SIMULINK platform.In order to obtain the motion errors of different angle，the angles of 24 groups are selected，as shown in Table 1.

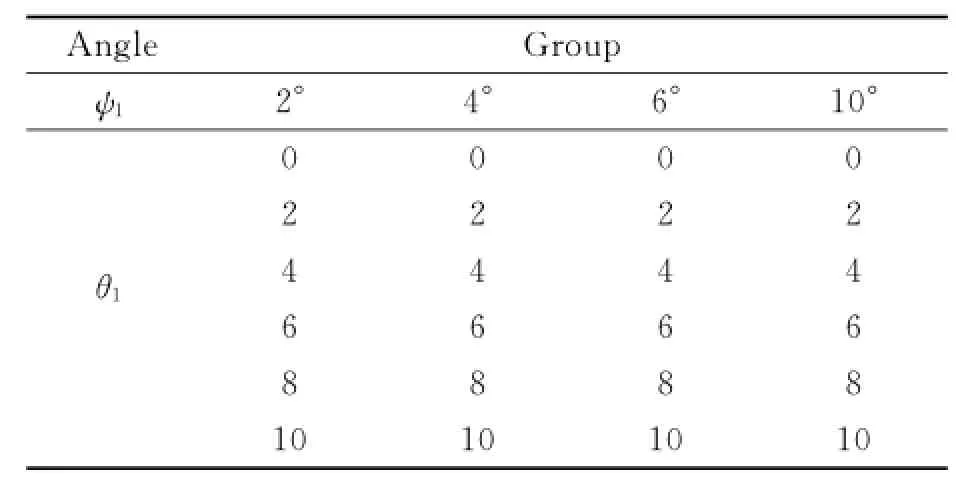
Table 1 Angles of 24 groups （°）

Table 2 shows the simulation results of different angles.

Table 2 Simulation results （°）

4 Error Analysis of Attitude Angle

Fig.6（a）shows the coordinate of gravity center of docking mechanism.Static coordinate Ox＇y＇z＇rotatesγ（yaw），α（row），β（pitch）degrees aroundaxes，respectively to coordinate Ox1y1z1，where the three angles are the corresponding attitude angles.The coordinatetransformation is described as

namely，

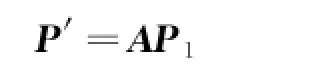
The elements in Eq.（1）are equal to elements in Eq.（18）.

If actuator generates angular error，the attitude angles are

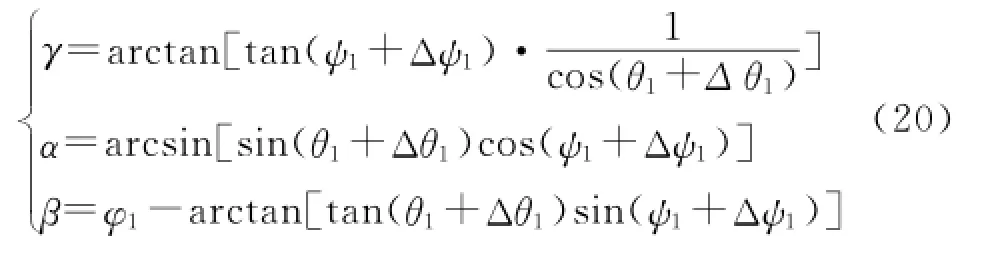
Letφ1=0 sinceφ1does not influence the attitude angle error ranges.

Eq.（20）is the formula to calculate actual attitude angles of docking mechanism under the influence of angular error.In addition，the nonorthogonal degree exists in the coordinate Oxyz caused by normal wear，installation errors，manufacture errors，and so on.As shown in Fig.6（b），the angles between z axis and x，y，z＇axes areπ/2+δ1，δ3，andπ/2+δ2，respectively.

Fig.6 Coordinates

Eq.（21）can be obtained from the first rotation in Fig.3.

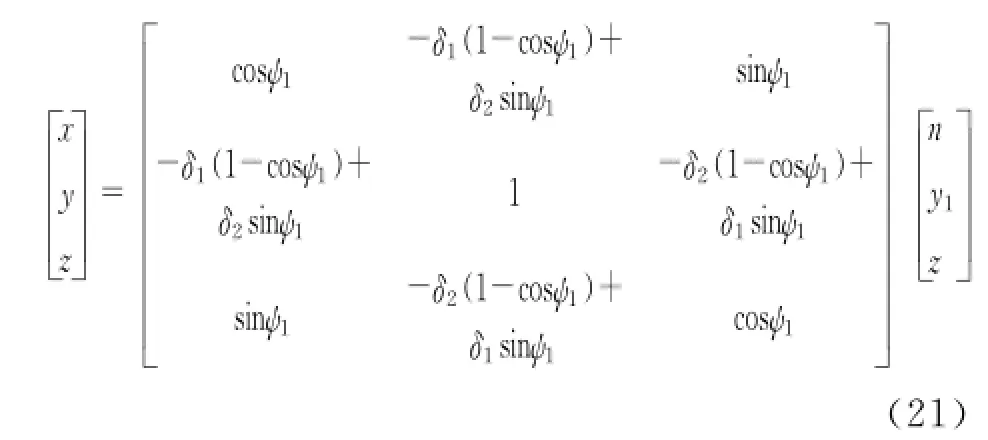
Eq.（22）can be obtained from the simultaneous equations of Eq.（21）with the other two rotation transformational matrixes.

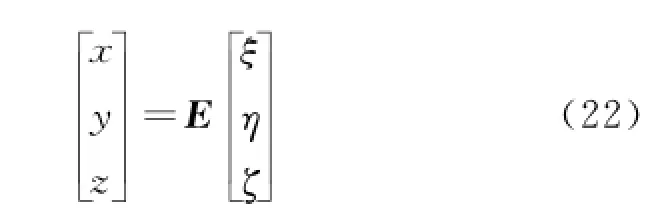
E is the matrix multiplication of the three rotations，whose elements are equal to elements of Eq.（18）.

where

From Eqs.（23），（24），for the givenθ1and ψ1，e1and e2attain the maximum values whenδ1andδ2have the same sign and reach the maximum value（d）of non-orthogonal degree.Thus the attitude angle errors ofγandαare maximized. While e3and e4reach the maximum values when δ1andδ2have the opposite sign，the absolute values are the maximums of non-orthogonal degree. Therefore，the attitude angle error ofβgoes for a maximum value.

The attitude angles can be described as

The maximal attitude angle deviating from a nominal value can be obtained by Eq.（20）and Eq.（25）.The attitude angles can be obtained by taking angle errors into Eq.（26），here d=30＂. Table 3 shows the attitude errors ofγandα. Fig.7 is the plot of the maximal errors ofγ，αand β.

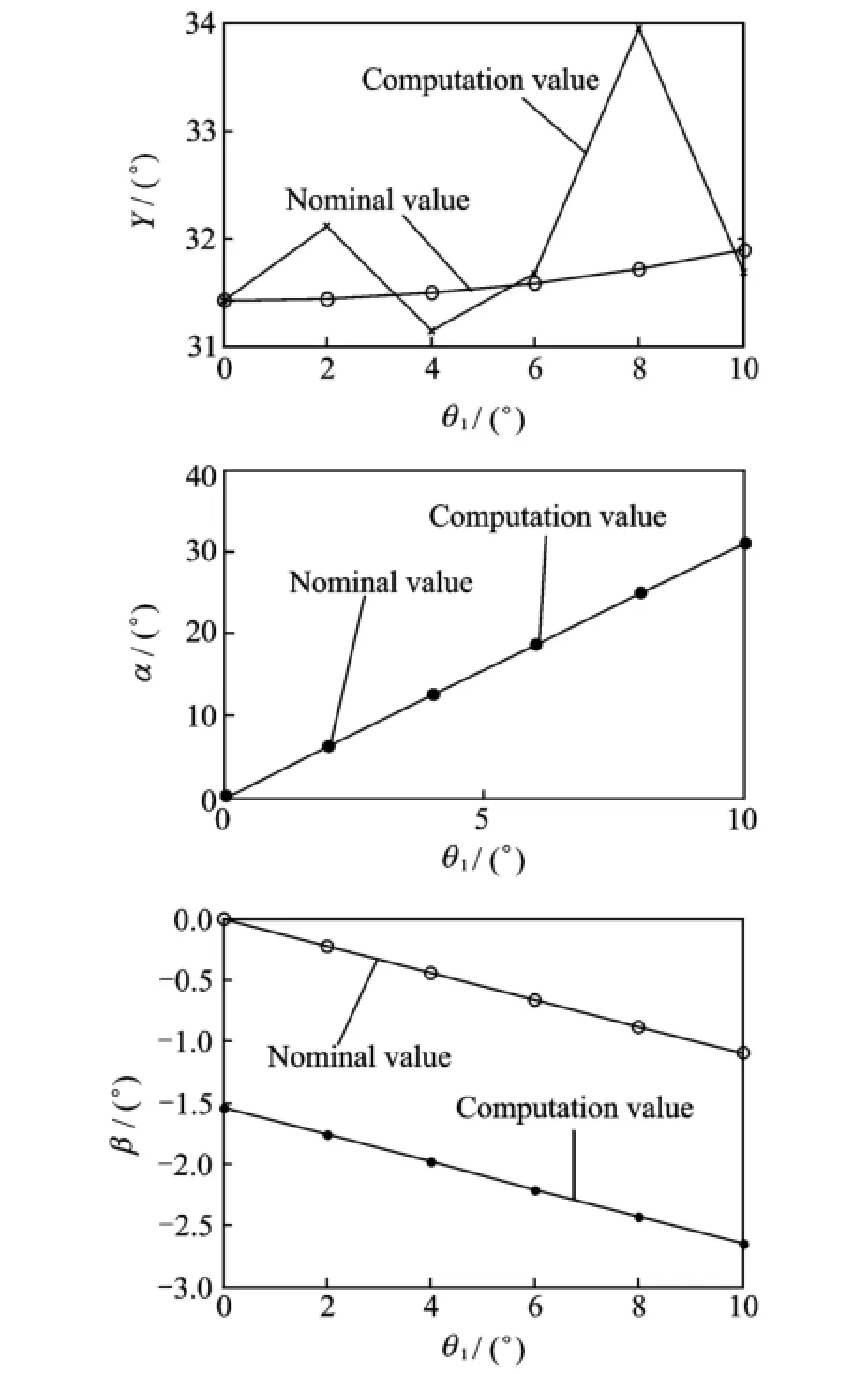
Fig.7 Actual attitude angle

In Table 3，the deviation variation trends of differentψ1values are the same.In Fig.7，with the same non-orthogonal degree，the angle errorsinfluenceγsignificantly.The graph ofγis similar to a sine curve.Whenψ1is given，the deviation of γreaches its maximum atψ1=2°，θ1=8°.The attitude angle errors ofγcan be decreased by compensating the error of angleθ1.The actual value and nominal value ofαare virtually equal，which indicates that the attitude error ofαmainly originates in system error.In this case，ifδ1andδ2can be measured，and the exact value of attitude angle can be obtained，then the system error can be eliminated.The attitude errors ofβare inversely proportional toψ1.Whenψ1=2°，its maximum valueΔβ=1.544 9°is obtained.

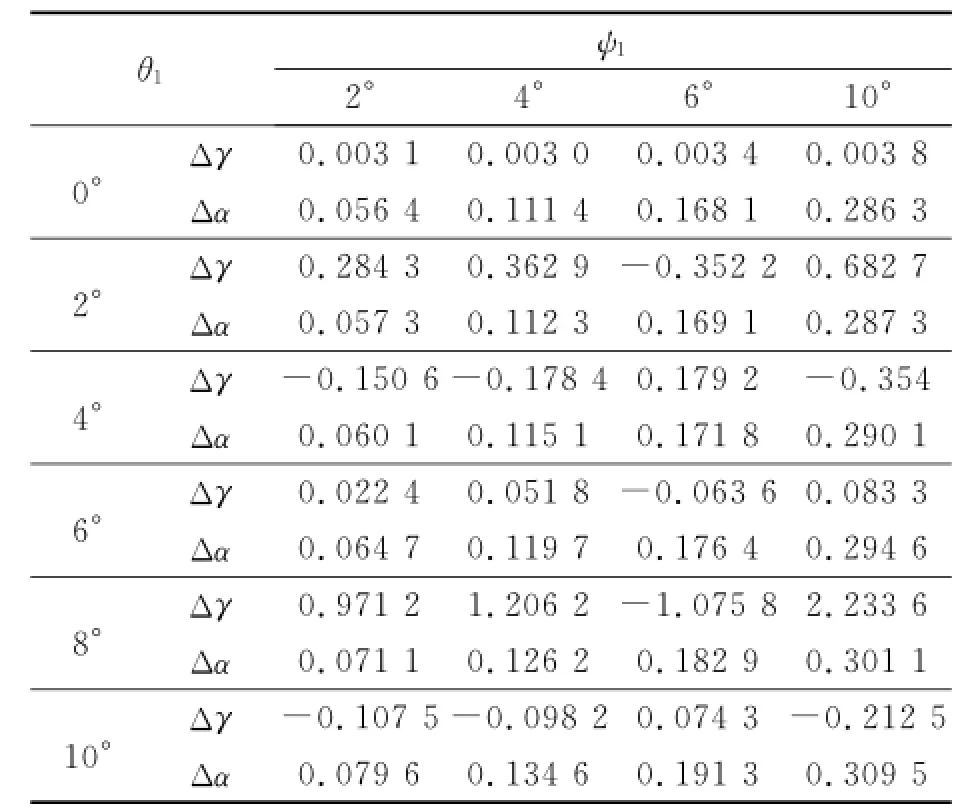
Table 3 Attitude errors （°）

5 Conclusions

According to the work principle of actuator，static coordinate and moving coordinate are introduced.Based on the Herz elastic deformation theory，the model of friction torque on the joints and torque on the docking mechanism are built.Dynamics equation of actuator is obtained by the Lagrange equation and the Nielsen equation.

Dynamics simulation model is developed by using the MATLAB/SIMULINK platform.The attitude error model of docking mechanism is built under the influence of static error and kinematic error.Kinematic errors of actuator are obtained.From the calculation results，main error sources of yaw，row，pitch are not identical.Fi-nally，the methods to reduce the attitude errors are put forward.

Acknowledgements

This work was supported by National Natural Science Foundation of China（No.51375125），the Foundation for Distinguished Young Scholars of Heilongjiang Province，China（No.JC201111），and the Program for New Century Excellent Talents in University（No.NCET10-0146）.

［1］ Ennico K，Shirley M，Colaprete A，et al.The lunar crater observation and sensing satellite（LCROSS）payload development and performance in flight［J］. Space Science Reviews，2012，167（1/2/3/4）：1-47.

［2］ Bhatia A，Goehner K，Sand J，et al.Sensor and computing resource management for a small satellite［C］∥Aerospace Conference，2013 IEEE.［S.l.］：IEEE，2013：1-8.

［3］ ESA.Robotic geostationary orbit restorer［EB/OL］. http：∥www.esa.int/TEC/Robotics/SEMTWLKK KSE.html.［2010-04-03］.

［4］ Hirzinger G，Landzettel K，Brunner B，et al.DLR＇s robotics technologies for on orbit servicing［J］.Advanced Robotics，2004，18：139-174.

［5］ DARPA Tactical Technology Office.Front-end robotic enabling near term demonstrations project page［EB/OL］.http：∥www.darpa.mil/tto/programs/ frend.htm.［2010-04-03］.

［6］ Zhang Y，Wang J，Song Y，et al.Dynamic simulation analysis for docking mechanism of on-orbit-servicing satellite［J］.Applied Mechanics and Materials，2014，487：313-318.

［7］ Zhao M J.Key technical study of ground six degrees of freedom platform for microsatellite docking mechanism［D］.Harbin，China：Harbin University of Science and Technology，2011：5-30.（in Chinese）

［8］ Xu C L，Wang X W.Efficient numerical method for dynamic analysis of flexible rod hit by rigid ball［J］. Transactions of Nanjing University of Aeronautics& Astronautics，2012，29（4）：338-344.

［9］ Zhao H S.Model of flight technical error in symmetrical plane for performance based navigation［J］. Transactions of Nanjing University of Aeronautics& Astronautics，2011，28（3）：246-254.

［10］Li C G，Wang H M，Zhu J Y.Dynamics analysis of 2-DOF spherical parallel mechanism［J］.Transactions of Nanjing University of Aeronautics&Astronautics，2009，26（2）：95-100.

［11］Howsman T G，Glaese J R.Space station docking mechanism dynamic testing［J］.Space Science Reviews，2008，89（12）：168-175.

［12］Shi J W.Study on 6-DOF simulator dynamics for half-physical synthetic docking simulation precision［D］.Shanghai，China：Shanghai Jiaotong University，2012：29-40.（in Chinese）

［13］Dasgupta B，Mruthyunjaya T S.Closed-form dynamic equations of the general Stewart platform through the Newton-Euler approach［J］.Mechanism and Machine Theory，1998，33（7）：993-1012.

［14］Colebank J E，Jones R D，Pollak R D，et al.SIMSAT：A satellite system simulator and experimental test bed for air force research［R］.Simsat A Satellite System Simulator&Experimental Test Bed for Air Force Research，1999.

（Executive editor：Zhang Tong）

V216.8 Document code：A Article ID：1005-1120（2015）04-0372-08

*Corresponding author：Zhang Yuan，Professor，E-mail：zhangyuan1966@163.com.

How to cite this article：Zhang Yuan，Sun Lili，Lai Yinan，et al.Dynamics and attitude error analysis for dock test system of small satellite［J］.Trans.Nanjing U.Aero.Astro.，2015，32（4）：372-379.

http：//dx.doi.org/10.16356/j.1005-1120.2015.04.372

（Received 27 February 2014；revised 19 April 2014；accepted 24 April 2014）