A New Regularized Minimum Error Thresholding Method

Wang Baoping（王保平），Zhang Yan（张研），Wang Xiaotian（王晓田），Wu Chengmao（吴成茂）

A New Regularized Minimum Error Thresholding Method

Wang Baoping（王保平）1*，Zhang Yan（张研），Wang Xiaotian（王晓田）1，Wu Chengmao（吴成茂）2

1.National Key Laboratory of Science and Technology on UAV，Northwestern Polytechnical University，Xi＇an 710072，P.R.China；2.School of Electronics Engineering，Xi＇an University of Posts and Telecommunications，Xi＇an 710121，P.R.China

To overcome the shortcoming that the traditional minimum error threshold method can obtain satisfactory image segmentation results only when the object and background of the image strictly obey a certain type of probability distribution，one proposes the regularized minimum error threshold method and treats the traditional minimum error threshold method as its special case.Then one constructs the discrete probability distribution by using the separation between segmentation threshold and the average gray-scale values of the object and background of the image so as to compute the information energy of the probability distribution.The impact of the regularized parameter selection on the optimal segmentation threshold of the regularized minimum error threshold method is investigated.To verify the effectiveness of the proposed regularized minimum error threshold method，one selects typical grey-scale images and performs segmentation tests.The segmentation results obtained by the regularized minimum error threshold method are compared with those obtained with the traditional minimum error threshold method.The segmentation results and their analysis show that the regularized minimum error threshold method is feasible and produces more satisfactory segmentation results than the minimum error threshold method.It does not exert much impact on object acquisition in case of the addition of a certain noise to an image.Therefore，the method can meet the requirements for extracting a real object in the noisy environment.

image processing；image segmentation；regularized minimum error threshold method；informational divergence；segmentation threshold

0 Introduction

It is difficult for computer vision to analyze，understand and segment an image.Among the many image segmentation methods，the threshold segmentation method is extensively studied and applied due to its simplicity，rapidity，effectiveness，stability and ease of understanding［1］.The minimum error threshold method［2］is applied the most extensively among image segmentation methods because of its firm support by the probability theory.Kittler and Illingworth，the proponents of the method，obtained the threshold segmentation criteria with the Bayesian error theory and some reasonable mathematical treatments on the assumption that the gray scale distributions of ideal objects and backgrounds obey the mixed normal distribution.Many scholars at home and abroad studied the minimum error threshold method［3-10］，for instance，the fast iteration algorithm［3］，the robust minimum error threshold method［4］，the Poisson distribution minimum error threshold method［6］，the Rayleigh distribution minimum error threshold method［7］，the generalized minimum error threshold method［8］and so on.In order to enhance the noise resistance of the minimum error threshold method，they proposed the 2D histogram minimum error threshold method［9］and its fast algorithm［10-12］.To reveal the theoretical foundation of the method more clearly，Refs.［13-14］used informational divergence to give a reasonable explanation to the minimum er-ror threshold segmentation method，thereby laying a firm theoretical foundation for using the method better.Since the minimum error threshold method is derived from pattern matching，the distribution of the gray scales of the object and background of its hypothetical image strictly obeys the mixed normal distribution，the Poisson distribution，the Rayleigh distribution，etc. However，because of the acquisition environment and transmission interference of an actual image，the distribution of its gray scales cannot strictly obey the mixed normal distribution，the Poisson distribution，the Rayleigh distribution，etc.The thresholds segmented with the minimum error threshold method are not necessarily the ideal ones required by image segmentation，causing severe segmentation errors.To reduce the image segmentation error rate of the minimum error threshold segmentation method，a regularized minimum error threshold method is proposed so as to enhance its segmentation performance，while treating the traditional minimum error threshold method as the former＇s special case.

1 Minimum Error Threshold Method

Use f（x，y）to denote the gray value of an arbitrary pixel located at（x，y）of a digital image whose size is M×N.The one-dimensional（1D）histogram of the image h（i）denotes the frequency number at which all the gray-scale values of the image appear.Therefore，one can use the 1D histogram to describe the image＇s probability distribution.

Kittler and Illingworth［2］gave the following expression based on the minimum segmentation error

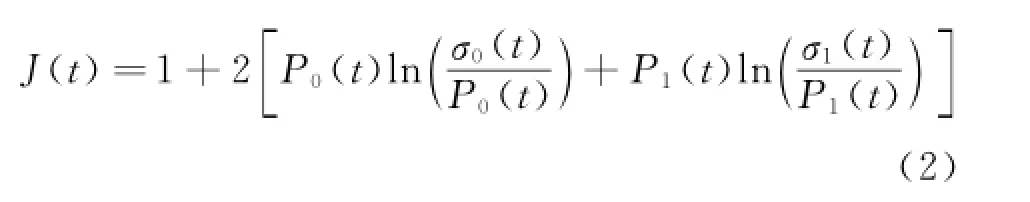
The criterion for selecting the best segmentation threshold value is t=t*that minimizes J（t），namely

To have a profound understanding of the minimum error threshold method，Refs.［13-14］minimize the informational divergence between the actual distribution h（l）and the hypothetical distribution p（l）and derive the expression again，further clarifying the mathematical mechanism of the method.

The divergence of the parametricalαbetween the two discrete probability distributions P=（p1，p2，…，pn） and Q=（q1，q2，…，qn） is as follows

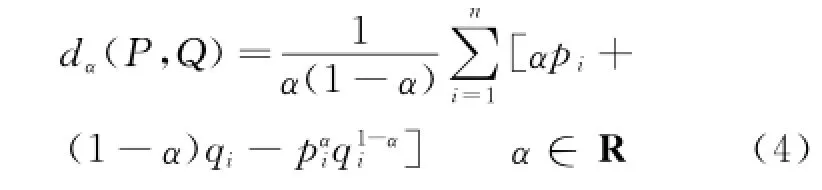
The divergence of the parametricalαhas the following characteristics：

（1）dα（P，Q）is concerned with P，Q and is a concave function；

（2）dα（P，Q）≥0；when and only when P= Q，dα（P，Q）=0；

（3）The divergences of KL andχ2are the special cases ofα-type divergence，namely

which is the famous KL divergence.Also

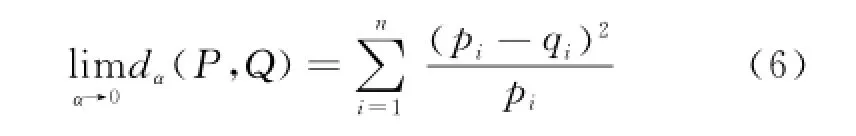
which is the classicχ2divergence.

The minimum error threshold method can be explained with the KL divergence as

This explanation demonstrates that the minimum error threshold method is，in nature，the gray-scale normal distribution template matching method.

2 Information Entropy and Energy

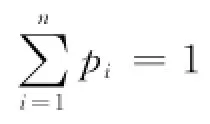
The information entropy has the following typical properties：

（1）If∀i∈｛1，2，…，n｝and pi=1/n，the information entropy H（P）reaches the maximum value ln（n）；

（2）If∃i∈｛1，2，…，n｝an d pi=1，the information entropy H（P）reaches the minimum value 0.

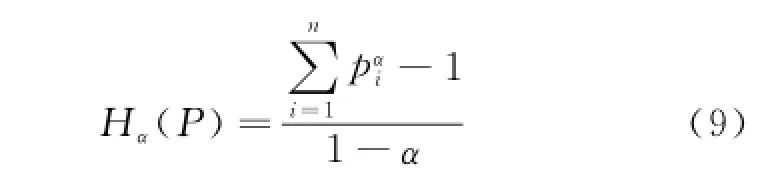
where is the discrete uniform probability distribution.

The parametric-type expression of information entropy has the following properties：

（1）If the parameterα→1，then

（

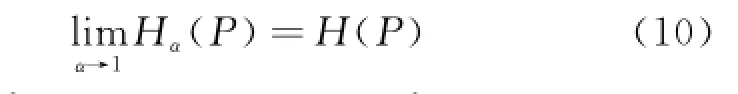
2）If the parameterα=2，then

（3）If the probability distributions of any two independent events A and B are P1and P2，then

（1）If∀i∈｛1，2，…，n｝and pi=1/n，the information energy E（P）reaches the minimum value 1/n；

（2）If∃i∈｛1，2，…，n｝an d pi=1，the information energy E（P）reaches the maximum value 1.

From the above definitions，one can see that the information entropy and the information energy are in pairs.In particular，H2（P）and E（P）satisfy the validity of H2（P）=1-E（P），so that information energy is related to divergence dα（P，Q）as follows

This expression provides the possibility of combining information energy with the minimum error threshold criteria.

3 Regularized Minimum Error Threshold Method Based on Informational Divergence

Since the threshold segmentation method is a special type of clustering segmentation method which，however，has uncertainty，the regularization theory has been applied to the study of clustering algorithm［18-19］so as to enhance its performance.The informational divergence theory has also been extensively studied in the construction of the clustering algorithm［20］，whose generalized clustering model has been established.The regularization theory has been applied to the improvement of the Otsu threshold method，thus obtaining the improved global threshold segmentation method for fused image gray-scale contrast［21］and the regularized parameter selection method.Saha et al.［22］proposed the regularization variance minimum and maximum local threshold segmentation method and worked out the method for adaptively selecting regularization parameters.To segment an image，one develops the regularized minimum error threshold method based on informational divergence by combining the information energy of object and background of the image with the informational divergence that corresponds to the template matching method.

3.1 Construction of regular items with information energy

It is assumed that an image has the L gray level G=｛0，1，2，…，L-1｝ and its histogram is h（i）（i=0，1，…，L-1）.Given that its segmentation threshold is t（0＜t＜L-1），one segments the image into object and background，each of which corresponds to the following average gray scales

where P0（t）and P1（t）are a posteriori probability values that correspond to object and background respectively.

With the weighted Otsu threshold coefficient constructed in Ref.［23］，one uses the segmentation threshold t，the average gray-scale value of the object m0（t）and the average gray-scale value of the background m1（t）to construct the discrete probability distribution as follows：

The discrete probability distribution P＇：（p＇1p＇2），where

The information energy possessed by the discrete probability distribution P＇is

The value of information energy increases with increasing deviation between the segmentation threshold and the average gray-scale values of the object and background respectively.On the contrary，the value of information energy decreases with decreasing deviation between the segmentation threshold and the average gray-scale values of the object and background respectively.

3.2 Regularized informational divergence threshold method based on information energy

Under the condition that the segmentation threshold t（0＜t＜L-1）is given，the probability that corresponds to any gray scale i（i=0，1，…，L-1）is h（i）（i=0，1，…，L-1）.

The minimization of the deviation betweenthe probability and the joint normal probability distribution of the object and background with the assumed ideal normal distribution constitutes the minimum error threshold criteria.One uses the separate information energy between object and background to construct the regularized informational divergence threshold method，namely

In Eq.（16），the selection of the regularized factorλis of great importance for obtaining the ideal segmentation threshold.The value of the parameterλmay be positive or negative，and its symbol can be determined with the method to be presented in Section 4.

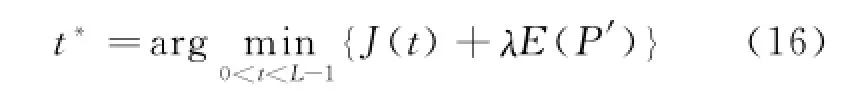
4 Method for Selecting Symbol of Regularized Parameter

If the object deviation and the background deviation that correspond to a given segmentation valueareand；and if-is larger than 0，the parameterλis selected as a positive symbol；ifis smaller than 0，the parameterλis selected as a negative symbol；ifis equal to 0，the parameterλis selected as 0.

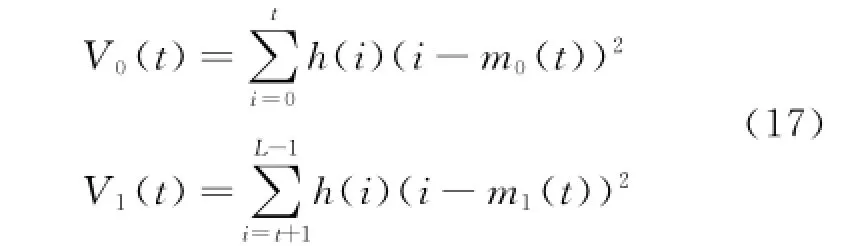
where the criterion for selecting the parameter t*2is

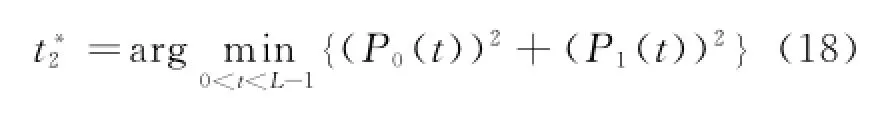
5 Explanation on Rationality of Regularized Minimum Error Threshold Method

Assuming that the probability of the image＇s histogram is a continuous function h（x），one constructs the objective function that corresponds to the regularized minimum error threshold criteria as follows

Accordingly，one obtains the derivative of J（t）with the segmentation threshold t as follows

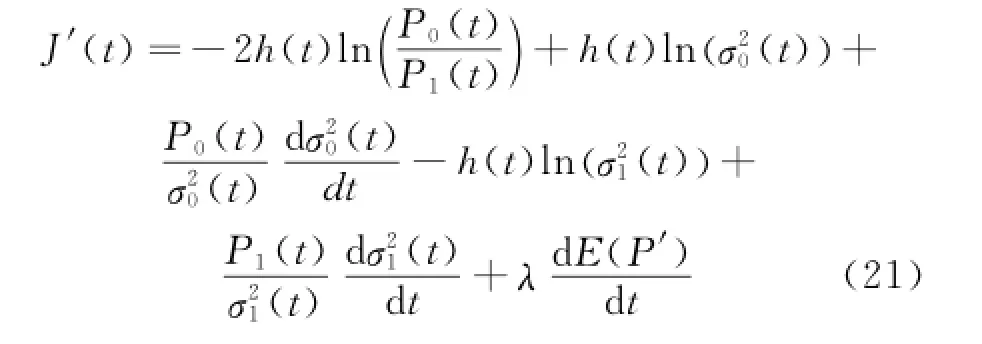
where

If its derivative is J＇（t）=0，one can obtain the iteration expression for acquiring the segmentation threshold

where

where E＇（P＇）is the derivative of E（P＇）to the parameter t.

Since the probability distribution of the histogram of an actual image is discrete and its integral can be discretely and approximately summed rather than calculated，the discrete iteration formula that corresponds to the regularized minimum error threshold method can be obtained，whereas the discrete iteration formula that corresponds to the traditional minimum error threshold method is

Therefore，the regularized minimum error threshold method，in nature，is to add the threshold obtained with the traditional minimum error threshold method to the allowance E＇（P＇）/g2（t（k））controlled by the parameterλso that the obtained segmentation threshold will be more approximate to the ideal segmentation threshold of the image itself，thus reducing the image’s segmentation error rate.

The above analysis shows that the regularized minimum error threshold method，in nature，corrects the segmentation threshold obtained with the traditional minimum error threshold method and treats the latter as a special case of the former.

6 Experiments and Result Analysis

To verify the effectiveness of our regularized minimum error threshold method based on informational divergence，one selects some typical grey-scale images and carries out the test analysis of the images obtained with our regularized minimum error threshold method and the traditional minimum error threshold method respectively.

6.1 Parameter selection and test

The regularized parameterλis important for the regularized minimum error threshold method. The selection of inappropriate parameters may cause immeasurable loss to the subsequent image processing.Therefore，one investigates the impact of the regularized parameter selection on the optimal segmentation threshold of the regularized minimum error threshold method.

One uses the four standard gray-scale images，i.e.，Lena，cameraman，mug and the moon（Fig.1）to investigate the impact of the regularized parameterλof the regularized minimum error threshold method on its segmentation threshold. The image segmentation results are presented in Table 1.The regularized parameter isλ=4γ，whose symbol uses the object and background a posteriori probability information energy minimum determination method.

Fig.1 Raw images

Table 1 Image segmentation results on four images

The segmentation results on the four images（Table 1）show that，if the absolute value of the parametricγin the regularized parameterλtakes 0，the regularized minimum error thresholding method proposed in this paper may function the same as the classic minimum error thresholding method，whose optimal threshold for segmenting a gray image is the smallest.As the absolute value of the parametricγin the regularized parameter λincreases gradually，the optimal threshold of the gray image segmented by the regularized minimum error threshold method changes monotonously.When the parameter|γ|is greater than 2，the optimal threshold of gray image does not change obviously.In general，if the absolute value of the parametricγin the regularized parameter λin the majority of grey-scale images is less than or equals to 1，satisfactory segmentation results are obtained.But if the ratio of mean value to variation of gray image is greater than the constant of 0.05，the parametric absolute valueγin the regularized parameterλmust be 2 in order to obtain better segmentation quality.

6.2 Image segmentation result comparison

The gray-level image segmentation results，given in Fig.2，and their analysis show that the regularized minimum error threshold method is feasible and produces more satisfactory segmenta-tion results than the minimum error threshold method.

Fig.2 Result comparison between the regularized minimum error threshold method and the minimum error threshold method

6.3 Robutness test of the regularized minimum error threshold method

To test robustness of the regularized minimum error threshold method，one compares the results of segmenting the standard images of Lena and cameraman respectively.The segmentation results are given in Figs.3，4.The mean value of the image with the Gaussian noise is 0，and its standard deviations are 0，8.0，16.0，and 25.5，respectively.

Fig.3 Segmentation results on image of Lena with the Gaussian noise mean value as 0

Fig.4 Segmentation results on image of a cameraman with the Gaussian noise mean value as 0

The image segmentation results，given in Figs.3，4，and their analysis show that，compared with the traditional minimum error threshold method，the regularized minimum error thresholdmethod does not exert much impact on object acquisition in case of the addition of a certain noise to an image.However，the traditional minimum error threshold method is quite sensitive to noise and cannot acquire the precise information on its object when the noise is large.Therefore，the proposed method can meet the requirements for extracting a real object in the noisy environment.

7 Conclusions

The uncertainty-reducing regularization theory is introduced into the study of the image segmentation with the minimum error threshold method and a new regularized minimum error threshold method is proposed to solve the degree of separation between the segmented object and the segmented background，where the traditional minimum error threshold method is not taken into account.The new method treats the traditional minimum error threshold method as its special case and can enhance the segmentation performance of the latter.Besides，the regularized minimum error threshold method can be extended to the scenarios with multiple threshold values and other various minimum error threshold methods so long as the object and background in the image obey the Poisson distribution or the Rayleigh distribution.

Acknowledgements

This work was supported by the National Natural Science Foundations of China（Nos.61136002，61472324）and the Natural Science Foundation of Shanxi Province（No.2014JM8331）.

［1］ Sezgin M，Sankur B.Survey over image threshold techniques and quantitative performance evaluation［J］.Journal of Electronic Image，2004，13（1）：145-165.

［2］ Kittler J，Illingworth J.Minimum error threshold［J］.Pattern Recognition，1986，19（1）：41-47.

［3］ Ye Q Z，Danielsson P E.On minimum error threshold and its implementations［J］.Pattern Recognition Letters，1988，7（4）：201-206.

［4］ Cho S，Haralick R，Yi S K.Improvement of Kittler and Illingworth＇s minimum error threshold［J］.Pattern Recognition，1989，22（5）：609-617.

［5］ Morii F.A note on minimum error threshold［J］. Pattern Recognition Letters，1991，12（6）：3493-51.

［6］ Pal N R，Pal S K.Image model，Poisson distribution and object extraction［J］.International Journal of Pattern Recognition Artificial Intelligence，1991，5（3）：439-483.

［7］ Xue J H，Zhang Y J，Lin X G.Rayleigh-distribution based minimum error threshold for SAR images［J］. Journal of Electronics，1999，16（4）：336-342.（in Chinese）

［8］ Moser G，Serpico S B.Generalized minimum-error threshold for unsupervised change detection from SAR amplitude imagery［J］.IEEE Trans Geoscience and Remote Sensing，2006，44（10）：2972-2982.

［9］ Fan J L，Lei B.Two-dimensional extension of minimum error threshold segmentation method for graylevel images［J］.Acta Automatica Sinica，2009，35（4）：386-393.

［10］Fan J L，Lei B.Two-dimensional and linear minimum error threshold segmentation method［J］. Journal of Electronics and Information，2009，31（8）：1801-1806.

［11］Zhu Q D，Jing L Q，Bi R S，et al.Improvement algorithm of minimum-error threshold segmentation method［J］.Opto-Electronics Engineering，2010，37（7）：107-113.

［12］Long J W，Shen X J，Chen H P.Adaptive minimum error threshold algorithm［J］.Acta Automatica Sinica，2012，38（7）：1134-1144.

［13］Fan J L，Xie W X.Minimum error threshold：A note［J］.Pattern Recognition Letters，1997，18（8）：705-709.

［14］Fan J L.Notes on Poisson distribution-based minimum error threshold［J］.Pattern Recognition Letters，1998，19（5/6）：425-431.

［15］Shannon C E.A mathematical theory of communication［J］.Bell System Technical Journal，1948，27：379-423，623-656.

［16］Plastino A，Plastino A R.Tsallis entropy and Jaynes＇information theory formalism［J］.Brazilian Journal of Physics，1999，29（1）：50-60.

［17］Onicescu O.Energic informationnelle（ser A）［M］. Paris：C R Acad Sci，1966：841-842.

［18］Zhang Z H，Zheng N J，Shi G.Maximum-entropy clustering algorithm and its global convergence analysis［J］.Science in China（Series E），2001，31（1）：59-70.

［19］Yu J，Yang M S.A generalized fuzzy clustering regularization model with optimality tests and model complexity analysis［J］.IEEE Trans Fuzzy Systems，2007，15（5）：904-915.

［20］Banerjee A，Merugu S，Dhillon I，et al.Clustering with Bregman divergences［J］.Journal of Machine Learning Researcher，2005，6：1705-1749.

［21］Qiao Y，Hu Q M，Qian G Y，et al.Threshold based on variance and intensity contrast［J］.Pattern Recognition，2007，40：596-608.

［22］Saha B N，Ray N.Image threshold by variational minimax optimization［J］.Pattern Recognition，2009，42：843-856.

［23］Morii F.An image threshold method using a minimum weighted squared-distortion criterion［J］.Pattern Recognition，1995，28（7）：1063-1071.

（Executive editor：Zhang Tong）

TP391 Document code：A Article ID：1005-1120（2015）04-0355-10

*Corresponding author：Wang Baoping，Professor，E-mail：wbpluo@sina.com.

How to cite this article：Wang Baoping，Zhang Yan，Wang Xiaotian，et al.A new regularized minimum error thresholding method［J］.Trans.Nanjing U.Aero.Astro.，2015，32（4）：355-364.

http：//dx.doi.org/10.16356/j.1005-1120.2015.04.355

（Received 16 December 2014；revised 11 May 2015；accepted 19 May 2015）