起伏地形下二维密度反演成像的研究及应用

连伟章赵承宝

（1.成都理工大学地球物理学院，四川成都 610059；2.中国石油天然气管道工程有限公司，河北廊坊 065000）

起伏地形下二维密度反演成像的研究及应用

连伟章1赵承宝2

（1.成都理工大学地球物理学院，四川成都 610059；2.中国石油天然气管道工程有限公司，河北廊坊 065000）

同其它物探反演方法一样，重力反演也存在多解性，尤其在起伏地形下，根据异常分布进行反演的难度较大。重力勘探的前提条件是，研究对象与围岩存在着密度差，去掉观测值中与研究对象无关的影响，就可以获得单纯由研究对象引起的重力异常。本文用水平圆柱体作为理论模型，并用等效源法在起伏地形下进行二维密度反演，主要模拟地形为山脊，并且运用实际资料进行验证，取得了较好的效果。

反演 等效源 起伏地形 重力异常

1 引言

反演就是根据获得的异特征、数值大小、分布情况，结合物性资料来获得地下地质体的形状和空间位置。和其他地球物理反演问题一样，重力反演的解也存在非唯一性，特别在起伏地形下，反演就更加困难。如果不改变包含在引力等位面内的物质总量，而重新分布其密度，使原来的等位面大小和形状保持不变，那么在这一等位面上和等位面外的引力场不会发生变化［1］。在位场理论中，场和场源具有唯一的对应关系，但实际观测得到的重力场只是整个场的一部分，再加上观测误差和随机干扰，使其对观测值的解释不可避免地出现多解性，即有多种可能的场源分布与观测场在一定的误差范围内对应。与观测场对应的场源如果不是真正的场源，我们称它为等效源［2］。冯敬英，煕周襄（1987）提出了将等效源法运用于位场反演［3］，Emila（1973）提出了利用偶极线作为等效源进行磁异常向上和向下延拓以及计算一阶、二阶垂向导数和振幅谱的方法［4］。在其它反演方法中，多解性造成解译的困难，这里利用多解性来对位场进行反演，用等效源的质量分布成像，以突出有用信息，增加解释手段。

2 等效源反演方法的基本原理

图1 模型体的理论异常图

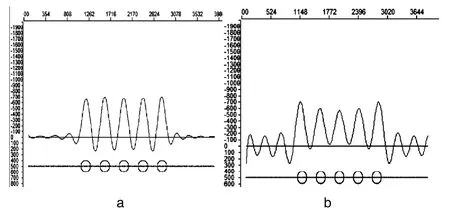
图2 质量分布图

与观测场对应的多个场源中，选择一组最简单的场源，例如按一定位置分布或不固定位置的点荷、线荷，使它们产生的场值在观测面上与实测获得的场值一致，利用这组等效源就可以很方便的做各种位场转换。等效源法的特点可以归纳如下：（1）把各种繁杂的位场转换，变成一个简单的正演计算，计算过程简单，便于统一处理；（2）不丢掉边部测点，条件好的情况下，可以适当外推；（3）对地形起伏较大的观测面，作位场转换的效果仍然较好；（4）由于等效源产生的场仅在观测面内与真实场源产生的场在一定误差范围内吻合，因而用等效源进行位场转换，特别是向下延拓就必然只限于一定的范围内，而不是整个空间，这就是该法的局限性。

在重力反演中，通常我们一般选用模型体的埋深、产状、大小、物性参数等作为最优化反演参量，当用多体模型时需要考虑的参量更多，这时参量太多，计算复杂，多解性也突出［5］。而且在地下地质体很复杂时，往往需要取几个简单的模型体或直接取一个复杂的模型拟合该场源，这种情况下往往很难选到合适的模型体，如果没有选到能适合的初始模型，会导致最后的结果有较大的误差甚至是错误［6］。考虑到等效源可以将复杂模型简单化，因而考虑在重力反演成像中利用等效源进行反演，减少一部分由模型选择带来的误差，简化计算过程，并且根据等效源质量分布图来直观反映地下密度体的情况［7］。

用等效源进行反演成像时主要有以下几个步骤：

（1）根据实际重力异常，初步推测产生异常的地质体的大致范围，并在这个范围内选择一定数量的等效源；（2）设置每个等效源的初始参量作为初值，由于等效源选取得很简单，所以参量也相应变得简单；（3）用最优化方法进行迭代，计算出每个等效源的质量；（4）根据求得的等效源的质量及其分布，用软件作出等效源质量分布图，直观反映场源的情况。

其中，求取等效源是等效源反演中的关键，下面将着重介绍等效源的求取方法。以水平圆柱体作为等效源模型为例，第i个等效源产生在第k个观测点上的重力值为：

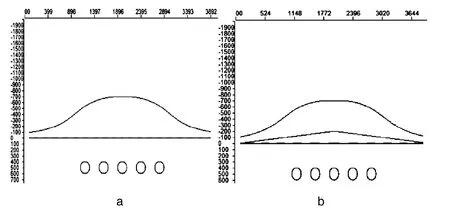
图3 异常曲线图

图4 质量分布图

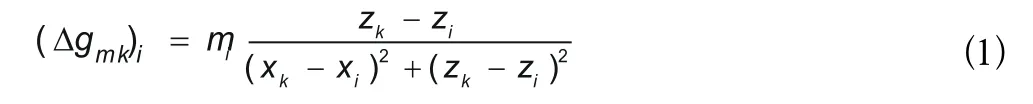
其中，（Δgmk）i表示第 i个等效源产生在第 k个观测点上的引力场垂直分量； mi为第 i个等效源的质量； R为等效源到地质体距离；（xi，zi）为等效源的中心坐标，（xk，zk）为观测点坐标，（i=1，2，…，n，k=1，2，…m）；共有n个等效源，m个观测点，通常m≥n。

令：

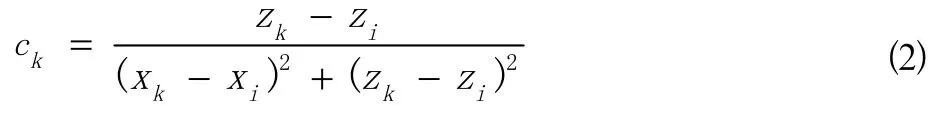
则式（1-1）简记为：

按照场的叠加原理，第k个观测点上的引力场垂直分量应为所有等效源产生在该点上的场值之累加求和，即为：

按等效源的定义，等效源产生在观测点上的场值应与观测值相同，设实测值为g0，即已知测点有m个，可列出m个方程式如下：

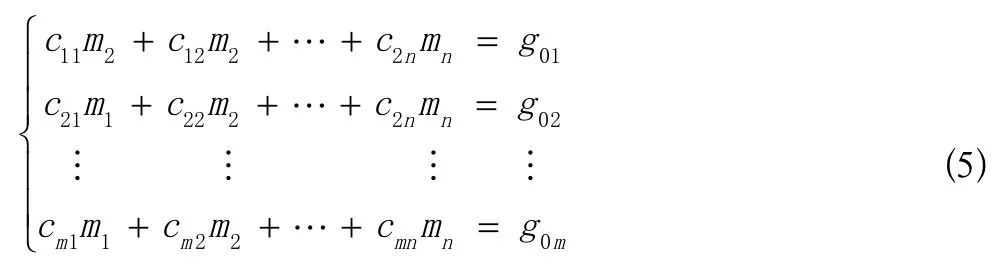
上述方程组未知数为m1，m2…mn共n个，而方程式有m个，因mn，所以为一超定方程组，一般求其最小二乘意义下的近似解，即目标函数 Φ为极小的解m1，m2…mn。

从而归结为求解多元函数的极值问题。这里我们采用解病态方程组效果较好的奇异值分解法直接求解式（3），从而得到等效源参量分布。

3 理论模型

对于一些截面接近圆形并且在水平方向上延伸比较长，如扁豆壮矿体、两翼较陡的长轴向斜和背斜研究它们的异常时，在一定误差范围内，可以把它们当成水平圆柱体。对于无限长水平圆柱体引起的异常，完全可以当作剩余质量集中在中轴线上的物质线看待［8］。本文就用水平圆柱体作为理论模型。在水平地形下设计五个大小一致，埋深相同，密度均匀分布的水平圆柱体作为将要反演密度体的理论模型。模拟水平地形水平圆柱体的中轴线x、z坐标分别为（500，1200）、（500，1600）、（500，2000）、（500，2400）、（500，2800），模拟山脊水平圆柱体的中轴线x、z坐标分别为（500，1200）、（500，1600）、（500，2000）、（500，2400）、（500，2800），半径均为100，相对围岩的密度差都为-2.67g/cm3。

首先正演出五个模型体的理论异常如图1，a为模拟水平地形，b为山脊地形。由图1可知：由于水平圆柱体质检的距离较小，各个圆柱体的异常相互叠加，从整个异常曲线辨别是哪种模型引起的异常。根据此异常分布很难给出模型的个数及反演参数的初值。我们根据理论异常做等效源反演。

首先，在深度为500，x为0-4000的范围内，从0开始以20为间隔设计201个等效源。用SVD解方程求出等效源的质量分布，画出质量分布图2，a为水平地形，b为山脊地形。由图2看出，等效源质量分布位置与理论模型的位置相吻合。根据等效源的质量分布，做出异常曲线图3，可以看出与模型产生的异常曲线一致。

4 实际资料处理与结论

实际处理要比理论模型复杂的多，一是因为数据采集过程中存在误差，而是实际的地质情况本身就非常复杂。现以某矿的一条剖面作为应用实例。测线为南北走向，长20公里，点距为40米，把野外数据做各项改正后得到重力异常曲线，通过反演得到质量分布图4。由图可以看出，反演得到的质量分布图与重力异常分布位置对应。

通过对二维重力反演成像在理论模型和实际资料中的应用研究，等效源法在二维密度反演成像中的效果在实际资料中得到了证实，在二维密度反演中，等效源反演要比一般方法简便，计算速度快，并能有效提高解释的精度。

［1］陈佩良，江玉乐.重力学教程［M］.地质出版社，2005.

［2］江玉乐，雷宛.地球物理数据处理教程［M］.地质出版，2006.

［3］冯敬英，周煕襄.等效源模型反演方法的效果［J］.成都地质学院学报，1987（2）.

［4］David A. Emilia.Equivalent Source Used as An Analytic Base for Processing Total Magnetic Field Profiles［J］.Geophysics.1973.（38）：339-348

［5］曾华霖，闞筱玲，谢婷婷，等重磁勘探反演问题［M］.石油工业出版社，1991.

［6］钟本善，周熙襄，沙椿，等效源法在重磁异常解释中应用的进一步探讨［J］.物探与化探，1986（3）：201-204.

［7］艾瑛，等效源重力反演成像的研究与应用［D］.成都：成都理工大学，2013.

［8］罗孝宽，郭邵雍.应用地球物理教程-重力［M］.北京：地质出版社，1991.