区域产值单耗的行业因素影响分析方法研究
杨斌 尚永涛 贺岩 娄建旻
摘 要:基于区域性的总体产值单耗和分行业的产值单耗数据,运用逐步回归模型建立行业数据与区域总体数据的关系,不断筛选进入模型方程的行业,最终选择出对区域总体产值单耗产生显著影响的行业,并与区域总体数据建立线性回归方程.分析了行业对区域总体产值单耗产生的重要影响,并量化出影响系数.研究结果有利于指导节能监管部门加强主要行业的节能监管力度,降低区域产值单耗,促使区域工业经济向低能耗方向发展.
关键词:区域; 产值单耗; 行业因素; 逐步回归
中图分类号: F 062.1 文献标志码: A
工业是我国主要的能源消费领域,加强工业节能是实现经济持续、快速发展的必然选择,同时有助于促使企业提高生产技术水平和企业竞争力,是企业保持可持续发展的重要途径.节能监管部门通过有效的科学管理,针对监管区域内的行业结构和能耗水平,制定符合实际的节能监管方法,能够提高区域节能管理水平,有效降低区域内的总体能耗水平[1-2].
国外工业节能信息化建设中有强大的数据挖掘应用软件作为支撑.国内工业节能信息化系统中数据分析的应用还较少,数据分析结果的成功应用还需进一步挖掘.本文的研究即为数据挖掘技术在工业节能信息化中的应用探索.
1 区域产值单耗
能源消耗可用产值单耗或产品单耗两种方式表示.产值单耗,即单位产值综合能耗,是指统计报告期内,综合能耗与期内用能单位总产值或增加值的比值(本文使用单位总产值).产品单耗,是指统计报告期内,用能单位生产某种产品或提供某种服务的综合能耗与同期该合格产品产量(工作量、服务量)的比值.对于一个区域而言,由于其包括多个行业、多个企业,并且同一企业有多种产品,因此产品单耗无法计算,但区域产值单耗可计算[3],因此选取产值单耗作为能源消耗的计量,即
G=a1b1+a2b2+…+anbn
(1)
式中:G为区域产值能耗;a1、a2、an分别为行业1、行业2、行业n产值单耗;b1、b2、bn分别为行业1、行业2、行业n产值比重;n为区域内的行业数.
因此,区域产值单耗可反映一个区域内的总体能耗水平,是评价区域能耗水平的重要指标.在保证区域产业结构合理发展的同时,降低区域产值单耗是节能监管工作的实际体现.区域单位为省级或市级时,需考虑的重点用能单位的行业数量很多,同时由于行业之间相互影响,行业的产值单耗存在相关关系,因此难以发现哪些行业的产值单耗对总体产值单耗有显著影响.本文运用数学模型分析行业产值单耗与区域总体产值单耗的关系,找出对区域产值能耗有显著影响的行业并进行重点关注和监管,逐步优化产业结构.在保证经济结构合理条件下提高对区域产值单耗影响大且低于区域总体产值单耗的行业产值比重,降低区域产值单耗,促使区域工业经济向低能耗方向发展.
2 逐步回归的行业因素分析模型
2.1 模型简介
逐步回归模型是根据多元回归分析法、求解求逆紧凑变换法及双检验法(即引进和剔除检验法)建立的能够反映各个要素之间变化关系的最优回归模型.该模型仅包含对因变量有显著影响的自变量.它实质上是在多元线性回归分析的基础上派生出的一种研究和建立最优多元线性回归方程的算法.
为了得到区域内哪些重点行业对区域总体产值单耗有显著影响,本文基于产值单耗月度数据建立逐步回归行业因素分析模型.当模型中行业较多时,有的行业可能对总体产值单耗影响不大,而且各行业之间可能不完全独立,存在关联.在这种情况下可使用逐步回归分析的方法,对行业的产值单耗进行筛选,最终得到与总体产值能耗关系较密切的重点行业,并建立这些重点行业产值单耗与总体产值单耗的回归分析方程[4-6].
2.2 模型步骤
建立逐步回归行业因素分析模型的步骤为:
(1) 根据各行业的产值单耗数据,求得初始相关系数矩阵,确定变量存在相关关系.
(2) 运用求解求逆紧凑变换法对相关系数矩阵进行变换,并找出偏回归平方和最大的变量并将其引入回归方程.
(3) 剔除变量检验.找到引入的所有变量的偏回归平方和最小的变量进行剔除检验(F值即F统计量值检验),确定变量是否要剔除.
(4) 重新计算相关系数矩阵,转入第(2)步,直到再无显著变量可引进时终止,并求出最优回归模型.
根据回归过程,最终得到部分行业组成的区域总体产值单耗的回归模型为
G=a1d1+a2d2+…+andn+C(2)
式中:d1、d2、dn分别代表行业1、行业2、行业n系数;C为常数项.
少数行业的产值单耗可解释区域总体产值单耗.加强有效监管手段,促使这些行业的产值单耗降低,则可有效降低区域总体产值单耗.并且从长期产业结构调整的角度来看,在保证经济结构合理的条件下,要重点提高这些行业中产值单耗低于区域总体产值单耗的产值比重,抑制高于区域总体产值单耗的行业产值比重增长.
3 案例分析
3.1 区域产值能耗模型建立
本文选取某市22个重点用能单位行业2011年1月—2013年11月共35个月的产值单耗月度数据作为样本,即为实际值.对数据作均值处理以保证数据的有效性,记为实际数据的相对值.由于回归过程为线性分析,运用相对值与实际值的计算效果相同,因此应用相对值计算,建立逐步回归的行业因素分析模型,并进行模型验证.
经过数据处理后发现,2011年1月的数据为离群数据,因此剔除该月度数据,即取2011年2月—2013年11月共34个样本进行计算.
3.2 模型结果验证
由于解释变量之间存在多重共线性,故采用判定系数检验法检验多重共线性.模型中每一个被解释变量分别以其余解释变量为解释变量进行回归计算,并计算相应的拟合度,也称判定系数.如果判定系数较大,则说明该被解释变量可用其它解释变量的线性组合代替,即解释变量之间存在共线性.
运用样本数据计算22个行业之间的多重共线性关系,得到各行业的拟合度如表1所示.
从表1中可看出,多个变量的拟合度均在0.9以上,说明解释变量之间存在较强的共线性.因此,通过逐步回归分析模型,消除解释变量之间的共线性,最后选取了部分行业的产值单耗作为解释变量,区域产值单耗为被解释变量,建立回归方程,即
y=0.859x4+0.118x5+0.062x13+0.393x15+
0.042x17+1.831x21+4.931x22-180.4(3)
式中:y为区域总产值单耗;x4为烟草制品业产值单耗;x5为纺织服装、鞋、帽制造业产值单耗;x13为电力、热力的生产和供应业产值单耗;x15为饮料制造业产值单耗;x17为化学原料及化学制品制造业产值单耗;x21为交通运输设备制造业产值单耗;x22为电气机械及器材制造业产值单耗.
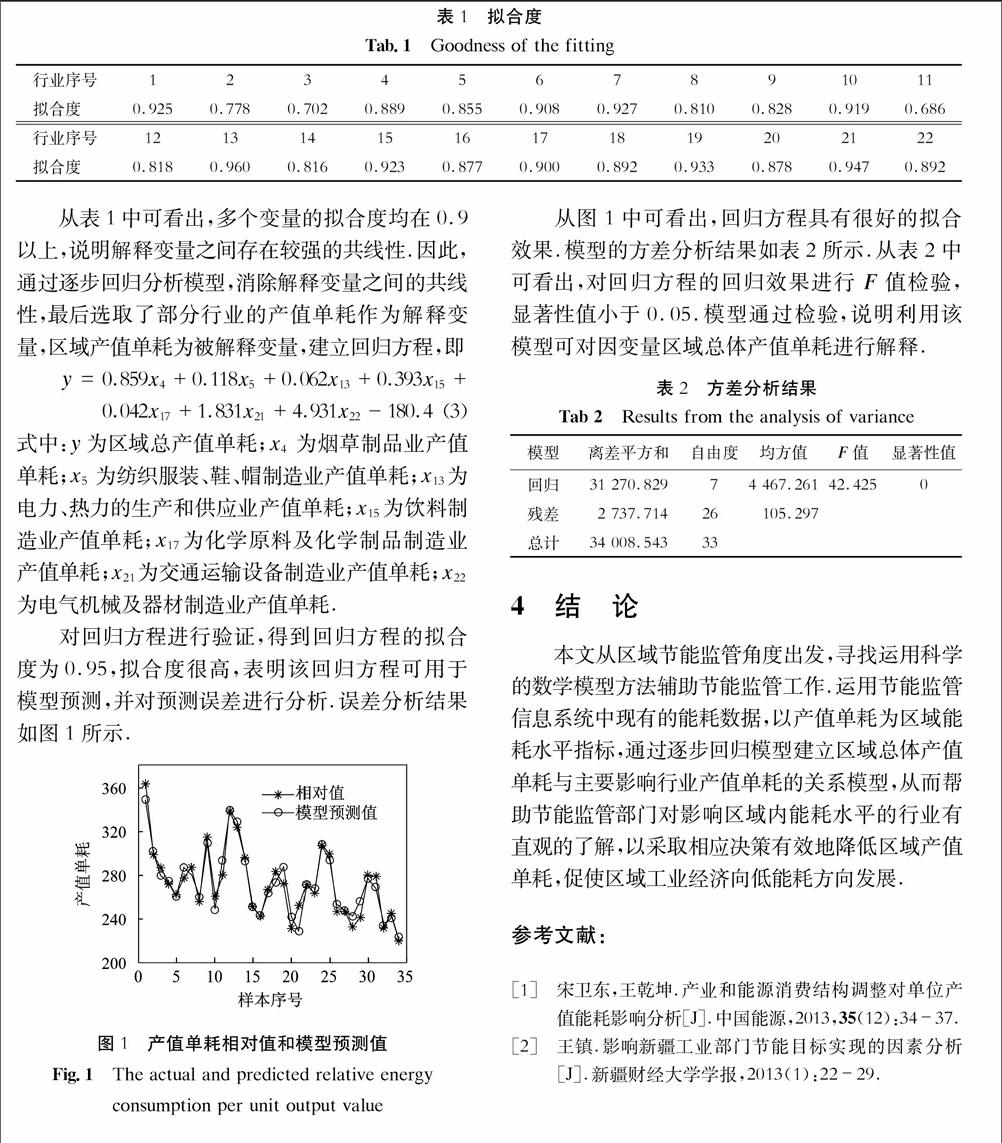
对回归方程进行验证,得到回归方程的拟合度为0.95,拟合度很高,表明该回归方程可用于模型预测,并对预测误差进行分析.误差分析结果如图1所示.
从图1中可看出,回归方程具有很好的拟合效果.模型的方差分析结果如表2所示.从表2中可看出,对回归方程的回归效果进行F值检验,显著性值小于0.05.模型通过检验,说明利用该模型可对因变量区域总体产值单耗进行解释.
4 结 论
本文从区域节能监管角度出发,寻找运用科学的数学模型方法辅助节能监管工作.运用节能监管信息系统中现有的能耗数据,以产值单耗为区域能耗水平指标,通过逐步回归模型建立区域总体产值单耗与主要影响行业产值单耗的关系模型,从而帮助节能监管部门对影响区域内能耗水平的行业有直观的了解,以采取相应决策有效地降低区域产值单耗,促使区域工业经济向低能耗方向发展.
参考文献:
[1] 宋卫东,王乾坤.产业和能源消费结构调整对单位产值能耗影响分析[J].中国能源,2013,35(12):34-37.
[2] 王镇.影响新疆工业部门节能目标实现的因素分析[J].新疆财经大学学报,2013(1):22-29.
[3] 全国能源基础与管理标准化技术委员会.综合能耗计算通则GBT 2589—2008[M].北京:中国标准出版社,2008.
[4] 马庆国.应用统计学:数理统计方法、数据获取与SPSS应用[M].北京:科学出版社,2008.
[5] 杨有,李晓虹.多重共线性的逐步回归检验分析[J].重庆三峡学院学报,2006,22(3):39-41.
[6] 李松臣,张世英.基于逐步回归法的人口出生率影响因素分析[J].统计与决策,2008(4):7-9.

