含逆变器电源的电力系统短路电流计算

杜公言 曹 炜

（上海电力学院，上海 200090）

由于逆变器的构造和工作原理与传统同步发电动机截然不同，当电网运行中发生短路时，通过逆变器并网的电源提供的短路电流其特性也将不同于传统的发电机。当发生短路时，对于容量小的逆变器电源，逆变器的保护将立即动作切除逆变器以保护其自身不被损坏[1]；但容量比较大的逆变器电源通常要求具有低电压穿越功能，即短路后仍然并网运行，以给电网提供电压支撑，提高系统运行的稳定性[2]。因此，具有低电压穿越功能的逆变器短路过程中的动态特性，不但会影响电力系统短路电流的特性和大小，还可能会影响到短路电流计算的方法。使传统的电力系统短路电流计算方法不能适用于含逆变器电源的系统短路电流计算。

本文首先比较了传统旋转电机电源与逆变器电源短路后的暂态过程的不同，指出传统的短路电流计算方法不适于含逆变器电源电网的短路电流计算。然后提出了含逆变器电源电网的短路电流计算方法，编程实现后用来计算某配网的短路电流。

1 逆变器电源短路电流特性

逆变器电源并网在正常运行时，一般工作在恒功率（或 MPPT）状态。当系统发生短路时，逆变器端电压大幅下降，此时由于恒功率控制目标，逆变器控制电路会调大控制电流值，使逆变器提供的短路电流急速大幅增加，电流增加导致发热，有可能损坏电子阀门。短路电流瞬时值大于2倍额定电流的持续时间小于 200μs，根据实验和仿真都表明逆变器控制电路将短路电流限制在标准规定的限值范围内所需的时间最多只有10ms[3-4]。

本文用 Matlab/Simulink软件仿真逆变器电源（示意图见图 1）分别在正常运行、过载、空载情况下发生短路，对应的电流波形如图2所示。

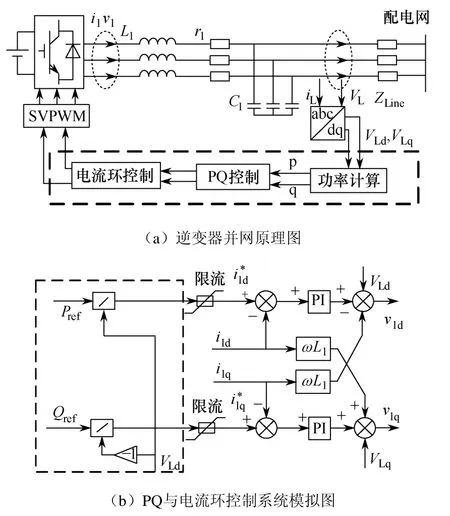
图1 并网逆变器电源及其控制系统

图 1中：i1、v1是逆变器轴输出电流、电压；Pref、Qref是有功、无功指令；VL是线路测量电压。

由图2知，无论是在正常运行情况下，还是在过载、空载情况下发生短路，短路电流均在 10ms内被限制在190A，约为额定电流的1.36倍，为图1（b）中电流限值，与前述文献[3-5]中描述的情况一致。

从图2和前述各文献中的逆变器短路电流波形中还可看到，逆变器主要提供短路电流周期分量，几乎没有暂态直流分量出现在0～10ms以内的限流动态中。

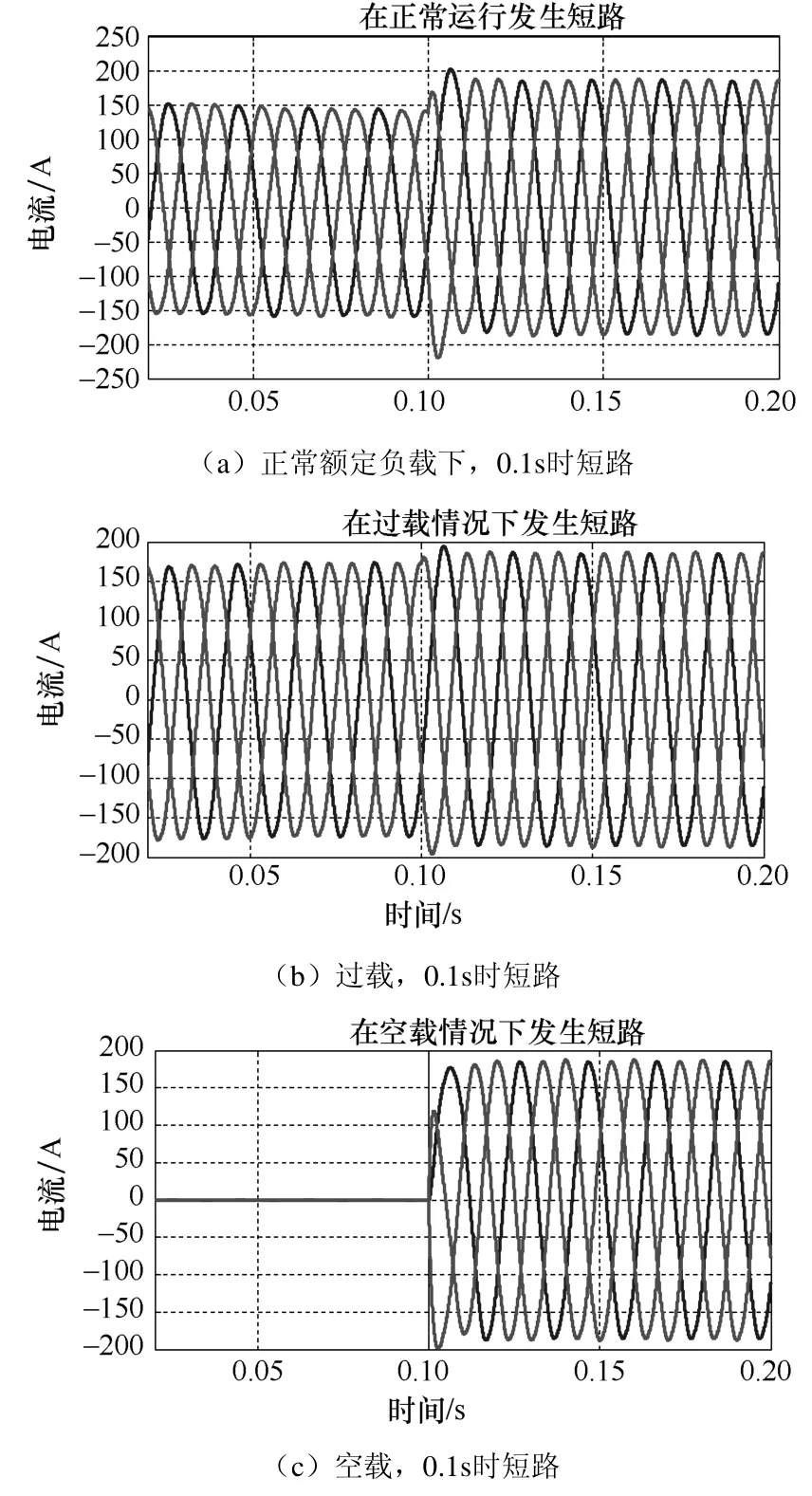
图2 逆变器电源短路电流波形

由于逆变器快速限流作用，当短路距逆变器较近足以起动限流作用时，在工程计算短路电流时可忽略逆变器限流动态，近似认为逆变器电源是内阻抗无穷大的纯交流电流源，可用相量表示，其电流有效值为限流有效值，相位由短路后的控制方式决定。例如，文献[2]提出一个低电压穿越时的有功无功控制方案，采用该方案，当电网电压跌落时，电流幅值控制策略将电流限制在该文规定的值，并调整给定相角refθ来调整逆变器的无功输出，其有功输出根据要求的无功输出和限流值决定。这意味着故障发生以后逆变器输出电流相位由低压穿越过程中要求输出的无功功率决定。

假设短路之前，输出电流的相位为0φ，短路之后输出电流相位改变为1φ。则短路后，逆变器等效电流源注入电网电流的相位较短路前改变了γ=φ1-φ0。而同步发电机等效电压源的电势相位是不变的。

从对图3电路的仿真结果也可观察到这种逆变器提供的短路电流相位的变化（图3）。为了便于观察，图3也提供了 50Hz标准波形图以便与短路电流仿真波形进行相位比较。由图3可测得该例短路后电流相位较短路前落后12°左右。

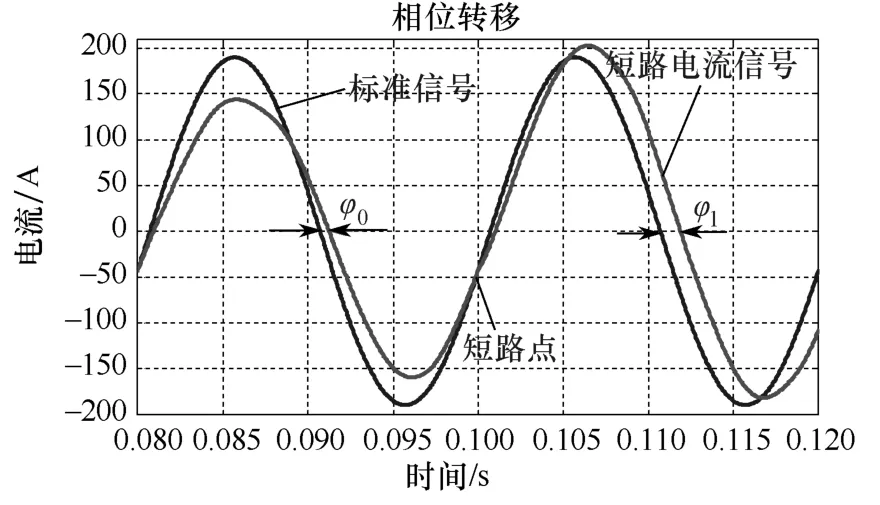
图3 短路电流相位变化

2 含有逆变器电源的电网短路电流计算方法

在传统的电力系统短路计算方法[6-8]中，认为短路电流是正常分量和故障分量的叠加，用故障端口的开路电压除以短路回路的阻抗求得。当短路前后电网中所有电源的状态不发生突变时，故障端口的开路电压即等于短路前该端口的正常工作电压。因此，可直接求得短路点的短路电流

f点短路时任一节点的电压

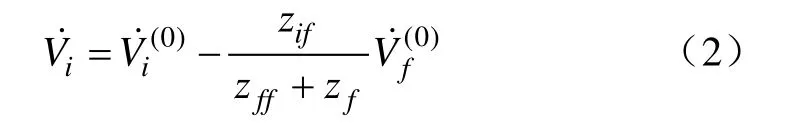
在式（1）、式（2）中，Zf为故障点f的故障阻抗；Zff为故障点f的自阻抗，也称输入阻抗，是节点阻抗矩阵第f行第f列的元素；Zif为故障点f与节点i之间的互阻抗，是节点阻抗矩阵第i行第f列的元素。

任一支路i-j的电流

式中，k为变压器的变比（图4），对无变压器支路k取1。

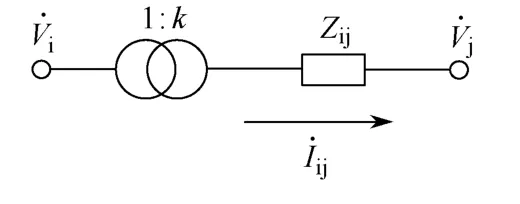
图4 含变压器支路

电网含逆变器电源时，电网中的传统电源仍可看作电势不变的电压源；而逆变器一般在 10ms内即可成功地将电流稳定地限制在限值[4-5]，忽略逆变器电源快速的限流动态，在其限流起作用后可将其看作电流源，该电流源的电流值不等于且一般大于短路前的正常工作电流；即，如果忽略逆变器极其短暂的限流起动动态，短路前后作为交流电流源的逆变器稳态电流是突变的，由短路前的负荷电流突变为短路后的电流限值，例如1.5倍的额定电流

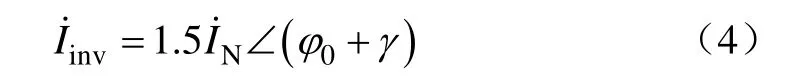
式中，IN为逆变器的额定电流；φ0为短路前逆变器输出电流相位；γ短路后逆变器输出电流相位变化。由于上述原因，含逆变器电源的电网短路后，故障端口的开路电压不再等于短路前的正常工作电压。因为故障端口的开路电压等于短路前该端口的正常工作电压成立的前提是短路前后电源状态不变，即电压源的电势等于短路前瞬间的电势（例如同步发电机=）；如果有电流源，电流源的电流也等于短路前瞬间的电流。

由此，传统短路电流计算方法不适于计算含逆变器电源的电网的短路电流。

考虑电网中的逆变器电源时，其短路电流仍可用节点电压方程

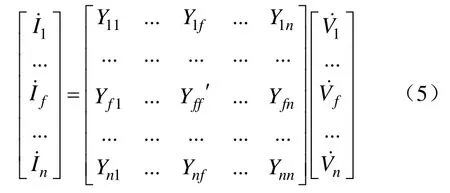
式中的n个节点包含电源节点、负荷节点、和短路节点。

当电源是传统的同步发电机时，由式（6）计算该电源所连节点注入电流。

当电源是逆变器时，由式（4）计算该电源所连节点注入电流；负荷节点、短路节点的注入电流为零。

注意传统方法中，短路节点的注入电流不为零，为If。对应地，传统方法中的节点导纳或节点阻抗矩阵中，不考虑故障阻抗Zf，而在采用式（5）的考虑逆变器的新方法中，节点导纳矩阵或节点阻抗矩阵中要考虑故障阻抗Zf，具体方法是用式（7）修正传统方法中的节点导纳矩阵对应元素。

式中，Yff为传统方法导纳矩阵中第f行f列元素；Zij为传统方法阻抗矩阵中第i行j列元素。

若是三相金属性故障即Zf=0，式（5）中对应的第f行或列的导纳将为无穷大，此时Vf=0，再联系式（7）中电流向量的第f个元素也为0，可删除公式（5）中的第f行和第f列，并不影响其求解。

由式（5）求解出各节点电压，再由式（3）计算与短路点f相连的各支路短路电流求代数和即为短路点的短路电流。

3 编程实现与算例分析

将上述过程按图5流程编程实现，用来计算图6所示系统的短路电流。

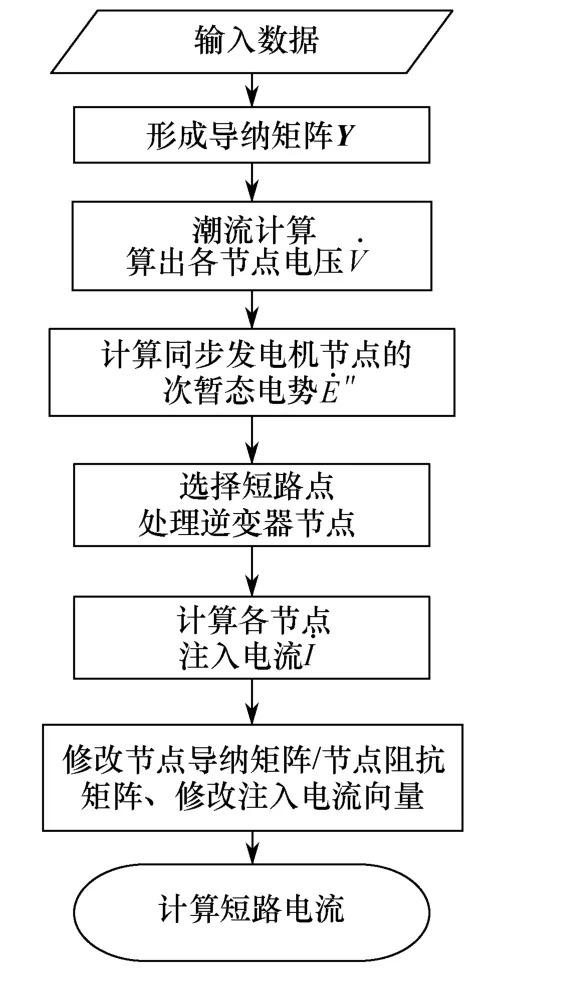
图5 短路电流计算流程

3.1 算例描述

图6是33节点配电网，不计网损时总负荷为3715+j2300kVA。

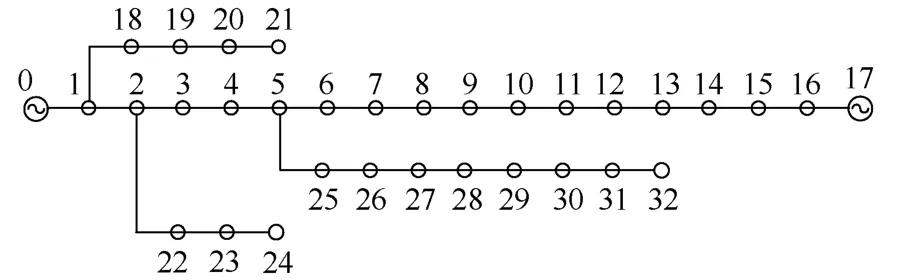
图6 33节点网络

零号节点为电力系统等值节点，在潮流计算中设为平衡节点，设该点短路时系统侧短路电流为10kA，取基准功率为1MVA、基准电压为12.66kV，则该点系统等值电抗标幺值为= 0.0046；17号节点设为分布式电源节点，可为旋转电机（同步发电机或异步发电机）也可为逆变器电源。同步发电机的次暂态阻抗为=0.10，额定功率为3200+j640kVA，折算到统一基值下的标幺值为0.03；17号节点的分布式电源通过变比1∶1.01的变压器联网。其他各节点功率、各支路参数见文献[9]。

假设17号节点无论接何种类型的分布式电源，短路前电网都运行在相同的潮流下，分布式电源提供的功率为1600+j320kVA。分别采用下述五种方式计算短路电流。

方式一：电网中没有分布式电源；

方式二：电网中的分布式电源都是同步（或异步）发电机，负载率为0.5；

方式三：电网中的分布式电源都通过逆变器接入，但短路电流计算采用传统方法。

方式四：电网中的分布式电源都通过逆变器接入，负载率为 0.5，即假定其额定功率为3200+j640kVA，采用改进方法计算短路电流。

方式五：电网中的分布式电源都通过逆变器接入，负载率为 1.0，即假定其额定功率为1600+j320kVA，采用改进方法计算短路电流。

3.2 算例结果分析

将各种计算方式下不同点短路时的短路电流列于表1，联系图6可得下列规律：

1）对比计算方式一与计算方式二、四、五的短路电流计算结果可知，考虑分布式电源后，各点短路的电流都较无分布式电源时有所增加，且短路点距分布式电源越近，短路电流增加越多。

2）对比计算方式二与计算方式四、五的计算结果可知，逆变器接入的分布式电源导致的短路电流的增加远小于旋转电机式的分布式电源（同步或异步发电机）导致的短路电流增加，且短路点距分布式电源越近，这种趋势越明显。

3）对比计算方式三与计算方式四、五的结果可知，含有逆变器接入的分布式电源的电网，用传统的短路电流计算方法所得结果小于本文提出的方法所得结果。且短路点距分布式电源越近、分布式电源负载率越低，这种趋势越明显。

将各种计算方式下不同点短路时的分布式电源端电压（即第17节点的电压）列于表2，联系图6，可做下列推论：

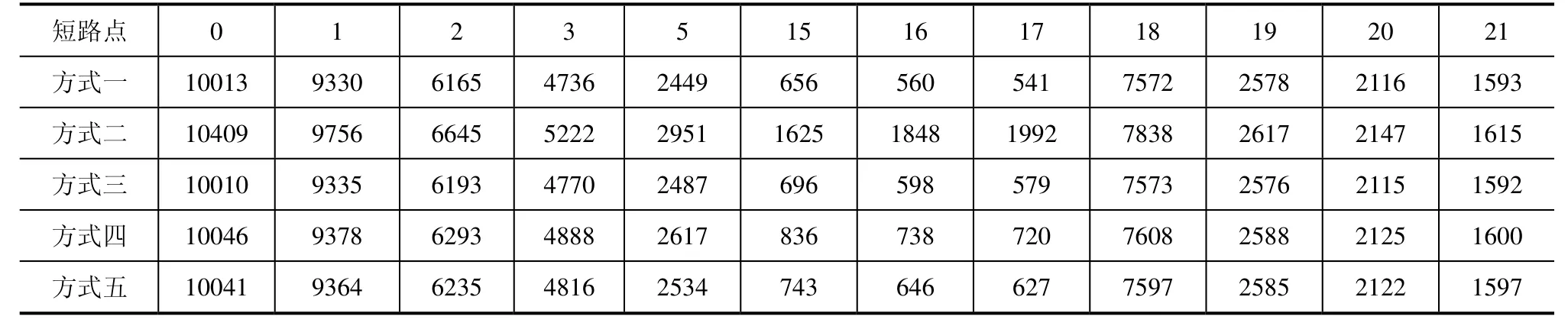
表1 短路电流值/A

表2 各节点短路时，第17号节点的电压/pu

（1）短路后，分布式电源对配网电压都有一定的支撑作用，但同步发电机式的分布式电源电压支撑作用更明显。

（2）对含逆变器电源的分布式电网，当短路点距分布式电源较近时，本文提出的算法是合理的；但该算法不适用于当短路点距分布式电源较远时。如表2中，第21节点短路时，计算方式三下第17节点的电压约为1.01pu.，而潮流计算所得该点短路前的电压也为1.01pu.。计算方式三（即采用传统方法计算短路电流），假定短路前后逆变器电源的电流不变，而在方式三下该电源的电压也几乎等于短路前的电压，说明此时17节点的逆变器电源其控制电路中的限流环节不会起动，仍能工作在原来的定PQ（或 MPPT）方式。如用本文提出的方法计算（即方式四，认为该电源提供的电流是额定电流的 1.36倍），实际高估了该电源的输出功率，该节点电压也将高达1.28pu.，不符合实际情况。但从表1中看到，仅就短路点短路电流而言，此时对短路点电流高估的相对量并不大，只有（1600-1592）/1592=0.5%。

4 结论

本文分析了传统电源与逆变器电源短路特性的不同，指出逆变器电源交流测短路后短路电流中不含暂态直流分量，同时可忽略逆变器电源短路后快速的限流动态，将逆变器电源看作短路前后稳态电流发生突变的恒流源来计算短路电流周期分量。并提出一种能够适用于既含传统旋转电动机电源又含逆变器电源电网的短路电流计算算法。结果表明，该改进方法适用于当短路点距逆变器电源较近时，当短路点距逆变器电源较远时，短路电流会变大，但误差百分比仍在可接受的范围内。

[1] 刘扩军. 电压型逆变器的短路保护[J]. 机车电传动,1992(5): 31-35.

[2] 党克, 胡金, 严干贵. 光伏逆变器低电压穿越控制策略的研究[J]. 电力电子技术, 2013, 47(11): 22-24.

[3] 杨文华. 并网光伏电站短路特性分析与计算[J]. 宁夏电力, 2011(6): 5-7, 21.

[4] 柳彬, 谢炜, 余跃听, 等. 逆变电源短路保护及限流策略[J]. 舰船科学技术, 2011, 33(8): 95-98, 129.

[5] 刘健, 林涛, 同向前, 等. 分布式光伏电源对配电网短路电流影响的仿真分析[J]. 电网技术, 2013, 37(8):2080-2085.

[6] 单龙飞. 含分布式电源的配电网短路计算[D]. 郑州:郑州大学, 2013.

[7] 何仰赞, 温增银. 电力系统分析[M]. 武汉: 华中科技大学出版社, 2011: 133-160.

[8] 西交. 清华, 浙大等联合编写.电力系统计算[M]. 北京: 水利电力出版社, 1978.

[9] Mew E. Baran Felix F. Wu. Network reconfeiguration in distribution systems for loss reduction and load balancing. IEEE Transactions on Power Delivery, 1989,4(2): 1401-1407.