高空核电磁脉冲晚期效应对电网稳定性影响的研究

赵志斌 柯俊吉 马丽斌

（华北电力大学新能源电力系统国家重点实验室，北京 102206）

高空核爆电磁脉冲（HEMP）的晚期效应即E3效应（简称HEMP E3效应），这种由高空核爆炸引起的低频（约0.017Hz以下）、低幅值（约为数十伏/km）的电磁脉冲[1]会在交流输电系统中产生低频的准直流，从而导致系统中变压器发生直流偏磁现象、中性点过流保护跳闸、继电器误动等后果，最终影响电力系统的正常运行。

20世纪 80年代开始了对于这一问题的研究，目前理论分析较少，研究主要依靠实验的方式展开。国外学者作了大量研究工作，提出了不少的分析和计算方法，也做了相关验证性的实验。如 Rackliffe提出根据通过计算太阳风暴的地磁感应电流的方法，计算MHD-EMP的感应电流，最后对准直流电源系统中的感应电流进行了计算[2]；之后Meliopoulos用实际算例对 Rackliffe的阐述进行证明，并在473英里长线路系统上进行了两者的比较与分析[3]。在模型计算方面，Lehtinen等将直流偏磁电源串联到传输线网络模型中[4-5]，然而 Albertson等人则将直流偏磁电源串联接到变压器中性线的接地点之上[6]。总而言之，各个计算方法不同之处在于直流激励的引入方式不同。

国内学者对HEMP晚期效应的研究：Jin Liu等人采用了传输线模型[7-8]计算了核电磁脉冲对电力系统的效应和HEMP作用下传输线的感应电流计算[9-10]。然而，目前国内文献都未曾考虑HEMP晚期效应对电力系统稳定性的影响。

基于国内外学者的研究成果，本文主要作如下研究：首先建立了地磁感应电流的电网模型，将地磁感应电流的计算问题转化成电路问题，并采用Lehtinen与Pirjola的方法求解；然后以某750kV电网为实际案例计算地磁感应电流水平从而验证模型与算法在此计算条件下的可行性；最后从断路器、自耦变压器等方面分别考虑高空核电磁脉冲晚期效应对电力系统的影响。

1 高空核电磁脉冲晚期效应产生地磁电流模型

1.1 计算模型

由于计算 HEMP E3效应感应电流的过程即为HEMP E3效应感应电场通过接地点作用于电网产生电流，所以可以将电场的作用等效为网络中的电压源，将HEMP E3效应感应电流的计算转化为电路问题，从而通过等效的电网模型计算电网的 HEMP E3效应感应电流水平。

将变电站中的变压器和电抗器等元件连接并等效得到变电站的等效模型。若变电站内有两台及以上变压器并列运行，等效时应把相应元件的电阻并联。变电站的接地电阻也包括感应电流等效模型，用Rd表示，其流过的感应电流为三相的总和，单相模型中的等效接地电阻应为实际三相的 3倍。即3Rd。

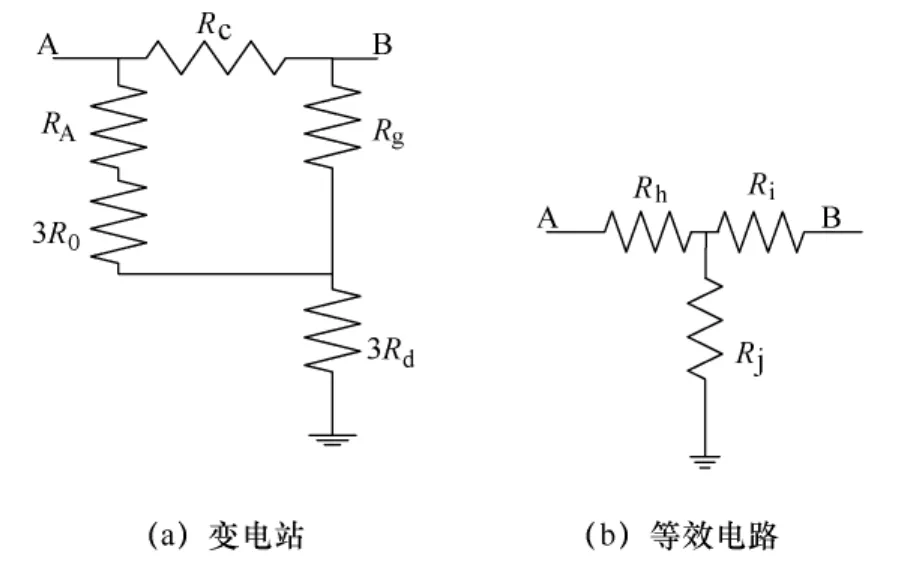
图1 变电站等效电路图

1.2 高空核电磁脉冲晚期效应的特性

高空核电磁脉冲晚期效应简称HEMP E3，文献[5]指出若核爆炸的海拔高度介于 130～500km 之间，那么HEMP E3的影响区域达最大值。HEMP E3的时域波形采用了IEC 1000-7中给出的双指数函数波形。其中HEMP E3出现于1～1000s之间，感应电场为水平方向。HEMP E3电场波形如图所示，其峰值为 38V/km，上升时间约 0.9s，正脉冲半宽度20s，负脉冲半宽度130s。

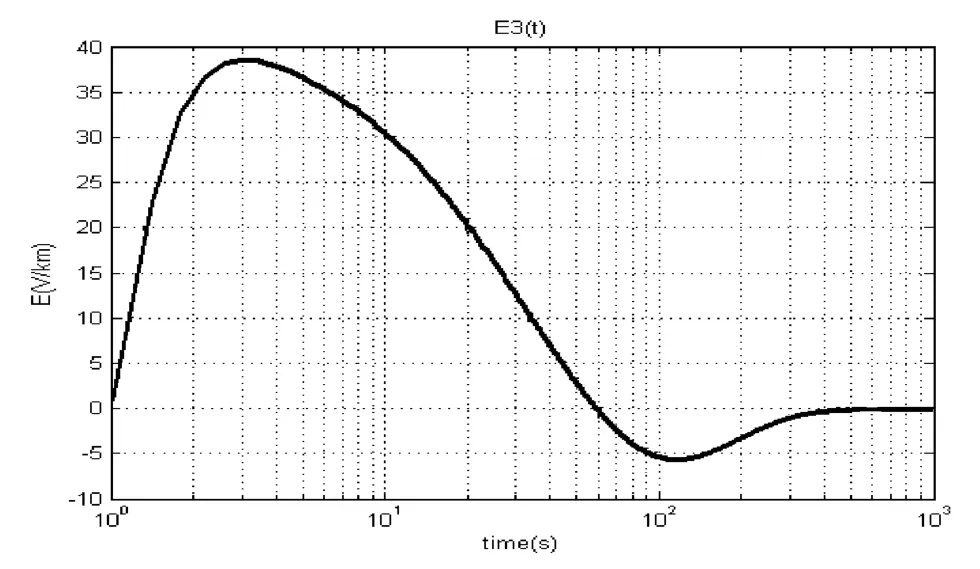
图2 HEMP E3的标准波形图

1.3 计算方法

在电网模型中地面感应电场的作用等效为施加于接地点两点间的电压源，其值是电场的沿线积分，即

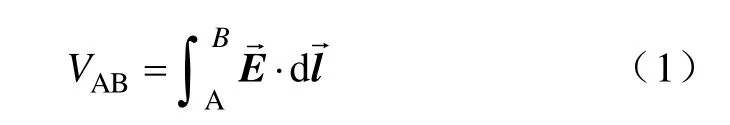
计算时，把整条线路→分成N段，线路的某一小段[i,j]内近似成直线，看成是均匀的，所以此段线路对应的等效电压源如下式所示：

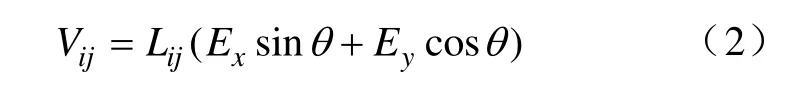
式中，Lij是线段长度，Ex、Ey分别是本段内与地面电场平行和垂直的北、东向分量，θ 为线段和y轴（东）之间的夹角，因此对应整条线路的等效电压源即为各线段电压之和。

经上述方法等效之后，则可以得到一只包含电阻和电压源的电路网络，其中网络的节点即为变电站，每个节点和地间的电阻则是变电站接地支路的等效电阻，不同的节点和节点间的电阻是不同变电站之间输电线路的等效电阻，节点与节点之间的电压源是 HEMP E3电场在不同变电站接地点间的等效电压源。

图3 电网任意两节点等效模型图

当电网节点较多时，若使用回路电流法或节点电压法，以形成电路的矩阵方程，此方法比较繁琐，运算速度较为缓慢，为了提高计算的运行速度且便于编程，应用Lehtinen与Pirjola的方法求解。对于一个N节点的电网模型，其中任意两点i和j间的等效电阻是Rij，接地支路的等效电阻为Z，两点间的等效电压源Vij，各条输电线路上流过的感应电流Iij可由Lehtinen与Pirjola的方法计算得到：

2 高空核电磁脉冲晚期效应对系统稳定性的影响

为了提高电力系统运行的可靠性，首要任务是应加强系统抵抗干扰能力和完善系统结构。因此十分有必要对 HEMP E3效应作用下电网的感应电流水平进行研究，并以此来判断其对电网的威胁。

2.1 HEMP E3效应作用下的感应电流水平

本文以电压等级较高、覆盖面积大的某 750kV电网为例分析了 HEMP E3效应在电网中产生的感应电流，由于没有公开资料给出E3电场的空间分布特性，所以在计算时，未考虑高空核爆炸电磁脉冲E3效应在不同空间位置的变化。

某750kV电网如图4所示。本文计算了均匀分布的HEMP E3电场下（即方向和大小d不随位置改变而变化）。

图4 某750kV电网示意图

图5给出了最大情况下流过各变电站每台变压器的感应电流。可以看出，在格尔木变电站的感应电流水平最高，可达 4000A。考虑到在变压器中性点串联小电阻，可以有效降低感应电流，图5给出了不同电阻值情况下的计算结果。从图中可以看出，即使采用 10Ω的电阻，部分变压器地磁感应电流的最大值仍超过1000A。

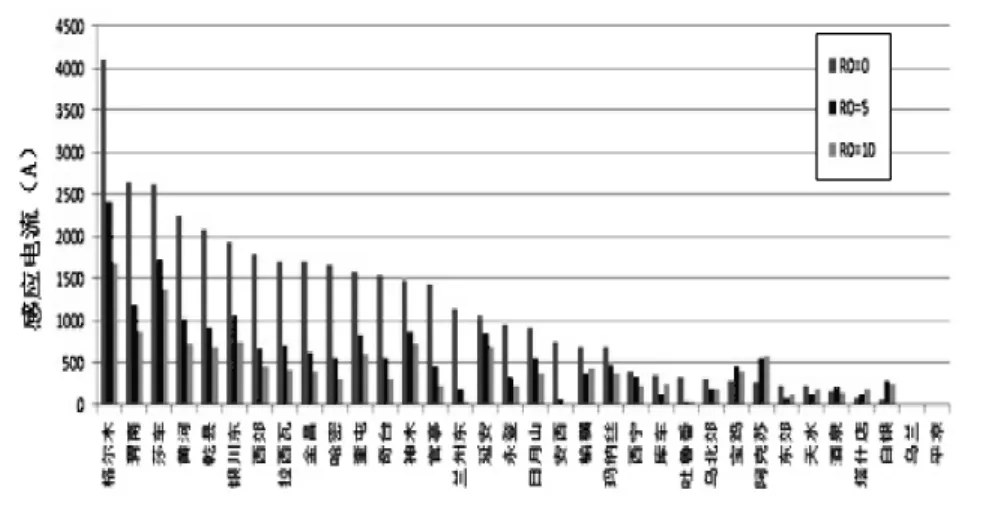
图5 750kV各变电站在HEMP E3作用下的感应电流

由电磁感应定律可知:时变的磁场在大地中感应出电场，此地电场又会在接地的导体网络中产生地磁感应电流，称此感应电流为 SS-GIC（Solar storm-geomagnetically induced current）。同理 HEMP E3效应所感应出的电流被称为 MHD-GIC（magnetohydrodynamic-geomagnetically induced current）。二者频率都极低，近似于直流。从文献[11]中监测数据上看，太阳磁暴所导致的 SS-GIC峰值一般在50A左右，所以高空核爆炸电磁脉冲晚期效应造成的瞬时影响比太阳磁暴的影响要大得多。

据文献[12]所给出的太阳磁暴地面电场计算结果其场强峰值不超过 1V/km，SS-GIC最大不超过150A。本文所计算的MHD-GIC都以HEMP E3峰值38V/km计算，最大达到4000A。二者对比结果可以验证模型与算法在此计算条件下的可行性。

2.2 高空核电磁脉冲晚期效应感应电流对系统中断路器的影响

在断路器的开发过程中很大程度上依赖于电流中断装置的设计，而电流中断装置遵循交流电流的特性，自然电流为零时才允许电流中断。开断幅值较大的直流只能依据一般的理论认识，HVDC传输线的开关则需人工方法，在所需的直流电流中断的时间内产生一个电流零点。

如前所述，HEMP E3效应会给电网带来较大的感应电流。如图6所示，750kV传输线上HEMP E3影响下的交流电流在2s左右达到高峰，然后慢慢衰减。值得注意的是，叠加的交流和直流电流峰值时是正常交流电流的两倍左右，而且会阻碍正常的交流电流过零时间（20s左右）。

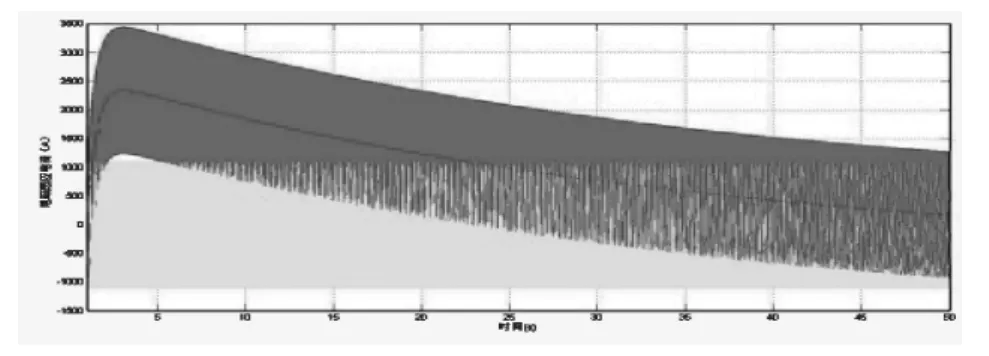
图6 某750kV传输线正常情况下的交流电流和HEMP E3效应下的交流电流

2.3 高空核电磁脉冲晚期效应感应电流对电力变压器的影响

HEMP E3效应感应电流影响下的电力变压器呈现一种非正常工作状态，变压器中流过较大偏磁电流，铁心将出现磁饱和现象，导致变压器铁心中含有直流磁通，此时铁心比正常工作时产生大考虑磁滞效应时。当存在感应电流的时候，励磁电流的波形发生了严重畸变，正半波出现尖顶，且其峰值相较于不存在感应电流时大了很多。变压器励磁电流峰值的增加，会导致变压器无功消耗增加、变压器的漏磁增加、铁心高度饱和、励磁电流畸变、变压器器身振动、油箱油温上升或金属构件局部过热、以及变压器寿命减短等不利后果。

3 结论

本文主要回顾 30余年来国内外学者对高空核电磁脉冲晚期效应的研究历程，并基于前人的研究成果分析了高空核电磁脉冲晚期效应对实际高压电网系统稳定性的影响，最终得出如下结论：

1）建立了变电站等效模型，并在此基础上应用Lehtinen与Pirjola方法计算了HEMP E3效应作用下某750kV电网HEMP E3效应感应电流，从而验证了模型与算法在此计算条件下的可行性。

2）本文对高空核电磁脉冲晚期效应对实际高压电网的可能带来的威胁进行分析，HEMP E3期间断路器存在不能正常切断故障电流可能性，HEMP E3所感应出的感应电流与工频电流叠加，导致重合闸不成功。

[1] Kenneth W, Paul R. Electromagnetic pulse and the electric network[J]. IEEE Transactions on Apparatus and Systems, 1985, 104(6): 1571-1578.

[2] Kruse V J, Rackliffe G B, Barnes P R. Load flow studies in the presence of magnetohydrodynamic electromagnetic pulse[J]. IEEE Transactions on Power Delivery, 1990, 5(2): 1158-1164.

[3] V J Kruse, D L Nickle, J J Bonk, E R Taylor.Impact of a nominal nuclear electromagnetic pulse on electric power systems[R].Martin Marietta Energy Systems,Inc, 1991：1-2．

[4] Pirjola R, Viljanen A. On geomagnetically-induced currents in the Finnish 400 kV power system by an auroral electrojet current[J]. IEEE Trans.Power Delivery, 1989, 4(2): 1239-1245.

[5] Lehtinen M, Pirjola R. Currents produced in earthed conductor networks by geomagnetically-induced electric fields[J]. Annales Geophysicae, 1989, 3(4):479-484.

[6] Boteler D H, Bui V Q, Lemay J. Directional sensitivity to geomagnetically induced currents of the Hydro-Quebec 735 kV power system[J]. IEEE Trans. Power Delivery, 1994, 9(4): 1963-1971.

[7] 谢彦召, 王赞基, 王群书. 地面附近架高线缆HEMP响应计算的 Agrawal和 Taylor模型比较[J]. 强激光与粒子束, 2005, 17(4): 575-580.

[8] 张志军. 电磁脉冲对传输线耦合规律的研究[D]. 北京: 华北电力大学, 2006.

[9] 黄聪顺, 周启明. 高空电磁脉冲作用下地面电缆屏蔽层感应电流的数值模拟[J]. 强激光与粒子束,2003, 15(9): 905-908.

[10] 敬文涛. 导弹线缆高空核爆电磁脉冲耦合效应的研究[A]. 国防科学技术大学研究生院论文, 2004.

[11] 中华人民共和国发展与改革委员会, DL/T 5224—2005. 高压直流输电大地返回运行系统设计技术规定[S]. 2005.

[12] 刘春明. 中低纬电网地磁感应电流及其评估方法研究[D]. 北京: 华北电力大学, 2009.