抗角晃动与线运动耦合干扰的捷联惯导自对准算法*

杨 波，王跃钢，杨家胜，郭志斌

（第二炮兵工程大学自动控制系，西安 710025）

抗角晃动与线运动耦合干扰的捷联惯导自对准算法*

杨 波*，王跃钢，杨家胜，郭志斌

（第二炮兵工程大学自动控制系，西安 710025）

捷联惯导系统在实际对准过程中，由于受到角晃动干扰与线运动干扰的耦合作用，难以快速高精度地完成自对准，针对该问题提出了一种抗角晃动与线运动耦合干扰的自对准算法。该算法将自对准问题转化为Wahba姿态求解问题，以消除角晃动干扰的影响；利用惯性系下的重力矢量信号的时域特性，采用时域信号处理方法来实现消除线运动干扰。仿真结果表明，该算法在角晃动干扰与线运动耦合干扰的作用下能够快速地实现自对准。

捷联惯导系统；抗干扰自对准；Wahba问题；时域信号处理；角晃动；线运动；耦合干扰

捷联惯导系统（SINS）在进入导航之前，需要先进行初始对准，对准精度直接影响导航精度［1-2］。在静止状态下，使用传统的自对准方法可以满足对准要求，然而在实际对准过程中，SINS通常处于复杂干扰环境［3-5］，如阵风干扰、海浪摇摆等，这些干扰中既有角晃动又有线运动，两种因素的耦合作用使得SINS难以完成快速高精度自对准。针对角晃动干扰的问题，文献［6］利用惯性系下重力矢量的特点，提出了间接解析式粗对准算法，并进行了摇摆台试验［7］；文献［8］提出了利用惯性坐标系下的姿态更新实时地记录载体在晃动干扰下的姿态变化的方案，该方法不需要进行粗对准。这两种算法对角晃动干扰有较好抑制效果，但对线运动干扰的抑制能力差。针对角晃动和线运动干扰耦合的情况，文献［9］提出了基于IIR滤波器的惯性系下解析对准方法，它克服了传统解析算法在舰船系泊环境下无法使用的缺点；文献［10］提出了晃动基座下SINS的抗干扰自对准算法，采用低通IIR滤波器来过滤线运动干扰信号，由于IIR滤波器为零极点系统，不同频率信号经过IIR滤波后时间延迟不同，难以通过补偿方式实现信号匹配，因此其对线运动干扰的抑制能力有限；文献［11］提出了直接提取惯性系重力矢量方向的对准算法，但需要设计FIR滤波器，由于惯导系统采样率较高，干扰信号频率较低，有用信号频率更低，因此设计FIR低通滤波器的阶次通常较高，由此导致FIR滤波的延迟时间达到数秒，需要进行延迟补偿，此外FIR滤波器稳定输出的时间长，影响了初始对准的快速性。

对于存在角晃动与线运动耦合干扰的情况，本文提出将自对准问题转化为Wahba姿态求解问题，以实现消除角晃动干扰的影响；根据惯性系下的重力矢量信号的时域特性，采用时域信号处理方法来实现消除线运动干扰的影响，从而研究获得一种抗角晃动与线运动耦合干扰的捷联惯导自对准算法。

1 基于Wahba姿态求解的抗角晃动干扰对准方法

该算法涉及到以下几个坐标系，包括导航坐标系（n系）、载体坐标系（b系）、地心坐标系（e系）、惯性坐标系（i系）等，具体含义可参见文献［8］。

对于角晃动干扰，本节将自对准问题转化为Wahba姿态求解问题以消除角晃动干扰，原理如下：

在对准开始时刻，由于i系与b系重合，所以

进而，根据四元数乘法规则对式（4）右边变形可得

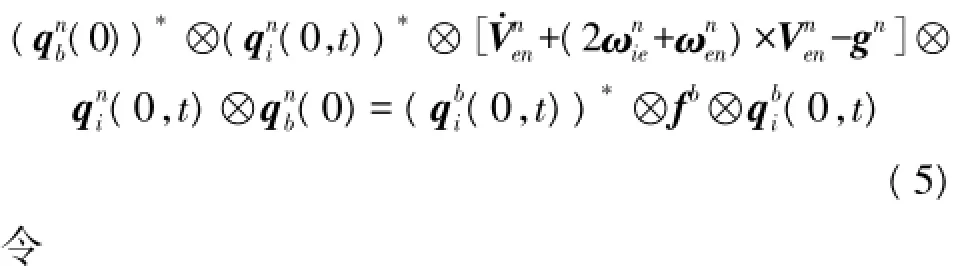
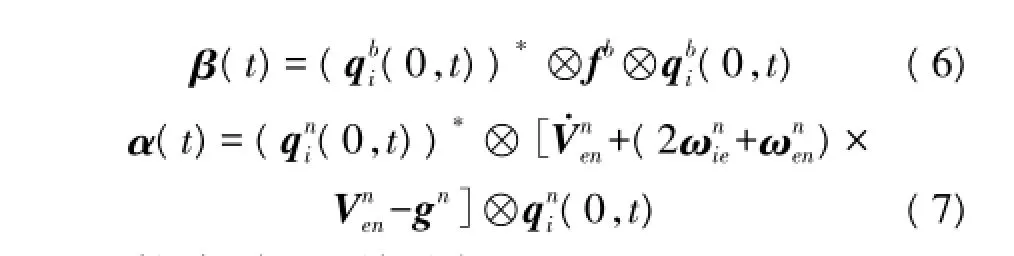
则根据式（5）关系有：

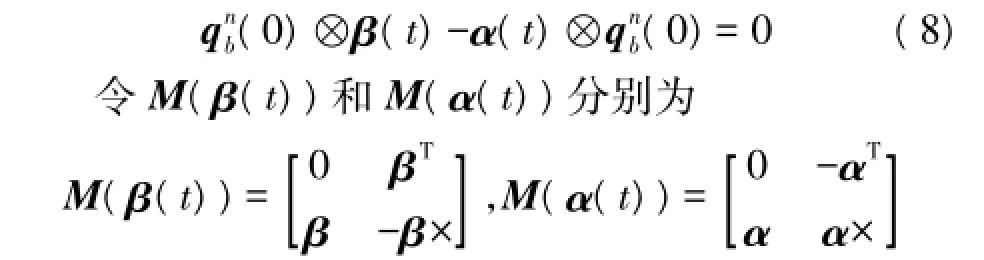
式中：β×为以向量β构成的反对称阵；α×为以向量α构成的反对称阵。则式（8）可写成

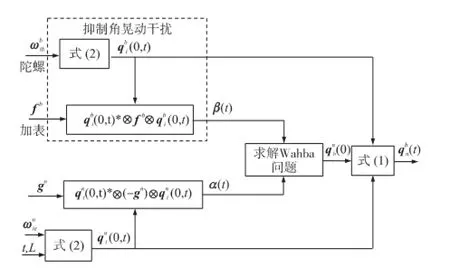
图1 抗角晃动干扰方案

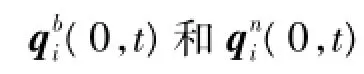
2 基于惯性系下重力矢量信号处理的抗线运动干扰对准方法

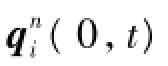
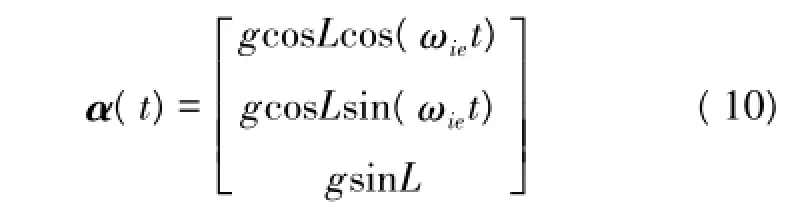
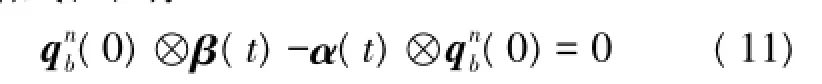
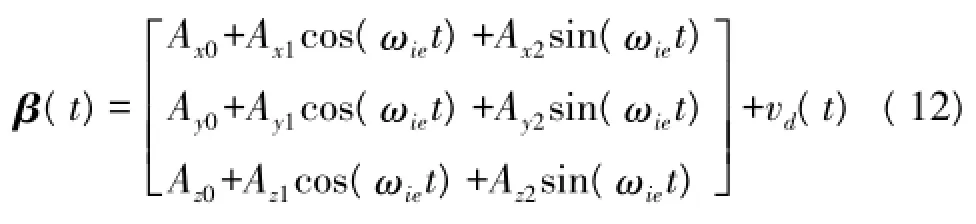
将sin（ωiet）和cos（ωiet）泰勒展开可得

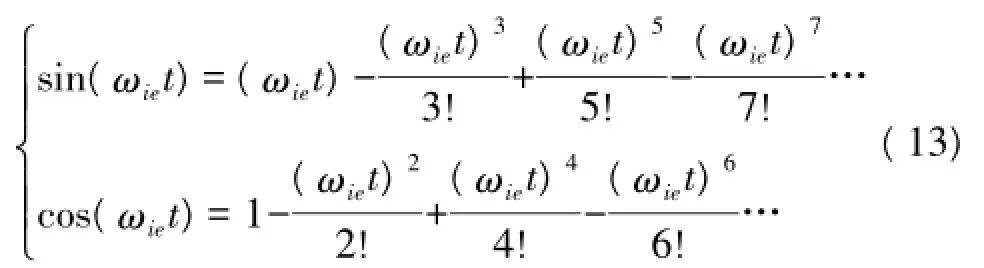
设纬度40°时，当t=280s时，α（t）为

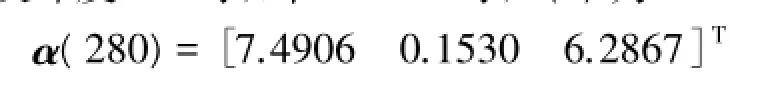
如果α（t）计算按泰勒级数展开到三阶得

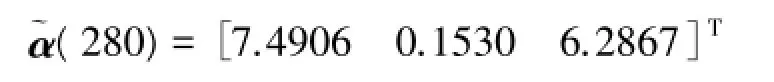
可以看出，在280 s内ωiet高阶项所占的分量很小，四阶以上可以忽略，因此α（t）可写成如下形式

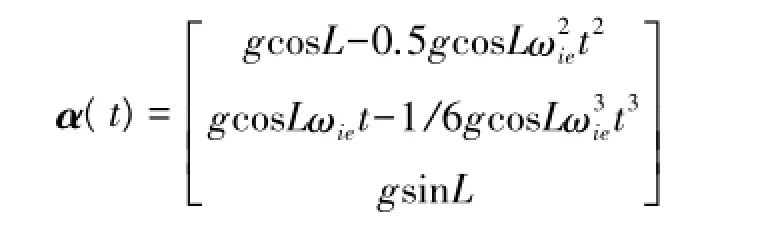
此时，对应的β（t）可表示为

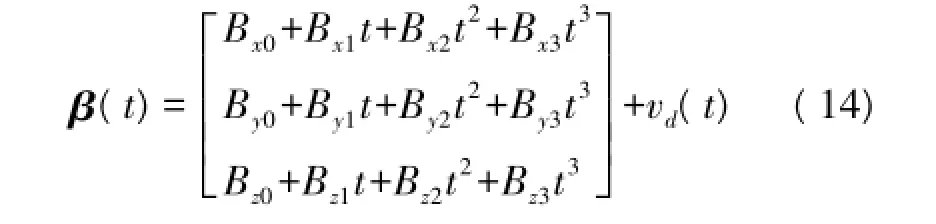
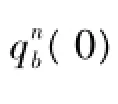
（1）可完成对准。

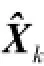
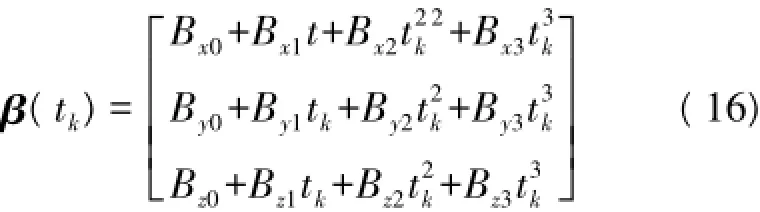
3 抗角晃动与线运动耦合干扰的自对准算法总结

由第1节和第2节的分析，可得图2所示的抗角晃动与线运动耦合干扰的自对准算法。

从图2可知，算法在抑制角晃动干扰的基础上，加入的抑制线运动干扰环节，使得算法能够处理角晃动与线运动的耦合干扰，同时，由于抗角晃动干扰措施与抗线运动干扰措施均是在时域内对数据进行处理，因此，算法不会引入时间延迟，因此不需对β（t）做时延处理。

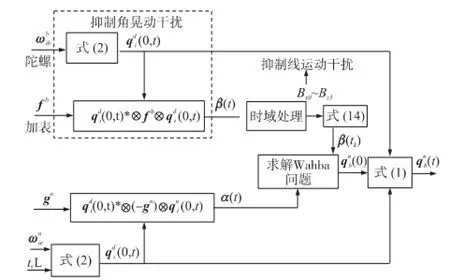
图2 抗角晃动与线运动耦合干扰的自对准算法

4 算法仿真及结果分析

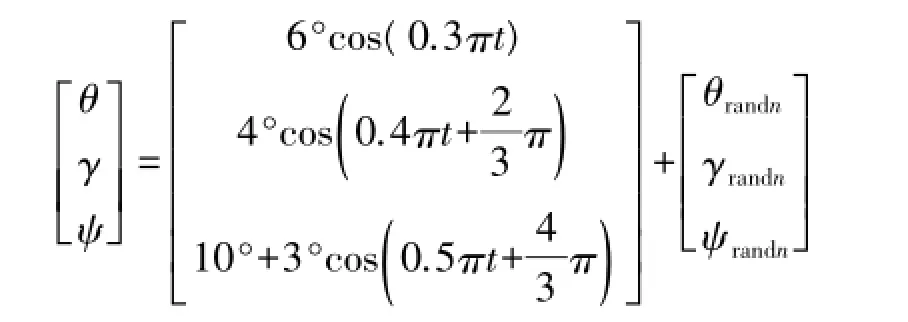
式中：θrandn为均值为0°、标准差为0.5°的白噪声；γrandn为均值为0°、标准差为1°的白噪声；ψrandn为均值为0°、标准差为0.25°的白噪声。

同时在角晃动干扰相同的情况下，设置以下两种不同的线运动干扰：

①低频线运动干扰，线运动干扰速度为：

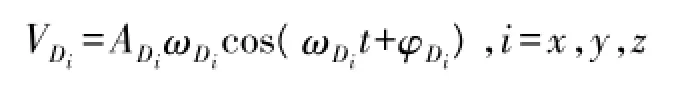
式中：ADx=0.02 m，ADy=0.03 m，ADz=0.3 m，ωDz= 2π/TDi，TDx=5 s，TDy=6 s，TDz=7 s；φDi为［0，2π］上服从均匀分布的随机相位。

②突变线运动干扰，在81 s～83 s，121 s～123 s，167 s～168 s，212 s～215 s，245 s～248 s，5个时间段内设置突变类型的线干扰，设为0.1 m/s。

在上述仿真条件设置下，分别用文献［8］算法、基于IIR低通滤波的自对准算法、基于FIR低通滤波的自对准算法和本文算法进行对准，为了表述方便，分别将这4种方法简称为原始方法、IIR低通滤波法、FIR低通滤波法、本文方法。设计的IIR和FIR低通滤波器截止频率为0.1 Hz，阻带下限截止频率为0.6 Hz，通带衰减为4 dB，阻带衰减为40 dB。二种干扰条件下的对准误差如图3～图4所示。受篇幅限制，图中只给出方位角的估计误差作为比较标准。

从图3中可以看出，角晃动与低频线运动干扰耦合情况下，原始方法的对准结果呈现剧烈地波动，且波动幅度很大，在对准快结束时方位角的估计误差仍达40.56'，对准精度不高；IIR低通滤波法的对准效果要优于原始方法，它的对准结果虽然也呈现出波动，但相对于原始方法，波动的幅度较小，这是由于其采用了IIR低通滤波器对线运动干扰进行了抑制的缘故，但由于干扰频率介于通带和阻带的过渡段，其对准性能提高有限；本文方法在150 s时的方位对准精度收敛到10'以内，在对准结束时刻，方位对准精度为3.25'，这是因为本文方法受干扰频率的影响较小的缘故。

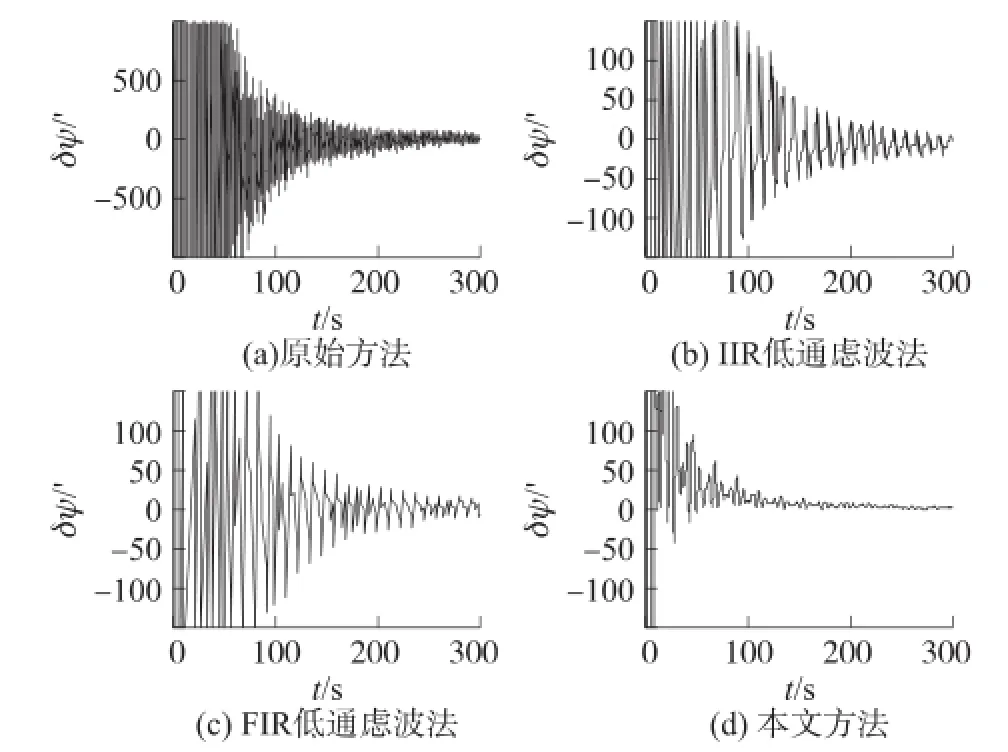
图3 角晃动与低频线运动干扰耦合情况下的对准误差

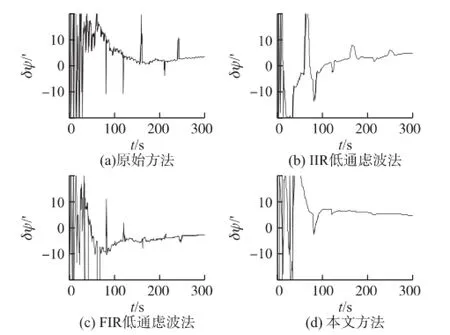
图4 角晃动与突变线运动干扰耦合情况下的对准误差

从图4可以看出，角晃动与突变线运动干扰耦合情况下（如由人员走动，开关车门等），原始方法的对准结果在突变干扰时刻附近出现跳动情况，对准误差的跳动幅度最大可达12'；IIR低通滤波法由于其频带限制，它不能彻底消除干扰，其对准误差也呈现出突变情况，但其突变幅度较原始算法较小；本文方法受突变干扰影响小，对准误差曲线相对于前两种方法更加平滑，这是因为本文算法对突变干扰采取了时域信号的处理方法，其不受干扰的频带限制，对于突变干扰具有平滑作用的缘故。从对准精度来看，3种算法在突变干扰消失后的方位对准误差均在3'附近，但在角晃动与突变线运动干扰耦合情况下，本文算法的对准精度优于其他两种方法。

5 结论

角晃动干扰与线运动干扰的耦合作用是SINS自对准的重要影响因素，本文将自对准问题转化为Wahba姿态求解问题，消除了角晃动干扰的影响；利用惯性系下的重力矢量信号的时域特性，用时域信号处理方法来实现消除线运动干扰，使得算法在两种干扰耦合的情况下依然能够精确快速地实现自对准。相对于基于频域的抗干扰方法，本文方法不受干扰信号频带特性限制，处理过程中信号不产生延迟，对低频线运动干扰和突变线运动干扰有更好的抑制能力。

［1］ 柏摇猛，李敏花.随机逼近自适应滤波在捷联惯导系统初始对准中的应用［J］.传感技术学报，2011，24（7）：1007-1010.

［2］ Acharya A，Sadhu S，Ghoshal T K.Improved Self-Alignment Scheme for SINS Using Augmented Measurement［J］.Aerospace Science and Technology，2011，15（2）：125-128.

［3］ 冯培德，李魁，王玮.一种新的舰载惯导系统摇摆基座初始对准方法［J］.仪器仪表学报，2012，33（1）：1-7.

［4］ 严恭敏，白亮，翁浚.基于频域分离算子的SINS抗晃动干扰初始对准算法［J］.宇航学报，2011，32（7）：1486-1490.

［5］ 吴枫，秦永元，周琪.基于重力矢量积分的SINS对准算法误差分析［J］.传感技术学报，2013，26（3）：361-366.

［6］ 秦永元，严恭敏，顾冬晴，等.摇摆基座上基于信息的捷联惯导粗对准研究［J］.西北工业大学学报，2005，23（5）：681-684.

［7］ Gu D Q，El-Sheimy N，Hassan T，et al.Coarse Alignment for Marine SINS Using Gravity in the Inertial Frame as a Reference ［C］//Position，Location and Navigation Symposium，2008 IEEE/ ION，Monterey，USA，May 5-8，2008.

［8］ 王跃钢，杨家胜，杨波.纬度未知条件下捷联惯导晃动基座的初始对准［J］.航空学报，2012，33（12）：2322-2329.

［9］ 孙枫，孙伟.基于数字滤波的系泊对准技术研究［J］.控制与决策，2010，25（2）：1870-1875.

［10］王跃钢，杨家胜.晃动基座下捷联惯导的抗干扰自对准算法［J］.控制与决策，2014，29（3）：1-4.

［11］练军想，汤勇刚，吴美平，等.捷联惯导惯性系动基座对准算法研究［J］.国防科技大学学报，2007，29（5）：95-99.

［12］Wahba G.A Least Squares Estimate of Spacecraft Attitude［J］.SIAM Review，1965，7（3）：409-411.

［13］严恭敏，白亮，赵长山，等.一种改进RLS算法及其在SINS快速对准中的应用［J］.宇航学报，2010，31（8）：1958-1963.

杨 波（1980-），男，汉族，江苏滨海人，第二炮兵工程大学自动控制系讲师，导航制导与控制专业博士，中国惯性技术学会会员，主要研究方向为惯性导航与组合导航、自主定位定向，yangbo8093@sina.com；

王跃钢（1958-），男，汉族，四川资中人，第二炮兵工程大学自动控制系教授、博导，精密仪器及机械专业博士，中国惯性技术学会理事，主要研究方向为导航制导与控制、导弹测试技术。

SINS Anti-Interrupt Self-Alignment Algorithm for Angular Swaying and Linear Motion Coupling Interference*

YANG Bo，WANG Yuegang，YANG Jiasheng，GUO Zhibin
（Department of Automation，The Second Artillery Engineering College，Xi'an 710025，China）

For the angular swaying and linear motion coupling interference，the strapdown inertial navigation system （SINS）is difficult to achieve alignment rapidly and accurately.In order to solve this problem，an anti-interrupt self-alignment algorithm for angle swaying motion and linear motion coupling interference is presented.In this algorithm，the alignment problem is transformed into the Wahba problem to remove the angular swaying interference，and timedomain signal processing methods are used to remove the linear motion interrupt according to the time-domain characteristics of the gravity vector signal in inertial reference frame.The simulation results show that，the presented method can accomplish alignment quickly in the presence of the angular swaying and linear motion coupling interference.

strapdown inertial navigation system；anti-interrupt self-alignment；Wahba problem；time-domain signal processing；angular swaying；linear motion；coupling interference EEACC：6330；7230

V249.3

A

1004-1699（2015）04-0526-05

10.3969/j.issn.1004-1699.2015.04.013

项目来源：武器装备预研项目（EP111015）

2014-11-09 修改日期：2014-12-29