一种改进小波阈值函数的光纤光栅传感信号去噪方法*

曹京京，胡辽林，赵 瑞

（西安理工大学机械与精密仪器工程学院，西安 710048）

一种改进小波阈值函数的光纤光栅传感信号去噪方法*

曹京京，胡辽林*，赵 瑞

（西安理工大学机械与精密仪器工程学院，西安 710048）

光纤布拉格光栅（FBG）传感信号中存在的噪声严重影响了其中心波长的检测精度，因此必须进行去噪处理。本文针对传统的小波软、硬阈值函数去噪的不足，提出了一种改进的对数阈值函数，并确定了最优的小波基和分解尺度。仿真表明，本文提出的改进阈值函数去噪后信噪比（SNR）较大，均方根误差（RMSE）较小，其中信噪比比传统的软、硬阈值方法提高了1.5 dB～4 dB。最后通过实验验证了本文方法的去噪效果。

光纤光栅；去噪；小波；阈值函数；信噪比

光纤布拉格光栅（FBG）传感器广泛应用于应变、温度、压力、磁场等多种物理量的测量，其原理是通过检测 FBG的波长漂移来测量物理量的变化［1-2］。FBG传感信号在采集和传输的过程中易受噪声干扰，会影响反射谱中心波长的准确定位，对精确测量被测物理量变化带来了困难。因此必须对FBG传感信号进行去噪处理［3-5］。

经典的数字滤波去噪，如有限脉冲响应滤波器，主要是基于频域的处理方法，用这种方法把信号和噪声分开的一个重要前提是信号频谱和噪声频谱没有重叠；但实际情况往往相反，噪声的频谱几乎分布在整个频域内，此时数字滤波去噪效果较差［6］。而小波变换具有良好的时频分析和多分辨率特性，能有效区分非平稳信号中的突变部分和噪声，在提高信噪比的同时保持对突变信息的良好分辨能力［7-8］。1994年，Donoho等人提出了小波阈值去噪的概念，并证明了该方法能够在最小均方差意义下得到最优估计值［9］。传统的小波阈值去噪包括软阈值和硬阈值去噪，但它们都存在一些缺陷。硬阈值函数存在间断点，去噪过程会出现附加振荡，软阈值函数虽然连续，但得到的估计信号与原信号存在恒定偏差［10-12］。对此，一些学者提出了改进的阈值算法，文献［7］提出的改进阈值函数具有较好的连续性，但存在不确定因子，其取值的变化影响去噪效果。

针对上述方法存在的缺陷以及FBG信号的特点，本文提出了一种基于对数的改进阈值函数。该阈值函数具有连续性，且能克服软阈值函数的恒定偏差问题。通过MATLAB仿真选取了合适的小波基和分解层数，并对含噪的FBG仿真信号进行了去噪处理，结果表明了本文提出的方法去噪效果良好，最后通过实验对仿真结果进行了验证。

1 小波阈值去噪的基本原理

假设有一维观测信号

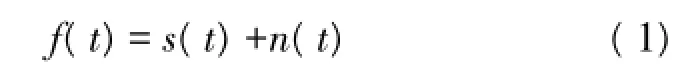
式中：f（t）为含噪信号，s（t）为原始信号，n（t）是方差为σ2、服从N（0，σ2）分布的高斯白噪声。首先对f（t）做离散小波变换，得到j尺度下k点位置的小波变换系数ωj，k。小波变换后，信号的能量分布在极少的小波系数上，且系数幅值较大，而噪声能量较均匀地分布在整个小波域中，并且对应的小波系数幅值较小。通过在不同尺度上选取一个合适的阈值，并将小于该阈值的小波系数置零，而保留大于阈值的小波系数，得到阈值量化后的小波估计系数 ^ωj，k，再通过小波逆变换重构去噪后的信号，达到去噪目的。

2 改进的小波阈值函数

阈值函数关系到重构信号的精度和连续性，影响小波去噪的效果，传统的阈值函数包括硬阈值函数和软阈值函数。式（2）为硬阈值函数，式（3）为软阈值函数［13］。

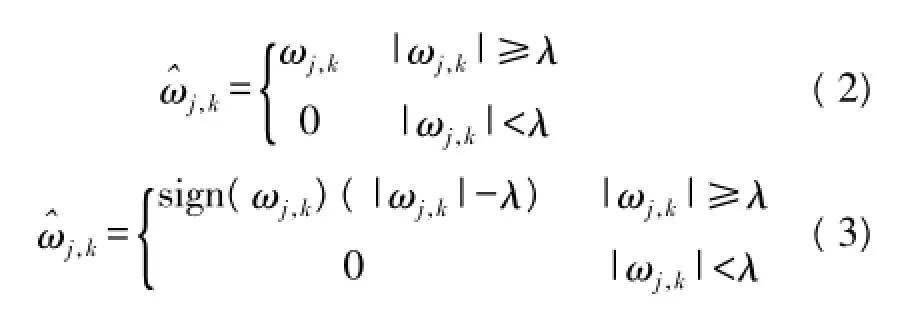
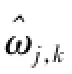
为了克服软、硬阈值函数的缺点，必须寻求新的阈值函数，新的阈值函数应该具备在阈值点处连续，且当|ωj，k|增大时，j，k必须趋近于ωj，k。根据上述分析，提出一种新的阈值函数

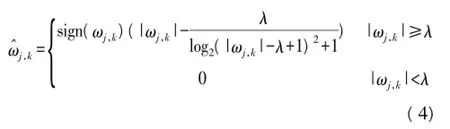
3 基于改进阈值函数的小波去噪仿真

3.1 FBG反射信号

光栅反射谱由光纤模式耦合理论得到，光电探测器探测到的FBG反射谱的光功率为［14］

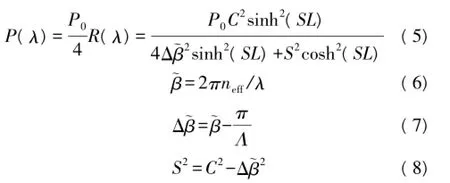
式中：P0是光源输出的光功率，R（λ）是光纤光栅反射率，~β为传输常量，Δ~β是传输常量的失谐量，C为耦合系数，L是光栅长度，neff为纤芯有效折射率，Λ为光栅周期。

由式（5）所得的无噪 FBG反射谱信号如图1（a）所示。在图1（a）上叠加均值为0、标准差为0.02高斯白噪声，产生含噪的 FBG反射谱，如图1（b）所示。

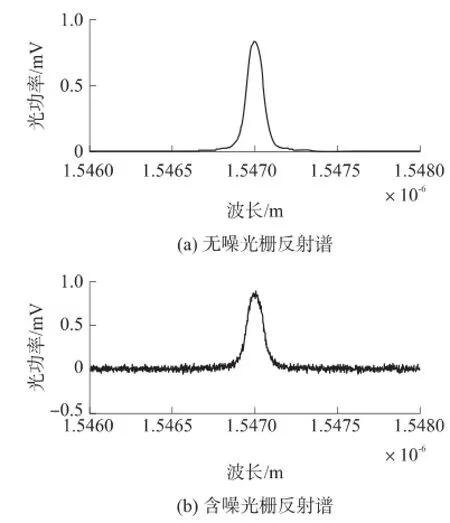
图1 FBG反射谱

3.3 阈值的选取

阈值的选取是小波阈值去噪的另一个关键问题，若选取的阈值过大，会将部分有用信号当作噪声滤除；若选取的阈值过小，则噪声去除不完全，影响滤波效果。Donoho等人提出了常用阈值表达式

式中：σ为噪声的均方根误差，N为信号的长度。由式（9）可以看出，一旦信号给定，阈值便为一个确定的值，但是随着分解尺度的增加，噪声的小波系数逐渐减小，因此本文采用改进的阈值［15-16］

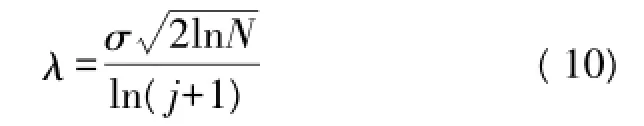
式中：j为分解尺度。由式（10）可以看出，当分解层数增加、噪声的小波系数减小时，阈值相应减小。

3.4 小波基和分解层数的选取

不同的小波基对含噪信号的去噪效果不同，根据FBG信号的特点，我们选择由Daubechies提出的具有近似对称性的正交Symlets小波基。本文对含噪FBG信号进行基于不同小波基去噪处理时，信号的分解层数、阈值函数以及阈值保持不变。以信噪比的变化作为基准，来确定小波基的最佳阶数。去噪后信号的信噪比随小波基阶数的变化如图2所示。可以看出，选取Sym8小波基时，相比于同族其他小波基信噪比达到最大，因此选用Sym8小波基。

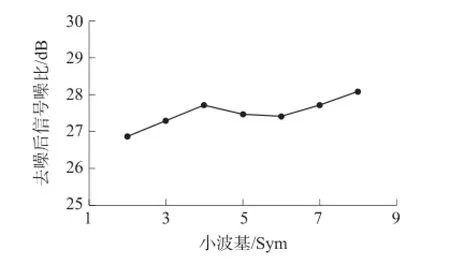
图2 信噪比随小波基的变化

信号的分解层数越大越有利于信噪的分离，但对于重构来说，分解层数越大则重构误差越大。本文依据信噪比与分解层数的关系来确定合适的分解层数。本次仿真选用Sym8小波基，并保证阈值函数和阈值不变。结果如图3所示，可以看出，当分解层数逐渐增大时，信噪比先逐渐增大，当分解层数为5时达到最大，此后开始减小。因此我们选择的分解层数为5层。

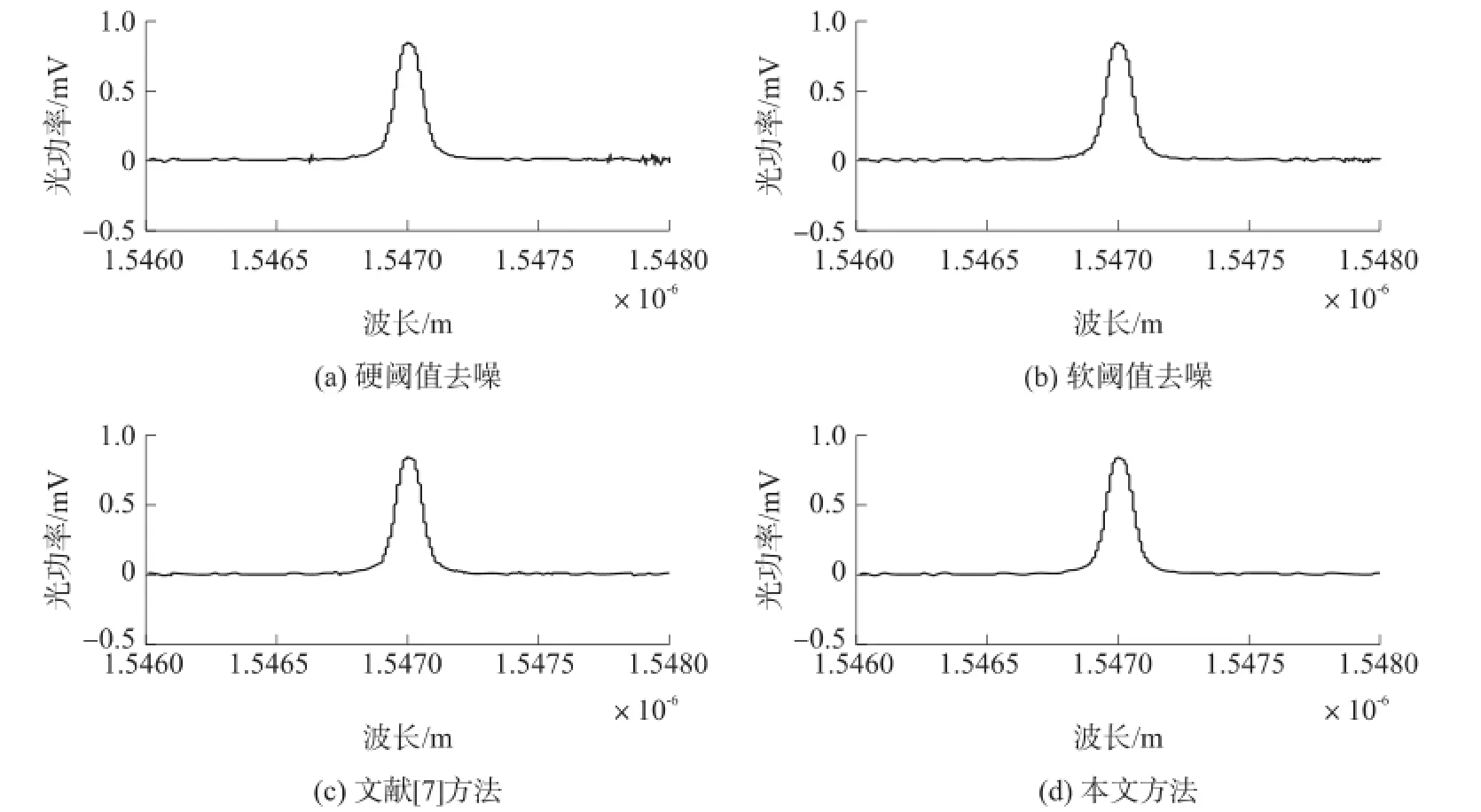
图4 不同方法去噪效果图

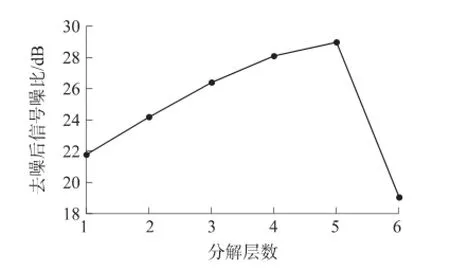
图3 信噪比随分解层数的变化

3.5 去噪效果

我们选用sym8小波基，且分解层数为5，对图1（b）所示的含噪FBG信号分别用硬阈值函数、软阈值函数、文献［7］提出的阈值函数、以及本文提出的阈值函数进行去噪处理，去噪效果如图4所示。

从图4可以看出，本文提出的改进阈值函数去噪效果较好；文献［7］提出的阈值函数存在不确定因子，因此去噪后的信号仍留有微量噪声，去噪效果次之；软阈值函数存在恒定偏差，对重构信号产生了误差，因而去噪效果较差；硬阈值函数的不连续性使得去噪效果最差。

一般选用信噪比（SNR）和均方根误差（RMSE）来评价各种去噪方法的优劣。当 SNR值越大，RMSE的值越小时，表明去噪效果越好。其定义式分别为

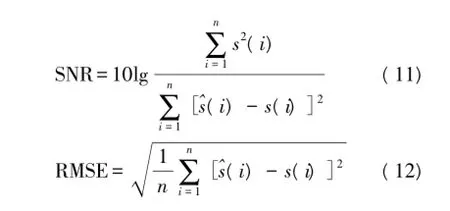
对上述4种方法去噪效果的评价如表1所示，可以看出，本文提出的改进阈值去噪算法信噪比最大（33.422 dB），均方根误差最小（3.819×10-3），说明本文提出的方法优于其他方法，与图4得出的结论相符。

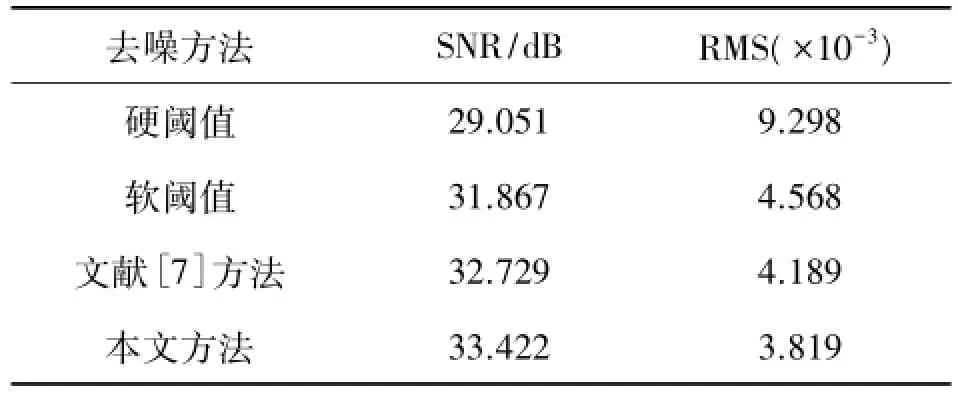
表1 不同方法去噪的SNR和RMS

4 实验验证

FBG传感信号采集系统框图如图5所示，选用放大自发辐射宽带光源作为系统光源，光通过隔离器进入耦合器，再进入FBG，反射光波通过耦合器进入光谱仪，同时使用计算机通过通用接口总线（GPIB）控制光谱仪，采集和记录数据。实验中设置的中心波长为1 549.9 nm，扫描范围为2 nm，采集到的含噪信号如图6所示。

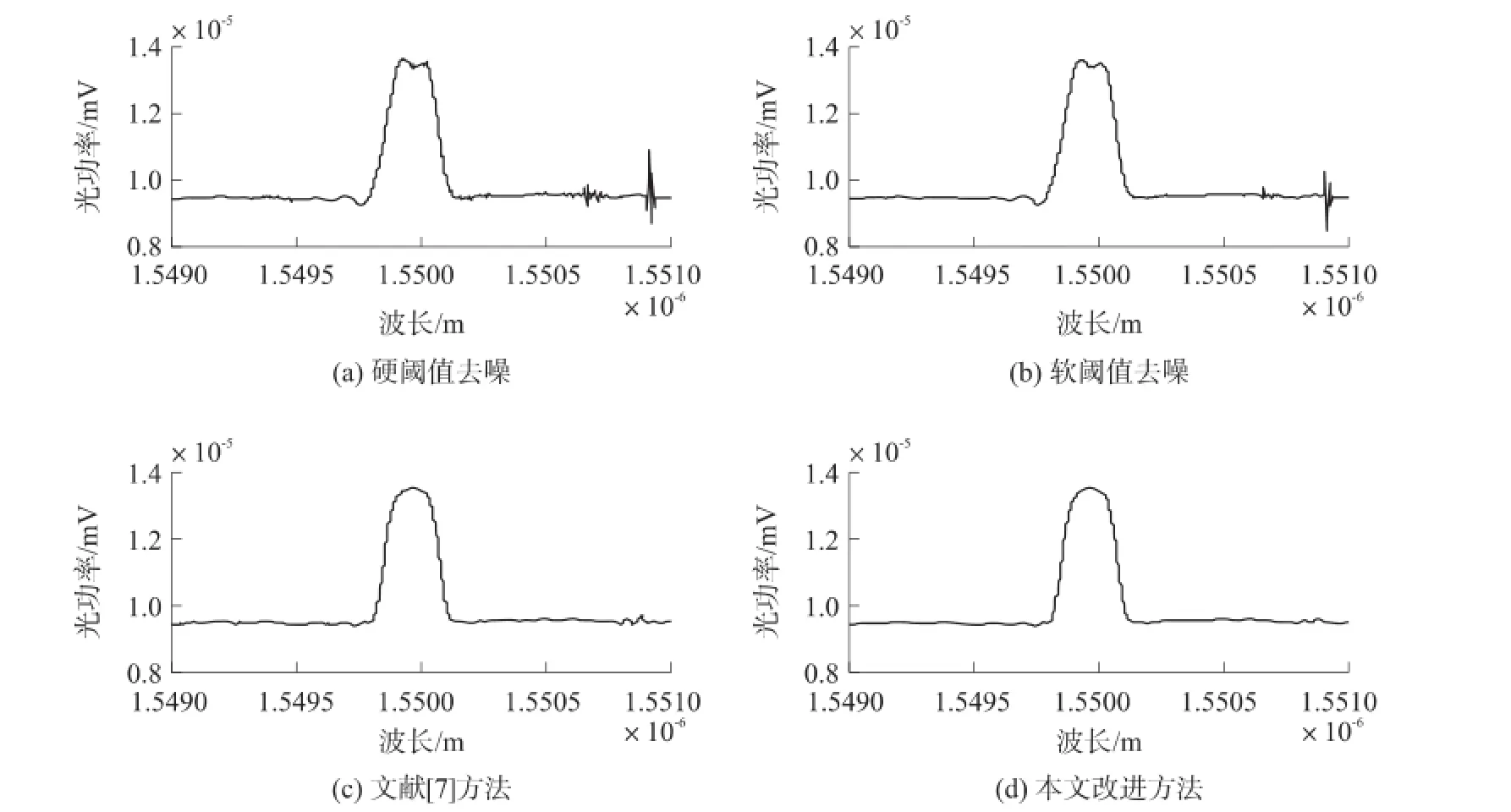
图7 不同方法去噪效果图

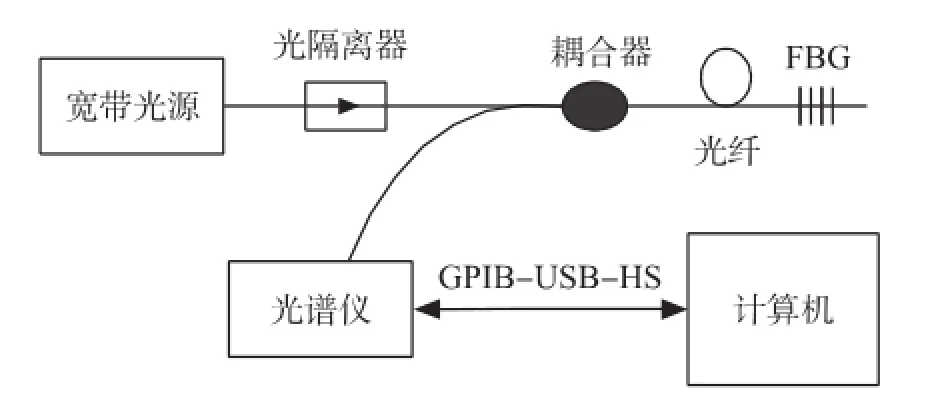
图5 FBG传感信号采集系统框图

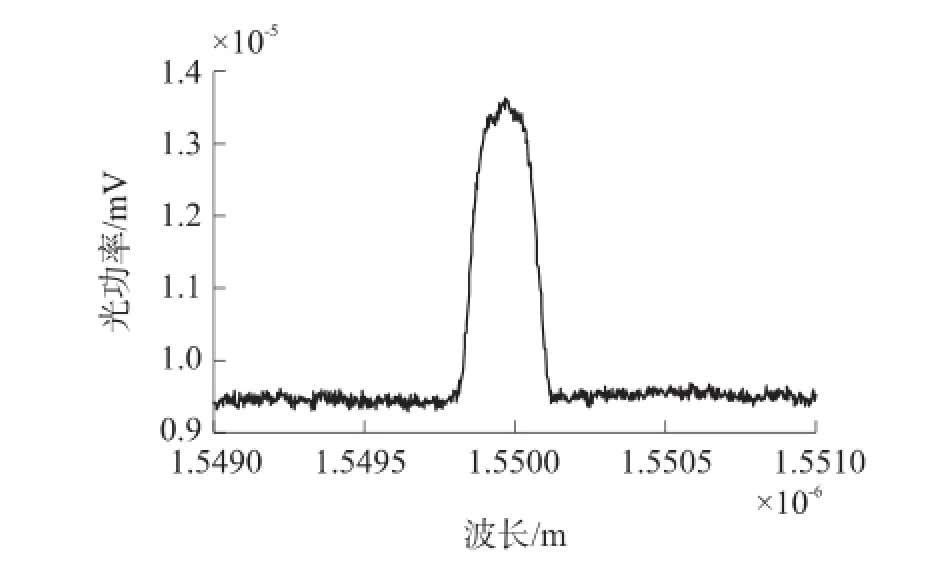
图6 含噪的FBG实验反射谱

对实验测得的含噪FBG实验反射谱分别用硬阈值函数、软阈值函数、文献［7］提出的阈值函数、以及本文提出的阈值函数进行去噪处理。同样选取Sym8小波基，分解尺度为5层，阈值为式（12）所示的改进阈值，去噪效果如图7所示。

由图7可以看出，本文提出的改进阈值函数去噪效果最优；文献［7］提出的阈值函数去噪后的信号仍留有少量噪声，去噪效果次之；软阈值存在恒定偏差，去噪效果较差；硬阈值函数的不连续性使得去噪效果最差。由此可见，实验数据的去噪效果与仿真数据去噪效果一致，证明了本文提出的改进方法具有一定的优越性。

5 结论

本文针对软、硬小波阈值函数存在的一些缺陷，以及文献［7］改进小波阈值函数因存在不确定因子而影响去噪效果的不足，提出了一种连续且稳定的对数小波阈值函数，并通过MATLAB仿真确定了最优的小波基和分解层数。对FBG仿真信号进行去噪处理，发现采用本文改进的小波阈值函数去噪后，信号能够获得最大信噪比以及最小均方根误差。通过实验验证，证明了本文的改进方法具有较高的实用价值。

［1］ David Barrera，Vittorria Finazzing，Joel Villatoro，et al.Packaged Optical Sensor Based on Regenerated Fiber Bragging Gratings for High Temperature Applications［J］.IEEE Sensor Journal，2012，12（1）：107-112.

［2］ 胡辽林，章鹏博，华灯鑫，等.时分复用光纤光栅传感阵列中DFB激光器的高精度温控设计［J］.传感技术学报，2012，25（7）：921-925.

［3］ 王亚萍，胡辽林，张卫超.分布式光纤光栅传感系统中微弱信号检测研究［J］.西安理工大学报，2013，29（4）：88-94.

［4］ 胡辽林，张卫超，华灯鑫，等.基于LabVIEW的光纤光栅传感的动态解调［J］.计算机应用，2013，33（5）：1473-1475.

［5］ 侯立群，赵雪峰，冷志鹏，等.光纤光栅应变传感温度器温度补偿计算值的改进［J］.传感技术学报，2014，27（1）：70-73.

［6］ 王香云.基于FPGA的小波去噪的硬件实现［J］.激光技术，2013，37（6）：786-790.

［7］ 徐洁，宋英，刘功检，等.基于平移不变小波变换的脑电信号去噪［J］.济南大学学报，2014，28（3）：209-214.

［8］ 何玉钧，王梓蒴，尹成群，等.利用平稳小波变换处理FBG传感信号［J］.红外与激光工程，2011，40（11）：2295-2300.

［9］ 邵鸿翔，高宏峰.改进小波阈值去噪方法处理FBG传感信号［J］.激光与红外，2014，44（1）：73-76.

［10］高国荣，刘艳萍，潘琼.基于小波域可导阈值函数与自适应阈值的脉冲星信号消噪［J］.物理学报，2012，61（13）：139701.

［11］CHANG Fengxiang，HONG Wengxue，ZHANG Tao.Research on Wavelet Denoising for Pluse Signal Based on Improved Wavelet Thresholding［C］//First International Conference on Pervasive Conputing，Signal Processing and Applications，2010：564-567.

［12］杨恢先，王绪四，谢鹏鹤，等.改进阈值与尺度间相关的小波红外图像去噪［J］.自动化学报， ，37（10）：1167-1172.

［13］陈晓曦，王延杰，刘恋.小波阈值去噪法的深入研究［J］.激光与红外，2012，42（1）：105-110.

［14］吴朝霞，吴飞.光纤光栅传感原理及应用［M］.北京：国防工业出版社，2011，29-30.

［15］陈勇，贺明玲，刘焕淋，等.利用改进阈值平移不变量小波处理FBG传感信号［J］.光电子·激光，2013，24（2）：246-252.

［16］Abdourrahmane M Atto，Dominique Pastor，Grégoire Mercier.Wavelet Shrinkage：Unification of Basic Thresholding Functions and Thresholds ［J］.Signal，Image and Video Processing，Springer，2011，5（1）：11-28.

曹京京（1991-），女，西安理工大学在读硕士生，研究方向为光纤传感技术，cjingjing08@163.com；

胡辽林（1968-），男，西安理工大学副教授，博士，主要研究光纤传感及光纤通信，huliaolin@163.com。

Improved Threshold De-Noising Method of Fiber Bragg Grating Sensor Signal Based on Wavelet Transform*

CAO Jingjing，HU Liaolin*，ZHAO Rui
（School of Mechanical and Precision Instrument Engineering，Xi'an University of Technology，Xi'an 710048，China）

Noise in the fiber Bragg grating（FBG）sensing has seriously affected the detection precision of the center wavelength，and it should be processed to reduce noises.A modified logarithmic threshold method is adopted，and the reasonable wavelet basis and decomposition level are determined by analyzing the disadvantages of traditional soft and hard wavelet threshold de-noising methods.The simulation results show that the improved method can obtain the maximum signal-to-noise ratio（SNR）and the minimum root mean square error（RMSE），and the SNR improves 1.5 to 4 dB than traditional methods.The de-noising effect of this method is proved by experiments.

fiber Bragg grating；de-noising；wavelet；threshold function；signal-to-noise ratio

TN929.11

A

1004-1699（2015）04-0521-05

7230

10.3969/j.issn.1004-1699.2015.04.012

项目来源：陕西省自然科学基金项目（2014JM7273）

2014-11-10 修改日期：2015-01-16