基于SIMULINK的单神经元自适应PID控制器研究
杜晓婷,方飞
(安徽三联学院电子电气工程学院,安徽合肥 230061)
基于SIMULINK的单神经元自适应PID控制器研究
杜晓婷,方飞
(安徽三联学院电子电气工程学院,安徽合肥 230061)
本文分析了单神经元自适应PID控制器结构,给出了基于有监督的Hebb学习规则的算法模型,在此基础上做出改进,建立了神经元自适应控制器SIMULINK仿真模型,并对被控对象进行仿真研究.
PID控制器;单神经元;SIMULINK
1 引言
神经元指的是神经网络中最小的处理单元,单个的神经元处理信息功能较为单一,一般只应用于一些简单的信息处理.而传统的PID控制器虽然结构简单,控制直观,使用方便,但需要建立在具有非常精确的数学模型的确定系统之上.如果将单个的神经元与传统的PID控制器相结合,便可实现复杂系统控制以及时变系统控制,称为单神经元自适应PID控制器.其控制效果较传统的PID控制器优越.
2 单神经元自适应PID控制器结构图
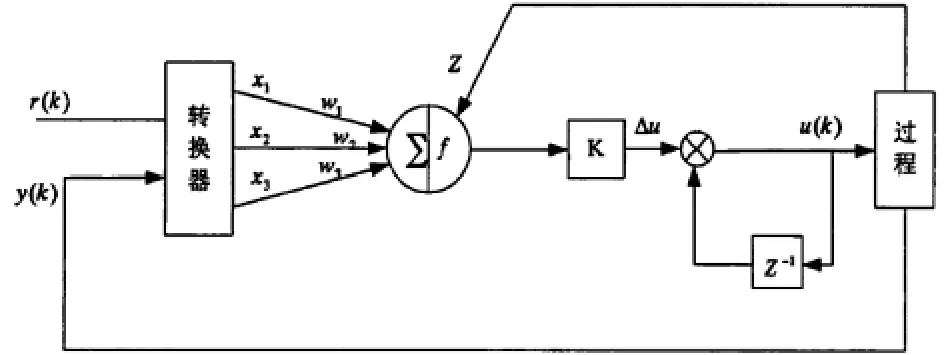
图1 单神经元自适应PID控制器结构图
单神经元自适应PID控制器结构图如图1所示[2-3],图中,r(k),y(k)分别为转换器的输入量和控制器的输出量,神经元学习中需要的状态量,从转换器的输出端输出,分别用x1、x2、x3表示,也称为单神经元的输入,K表示神经元的比例系数[1].
神经元自适应控制器的输出为:

式中,ωi(k)是与xi(k)相对应的权系数,
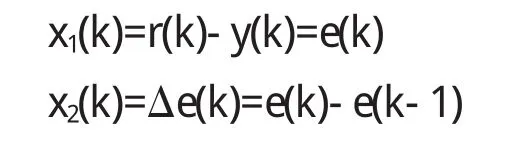

与增量式算法相比较,神经元自适应控制器中的加权系数ωi(k)与增量控制算法中预先设定好的系数不同,通过自学习功能,ωi(k)的值可以进行自适应调整.
3 有监督的Hebb学习规则
本文采用有监督Hebb学习算法,有:

有监督的Hebb学习算法规范法处理后为:

式中,ηi为积分学习效率,ηp为比例学习效率,ηd为微分学习效率.
由以上公式可知,这种单神经元控制算法可以看做为可变参数的自适应PID控制.
在此基础上进行改进,即将上式中的xi(k)用e (k)+Δe(k)替换,如下所示:
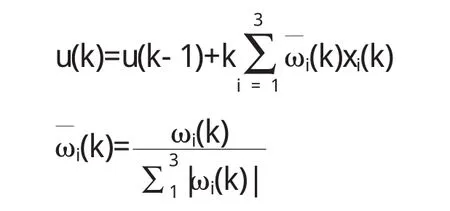
其中,
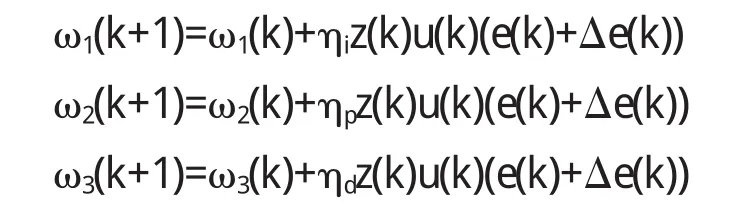
式中,Δe(k)=e(k)-e(k-1),z(k)=r(k)-y(k)=e(k).改进后的Hebb学习算法,加权系数便可以根据实际经验值进行修正.
4 SIMULINK仿真实现
工业生产过程中,被控对象具有普遍性和典型性的特点,因此,采用广义对象传递函数:

设采样时间ts=1s,经过Z变换后的对象为:

神经元自适应控制器SIMULINK仿真模型如图2所示:

图2 单神经元自适应PID控制器仿真模型
5 仿真结果分析
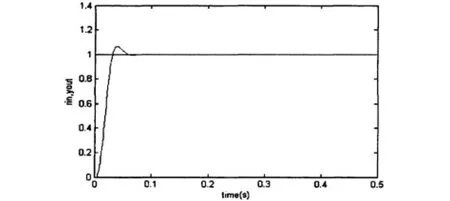
图3 改进的Hebb学习规律阶跃跟踪曲线图
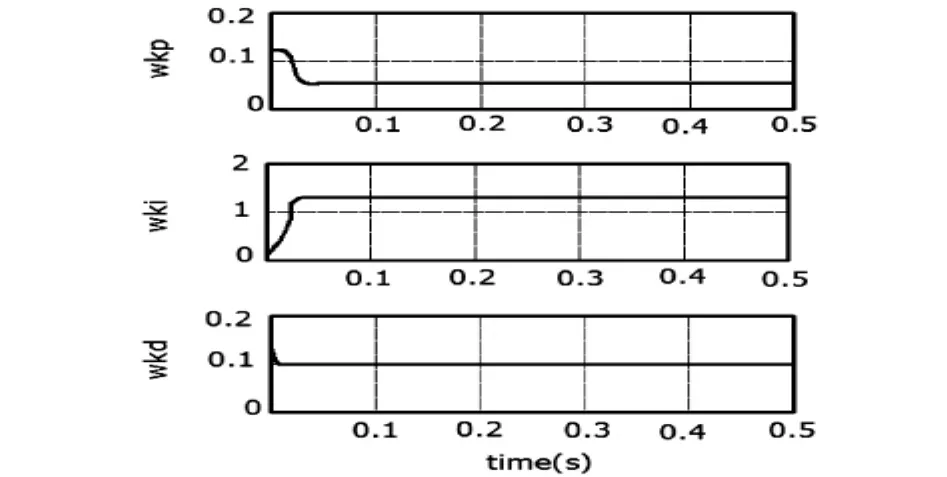
图4 改进的Hebb学习规律权值变化曲线图
在单神经元自适应控制器仿真中,令ωp=ωi=ωd0.1,ηp=0.4,ηi=0.35,ηd=0.4,比例系数K=0.06,ts=1ms,改进的Hebb学习规律阶跃响应曲线图如图3-4所示.
6 对外部对象发生变化时的适应性(鲁棒性)
在工业控制过程中,如果受到某种外界因素的干扰,便可考验控制器的自适应能力.当对象模型发生变化时,单神经元自适应控制器的自适应效果明显.
设K0:1.5-2.5;τ:3-6,T2:2.35-8,此时的控制对象为:

单神经元自适应PID控制器对外部对象发生变化的适应性曲线如图5所示:
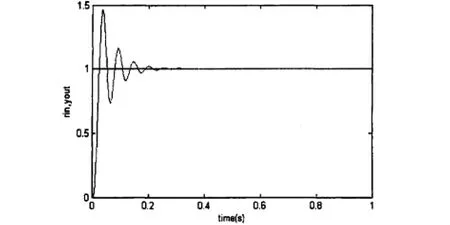
图5 基于改进Hebb学习规律的对外部对象发生变化时的适应性
由以上仿真结果可以看出,单神经元自适应控制器的上升时间,超调量以及调节时间与传统的PID控制器相比,均得到了明显的改善,自适应能力较强,控制效果较优越.
〔1〕刘金琨.先进PID控制matlab仿真(第三版)[M].北京:电子工业出版社,2011.
〔2〕舒迪前,李春涛,尹怡欣.单神经元自适应PID控制器及其在电加热炉上的应用[J].电气传动,1995,25(1):29-32.
〔3〕A.J.Calise,N.Hovakimyan and M.Idan.Adaptive outputfeedbackcontrolofnonlinersystems using neural networks[J].Autmatic,2001,37(8):1201-1211.
TP273
A
1673-260X(2015)04-0016-02
本文基于安徽三联学院院级自然科学研究项目(2014Z014)

