化学建模与模型集群分析

云永欢　邓百川　梁逸曾

摘 要 本文简单介绍了化学建模与模型集群分析的思想，并列举了基于模型集群分析的思路与框架。近年来，应用于化学建模各个方面的许多新算法包括奇异样本诊断、变量选择、模型参数与评价、稳健与模型应用域。本文通过应用于不同的数据类型，包括近红外光谱、定量构效关系及代谢组学数据，举例阐述模型集群分析方法的可行性与应用性，为未来开发化学建模新算法提供一个好的思路和框架。

关键词 化学建模； 模型集群分析； 采样； 统计分析； 综述

1 引 言

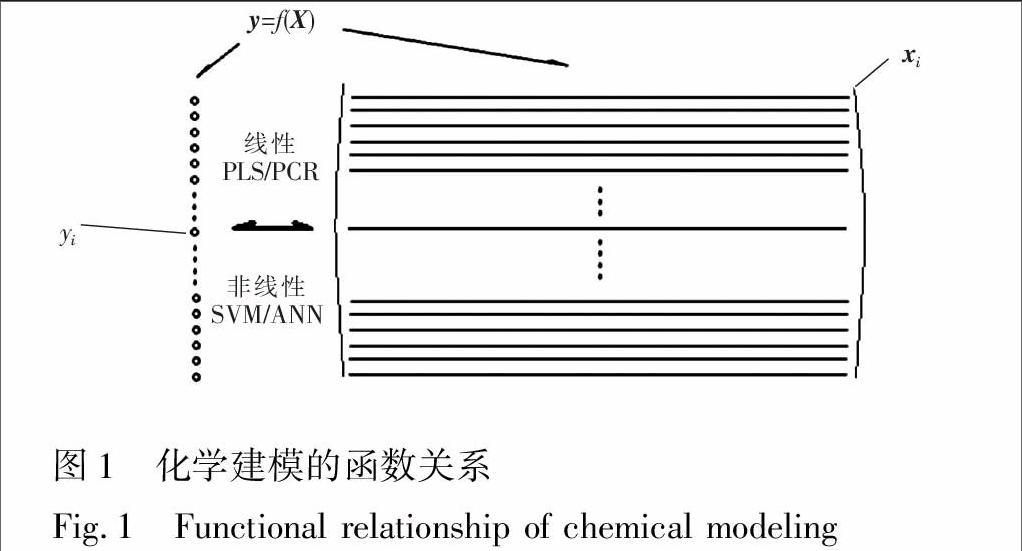
随着化学量测数据的不断累积和大数据信息处理技术，包括数据发掘和机器学习各种新方法的不断涌现，采用化学建模（Chemical modeling）方法进行化学知识规律发现及建立定量模型等研究得到了飞速发展。此外，在分析化学的发展过程中，由于仪器分析的飞速发展，复杂体系的快速仪器分析，包括近红外和拉曼光谱无损分析及各类波谱如质谱、激光诱导击穿光谱（LIBS）等的分析、代谢组学中核磁共振谱及各种色谱分析、中药色谱指纹图谱分析等，现都已成为了分析化学的重要研究方向[1]。值得提出的是，这样的化学建模的共同特点是它们的模型都可由下述简单算式给出： y=f（X）。式中， y为含n个元素的列矢量，每个元素都表征一个样本的定性特征或定量指标，而矩阵X则为含n行的矩阵，每行为一系列表征样本属性特征（含p个元素）或一个样本的测量谱（波谱或色谱）； f（.）为不定的函数关系，它可以是线性的，如主成分回归（PCR）或偏最小二乘（PLS）；也可以是非线性的，如支撑向量机（SVM）或人工神经网络（ANN）等。其关系见图1。

由图1可见，此类数据体系（包括紫外、近红外、拉曼光谱分析、定量构效关系和代谢组学数据）是一类极具复杂性的体系，由于其函数关系f（.）是未知的，线性或非线性无法确定，变量与y的关系不明确，没有任何物理或化学定理可作为基础，解空间类似美国著名统计学家George E. P. Box所说的那样，即“所有模型都是错误的，但其中有些是有用的（All models are wrong， and some are useful.）”。所以，对于这样的复杂体系，找到尽量逼近的基空间，并通过有效模型评价方法及其可靠应用域的定义方法十分重要。

近年来，化学与生物领域引入大量高通量分析技术，使得上述模型中的 xi 这个行矢量变得很长，而且其中还有很多变量与yi无关，甚至还有干扰作用[2～5]。此外，由于目前样本数（n）相对较少，出现了在统计学称为维数灾祸的“大p，小n”问题，这是目前统计学及其应用领域研究的重大挑战[6～8]。对于这样的体系，很容易出现模型过拟合，建模须谨慎[9，10]。

2 化学建模与模型集群分析

化学计量学和化学信息学研究的一个主要目标就在于建立一个有效并可靠的化学模型，以对未知的化学样本的浓度/性质等进行预测。从上述的分析可知，这个任务不简单，由于模型完全未知，建模有点类似“瞎子摸象”的任务。而模型集群分析（Model population analysis，MPA）[9，11] 打破传统一次性建模思路，力求最大限度地利用已有样本集的信息，通过随机采样，从不同角度考察数据集的内在性质，通过对所得结果进一步统计分析，获得数据集的内在结构。从这个角度看来，模型集群分析与贝叶斯统计分析的追求后验分布有些类似。而且，模型集群分析中主要是强调集群分析，强调所得的各种不同结果的分布，与一次性建模分析形成了强烈对比。

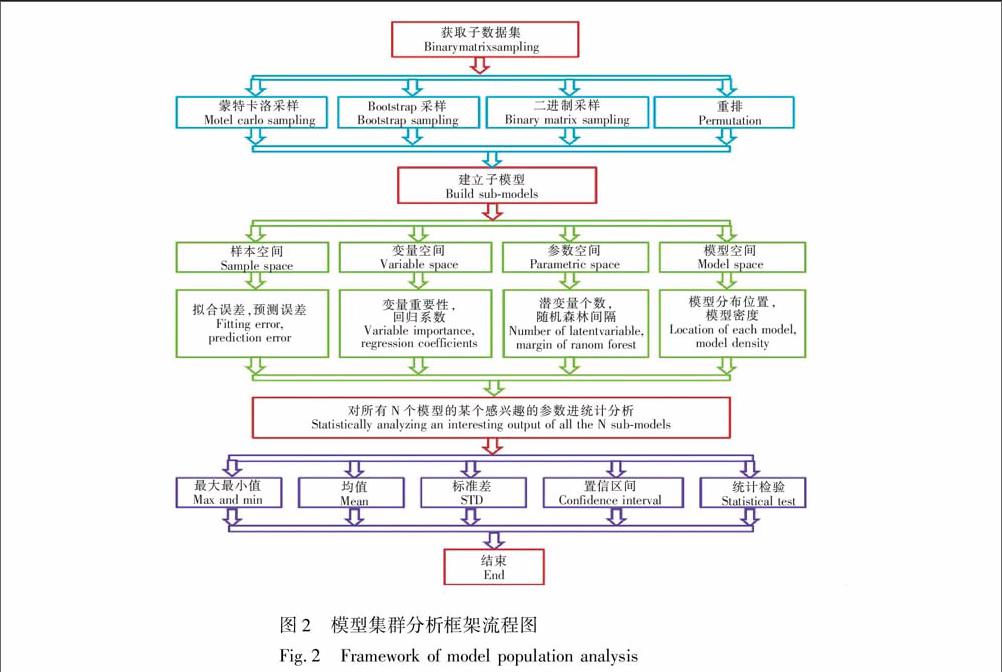
基于模型集群分析的化学建模算法之构建框架示于图2。它的构建框架主要包括3个基本要素：（1）通过随机采样获取子数据集；（2）针对每个子数据集，建立一个子模型；（3）从样本空间、变量空间、参数空间或模型空间对所有建立的集群子模型的感兴趣的参数进行统计分析，获取有用的信息。

3 模型集群分析的3个基本要素

3.1 随机采样获取子数据集

采样是数据进行统计分析中常用的有力工具[12]。通过随机采样，可以从给定一个数据集的样本或变量空间中获取N个子数据集。如果从样本空间获取，子数据集由部分样本组成，从变量空间获取，则子数据集由部分变量组成； 如果同时从样本和变量空间获取，子数据集则由选取部分样本和部分变量组成。目前，应用于MPA中常用的随机采样方法有4种：（1）蒙特卡洛采样（Monte Carlo sampling）[13]、（2）自助法采样（Bootstrap sampling）[14]、（3）二进制采样（Binary matrix sampling）[15～19]、（4）重排技术（Permutation）[20]。

蒙特卡洛采样，无放回采样，也称刀切法（Jack knife），随机选取一定比例的样本作为训练集，剩下的样本作为独立测试集。

自助法采样，有放回采样，每个样本被选中的概率相同，因此会出现有些样本被多次选中，这些样本可作为重复样本，也可以一次使用。随机性选取一定比例的样本作为训练集，其余的样本为独立测试集。

二进制采样是新近提出的一种采样方法，首先产生二进制矩阵，行代表采样次数，列代表对应数据的变量，矩阵只是含0和1，0代表变量被选中，1代表变量没被选中，每一列0和1的比例统一设定，接着每一列自主打乱，根据每行有1的位置选取变量，由于每列1的数目是固定的，这种方法能够保证按行选取变量时，变量被选择的概率相同。

重排技术是对样本矩阵或响应值矢量进行重排打乱，然后再建模，普遍应用于检查过拟合风险。

3.2 建立子模型

对所有产生的N个数据集，采用选定的建模方法建立模型，将得到N个子模型。由于每个子模型是建立在相对应的子数据集上，仅反映了原数据集的局部信息，建立N个子模型可较全面地反映原始数据集的信息。目前比较常用的建模方法有线性方法和非线性方法。（1）线性方法包括多元线性回归（MLR）、偏最小二乘（PLS）、主成分回归（PCR）、岭回归（RR）、Lasso回归、线性判别分析（LDA）；（2）非线性方法包括支撑向量机（SVM）、神经网络（ANN）、分类回归树（CART）、随机森林（Random forest）。endprint

3.3 统计分析

MPA的核心思想是对获得的由N个子模型构成的集群模型的某个感兴趣的参数进行统计分析，通过统计分布获取对解决实际问题有价值的信息。实际上，由于应用的复杂性与多样性，对感兴趣的参数进行统计分析的策略需要根据具体情况进行具体分析与设计，不同的策略与设计将会产生不同的算法。而这些对所有建立的集群子模型的感兴趣的参数是从样本空间＼，变量空间＼，参数空间或者模型空间4个空间获取的。样本空间：与样本相关的模型输出，如回归模型里样本的拟合误差，预测误差；分类模型里，样本类别的预测准确率。变量空间：与变量相关的模型输出，如变量的回归系数。参数空间：与模型自身相关的参数，如PLS模型主成份的个数，随机森林与支撑向量机模型的间隔。模型空间：模型相对于其它模型的参数，是由集群模型共同决定，如模型在空间的位置＼，模型的分布密度。

继通过统计分布分析所有建立的集群子模型的感兴趣的参数，如：（1）对正常样本与奇异样本的两类预测误差分布诊断奇异样本；（2）不同的变量组合的交互检验预测误差分布来找出最优的变量子集；（3）比较某个变量组合中某个变量存在和不存在模型里时的两个交互检验预测误差分布来获得变量重要性；（4）比较每个变量被重排前后的预测误差分布来获得每个变量的重要性。

针对这些分布，利用其最大最小值、均值、标准差、均值标准差比、95%置信区间、t检验（有参数检验）和Mann-Whitney U检验[21]（无参数检验）获得有价值的信息。4 基于MPA的新算法在化学建模中的应用

MPA是基于建立集群模型的一种数据分析思路。它是数据分析的一般性框架，为系统研究数据结构、建立模型及算法设计等提供了新的思维方式。基于MPA的3个基本要素和4个空间，近来已经开发了应用于化学建模的许多新算法，包括奇异样本诊断、变量选择、模型参数与评价、稳健与模型应用域。下面对化学建模的这几个方面的应用进行简单举例介绍。

4.1 奇异样本诊断

构建稳健的化学模型主要取决于训练集数据样本。如果训练集数据中包括一些远离数据主体的奇异样本，它们将会破坏整个数据结构，从而影响模型的建立以及预测。因此，奇异样本诊断是稳健化学建模的一个关键步骤[22]。Cao等[23]提出的基于模型集群分析的奇异样本诊断方法（Monte Carlo sampling， MCS）主要研究了基于模型特征分布诊断奇异样本，其步骤如下：（1）采用蒙特卡洛采样从原始数据总样本中选取一定比列的样本作为训练样本，如r=80%，剩下的20%样本作为独立测试集样本。这个过程重复N次，即可得到N个子训练集和与之对应的N个子测试集；（2）每个子训练集建立模型并对相应的测试集样本进行预测；（3）设每个样本被等概率采样，则其被选进测试集的次数接近N（1-r）。因此，每个样本将约有N（1-r）个预测误差，其预测误差的统计分布特征可用于诊断奇异样本。

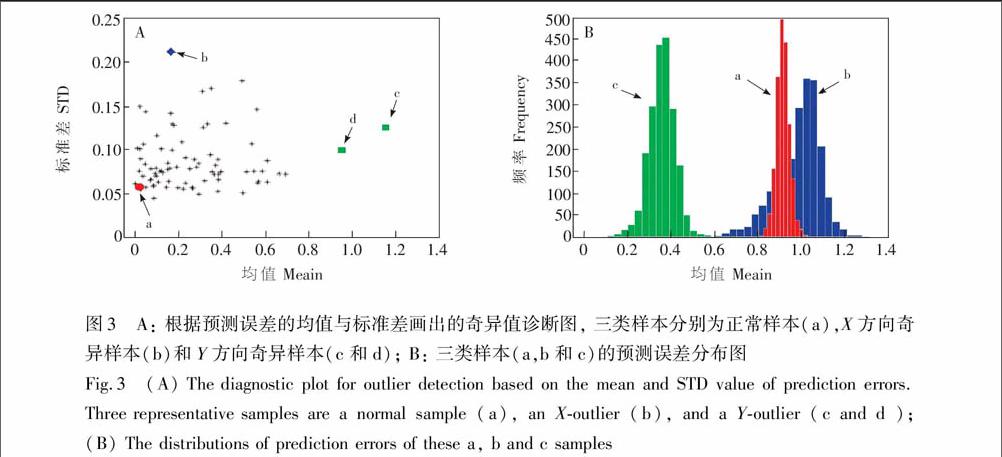
举一个使用MCS方法诊断奇异样本的例子：选取了常用的一组近红外量测玉米的光谱数据，光谱测量采用mp5仪器，该量测数据x包含80个玉米样本，玉米的淀粉含量作为响应变量y，光谱波长区间为1100～2498 nm，间隔为2 nm，总获得700个量测波长（该数据可从http：//www.eigenvector.com/data/Corn/index.html免费下载）。PLS作为校正模型的方法，蒙特卡洛采样次数N=10000，每次采样，80%样本作为训练集，剩下的20%样本作为独立测试集，PLS潜变量个数由10折交互检验选取为9，采用MCS方法对该数据的奇异样本诊断结果如图3所示，MCS判断出了三类样本分别为正常样本（图3a），X方向奇异样本（图3b）和Y方向奇异样本（图3c和d）。图3A显示了对应的a， b， c 三类样本的预测误差分布图，可以看出正常样本A，预测误差分布在原点附近，均值接近0，分布高而窄，说明其有很小的不确定性。对于X方向的奇异样本，由于其远离数据主体，用不同的样本得到的不同的模型将会产生一个很宽的预测误差分布，标准差较大。而对于Y方向的奇异样本，预测误差分布的均值远离原点和标准差也较大。因此，这些结果都表明，仅利用一次模型得到的一次预测误差诊断奇异样本是不充分，采用预测误差分布来诊断奇异样本才更加可靠和稳健，这是采用模型集群分析获得多个模型的重要原因。

图3 A： 根据预测误差的均值与标准差画出的奇异值诊断图， 三类样本分别为正常样本（a），X方向奇异样本（b）和Y方向奇异样本（c和d）； B： 三类样本（a，b和c）的预测误差分布图

Fig.3 （A） The diagnostic plot for outlier detection based on the mean and STD value of prediction errors. Three representative samples are a normal sample （a）， an X-outlier （b）， and a Y-outlier （c and d ）； （B） The distributions of prediction errors of these a， b and c samples

4.2 变量选择

现代高通量分析仪器的成千上万个分析通道可提供丰富的测量数据，但常遇到到“样本少，变量多”问题[24，25]。而变量选择无疑是解决此类问题的有效方法[26]。Yun等[27]也证明了复杂分析体系中变量选择的重要性与必要性。选择变量有3个目的：（1）提高预测能力；（2）降低数据维数并选择更有效的变量；（3）增强模型的可解释性[28]。然而，变量选择是一个NP问题，随着变量个数的增加，变量空间成指数增大，找到一个最佳变量组合非常具有挑战性。基于模型集群分析的框架思路，新近提出了众多变量选择方法，这里简单介绍一个代表性方法并举出相关应用例子。基于变量组合的变量重要性分析（VIAVC）[29]是基于模型集群分析思路对每个变量进行重要性分析的方法。具体步骤如下：（1）采用二进制采样从原始数据总样本中产生N个变量组合，每个变量组合含有一组随机变量；（2）每个变量组合建立一个子模型并计算其交互检验预测误差或准确率，即可获得交互检验预测误差或准确率的分布；（3）对每个变量，观察其存在或不存在某个固定变量组合时前后的差别，因有N个变量组合，每个变量都有存在与不存在某个固定变量组合的分布，采用统计检验对对其进行评价，得出的p值即可作为评价变量重要性的标准；（4）只保留p<0.05的变量，重复上述步骤1～3，直至无p>0.05的变量。endprint

选取一组代谢组学数据[30]作为此方法的应用例子，该数据两类样本采自中南大学湘雅医学院的16例正常儿童血浆样本和13例超重儿童的血浆样本。通过岛津GCMS-QP2010气相色谱与质谱联用仪分析并采用NIST质谱库检索定性定量分析了30个代谢产物。VIAVC目的是找出重要的代谢物，这些代谢物用于建模时能够达到变量选择的3个目的，即（1）提高两类样本的预测准确率；（2）选择少并有效的变量来建模；（3）变量的可解释性。根据VIAVC原理，以受试者工作特征曲线 （Receiver operating haracteristic curve， ROC曲线）下面的面积（Area under roc curve，AUC）作为模型评价指标[31， 32] ，结合统计t检验，挖掘出4类变量（图4），分别为强有信息变量、弱有信息变量、无信息变量和干扰变量。经过3次迭代后，VIAVC最终保留了13个有信息变量，根据统计检验对两个分布计算的p值来排序这13个变量，最后再利用10折双层交互检验按照排序向前选择，找出最佳的变量组合，前3个变量。这3个代谢物分别为β-羟基丁酸、甘油酸和棕榈酸，他们的交互检验预测准确率为86.21%，与全部变量的交互检验预测准确率65.52%相比，选择变量大大提高了预测能力，所选择的3个代谢物也被验证与肥胖疾病有关[33～35]。

图4 4类变量分布图，a为强有信息变量，存在该变量时，交互检验AUC值（AUCCV）显著性提高，t检验p0.05；b为弱有信息变量，存在该变量时， AUCCV稍微有提高但不显著，t检验p>0.05；c为无有信息变量，存在该变量时，AUCCV稍有降低但不显著，t检验p>0.05；d为干扰变量，存在该变量时， AUCCV显著性降低，t检验p<0.05。

Fig.4 Four kinds of variable， a is the strongly informative variable， when inclusion of this variable， area under roc curve （AUC） value of cross validation （AUCCV） has improved significantly， and p value of t test is much less than 0.05； b is the weakly informative variable， when inclusion of this variable， AUCCV has improved but not significantly， and p value of t test is more than 0.05； c is the uninformative variable， when inclusion of this variable， AUCCV has decreased a little， and p value of t test is more than 0.05； d is the interfering variable， when the inclusion of this variable， AUCCV has decreased significantly， and p value of t test is much less than 0.05

除了以上方法，近年来有很多基于模型集群分析思路开发的变量选择新方法，Monte Carlo based uninformative variable elimination （MC-UVE）[36]， Competitive adaptive reweighted sampling （CARS）[37，38]，Margin influence analysis （MIA）[39]，Iteratively retaining informative variables （IRIV）[40]，Random frog[41，42]，Variable combination population analysis（VCPA）[17]，Variable iterative space shrinkage approach （VISSA）[15，16]，Modified mutual information-based feature selection algorithm （MMIFS）[43]，Randomization test（RT）[44]，Variable complementary network（VCN）[45]， Subwindow permutation analysis （SPA）[4，46]。在图5中，每种方法的采样技术、采样空间、参数输出、统计分析均通过连接线画出。如MC-UVE方法，首先采用“蒙特卡洛采样”从“样本空间”里产生子数据集，对每个变量的“回归系数”进行“均值方差比”统计分析来评价变量重要性。用于光谱波段选择及QSAR描述符选择的方法有：MC-UVE，CARS，IRIV，VISSA，VCPA，RT，Random Frog。用于代谢组学的生物标记物选择的方法有VIAVC，VISSA，SPA，MMIFS，CARS，Random frog，VCN。用于基因组学及蛋白组学特征选择的方法有VIAVC，Random frog，MIA。

4.3 模型参数与评价

模型参数与评价是化学建模研究的一个基础问题[47]，任何模型的研究都离不开模型评价。目前，有很多模型评价信息标准，如AIC，BIC，DIC和Cp统计量等[48]。交互检验是比较常用的模型评价方法，只得到一个值用来评价，如交互检验预测误差。然而，仅用预测误差评价模型是不足的[49～51]。Deng等[52]提出了一种基于模型集群分析并结合模型预测能力与模型稳定性评价模型的方法。该方法应用于PLS回归模型，以确定PLS潜变量个数这个参数。对于PLS回归模型，模型稳定性可以根据回归系数的方差判断。具体步骤如下：（1）采用蒙特卡洛采样从原始数据总样本中选取80%的样本作为训练样本，剩下20%的样本作为独立测试集样本。这个过程重复N次，将去获取N个子训练集和与之对应的N个子测试集；（2）每个子训练集建立模型并对相应的测试集样本进行预测。同时，记录每个子模型的PLS回归系数；（3）根据模型预测误差来获得模型预测能力，同时根据PLS回归系数来获得模型稳定性；（4）根据不同的PLS潜变量个数，重复步骤1～3，选择同时具有好的预测能力及稳定性的PLS模型。endprint

在此，选取常用的一组近红外光谱测量角叉胶的数据[53]，该量测数据包含128个样本，每条近红外光谱包含701个数据点。PLS作为校正模型的方法。留一交互检验（LOOCV），五折交互检验（5-fold CV）和蒙特卡洛交互检验（MCCV）的结果显示，最优的潜变量数很难确定，因为不同潜变量数的模型有非常接近的交互检验均方根误差（图6A）。然而，从模型稳定性的角度我们可以发现潜变量为6的模型稳定性明显高于其它潜变量数的模型，如图6B所示。模型的稳定性在这里用回归系数之间的欧式距离衡量。潜变量数为6的模型回归系数之间的欧式距离的值明显小于潜变量数为1和20的模型，欧式距离的分布也更集中。值得注意的是，潜变量数为20的模型比潜变量数为6的模型预测误差稍小。但是，结合模型稳定性，选择的最优潜变量数是6。

图6 （A）不同方法确定潜变量数（nLV）的结果，蓝色代表留一法交互检验（LOOCV），紫红色代表5折交互检验（5-fold CV），浅蓝色代表蒙特卡洛交互检验（MCCV），红色代表基于模型集群分析的方法（MPA-based）； （B）不同模型复杂度的回归系数之间的欧氏距离

Fig.6 （A）Determination of the number of latent variables by different methods， blue represents leave one out cross validation， purplish red represents five-fold cross validation， light blue represents Monte Carlo cross validation and red represents MPA-based. （B） Euclidean distance between PLS regression coefficient on different model complexities （The number of latent variable， nLV=1， 6 and 20）

4.4 稳健与模型应用域

奇异样本诊断往往应用于建立模型前去除奇异样本，而模型应用域则是在模型建立后在应用上需要定义的，是化学建模中至关重要的一步，决定着建立好的模型的应用范围。给定一个建立好的模型，对于需要预测的外来新样本，其与模型应用域的关系存在3种情况：（1）新样本在模型应用域内，即所建模型考虑到了该样本的信息，可被很好的预测，即预测误差小；（2）新样本处在应用域边缘，即模型只考虑了该样本的部分信息，其可被预测但精度不高，预测误差较大；（3）新样本完全处在模型应用域外，即所建模型完全没有考虑了该样本的任何信息，因此该样本无法被准确预测，预测误差极大。而目前有很多模型应用域的方法[54]，基于范围和几何原理的方法[55]，基于主成份分析的方法[56]，基于凸包原理（Convex Hulls）的方法[57]，基于化学相似性的方法[58]，基于概率密度的方法[59]和基于模型集群分析的方法[60，61]。

基于模型集群分析的方法，通过在样本空间或者变量空间随机得到多个子模型，并且对子模型的预测方差进行统计分析，从而确定模型的应用域[60]，其步骤如下：（1）采用蒙特卡洛采样从原始数据总样本中选取一定比列的样本作为训练样本，如r=80%，剩下20%的样本作为独立测试集样本。这个过程重复N次，将去获取N个子训练集和与之对应的N个子测试集；（2）每个子训练集建立模型并对相应的测试集样本进行预测，即可得到N个测试结果；（3）统计每个测试样本的预测误差的分布，计算每个样本预测误差的标准差。在此选取Hou等[62]报道的一组QSAR数据进行分析。该数据包含1290个化合物 （样本），324个分子描述符 （变量）。首先，将样本划分为训练集（411个），测试集1（410个）和测试集2 （466个）。训练集和测试集1的化合物只包含C， H， O和N元素，而测试集2的化合物除了含有C， H， O和N元素外，还含有其它元素。 用训练集进行建模，可以预计测试集1的样本在模型应用域里面，而测试集2的样本则在模型应用域之外。结果如图7a所示，测试集2的样本（紫红色）预测误差的标准差明显大于训练集（蓝色）和

图7 应用域描述图：a，预测误差值与其标准差值之间的关系，蓝色圆圈代表训练集，绿色菱形代表测试集1，紫红色星号代表测试集2； b，两个典型的样本（a图的A和B）的预测误差分布图，A样本在模型应用域里，B样本在模型应用域外

Fig.7 Description of applicability domain： （a） The relationship between the standard deviation values and the values of prediction error， green rhombus denote training data； blue circles denote test data 1； and purplish red star denote test data 2； （b） The distrubution of prediciton errors for two selected sampels marked in the left panel. Sample A is inside the applicability domain and sample B is outside the applicability domain测试集1的样本（绿色），说明该方法能够很好地划分模型的应用域。图7b呈现的分别是测试集1和测试集2中的两个典型样本A和B的预测误差的分布。样本A为模型应用域内的样本，而样本B为模型应用域外的样本。样本B的预测误差明显大于样本A，同时样本B的预测的变化范围也远大于样本A。endprint

5 结论与展望

值得指出的是，模型集群分析的主要思路是从多个视点看待化学建模，并通过多次建模以尽量逼近建模基空间；同时，通过多个子模型比较，以避免模型的过拟合或其他建模陷阱，为化学建模提供了新思路。另一方面，模型集群分析实际是提供了一种一般性研究框架，可以从3个基本要素4个空间里选择改变某一点或几点作为切入口，开发一种应用于化学建模的新算法。也就是，在样本空间、变量空间、参数空间或模型空间的任何一个空间或多个空间，改变随机采样方法，改变建立子模型的方法，以及用不同统计方法分析不同的感兴趣的输出参数。同时，模型集群分析为化学建模在奇异值诊断，变量选择，模型参数与评价以及模型应用域的算法设计上提供了一种新的思维方式，为解决复杂多组分体系的高通量分析提供了新手段。在这里，我们讨论的基于模型集群分析的方法及应用是有限的，实际上，模型集群分析的泛化性很强，可以延伸到其它领域，如基因组学、蛋白组学等组学分析，以及生物信息学领域。未来可基于模型集群分析从基因和蛋白组学等大数据挖掘方向开发化学建模新算法，解决当今大数据时代急需的计算应用，但开发化学建模新算法同时应注重算法的应用性，应以能解决实际问题为出发点。

References

1 LIANG Yi-Zeng， XU Qing-Song. Instrumental Analysis of Complex Systems-White， Grey and Black Analytical Systems and Their Multivariate Methods. Beijing： Chemical Industry Press， 2013： 1-18

梁逸曾， 许青松. 复杂体系仪器分析─白、灰、黑分析体系及其化学计量学算法. 北京： 化学工业出版社， 2013： 1-18

2 Cawley G C， Talbot N L C. Bioinformatics， 2006， 22（19）： 2348-2355

3 Chen T， Martin E. Anal. Chim. Acta.， 2009， 631（1）： 13-21

4 Wang Q， Li H D， Xu Q S， Liang Y Z. Analyst， 2011， 136（7）： 1456-1463

5 Yeung K Y， Bumgarner R E， Raftery A E. Bioinformatics， 2005， 21（10）： 2394-2402

6 Candes E， Tao T. Ann. Stat.， 2007： 2313-2351

7 Johnstone I M， Titterington D M. Philos. Trans. A. Math. Phys. Eng. Sci.， 2009， 367（1906）： 4237-4253

8 Zou H， Hastie T. J. Roy. Stat. Soc. B.， 2005， 67（2）： 301-320

9 Li H D， Liang Y Z， Xu Q S， Cao D S. J. Chemometr， 2010， 24： 418-423

10 Li H D， Liang Y Z， Long X X， Yun Y H， Xu Q S. Chemometr. Intell. Lab.， 2013， 122： 23-30

11 Li H D， Liang Y Z， Cao D S， Xu Q S. TRAC-Trend. Anal. Chem.， 2012， 38： 154-162

12 Efron B， Efron B. The jackknife， the bootstrap and other resampling plans. SIAM， 1982： 1-92

13 Miller R G. Biometrika， 1974， 61（1）： 1-15

14 Efron B， Tibshirani R J. An Introduction to the Bootstrap.， Boca Raton： CRC Press， 1994： 1-404

15 Deng B C， Yun Y H， Liang Y Z， Yi L Z. Analyst， 2014， 139（19）： 4836-4845

16 Deng B C， Yun Y H， Ma P， Lin C C， Ren D B， Liang Y Z. Analyst， 2015， 140（6）： 1876-1885

17 Yun Y H， Wang W T， Deng B C， Lai G B， Liu X B， Ren D B， Liang Y Z， Fan W， Xu Q S. Anal. Chim. Acta.， 2015， 862： 14-23

18 Yun Y H， Wang W T， Tan M L， Liang Y Z， Li H D， Cao D S， Lu H M， Xu Q S. Anal. Chim. Acta.， 2014， 807： 36-43

19 Zhang H Y， Wang H Y， Dai Z J， Chen M S， Yuan Z M. BMC Bioinformatics.， 2012， 13（1）： 298-317

20 Edgington E， Onghena P. Randomization tests. Boca Raton： CRC Press， 2007： 1-998endprint

21 Mann H B， Whitney D R. Ann. Math. Statist.， 1947， 18（1）： 50-60

22 Egan W J， Morgan S L. Anal. Chem.， 1998， 70（11）： 2372-2379

23 Cao D S， Liang Y Z， Xu Q S， Li H D， Chen X. J. Comput. Chem.， 2010， 31（3）： 592-602

24 Fan J， Li R： Statistical Challenges with High Dimensionality： Feature Selection in Knowledge Discovery. In： Proceedings of the Madrid International Congress of Mathematicians： 2006； Madrid

25 Cai T T， Shen X. High-Dimensional Data Analysis. Beijing： Higher Education Press， 2010： 119-145

26 Spiegelman C H， McShane M J， Goetz M J， Motamedi M， Yue Q L， Coté G L. Anal. Chem.， 1998， 70（1）： 35-44

27 Yun Y H， Liang Y Z， Xie G X， Li H D， Cao D S， Xu Q S. Analyst， 2013， 138（21）： 6412-6421

28 Guyon I， Elisseeff A. J. Mach. Learn. Res.， 2003， 3： 1157-1182

29 Yun Y H， Liang F， Deng B C， Lai G B， Vicente Gonalves C， Lu H M， Yan J， Huang X， Yi L Z， Liang Y Z. Metabolomics.， 2015， doi：10.1007/s11306-015-0803-x

30 Zeng M M， Liang Y Z， Li H D， Wang M， Wang B， Chen X， Zhou N， Cao D S， Wu J. J. Pharmaceut. Biomed.， 2010， 52（2）： 265-272

31 Marrocco C， Duin R P W， Tortorella F. Pattern. Recogn.， 2008， 41（6）： 1961-1974

32 Zweig M H， Campbell G. Clin. Chem.， 1993， 39（4）： 561-577

33 Hulver M W， Berggren J R， Cortright R N， Dudek R W， Thompson R P， Pories W J， MacDonald K G， Cline G W， Shulman G I， Dohm G L et al. Am. J. Physiol. Endocrinol. Metab.， 2003， 284（4）： 741-747

34 Kien C L， Bunn J Y， Ugrasbul F. Am. J. Clin. Nutr.， 2005， 82（2）： 320-326

35 Proenza A M， Roca P， CrespíC， Llad I， Palou A. J. Nutr. Biochem.， 1998， 9（12）： 697-704

36 Cai W S， Li Y K， Shao X G. Chemometr. Intell. Lab.， 2008， 90（2）： 188-194

37 Li H D， Liang Y Z， Xu Q S， Cao D S. Anal. Chim. Acta.， 2009， 648（1）： 77-84

38 Zheng K Y， Li Q Q， Wang J J， Geng J P， Cao P， Sui T， Wang X， Du Y P. Chemometr. Intell. Lab.， 2012， 112： 48-54

39 Li H D， Liang Y Z， Xu Q S， Cao D S， Tan B B， Deng B C， Lin C C. Ieee. Acm. T. Comput. Bi.， 2011， 8（6）： 1633-1641

40 Deng B C， Yun Y H， Liang Y Z， Yi L Z. Analyst.， 2014， 139（19）： 4836-4845

41 Li H D， Xu Q S， Liang Y Z. Anal. Chim. Acta.， 2012， 740： 20-26

42 Yun Y H， Li H D， E. Wood L R， Fan W， Wang J J， Cao D S， Xu Q S， Liang Y Z. Spectrochim. Acta. A.， 2013， 111： 31-36

43 Long X X， Li H D， Fan W， Xu Q S， Liang Y Z. Chemometr. Intell. Lab.， 2013， 121： 75-81

44 Xu H， Liu Z C， Cai W S， Shao X G. Chemometr. Intell. Lab.， 2009， 97（2）： 189-193endprint

45 Li H D， Xu Q S， Zhang W， Liang Y Z. Metabolomics.， 2012， 8（6）： 1218-1226

46 Li H D， Zeng M M， Tan B B， Liang Y Z， Xu Q S， Cao D S. Metabolomics.， 2010， 6（3）： 353-361

47 Gramatica P. Qsar. Comb. Sci.， 2007， 26（5）： 694-701

48 Akaike H. IEEE. T. Automat. Contr.， 1974， 19（6）： 716-723

49 Breiman L. Mach. Learn.， 2001， 45（1）： 5-32

50 Varma S， Simon R. BMC Bioinformatics.， 2006， 7（1）： 91-98

51 Hawkins D M， Basak S C， Mills D. J. Chem. Inf. Comp. Sci.， 2003， 43（2）： 579-586

52 Deng B C， Yun Y H， Liang Y Z， Cao D S， Xu Q S， Yi L Z， Huang X. Anal. Chim. Acta.， 2015， 880： 32-41

53 Dyrby M， Petersen R V， Larsen J， Rudolf B， Nrgaard L， Engelsen S B. Carbohyd. Polym.， 2004， 57（3）： 337-348

54 Dimitrov S， Dimitrova G， Pavlov T， Dimitrova N， Patlewicz G， Niemela J， Mekenyan O. J. Chem. Inf. Model.， 2005， 45（4）： 839-849

55 Sahigara F， Mansouri K， Ballabio D， Mauri A， Consonni V， Todeschini R. Molecules.， 2012， 17（5）： 4791-4810

56 Wold S， Esbensen K， Geladi P. Chemometr. Intell. Lab.， 1987， 2（1-3）： 37-52

57 Preparata F， Shamos M： Convex Hulls： Basic Algorithms. In： Computational Geometry. Springer New York； 1985： 95-149

58 Netzeva T I， Worth A P， Aldenberg T， Benigni R， Cronin M T， Gramatica P， Jaworska J S， Kahn S， Klopman G， Marchant C A. ATLA. 2005， 33： 155-173

59 Jaworska J， Nikolova-Jeliazkova N， Aldenberg T. ATLA-NOTTINGHAM-. 2005， 33（5）： 445-459

60 Kaneko H， Funatsu K. J. Chem. Inf. Model.， 2014， 54（9）： 2469-2482

61 Yan J， Zhu W W， Kong B， Lu H B， Yun Y H， Huang J H， Liang Y Z. Mol. Inform.， 2014， 33（8）： 503-513

62 Hou T， Xia K， Zhang W， Xu X. J. Chem. Inf. Comp. Sci.， 2004， 44（1）： 266-275endprint