高载能负荷峰谷分时电价优化研究

汪宁渤

高载能负荷峰谷分时电价优化研究

汪宁渤

汪宁渤1李 津1薛婷婷2刘彩霞2

1.甘肃省电力公司风电技术中心；2.兰州理工大学电气工程与信息工程学院

引言

目前需求侧管理（DSM）在国内外得到了广泛的应用，它通过价格的讯息，让消费电力的机构采用了合理的用电方式以及用电结构。DSM中有效的措施之一就是峰谷分时电价（Time- of- use），是供电部门根据电网的负荷特性确定高峰段、低谷段、平时段的，根据不同的用电时段来规定不同的电价，即用电高峰期价格上升，用电低谷期价格降低，在经济方面可以激励电力消费者对用电方式有所改变，从而缓解了高峰期的用电紧张状况，寻找低谷期的用电，并实施峰谷分时电价的措施来达到削峰填谷的目的。首先需要确定的负荷曲线，才可以进行准确的电价计算，同时可忽略定价后负荷的变动。实际上，负荷是随电价的变化而变化的，即负荷被电价控制着。因此，电力系统的运行与预期运行最优方式有所差异。根据上述对电价的理解，本文提出了基于DSM分时电价的数学模型，得到了合理的电价算法。

高载能负荷电价数学模型

文中的电价数学模型是根据下面的假设提出的：

（1）日用电量在实施峰谷分时电价前后的变化可忽略；

（2）从时间轴上看，某个时段转移到另个时段的电量是平均分配的；

（3）只考虑价格对需求的影响，其他因素暂不考虑。

峰谷时段划分

峰谷时段的划分是为了激励电力消费者合理的调整用电方式，来确定合理的电价，达到削峰填谷的目的，使负荷曲线形状合理的变化。文中将1d的24h进行峰谷时段划分，假设共有n种分法，每种记为则总的峰谷时段划分集合为将一天24h划分为3类时段即：

高载能负荷对峰谷电价的反应

1）峰值时段的反应

w1j：实施前j 负荷的高峰用电量；

w1j'：实施后j 负荷的高峰用电量；

2）平值时段的反应

平值反应度（λ2j）：实施分时措施后，负荷j从平值时段向低谷段移动的用电量和节约电量和与平值用电量的比值：

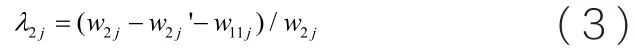
w11j：负荷j 从高峰段移动到平值段的耗电量。

w2j'：实施后j负荷的平值段耗电量。

3）谷值时段的反应

由上文的假设（1）可得，实施分时措施后，负荷在低谷段的耗电量变为：

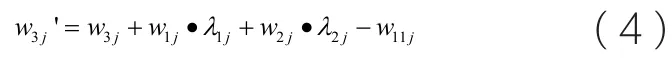
w3j'：实施措施后j 负荷的低谷段耗电量。

分时电价模型的建立

实行DSM的目的在于使供电部门和电力消费者双方都能受益，让供电部门降低降低生产成本，电力消费者减少支出，使DSM合理得到应用。

将实施分时措施前平均电价设为c0，全天总消耗电量为w0，则高载能企业支出M0为：

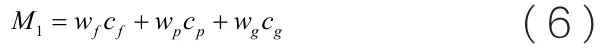
实行峰谷电价后，节省的电力投资为Mt。

1）供电方受益

对与供电方而言，采用分时电价可以使电力销售收入与未实施分时电价前相比没有降低，即：

2）用户端受益

用户实施峰谷电价的措施，该让实行峰谷电价后的电费支出M1不多于实行前的电费支出M0，即：

3）成本约束条件

∆c受边际成本的制约，即低谷段电价大于电力系统在谷值段的边际成本。

ce--电力系统在低谷段的边际成本。

4）优化目标

实行峰谷电价可以最大限度使峰荷降低，谷荷提高，峰谷差减小，来提高电力系统的负荷率，并使电力系统更稳定。

设在fi模型下实施峰谷电价后电力系统的日负荷曲线为Pfi，采取双目标规划来对日负荷曲线最大峰负荷和峰谷差进行优化，则目标函数为：

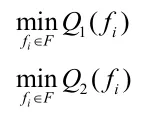
其中：

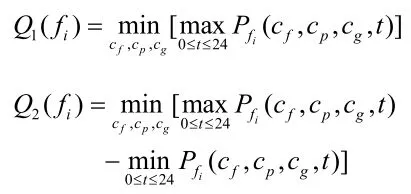
仿真计算

取2014年甘肃电网一组典型日负荷数据，实施峰谷分时电价前平均电价为系统在低谷段的边际成本为设实施峰谷电价后平时段的负荷电价与实行前的平均电价基本保持，实行前最大负荷、最小负荷是：

根据优化模型，对于不同的时段划分进行仿真，得到最优的峰谷时段划分如下。峰时段为：9：00～11：00， 17：00～21：00，共6h；谷时段为：23：00～次日7：00，共8h；平时段为其余时间，共10h。按照这种划分方法，高峰段电价为低谷段电价为最大负荷最小，峰谷差最小，且峰谷差相差不大。同时仿真出原来的时段划分（峰时段为7：00～11：00，17：00～21：00；谷时段为23：00～次日7：00；其余时间为平时段）如图1所示，通过比较得出最好的效果。

从图1可得出，负荷曲线通过采取最优时段和电价制定的方法有所改进，使负荷曲线变平滑，并且最大负荷有了明显下降，在一定程度降低了峰谷差，同时提高了电力系统的稳定运行以及经济水平。

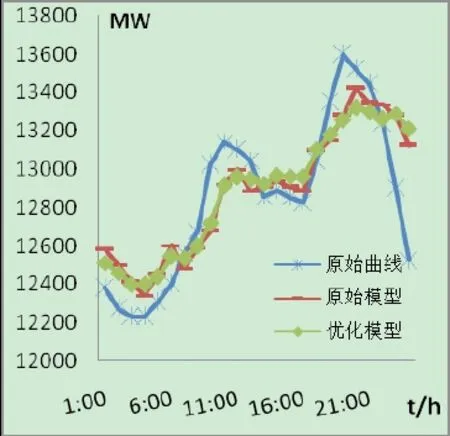
图1 日负荷曲线

结语

论文分析了对于供电企业和用户实施峰谷分时电价的意义，详细介绍峰谷平值段的划分方式，对高载能用户对峰谷分时电价的反应进行建模，并结合不同时段划分方法和电价制定方法给出了模型求解办法，得出①最优时段划分；②的分时电价定价方法。进行仿真，得到下列结论：

（1）峰谷平值段段的划分对峰谷分时电价的实施效果有重要的影响，合理的峰谷平值段划分，可以调整负荷曲线。

（2）与以前相比较，峰时段的时间从8h变为为6h。这符合高峰时段应尽量缩短的峰谷分时电价的原则。

10.3969/j.issn.1001-8972.2015.02.009