基于接触理论的螺栓联接接触面力学特性研究
章伊华,林丹益,YANG Guo-yu
(1.宁波大红鹰学院汽车CAE应用技术研究所,浙江宁波315175;2.EASi Engineering,Detroit 48201,Michigan,United States)
基于接触理论的螺栓联接接触面力学特性研究
章伊华1,林丹益1,YANG Guo-yu2
(1.宁波大红鹰学院汽车CAE应用技术研究所,浙江宁波315175;2.EASi Engineering,Detroit 48201,Michigan,United States)
运用多微凸体粗糙接触表面由弹性、弹塑性至塑性变形转化过程的连续光滑可导原理,论证了载荷作用下接触面接触强度及实际接触面之间的连续性和区域性。用混合单元法创建实际螺栓结构接触压力模型,求解出螺栓结构的实际接触面积与接触压应力分布。对比超声波实验数据,有限元分析(FEA)结果与超声波实验结果相吻合,验证了模型的正确性和有效性。通过系列模型,分析压应力沿螺栓方向的传递作用,证明螺栓联接结构接触应力在环形区域内分布的连续性,并探讨了改变预紧力和结构几何参数对螺栓联接接触强度、接触应力范围的影响规律。
固体力学;接触面力学;接触强度;螺栓联接;预紧力;接触压应力分布
0 引言
机械结构中,存在着大量由两个接触面组成的结合面。国际上对结合面接触力学的研究一直受到高度关注,作为工程应用的典型案例,螺栓联接结构由于其联接可靠、使用方便、结合面强度高等优点,被广泛应用于航空、汽车、船舶、发动机等现代装备技术领域。在受到预紧力和外载的双重作用下,螺栓联接结构内部应力状态及联接强度直接影响着结构乃至整机的安全与疲劳寿命,因此准确的预紧力设计[1]及螺栓结合面力学性能研究已成为工程界重点需要解决的课题。
围绕螺栓联接结构接触面的结合强度及力学特性,国内外学者已做了大量有益工作。Greenwood[2]、Fernlund[3]、Lardner[4]建议采用三维光弹性实验来测定被联接件间接触面的应力分布。随着有限元技术的发展和成熟[5],Gould等[6]以面载荷代替螺帽下的预紧力,用弹性理论和有限元方法分析了螺栓接触面积和压应力分布的非线性关系。Ziada等[7]利用有限元的方法建立螺栓结构3D模型,研究了螺栓结构尺寸对应力分布的影响。尤晋闽等[8]以分形接触理论建立结合面接触模型,提出了结合面实际接触面积仅占名义接触面积一小部分的结论。王世军等[9]采用表面形貌测量仪获取接触表面粗糙度并建立有限元弹塑性接触模型,初步探讨了载荷与接触面积之间的关系。赵永武等[10]在研究GW和CEB接触模型基础上通过弹塑性变形区间的接触方程及模型,在理论上探讨了弹塑性变形3个阶段接触面积随载荷增加的变化曲线。Marshall等[11]运用现代聚焦超声波测量技术通过对螺栓压紧接触面的超声扫描,来研究不同压紧力作用下接触面压力分布及对接触面积的影响。上述对螺栓结构接触面力学特性的研究在理论方法和实验测试方面都取得了许多有益的成绩。但这些研究仍主要停留在理论探讨和实验测试阶段,尚未实现理论与实验的有效对接和验证,与工程中接触面力学特性的实际研究及应用仍有很大差距。
本文综合运用弹塑性接触理论及分形几何理论,以实际结构和属性为出发点建立连续函数的接触单元、弹塑性单元等多元混合数值仿真模型,在已有优化螺栓最佳预紧力研究基础上,深入研究螺栓联接预紧力对接触面积的影响,分析不同结构不同预紧力下接触面的压应力分布状态,并对比超声波实验验证了仿真模型的有效性和可靠性。
1 弹塑性接触和分形几何理论
已有研究表明,接触面的多微凸体接触变形是涉及到分形几何理论和Hertz接触理论的、粗糙接触表面由弹性向弹塑性变形逐步转化的过程。GW模型作为传统的粗糙表面纯弹性接触模型,以分形理论的非平稳性、自相似性和多重尺度性表达了加工表面形貌特征下的接触问题,后来发展的MB模型和CEB模型同时考虑了弹性和塑性的影响,但它们都未能表达接触压力下从弹性变形到塑性变形的连续性问题。根据Hertz接触理论,当微凸体仅在弹性阶段发生变形时,实际接触面积可表示为

平均接触压力
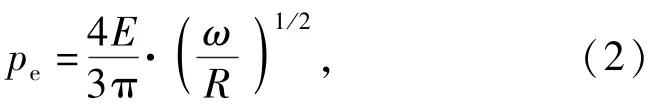
式中:ω为法向变形量;R为微凸体曲率半径。设屈服条件为

式中:k为平均接触压力系数;H为软材料的硬度。根据(2)式和(3)式,可得该材料的初始屈服临界法向变形[10]
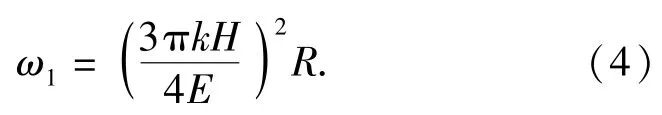
当微凸体发生完全塑性变形时,实际接触面积和临界法向变形量分别为

在这一阶段,其平均接触压力应该等于软材料的硬度

则当ω1≤ω<ω2时,接触面处于弹塑性接触变形阶段。由于弹性阶段和塑性阶段接触面积和接触压力的变化都是连续光滑,则弹塑性区间的接触面积A和平均接触压力pep的变化,在ω1~ω2之间时也是连续可导的。满足这些条件、处于弹塑性区间的A和pep,可以用以ω为自变量的两个多项式来表示,且该多项式应为单调递增的。为了获得这两个多项式,提出了(8)式形式的构造函数:
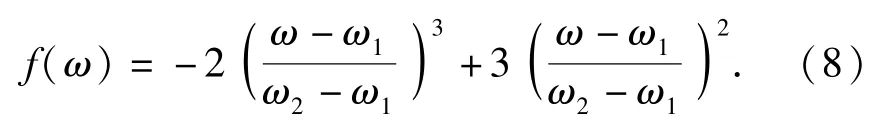
该函数在区间[ω1,ω2]范围内是单调递增的,且f(ω1)=0,f(ω2)=1,f′(ω1)=f′(ω2)=0.
设两个函数:弹性阶段y=Q(ω),0≤ω≤ω1;塑性阶段y=S(ω),ω2≤ω≤+∞.则在ω和ω2临界点连续光滑连接的函数必须满足条件:
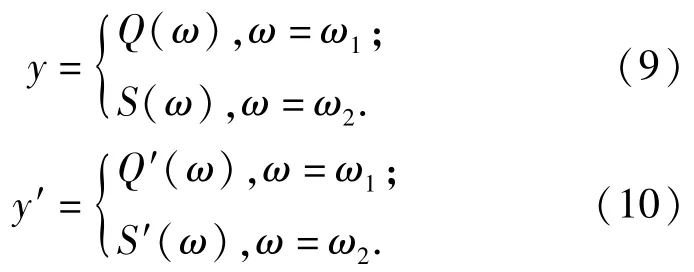
那么该函数可以用含上述构造函数的方程式表达为
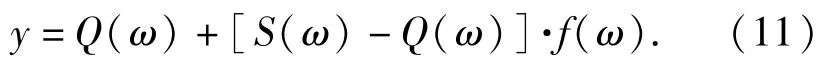
依据(11)式并参照图1,若Q(ω)=Ae,S(ω)= Ap,带入(11)式得
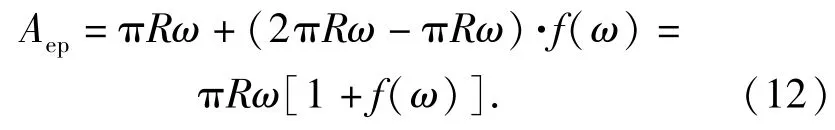
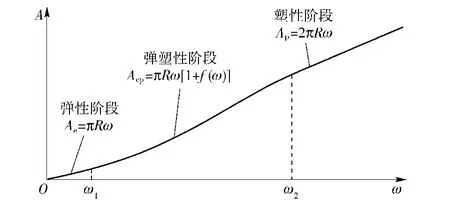
图1 3种变形阶段凸峰接触面积与法向变形量之间的关系Fig.1 Relationships between the hump contact area with the normal deformation in the three stages
同理,依据(11)式并参照图2,若Q(ω)=pe和S(ω)=pp,带入(11)式得
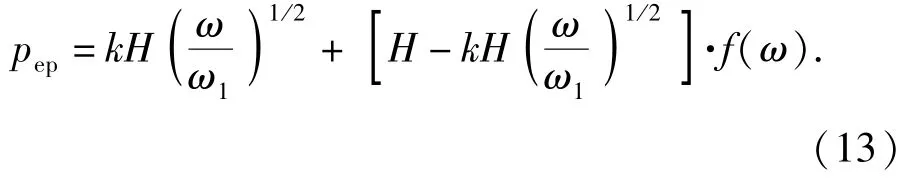
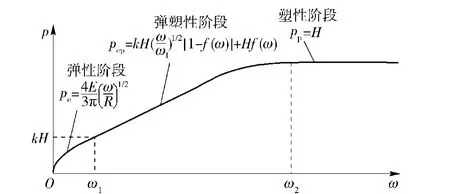
图2 3种变形阶段凸峰平均接触压力与法向变形量之间的关系Fig.2 Relationships between the hump average contact pressures with the normal deformation in the three stages
以微凸体变形3种阶段的实际接触面积和平均接触压力分布连续性为基础,可得两个粗糙表面的总接触面积和接触载荷公式。
设两接触面间距为d,则总实际接触面积
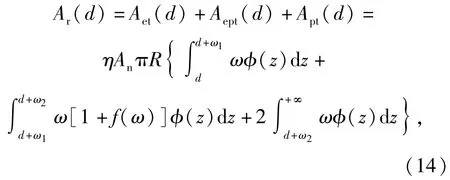
则总接触载荷
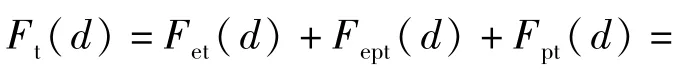
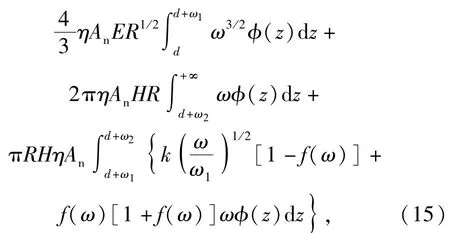
式中:An为名义接触面积;η为微凸体面积密度;φ(z)为微凸体高度分布的概率密度函数;Aet(d)为弹性接触面积;Aept(d)为弹塑性接触面积;Apt(d)为塑性接触面积;Fet(d)为弹性接触载荷;Fept(d)为弹塑性接触载荷;Fpt(d)为塑性接触载荷。
(14)式、(15)式有效反映了粗糙表面实际接触面载荷分布、变形强度关系及粗糙表面实际接触面3种变形阶段的连续性和区域性。
同时新的分形几何模型研究表明,分形粗糙表面在弹塑性变形过程中,表面分形维数会产生变化,一维分形可变为多重分形[12]。如MB模型中,假设粗糙表面与平面接触时,接触点面积分布密度函数n(a)遵循幂函数规[8],即
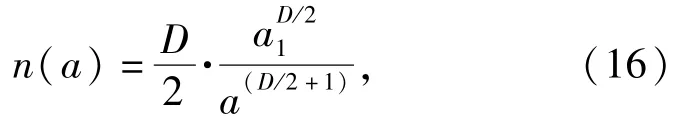
式中:a1为最大接触点面积;D为分形维数;a为接触点面积。总接触面积为
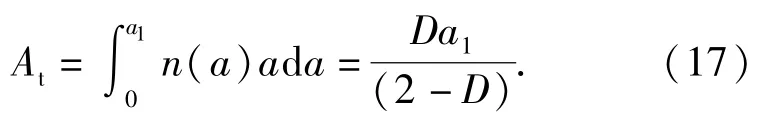
考虑弹塑性变形则实际接触面积增大,如(17)式所示。由此获得的实际接触总面积同(14)式中Ar具有同一性。本文通过对螺栓联接预紧力下接触面仿真获得的实际接触面积和载荷作用压应力分布曲线,亦证明了实际接触面积的连续性和区域性。
2 螺栓联接接触面力学特性研究
根据上述理论,假设实际工程中螺栓联接接触面力学特性遵从如下条件:
1)在接触区域内整体微凸体弹塑性接触变形具有连续性;
2)接触区域内整体微凸体接触概率[12]和粗糙表面峰高的概率均呈正态分布,且在载荷作用下趋于均衡;
3)在接触载荷Ft作用下,实际接触面积Aet的接触强度与Ft呈正向关系。由此,本文用混合单元法创建有限元数值模型分析螺栓联接接触面力学特性及压应力分布,并与实验数据对比,进一步论证实际接触面积分布的连续性和区域性。
2.1 模型建立
考察螺栓联接结构之间的接触受力关系,分别用M12通孔、M12盲孔螺栓结构建模如图3所示。在结合面,用接触面单元组成接触对,再以弹簧单元和其他有限单元建立混合单元模型。
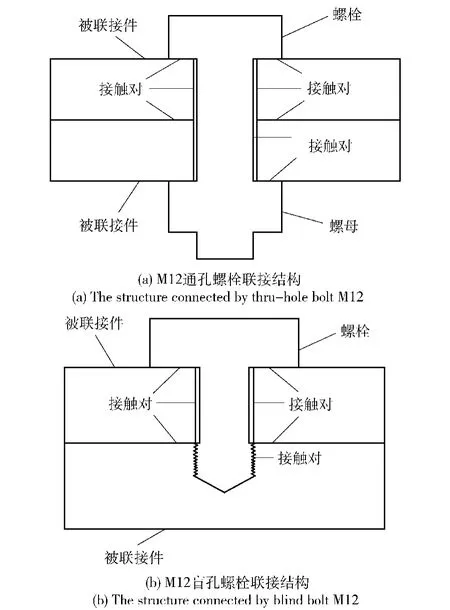
图3 模型结构图Fig.3 Structures of the models
螺栓、螺母材料:弹性模量取2.07×105MPa,泊松比取0.3,屈服极限取924 MPa,强度极限取1 130 MPa.
被联接件材料:弹性模量取2.07×105MPa,泊松比取0.3,屈服极限取355 MPa,强度极限取600 MPa.
对每组模型先后施加30 N·m、40 N·m、50 N·m、60 N·m扭矩力。考虑到螺纹结构安全可靠性要求,在分析中已引用最佳预紧力设计[1],在板与板及螺栓与板之间的各个接触面间建立摩擦接触。根据螺母、螺帽与被联接件的材料属性、表面粗糙度及润滑方式不同,摩擦系数取值范围为0.2~0.4.
2.2 预紧力施加及分步求解
模型在ABAQUS环境下求解,螺栓预紧力计算式:

式中:T为螺栓承受扭矩;K为拧紧力矩系数;F0为预紧力;db为螺栓直径。模型以F0/n分步施加预紧力并输出相应的结果数据。
2.3 分析与验证
从Hertz接触理论发展到GW模型、CEB模型及之后以塑性指数Ψ为表征的其他分形几何模型,接触问题的研究更多徘徊在计算理论范畴内。由于实体结构在外力作用下的接触压力及其分布,具有复杂的不同状态和非线性特性,因此上述理论模型均未能对具体接触面压应力做出准确计算和描述。同时,国际上相关测试实验研究有了新的推进和发展:文献[4,13]通过各种传统的测试方法研究螺栓接触应力分布,认为接触应力主要集中在围绕螺孔的圆周区域内呈非线性分布;文献[11]运用现代聚焦超声波技术研究盲孔螺栓结构接触应力,发现在预紧力作用下被压件接触面接近孔边的接触压力最大,远离孔边接触压应力逐渐降低,到一定距离应力值为0.
如图4所示扭矩为30 N·m、40 N·m、50 N·m、60 N·m时聚焦超声波测量出的接触压力。在夹紧界面,其沿螺栓孔呈圆形区域分布,其中亮色区域为高应力强度区。扭矩从30 N·m增大到60 N·m,亮色区域的亮度逐渐增强,但亮度区域面积并未扩大。为此本文创建了与实验盲孔螺栓结构完全相同的力学仿真模型,即几何参数、材料参数和预紧力完全一致,通过仿真计算获得的接触压应力云图如图5所示。
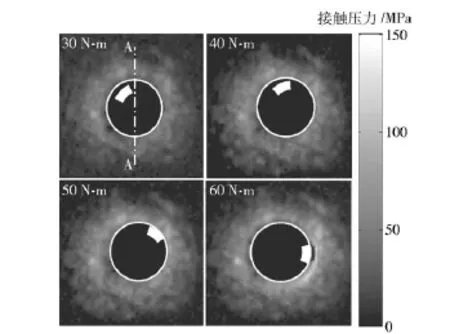
图4 M12盲孔螺栓超声波实验接触压应力图Fig.4 The contact pressure of blind bolt M12 in ultrasonic experiment
如图5(a)~图5(d)所示,分别显示了扭矩为60 N·m、50 N·m、40 N·m和30 N·m时夹紧接触面压应力分布,最大应力都位于靠近螺孔的(db/2+2)半径带内,不因预紧力的增大而改变,最大应力值分别为67.1 MPa、61.4 MPa、53.5 MPa和44.4 MPa.由于模型参数固定只改变预紧力大小,由图5(a)~图5(d)可见实际接触面积大小是一致的,应力强度、应变强度沿径向逐渐减小,预紧力的增加使得实际接触面内的应力沿径向呈递减式增加,实际接触面外的应力几乎没有变化,即加大外力只是增大实际接触面的应力强度、应变强度,不改变应力区域大小。这与图4超声波实验结果非常一致,也充分证明了实际接触面弹塑性3种变形阶段受力变形的连续性和区域性。
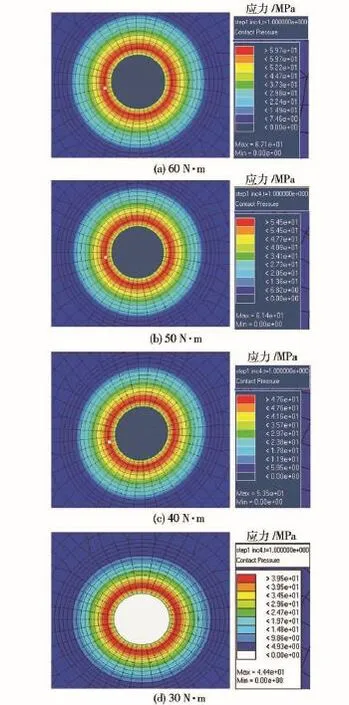
图5 M12盲孔螺栓仿真超声波接触压应力云图Fig.5 The contact pressure nephogram of blind bolt M12 simulating the ultrasonic model
对比图6和图7的仿真模型曲线和实验曲线可见,应力顶点及随后应力下降斜率呈较好的一致性。当接触面半径为18 mm时,二者应力值均进入零区域。在接触面半径接近21 mm处,实验曲线出现波动性,原因应为测试数据的零值误差或实验固定装置影响,故本模型计算结果能够较充分地验证了其与实验的一致性,从而证明了仿真模型的正确性、有效性和可靠性。在此基础上,用系列仿真模型进一步研究通孔螺栓联接结构接触面接触压应力及分布情况,如图8所示。压应力沿径向逐渐减小呈均匀下滑曲线,与超声波实验模型不同的是其最大接触面压应力位于靠近螺栓的螺孔壁上,加大外力或预紧力,同样不改变应力区域大小。
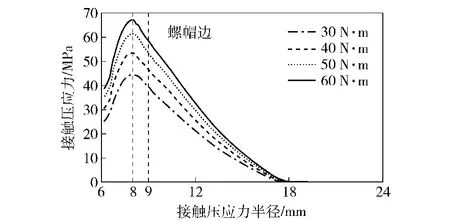
图6 超声波实验仿真模型接触压应力与作用半径曲线Fig.6 Curves of contact pressure and action radius of the ultrasonic experiment simulation with bolt model
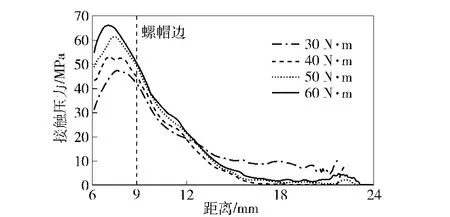
图7 超声波实验盲孔模型接触压应力与作用半径曲线Fig.7 Curves of contact pressure and action radius of the ultrasonic experiment with blind bolt model
2.4 影响接触应力作用的因素
由图6和图7接触压力作用半径曲线可见,超声波仿真模型和超声波实验结果都反映出作用力半径为18 mm时,压应力趋于0.说明微观上,在沿径向递减载荷作用下,微凸体接触由塑性应变逐渐趋于弹塑性和弱弹性,由此也证明了从弹性变形到塑性变形的连续性[12]。进一步研究发现,M12通孔仿真模型压应力半径为19 mm时,压应力趋于0,如图8所示,表明改变螺栓联接结构的几何关系实际接触面积会发生明显改变。本文用传统螺栓联接结构压力锥角来分析研究影响接触应力作用的因素,如图9所示。
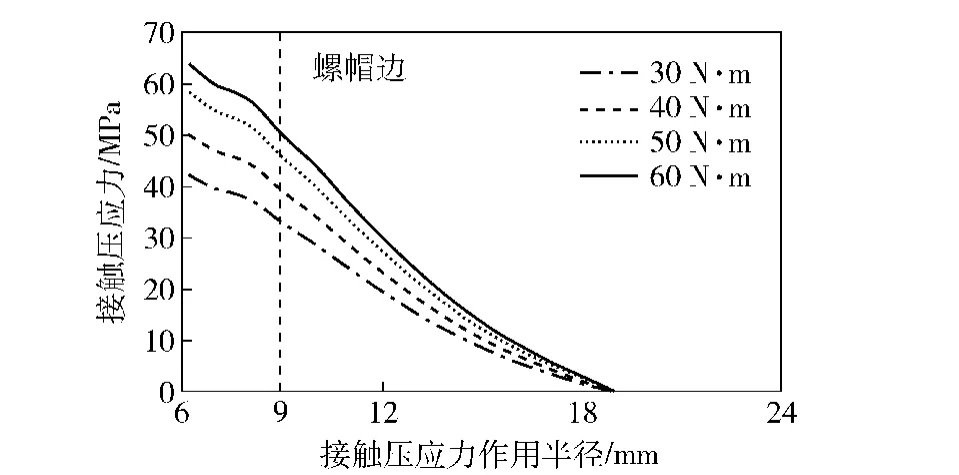
图8 通孔螺栓接触压应力与作用半径曲线Fig.8 Curves of contact pressure and action radius with thru-hole bolt model
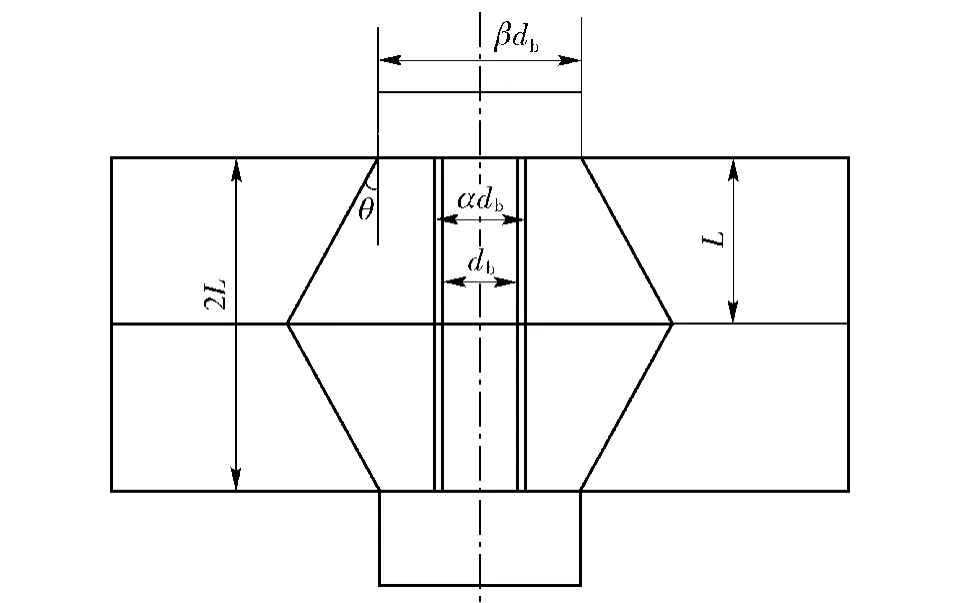
图9 压力锥角示意图Fig.9 Schematic diagram of pressure cone angle
工程上螺栓接触应力作用范围常用压力锥角θ来表示,且
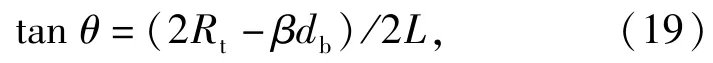
式中:Rt为接触应力作用半径(mm);β为螺母系数;db为螺栓直径(mm);L为被联接件厚度(mm)。
文献[6,11]采用理论分析及测试的方法给出了预紧力下螺栓结构不同的锥角θ取值,如表1所示。

表1 压力锥角的取值Tab.1 The values of pressure cone angle
由表1可见,锥角值差别很大,相互之间没有可对比和验证关系。本文在超声波实验模型基础上,通过调整系列参数的变化,根据螺帽接触面压应力和被连接板中间接触面压应力分布,研究预紧力、被联接件厚度及螺母大小等参数对锥角及接触应力半径的影响,发现锥角作用的影响规律,分析结果如图10~图12所示。
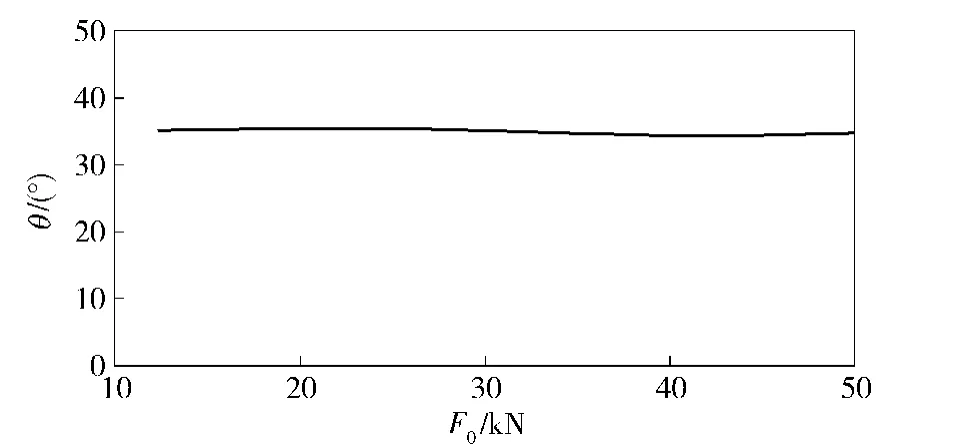
图10 锥角随预紧力的变化曲线Fig.10 Variation curve of cone angle with the pretightening force changing
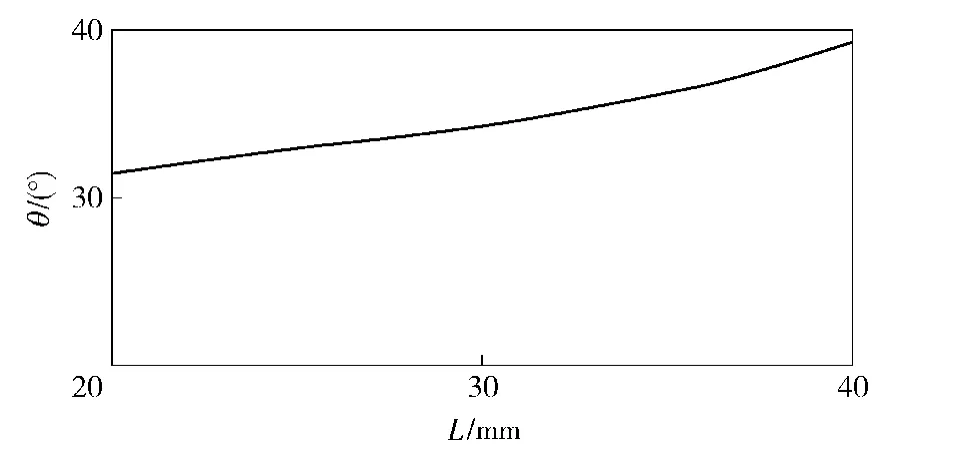
图11 锥角随被联接件厚度的变化曲线Fig.11 Variation curve of cone angle with the thickness of connecting plate changing
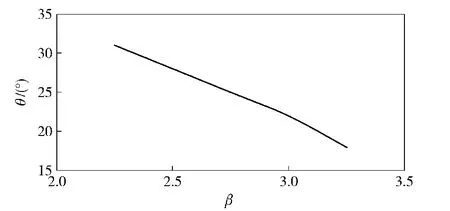
图12 锥角随螺母系数的变化曲线Fig.12 Variation curve of cone angle with the nut coefficient changing
图10表明锥角不随预紧力的增加而改变。由图11曲线可知,被联接件厚度越大,锥角越大,接触应力的作用区域越大。图12为锥角随螺母系数的变化曲线,可见锥角随螺母系数的增大而减小。
通过以上规律可知,在材料不变情况下,影响压力锥角的主要因素是螺栓结构的几何参数。接触表面粗糙度及表面微凸体影响不是改变螺栓结构压力锥角和接触面大小的主要因素,这一点具有重要工程意义。由此,可通过优化结构参数,得到最需的结构接触应力强度和有效接触应力面积,为重要工程的螺栓组合结构强度、刚度精确设计奠定了基础。
3 结论
本文基于Hertz接触理论和分形几何理论结合有限元分析技术,建立超声波实验仿真模型,分析了螺栓结构结合面接触面积和接触压力的分布规律及重要影响参数。结论如下:
2)超声波仿真模型的压应力强度随接触面半径变化曲线与超声波实验曲线具有较好的一致性,证明了仿真模型的有效性和可靠性。
3)结构改变会引起接触面积增大或减小,本文使用应力锥角,研究被联接件厚度、螺母系数及预紧力的作用影响,发现应力锥角是由螺栓结构的主要几何参数确定的,接触表面粗糙度、表面微凸体及预紧力不改变螺栓结构压力锥角和接触面大小。
(
)
[1]章伊华,侯培海,杨国玉.汽车螺纹联接件预紧力的优化设计[J].东北林业大学学报,2012,40(11):151-154. ZHANG Yi-hua,HOU Pei-hai,YANG Guo-yu.Optimized design of preload for tread connection of automobile[J].Journal of Northeast Forestry University,2012,40(11):151-154.(in Chinese)
[2]Greenwood A J.The elastic stresses produced in the mid-plane of a slab by pressures applied symmetrically at its surface[J].Mathematical Proceedings of the Cambridge Philosophical Society,1964(1):159-169.
[3]Femlund I.A method to calculate the pressure between bolted or riveted plates[J].Transactions of Charmers University of Technology,1961,245:13-51.
[4]Lardner T J.Stresses in a thick plate with axially symmetric loading[J].Journal of Applied Mechanics,1965,32(2):458-459.
[5]Yang G,Kabel J,van Rietbergen B,et al.The anisotropic Hooke's law for cancellous bone and wood[J].Journal of Elasticity,1999,53(2):125-146.
[6]Gould H H,Mikic B B.Areas of contact pressure distribution in bolted joints[J].Journal of Manufacturing Science and Engineering,1972,94(3):864-870.
[7]Ziada H H,Abd El Latyif A K.Loading conditions in bolted and riveted joints affected by plate thickness ratio[J].Journal of Mechanical Design,1980,102(4):93-100.
[8]尤晋闽,陈天宁.结合面法向动态参数的分形模型[J].西安交通大学学报,2009,43(9):91-94. YOU Jin-min,CHEN Tian-ning.Fractal model for normal dynamic parameters of joint surfaces[J].Journal of Xi'an Jiaotong University,2009,43(9):91-94.(in Chinese)
[9]王世军,赵金娟,张慧军,等.一种结合部法向刚度的预估方法[J].机械工程学报,2011,47(21):111-122. WANG Shi-jun,ZHAO Jin-juan,ZHANG Hui-jun,et al.A method of estimating normal stiffness of joint[J].Journal of Mechanical Engineering,2011,47(21):111-122.(in Chinese)
[10]赵永武,吕彦明,蒋建忠.新的粗糙表面弹塑性接触模型[J].机械工程学报,2007,43(3):95-101. ZHAO Yong-wu,LYU Yan-ming,JIANG Jian-zhong.New elasticplastic model for the contact of rough surfaces[J].Journal of Mechanical Engineering,2007,43(3):95-101.(in Chinese)
[11]Marshall M B,Lewis R,Dwyer-Joyce R S.Characterisation of contact pressure distribution in bolted joints[J].Strain,2006,42(1):31-43.
[12]杨红平,傅卫平,王雯,等.基于分形几何与接触力学理论的结合面法向接触刚度计算模型[J].机械工程学报,2013,49(1):102-107. YANG Hong-ping,FU Wei-ping,WANG Wen,et al.Calculation model of the normal contact stiffness of joints based on the fractal geometry and contact theory[J].Journal of Mechanical Engineering,2013,49(1):102-107.(in Chinese)
[13]Bickford J H.An introduction to the design and behavior of bolted joints[M].2nd ed.New York:Marcel Dekker Inc,1995.
Research on Mechanical Properties of the Contact Surfaces in Bolt Joints
ZHANG Yi-hua1,LIN Dan-yi1,YANG Guo-yu2
(1.Institute of Automobile CAE Applied Technology,Ningbo Dahongying University,Ningbo 315175,Zhejiang,China;2.EASi Engineering,Detroit 48201,Michigan,United States)
The continuous smooth derivable principle of micro-convex asperity contact surface within the elastic,elastic-plastic and plastic contact deformations is applied to demonstrate the contact strength and the continuity and regional disparity of the practical contact surfaces under loading.A bolt structure model is established using the mixed-element method,and the practical contact area and the contact stress distribution are solved.The predicted results from finite element analysis(FEA)are highly correlated with the ones obtained from ultrasonic physical tests.The correctness and validity of the model are verified. The transmission effect of stress along the bolt joint direction is investigated through series of models,the continuity of the contact stress of the bolt joint in the annular region is further proved,and the effect laws of changing the pretightening force and structure geometric parameters on the bolt joint contact strength and the range of contact stress are discussed.
solid mechanics;mechanics of contact surface;contact strength;bolt joint;pretightening force;contact stress distribution
O343;O344
A
1000-1093(2015)05-0946-07
10.3969/j.issn.1000-1093.2015.05.027
2013-12-19
浙江省自然科学基金项目(Y12E050062)
章伊华(1962—),男,副研究员。E-mail:576175872@qq.com

