大班数学学习困难儿童数学操作游戏干预的研究
李正清+周欣+田丽丽+康丹+徐晶晶


【摘要】本研究通过数学操作游戏对两名大班数学学习困难儿童关于“阿拉伯数字系统”的掌握以及“数的部分与整体关系”的理解进行干预。结果表明,干预后被试儿童这两方面的数学能力均有不同程度的提高。研究提示我们,完善“数字系统”——积累“数的分合”经验——发现“数的分合”规律——运用“数的分合”知识,可能是一条对早期数学学习困难儿童进行干预的有效途径。
【关键词】早期数学学习困难儿童;游戏干预;个案
【中图分类号】G610 【文献标识码】A 【文章编号】1004-4604(2015)10-0024-06
本研究中,早期数学学习困难(Mathematics learning difficulty)儿童是指智力发展正常,但数学发展水平显著低于同龄儿童的5~6岁儿童。早期数学学习困难的诊断并非是早早地给这些儿童贴上一个负面标签,而是要尽早查找其发展水平低下的原因,并提供有针对性的早期干预。〔1〕有研究表明,越早发现并尽早实施干预,就越能有效地帮助这些儿童。〔2〕
儿童早期的数学学习困难常常会出现负面累积效应,即随着时间的推移,其与同伴的发展水平差距越来越大,〔3〕到小学后再实施干预则往往为时已晚。〔4〕成长模型研究表明,学前班秋季和春季两个学期中数学得分均偏低的儿童,随后4~5年的数学学习发展速率和数学成绩也往往很低。数学学习困难儿童缓慢的成长速度与他们不理解数字集合、不能进行加法事实提取、不常使用分解策略有关。〔5〕我们前期的干预研究也发现,数学学习困难儿童对“数的部分与整体关系”存在一定的理解障碍,在干预过程中进步缓慢。并且,即使掌握了部分“数的分解与组合”知识,他们在加减运算中也不会主动运用这类知识,而仍然倾向于使用“数手指”等方法。〔6〕
本研究以数学操作游戏为手段,尝试通过完善数学学习困难儿童的数字系统及引导其通过自主操作,帮助其逐步建构起对“数的部分与整体关系”的理解,进而改善其数学能力。同时,探讨和总结对类似儿童进行个别训练与教育的有效方法。
一、研究设计
(一)被试的选取与鉴定
L,女,开始干预时月龄68个月,身体健康,无重大疾病史。父母均为大专文化水平,重视教育。家庭经济条件良好,与父母、祖父母一起生活。L喜欢参与绘画美工活动,性格开朗,社会性发展良好,乐于为集体服务。据带班老师描述,在幼儿园集体活动中,L反应速度一般,表现不甚积极,学习能力一般,数学能力较弱。
Y,女,开始干预时月龄73个月,身体健康,无重大疾病史。父母均为高中文化水平,家庭经济条件一般,家庭教养方式较为溺爱。Y性格开朗,语言发展较好,运动水平较高,社会交往能力较强,较受同伴欢迎。据带班老师描述,在幼儿园集体活动中,Y注意力时常不集中,学习欲望缺乏,数学能力较差。
L和Y是带班老师认定的“班上数学学习和发展最为缓慢”的儿童。研究者对其进行智商和数学能力测查。使用《韦氏学前儿童智力量表》(Wechsler preschool and primary scale of intelligence,以下简称WPPSI)对L和Y进行测查,发现两名儿童的智商均属于正常水平。使用儿童早期数学能力测验(Test of early mathematics ability,以下简称TEMA)对上海市普陀区三所幼儿园的大班儿童(N=339)进行数学能力测试,将数学能力分数排名在最后10%以内(临界值为104 分)的儿童确认为数学学习困难儿童。经测查和对比,研究者发现,L和Y的智力正常,但数学能力分数均低于104分,因此可视为数学学习困难儿童。在我们最终确定的全部数学学习困难儿童样本中(N=63;TEMA能力分M=95.97,SD=7.20),L的TEMA得分恰好等于数学学习困难儿童的筛选临界分数,也即高于数学学习困难组儿童的平均分数,可以说,其数学学习困难程度相对较轻;Y的TEMA得分比平均分数低了一个标准差,可以说,其数学学习困难程度相对较重。
(二)研究工具
由一位经过培训的学前教育专业研究生对L和Y进行干预前和干预后的测查。所有测查项目以一对一的形式在安静的幼儿园活动室里进行。干预前的测查在当年9月实施,干预后的测查在次年6月实施。
1.《早期儿童数学能力测验量表》(TEMA)
该量表是Ginsburg和Baroody修订的版本,是测查3~8岁儿童数学能力的标准化工具,也可以用来鉴别数学学习困难儿童。量表共72个项目,每个项目计1分。〔7〕课题组对量表进行了汉化,经检验,中文版量表具有良好的效度和信度。〔8〕
2.《中国-韦氏幼儿智力量表》(WPPSI)
该量表分言语和操作测验两部分,言语部分测验包括知识、分类、算数、词汇、理解、背数6个部分;操作部分测验分为填图、排列、积木、拼图、译码、迷津6个部分。每项测验均按照计分手册要求单独计分。语言量表、操作量表和全量表均分别求得智商分数。运用中国常模对测查结果进行分数转换。根据规定,在选取数学学习困难儿童时,排除智商分数低于80分的儿童。
(三)干预思路与计划
1.干预内容
有研究表明,数概念是儿童数学能力发展中的一个“中心概念”,它的发展不仅与儿童今后的数学学习直接相关,而且与儿童的思维能力发展有着密切联系。〔9〕儿童对数量集合的理解是其数概念发展的一项重要内容,要基于其对数词系统的掌握和对数的部分与整体关系的理解。儿童对数量集合的理解能够比一般认知学习能力更好地预测其数学学业成就,〔10〕因此,可以作为数学学习困难的筛查工具。〔11〕为此,本研究重点对被试儿童的数概念,主要包括阿拉伯数字系统、数的部分与整体关系进行干预。
数字系统是儿童早期数知识学习的一个最重要工具,对数字符号的掌握是儿童在表征水平上理解抽象数字系统要做到的第一步。研究表明,儿童的唱数水平与其数数技能和对数的理解有直接的关系,儿童掌握的数字链的长短可作为其数概念发展水平的重要标志之一。儿童对数字的掌握与其成熟、经验水平有关,儿童阿拉伯数字系统的习得在很大程度上受练习机会的影响。因此,如能在干预过程中提供大量的练习机会,数学学习困难儿童还是有可能进一步完善其数字系统的。〔12〕
数的部分与整体关系是指数的相加性组成原理,即任何自然数可以分成更小的数,也可以与其他的数组合成更大的数,在心理学中被称为部分-整体图式(Part-whole scheme)。它是儿童早期数学发展中一个极为重要的认知发展内容,也是儿童掌握数概念的一个重要内容,在加减运算中具有重要作用。这种对数的理解能够帮助儿童识别运算所涉及的数之间的部分与整体的关系,并运用这些关系去选择正确的运算方法,尤其是使儿童在不能直接用实物演示题目的情境中也有可能解题。〔13〕研究表明,儿童6岁时已基本理解这一关系,6岁半时则能够完全掌握。〔14〕因此,通过干预完全有可能让数学学习困难儿童理解这一关系。
2.干预策略
建构主义强调学与教过程中学习者的主动参与、自主学习和意义建构,认为情境、协作、会话和意义建构是学习环境的四大要素。因此,本研究通过数学操作游戏,为被试儿童创设有意义的问题情境,并通过与同伴、研究者的相互沟通、平等交流,构建一个学习共同体,以引导被试儿童进行相关探索、自我调节和意义建构。
3.干预计划
正确及熟练地数数是理解数的部分与整体关系的前提。因此,本研究先对被试儿童进行数数的干预,随后进行数的部分与整体关系的干预。研究从大班秋季学期(上学期)开始,每周干预两次(周一和周四上午),每次干预时长40分钟左右。上学期主要进行数数的干预,下学期主要进行数的部分与整体关系的干预。当被试儿童因故没来幼儿园时,当次干预计划向后顺延一次。上学期实施干预11次,下学期实施干预18次,共计29次,总时长约1160分钟。具体的干预计划见表1。
二、干预过程
(一)阿拉伯数字系统
儿童数字系统的学习和发展会经历两个阶段:初步认识数字阶段和完整掌握数字系统阶段。第二个阶段中,从不完整到完整掌握数字系统的水平又可分为五个层次:(1)“连串”水平,即是对一连串数字的单向整体记忆或背诵,与数数动作无关。(2)“不可断数链”水平,即已能分化辨认出单个数字但无法从一个任意数数起,数物体已成为可能。(3)“可断数链”水平,即已能视数字为既可分割又可相联的元素,可从任何一个数向前或向后数,说出相邻数。(4)“数链”水平,即数字已被视为可数单位,可用于计数运算或与某个特定数量的集合匹配。(5)“双向数链”水平,即可以熟练地从一个任意数顺数或倒数。〔18〕
研究发现,儿童所掌握的数字系统往往由三部分组成:(1)正确的数字链部分,如1~5。(2)固定的不正确部分,即儿童在多次数数中都重复相同但不正确的数字链,尤其是在13~17这一段,有些儿童可能会持续较长时间。(3)不固定也不正确的部分,即每次数到某段数字时都会产生既不同也不正确的数字链。〔19〕根据前期观察诊断,L和Y的数字系统掌握水平详见表2。
数数的干预主要通过“数字连线”和“数字卡片”游戏进行。L和Y在游戏初期只能从1唱数到20,从10倒数到1。随着干预次数的增加,L和Y逐渐能够正确地从1唱数到50,从20倒数到1的正确率也明显提高。L与Y在“数字连线”游戏中的表现详见表3。
(二)关于数的部分与整体关系
本研究在开始“数的组成和分解”干预之前,采用林嘉绥设计的“数的部分与整体关系”和“数的组成和分解”测查方案〔20〕考察被试儿童对数的部分与整体概念的理解水平。“数的部分与整体关系”测查主要考察儿童是否理解以下三方面内容:(1)一个总数分为两个部分数,其总数不变,即B=A+A'。(2)两个部分数之间存在着互补的关系,即B=(A-n)+(A'+n)。(3)两个部分数之间存在互换关系,即B=A+A'=A'+A。每项测验可分为三个操作水平:完全不理解、通过直觉或尝试错误后作出正确判断、完全掌握。“数的组成和分解”测查分“口头”和“实物”两个水平,也可分为三个操作水平:完全不会组成或分解、只会部分组成或分解、完全会组成或分解。L和Y的各项测验前测水平见表4。
由表4可知,在“数的部分与整体关系”方面,L已能够完全掌握并说出原因;Y的理解水平较低,后两项虽然判断正确,但仍需要借助实物和数字进行推理。在“数的组成和分解”方面,无论是L还是Y,“口头”水平的正确数量都少于“实物”水平,且在回答过程中随机性较明显。
“数的组成和分解”干预分成四个阶段:(1)开始时,先进行3次“藏珠子”游戏。把游戏的主动权完全交给儿童,让他们在游戏中自由探索各种问题解决的方法。(2)随后,进行3次“小熊捉迷藏”游戏,让儿童体会“数的分合”,研究者还通过逐一增加“躲进山洞”的小熊数量,让儿童感受“数的分合”规律。(3)接下来进行5次“小熊请客”游戏,逐步提高难度(从小熊数量和是否允许动手操作两个方面),引导儿童利用书面符号记录发现“数的分合”规律(包含关系、互补关系、互换关系),并尝试运用规律有顺序、不遗漏地穷尽某个数字所有的分解与组合方法。(4)最后进行6次“数数棒”游戏,让儿童通过目测估算,理解并运用“数的分合”知识(如以8号棒为参照,判断6号棒需要加上几号棒的长度,才能和8号棒等长)。整个干预过程中,研究者着重引导被试儿童自我建构与体验,不直接告诉儿童也不急于要求儿童给出答案。具体过程举例如下。
研究者:今天小熊想邀请5位朋友来家里做客,但家里空间小,一次不能请太多小熊来家里玩,最好分两次邀请小熊。你能帮我想想有什么好办法吗?(研究者通过讲故事创设问题情境,同时也以参与者的身份加入到游戏过程中,与L建立起学习共同体。)
L:让我来想想办法……可以先邀请3只小熊,再邀请2只小熊(L一边说一边把小熊分成相应数量的两队)。
研究者:你的方法很棒!帮主人解决了一个大问题。我们把这个好办法记录下来吧(引导L在记录纸上进行记录)。
(如此循环进行,直至穷尽5的所有分解方法。)
研究者:今天我们帮了小熊一个大忙,想出了很多好办法。请你看一看记录纸,自己分析分析,有没有发现什么规律?(通过启发提问,引发认知冲突,引导L结合已有记录进行思考。)
L摇头表示没有发现。(此时,研究者并没有急于告诉L正确答案,而是耐心等待L的顿悟。终于,在几次游戏之后,L自己报告说:第一次请的小熊多的话,第二次请的小熊就少了,因为没有那么多小熊了。)
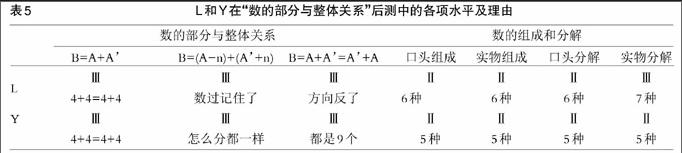
在全部干预结束之后,再次考察被试儿童对“数的部分与整体关系”的理解水平。L和Y各项测验后测水平见表5,与前测相比进步明显。
三、干预结果
干预结束时,L与Y已经能够较为熟练地从1唱数到50、从20倒数到1,“双向数链”水平的数字范围扩展到1~20;能够完全理解“数的部分与整体关系”,基本掌握10以内“数的组成与分解”。
在TEMA后测中,L原始分为42分,能力分为115(进步了11分);Y原始分为42分,能力分为105(进步了16分)。其中,L在干预结束时已接近正常组均分,与正常组均分的差距由21分缩小到5分;Y在干预结束时已接近数困组均分,与正常组均分的差距也由3个标准差缩小到近1个标准差。
四、讨论
已有研究总结出儿童对“数的分合”的学习路径:积累“量的分合”经验——从“量的分合”到“数的分合”——领会数的分合规律——掌握数的分合关系——用推理的方法学习分合。〔21〕本研究也基本按照这样的学习路径开展干预,并证实了干预的有效性。
然而,这样的学习路径并不完全适用于数学学习困难儿童。数学学习困难儿童因对“阿拉伯数字系统”的掌握没有正常儿童熟练,因此必须在进行“数的分解与组合”干预之前帮助他们掌握“数字系统”。研究结果提示,完善“数字系统”——积累“数的分合”经验——发现“数的分合”规律——运用“数的分合”知识,这样的干预路径可能对不同程度数学学习困难儿童均是有效的。
研究发现,儿童理解并记住个位数的加减组合规律,需有一个较长的时间过程。儿童是在理解的基础上记住这些组合的答案的,一味强调速度、机械背诵会产生不良后果。为儿童创设有目的的练习情境,有利于促进儿童对数的组合知识的掌握。〔22〕本研究在干预过程中,通过游戏创设了真实的问题情境,并且遵循了儿童对“数的部分与整体关系”的理解和掌握规律,耐心等待儿童通过游戏和操作进行自我意义建构,这可能是本研究干预效果较为理想的原因之一。
参考文献:
〔1〕周欣,赵振国,李娟,等.认知因素对儿童早期数学学习困难的影响〔J〕.学前教育研究,2013,227(11):3-13.
〔2〕JORDAN N C,GLUTTING J,DYSON N,et al.Building kindergartenersnumber sense:A randomized controlled study〔J〕.Journal of Educational Psychology,2012,104(3).
〔3〕MORGAN P L,FARKAS G,WU Q.Kindergarten childrens growth trajectories in reading and mathematics:Who falls increasingly behind〔J〕.Journal of Learning Disabilities,2011,44(5):472-488.
〔4〕JORDAN N C,KAPLAN D,RAMINENI C,et al.Early math matters:Kindergarten number competence and later mathematics outcomes〔J〕.Developmental Psychology,2009,45(3):850-867.
〔5〕〔10〕GEARY D C,HOARD M K,NUGENT L,et al.Mathematical cognition deficits in children with learning disabilities and persistent low achievement:A five-year prospective study〔J〕.Journal of Educational Psychology,2012,104(1).
〔6〕李正清,周欣,康丹,等.大班数学学习困难儿童的个案干预研究〔J〕.幼儿教育:教育科学,2013,591/592(7/8):10-16.
〔7〕GINSBURG H P,BAROODY A J.Test of early mathematics ability〔M〕.Austin:Pro-Ed,2003.
〔8〕康丹,周欣,田丽丽,等.《早期儿童数学能力测试(中文版)》对上海市5~6岁儿童的适用性研究〔J〕.幼儿教育:教育科学,2014,622(6):39-45.
〔9〕〔12〕〔13〕〔18〕〔19〕〔22〕周欣.儿童数概念的早期发展〔M〕.上海:华东师范大学出版社,2004:2.
〔11〕GEARY D C,BAILEY D H,HOARD M K.Predicting mathematical achievement and mathematical learning disability with a simple screening tool:The number sets test〔J〕.Journal of Psychoeducational Assessment,2009,27(3):265-279.
〔14〕〔20〕林嘉绥.儿童对部分与整体关系认识发展的实验研究〔J〕.心理学报,1981,(2).
〔15〕〔16〕NELSON G. Math at their own pace:Child-directed activities for developing early number sense〔M〕.St Paul:Redleaf Press,2007.
〔17〕东方沃野.数数棒〔M〕.南昌:江西高校出版社,2010.
〔21〕彭小元.基于幼儿学习路径重新审视“数的分合”教学〔J〕.幼儿教育,2013,569/570.
A Case Study of Mathematical Game Intervention for 5-6 year-old Children with Mathematical Learning Difficulty
Li Zhengqing1, Zhou Xin2, Tian Lili2, Kang Dan3, Xu Jingjing4
(1University of Denver, Denver, 80208)
(2Faculty of Education, East China Normal University, Shanghai, 200062)
(3College of Educational Science, Hunan Normal University, Changsha, 410006)
(4Shanghai Punan Kindergarten, Shanghai, 200120)
【Abstract】This research engaged two 5-6 year-old children with mathematical learning difficulties to explore the effects of mathematical game intervention on number skills of “number words” and “part-whole relationship”. After the intervention, childrens number skills were enhanced more or less. It suggests that the intervention trajectory including perfecting number words, accumulating number experience of separation and reunion, discovering number rule of separation and reunion, applying number knowledge of separation and reunion, might be effective to help MLD childrens understanding of “part-whole relationship”.
【Keywords】children with early mathematical learning difficulties; game intervention; individual case

