罗文大桥拱肋吊装线形控制与测量技术

黄海勇 林用祥

（中铁二局第五工程有限公司 四川成都 610091）

罗文大桥拱肋吊装线形控制与测量技术

黄海勇 林用祥

（中铁二局第五工程有限公司 四川成都 610091）

罗文大桥造型新颖，施工难度较大，其中钢箱拱的吊装测量定位是其难点之一。本文通过介绍罗文大桥钢箱拱肋的吊装的工程实例，阐述了系杆拱桥拱肋吊装测量定位及线形控制的相关测量技术，对系杆拱桥拱肋吊装有一定参考意义。

罗文大桥；钢箱拱吊装；线形控制；测量技术

前言

随着我国经济的快速发展，对桥梁的安全、跨度、美观等方面都提出了更高的要求。系杆拱桥因其承载力大、跨度大、造型美观等优点越来越受到人们的青睐。在系杆拱桥施工中拱的线形控制是其关键技术之一。根据测量控制测量原理及桥梁技术规范要求，运用不量仪高测三角高程、坐标转换建立独立的三维坐标系统、三维坐标法等测量技术，可以快速、准确的达到控制拱肋线形的目的，且满足精度要求。

1 工程概况

1.1 主桥整体布置

罗文大桥北起罗文大道与石埠路的相交路口，南接五一路延长线与罗文大道延长线路口，路线全长1408.522m，其中主桥长460m，宽41.5m，采用[50m+2×180m+50m]海鸥式拱桥；主拱肋由三角刚架混凝土拱肋段和主跨钢箱拱肋段组成，东西分别有两条拱肋（全桥共四条拱肋），分别位于各自的竖直平面内，桥面上拱肋间没有任何横向联系。主桥总体效果图如图1。

图1 罗文大桥主桥总体效果图

1.2 拱肋线形设计

拱肋由钢箱拱肋段和混凝土拱肋段组成，拱轴线是由矢高为52m，跨径180m的二次抛物线形成的。拱轴线坐标按下式计算：

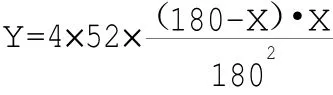
拱肋截面径向高度由X=31.25m时的3.96m，到拱顶的2.7为钢拱肋段；拱肋截面径向高度按二次抛物线进行变化。拱肋截面径向高度按下式计算：m

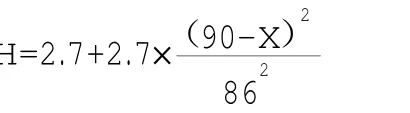
拱轴线的理论计算原点是拱座对称中心线上高程为68.3m点，示意图如图2。

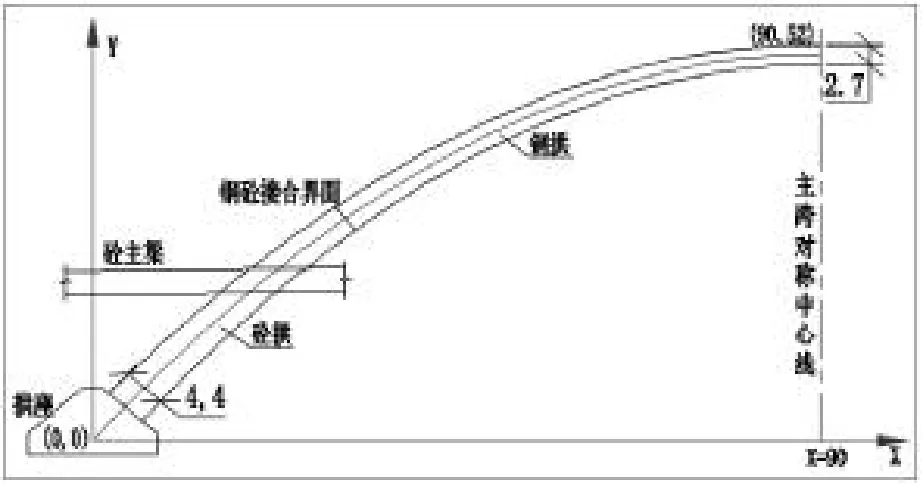
图2 拱肋线性控制坐标示意图

2 拱肋线形分析

由于拱轴线是一虚拟线，不能用来直接定位拱肋，现场测量定位点主要是拱肋的上缘和下缘，因此，需要对拱轴线性进行分析，使其能计算任意拱肋截面上的上缘和下缘坐标，以便现场进行定位安装。

拱轴线与上缘及下缘的关系图如图3。

图3 拱轴线与上下缘关系示意图

在图3中：P点为任意截面拱轴的中心点，EF为水平方向线，AB为拱轴线上的点P点对应的切线。

根据图3中的关系，由拱轴线方程求导可得其切线方程为：

由图3可得拱肋上缘和下缘的坐标计算式为：

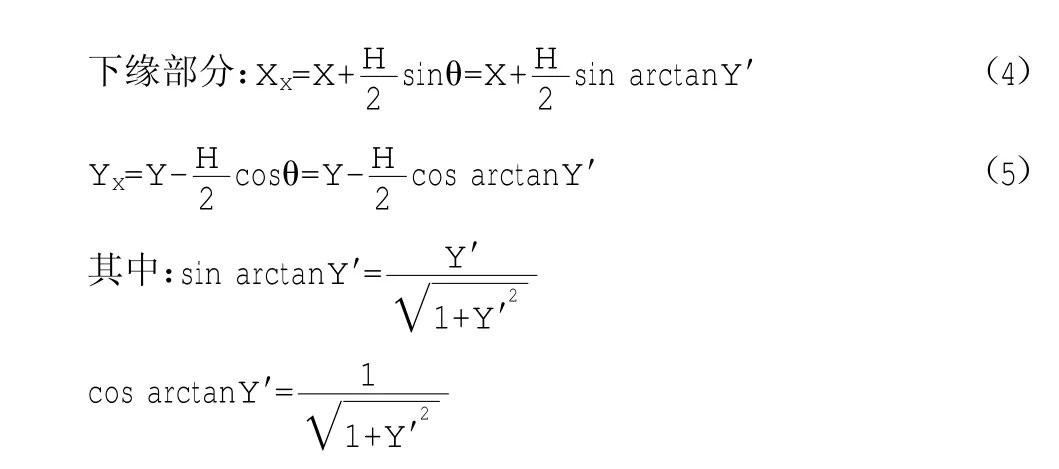
将已知参数代入公式（2）（3）（4）（5）中可得任意截面拱肋上下缘坐标的计算公式：

为方便在现场进行计算，可将公式（6）（7）（8）（9）编入卡西欧fx-5800P计算器，能快速准确的计算出任意截面拱肋的上下缘坐标。经与设计坐标验证，利用卡西欧fx-5800P计算器计算出的结果与设计误差极小，可忽略不计。

3 测量控制网的建立及坐标转换

3.1 测量控制网的建立

罗文大桥工程统一采用1954年北京坐标系和1956年黄海高程系。

罗文大桥采用“缆索吊机原位吊装、斜拉扣挂”施工方案，对测量控制的精度要求很高，因此建立一个能够满足施工控制精度要求的桥梁测量控制网尤为重要。开工前，经理部在区勘测院所给控制网的基础上，又委托中铁二局股份有限公司测量队对罗文大桥控制网进行了加密及复测。通过复测成果显示，控制网的精度非常高，完全能满足现场施工的需要。

测量组将在使用桥梁控制点位的过程中定期对各控制点位之间的几何关系，边长及相对高差进行复核，确认点位无误，无位移方可使用。

3.2 坐标转换

为准确、快速地计算出拱肋上任意点的坐标并与设计坐标比较，指导现场拱肋调整，结合现场实际情况需要，拟将罗文大桥的平面控制坐标（54北京坐标）转换到与桥轴线统一的独立坐标系中，再进行放样。

桥轴线独立坐标系以罗文大桥工程起点坐标（2525818.7323，521567.6250）作为原点O（0，0），以桥轴线为X轴（顺桥向为正），桥轴线法线为Y轴（顺桥轴线左负右正）。两坐标系间的转换可以将54北京坐标系以O为中心逆时针旋转一定角度即可转换到桥轴线独立坐标系中。两坐标系转换示意图（图4）。

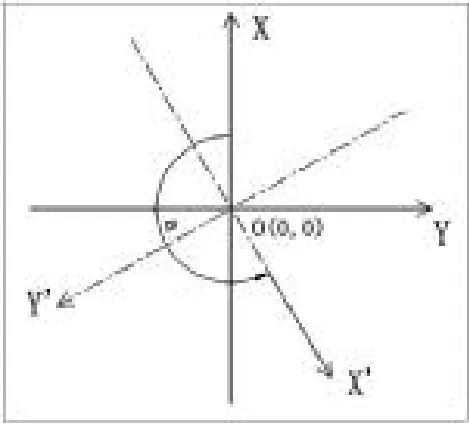
图4 两坐标系转换示意图

图4中O-XY为54北京坐标系，O-X＇Y＇为桥轴线独立坐标系，逆时针旋转角为α。

参考数学平面直角坐标系转轴公式原理可推导出工程平面直角坐标系的转轴公式：

式中：△x、△y——待求点坐标减坐标原点坐标（54北京坐标）；

通过公式（10）可以计算任意坐标在桥轴线独立坐标系中对应的相对坐标，且桥轴线独立坐标X、Y坐标分别对应罗文大桥的里程、偏距。在现场实际操作中，将公式（10）编入卡西欧fx-5800P计算器中，能快速计算出所需数据，可以大大提高钢拱肋的调整效率，降低错误的概率。

4 钢箱拱吊装过程中的测量控制

4.1 钢箱拱吊装测量控制要点

（1）拱肋平面位置即拱轴线的控制；

（2）拱肋标高的控制；

（3）拱脚、钢帽、塔架及已调拱肋节段的定期观测。

其中拱肋的平面位置及标高控制是重点，须严格按照《工程测量规范》（GB50026-2007）及《公路桥涵施工技术规范》（JTGTF-50-2011）相关要求。项目部要求钢箱拱平面安装偏差≤10mm，高程安装偏差≤±10mm。

4.2 拱肋平面位置及高程的控制

为保证拱肋加工及安装精度，钢拱肋在出厂前要进行整体预拼，预拼的精度高低是确保拱肋线形正确的最有力措施。

拱肋安装测量控制总体思路为：拱肋初步就位后利用前方交会粗调，之后利用厂家预拼的点位和无脚架小棱镜实测拱肋三维坐标进行精调，直至调整到规范允许误差范围内。钢拱肋安装测量控制流程如下；

起吊→前方交会初步定位→测量控制点三维坐标→根据监控指令精调→安装、张拉扣索→松主索→复测→焊接→复测→准备下一节段安装。

在拱肋调整的过程中，特别是工况变化时要加强拱脚、钢帽、塔架及已调拱肋节段的观测，在确保安全准确的情况下才能指导现场的下一工序施工。

4.3 拱肋测量控制精度的保障措施

4.3.1 不量仪器高、棱镜高测三角高程

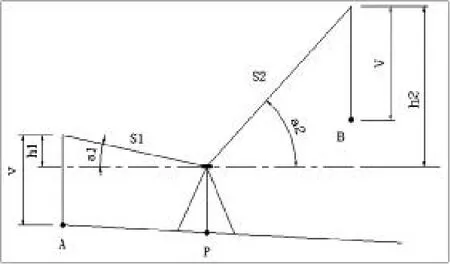
图5 不量仪高测三角高程示意图

如图5中，为测B点的高程，在P控制点架设仪器，在A点安置棱镜，测得PA间距离S1与垂直角a1，从而计算出P点处全站仪的视线高程为：

其中V为棱镜高。

然后将棱镜不改变其棱高架设到B点，同样测得PB间距离S2和垂直角a2，得出P点处全站仪的视线高程为：

将（11）（12）合并可得Hp=HA+V-h1=HB+V-h2，消掉棱镜高V可得：

从（13）式中看出，待测点B点的高程计算时已不存在全站仪仪器高与棱镜高，从而避免了因量取仪高所产生的人为误差，提高了高程的测量精度。但此方法的使用过程中要保证使用同一棱镜且不能改变其棱镜高。

4.3.2 安装中预拱度、温度、气压等修正

钢拱肋在吊装过程中，外界温度、气压、风力、湿度等会对测量结果产生影响，因此需时刻观测上述指标，根据变化调整全站仪中的各参数。

温度的修正包括两个方面：①全站仪中温度的设置及系数修正；②监控单位对每节拱肋都提供了标高均匀修正系数（基准温度为20℃），在现场调整过程中需将温度引起的标高变化进行均匀温度修正。钢拱肋的调校应避免日照温差的影响，宜选择温度稳定时进行。

4.3.3 坐标转换后，提高效率，降低错误概率

将厂家预拼点位的就位三维坐标转换到桥轴线独立坐标系中后，能在现场快速、准确的给出拱肋调整的具体偏差数据，大大缩短了拱肋定位的时间，并能降低错误概率。以往的常规做法是直接用大地坐标进行放样，不仅数据处理复杂、费时，而且由于桥轴线与大地坐标往往存在夹角，造成调校方向与桥轴线方向不统一，会加大现场拱肋调校的难度。

经过实践表明，建立独立坐标系，转换坐标后进行一些空间构造物测量定位的方法不仅仅可以用于拱肋的调校，对于梁、空间曲线拱肋、空间曲线梁等的调校都非常适用，只是要针对构造物的不同线形而全面、综合考虑，设计相应的独立坐标系统。

4.3.4 拱肋合拢段合拢前72h连续观测

由于钢绞线、钢拱等材料受温度变化会产生一定的徐变，能否掌握其中的变化规律并提前加以修正是拱肋能否精确合拢的关键。为此，在拱肋合拢前对合拢口进行频率为每2h一次的72h（3d）连续观测，通过采集现场实际测量数据，以取得钢拱肋合拢口长度随温度变化的相关规律，指导合拢段的切配及精确安装。

观测采用钢尺和全站仪测量两种方法，以前者为主，全站仪数据供参考。钢尺需检定合格且测量数据需进行修正。为方便合拢段的切割，观测点选择拱肋四个角点，下游顶角、上游顶角、下游底角、上游底角分别编号A、B、C、D。图6是根据P10～P11间上游拱肋合拢前的24h（1d）观测数据绘制的钢拱随温度变化的趋势图（如图6）。

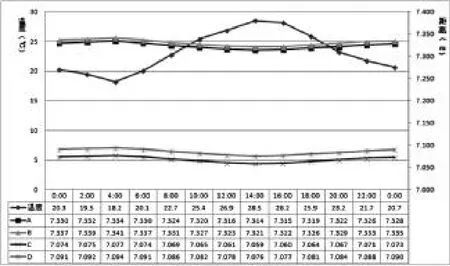
图6 P10～P11上游拱肋合拢前拱肋随温度变化趋势图

根据设计及施工方案要求，拱肋合拢需在温度稳定时进行，宜选择在夜间温度为20℃左右。通过72h观测数据可知，夜间22：00～2：00间温度适宜且稳定，合拢口长度变化较小，适合拱肋合拢。可靠、准确的测量数据和科学的施工组织方案，保证了全桥四个钢拱均一次性合拢成功。

5 钢拱肋合拢

全桥四个拱肋全部合拢后，在合适的温度（20℃）下对合拢段三维坐标进行复测，并与设计坐标进行比较，得出差值，如表1。

从表1中数据分析可知，钢拱肋合拢后的三维坐标误差均在设计误差以内，符合设计要求。

6 结语

（1）不量仪器高、棱镜高测三角高程在本工程的运用是成功的，避免了因量取仪高所产生的人为误差，提高了高程的测量精度。

（2）建立适合本工程的独立三维坐标系统，所测三维坐标数据能直接反映出拱肋的空间位置关系，使测量数据清晰，计算、分析简单，现场拱肋调节准确、高效。

（3）拱肋合拢前对合拢口进行72h（3d）连续观测，采集了大量可靠、准确的现场数据，从而掌握了拱肋随外界条件变化的规律，为拱肋一次性成功合拢提供了理论数据保障。

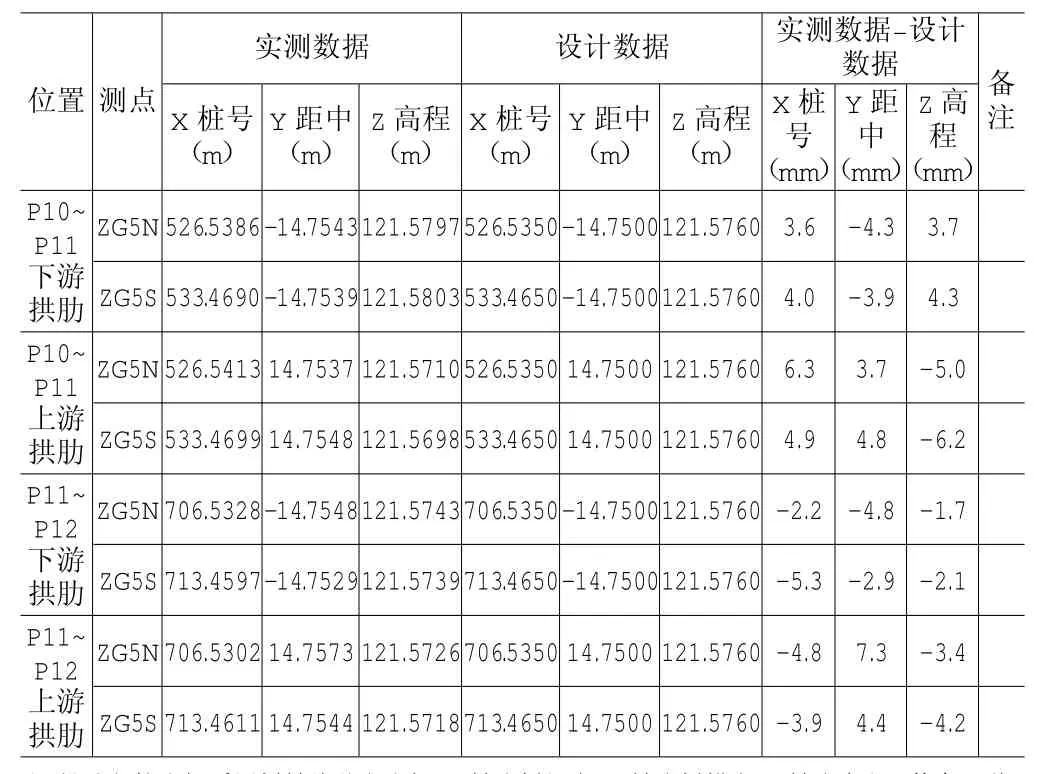
表1 罗文大桥拱肋合拢三维坐标复测表

[1]《工程测量规范》（GB50026-2007）[S].

[2]《公路桥涵施工技术规范》（JTG/TF50-2011）[S].

[3]张仰燖，等.不量仪器高、棱镜高的三角高程测量[J].测绘通报，2002.

[4]张延寿.铁路测量[M].成都：西南交通大学出版社，1995.

U442

A

1673-0038（2015）35-0330-04

2015-7-20

黄海勇（1989-），男，助理工程师，本科，主要从事桥梁工程施工技术方面的工作。

林用祥（1972-），男，高级工程师，本科，主要从事桥梁工程方面的工作。