YKR型振动筛筛体运动及物料透筛概率分析

杨淑琳，赵三星

（武汉科技大学机械自动化学院，湖北 武汉，430081）

YKR型振动筛是工矿企业常用的粒度分级筛分设备，其独特的外置式偏心块结构使筛体的运动轨迹可根据偏心块质量的调整发生改变。筛体的运动会对筛面上物料的运动产生很大的影响，研究筛体的运动及其对筛面上物料运动的影响，可为振动筛的设计及指导现场生产提供理论依据。目前对物料透筛概率的研究多采用通过试验对 Weibull模型进行拟合的方法［1－2］，本文则从物料单颗粒透筛概率和颗粒在筛面上的跳动次数两个因素对物料透筛概率进行研究，以期为预测物料透筛概率和优化筛机运动参数提供依据。

1 振动筛运动仿真分析

1.1 数学模型的建立

图1 振动筛力学模型Fig.1 Mechanical model of vibrating screen

建立图1所示的振动筛力学模型，固定坐标原点O在筛体质心处。图1中，M为筛体质量；m0为偏心块质量；Lx1、Ly1、Lx2、Ly2分别为入料端、排料端相对于质心的坐标值；L0为偏心块相对于质心的纵坐标；K1、K2为支撑弹簧；A、B分别为入料端、排料端位置。

由于YKR型振动筛的激振器布置在质心上方，其激振力和弹簧作用力均不通过质心，所以筛机的运动有3个自由度：沿X、Y方向的位移以及绕质心的转动。

采用拉格朗日方程法建立筛机的振动微分方程如下：

式中：x、y为筛机质心沿X、Y 轴的位移；CKx1CKy1、CKx2、CKy2为支撑弹簧 K1、K2的横向、纵向阻尼，N·s／m；lx1、ly1和lx2、ly2分别为支撑弹簧K1、K2到质心沿X、Y 方向上的距离，m； 为筛机转角；r为偏心块半径；ω为偏心块转速；t为时间；J为筛机转动惯量，kg·m2；J0为偏心块的转动惯量，kg·m2；Kx1、Ky1和 Kx2、Ky2分别为支撑弹簧 K1、K2的横向、纵向刚度，N／m；lox、loy为偏心块回转轴轴心到质心沿X方向和Y方向的距离，m。

方程（1）的稳态解为

式中：xa、xb为筛机X方向上的位移沿正弦、余弦方向的分量；ya、yb为筛机Y方向上的位移沿正弦、余弦方向的分量；a、b为筛机转角沿正弦、余弦方向的分量。

由式（2）可求得筛机X、Y 方向的振幅λx、λy及转角幅值 为

从式（4）可以看出，筛体上任意一点处Y方向的振幅与这一点的横坐标相关，X方向的振幅与这一点的纵坐标相关。

1.2 仿真方法

弹簧水平刚度与竖直刚度的比例系数为0.5［4］，取阻尼比ξ＝0.08，计算弹簧阻尼。根据厂商提供的筛机参数及计算结果，振动筛相关参数如表1所示。

表1 YKR型振动筛的参数Table1 Parameters of YKR circular vibrating screen

将振动微分方程式（1）写成矩阵形式：

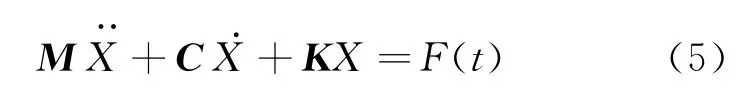
式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；X为筛机位移；F（t）为激振输入。

选取状态变量Z及输出变量Y，则可将式（5）转化为状态空间表达式：

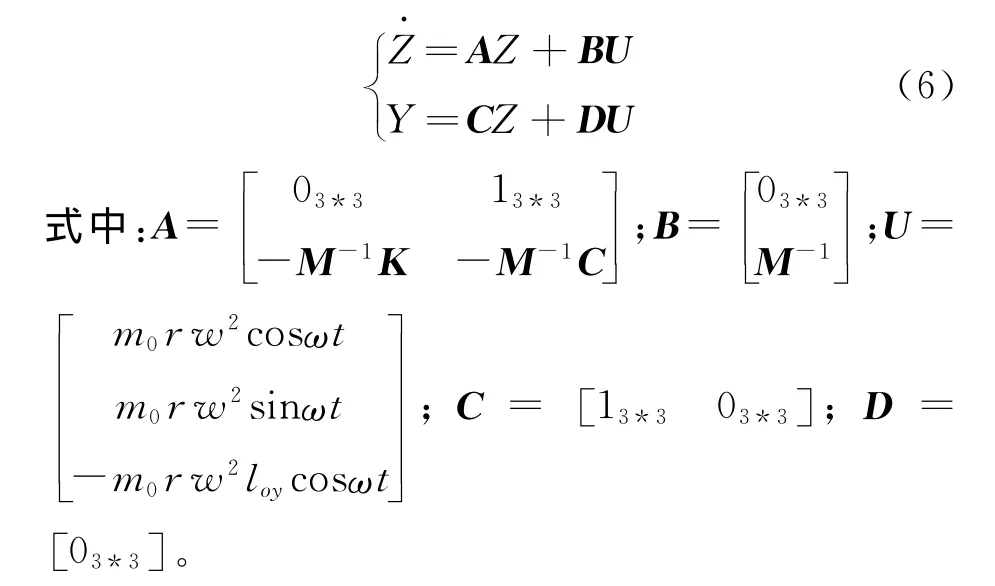
［4］中的方法，利用Matlab／simulink中的State－Space模块建立图2所示的仿真模型。设定仿真时间为0～4s，采用ode4定步长算法，设定步长为0.002s，设置XY scope中的坐标幅值后，运行仿真。

图2 系统仿真模型Fig.2 Simulation model of the system

1.3 仿真结果与分析

仿真得到振动筛筛体质心沿X、Y轴方向的位移曲线及质心转角曲线如图3所示。由图3中可以看出筛体启动0～4s间其质心在3个自由度方向的振动由瞬态到稳态的变化过程：筛体在启动后发生扰动，振幅明显增大，到3s后开始进入稳定工作状态。

图4所示为振动筛质心的运动轨迹。由图4中可以看出，振动筛进入平稳振动后，筛体质心处的运动轨迹近似呈圆形。

图3 质心的位移及转角曲线Fig.3 Displacement and rotation angle curves of the centroid

图4 质心运动轨迹Fig.4 Trajectory of the centroid

由式（4）计算可得稳定状态下筛机的入料端A（1.2，0.4）和排料端B（－0.7，－1.0）的运动轨迹，结果如图5所示。由图5中可以看出，振动筛进入平稳振动后，筛体入料端与排料端运动轨迹均为椭圆，两个椭圆形轨迹在筛体上呈正八字形，这种运动轨迹对物料的运动及物料的透筛概率有直接的影响［5］。

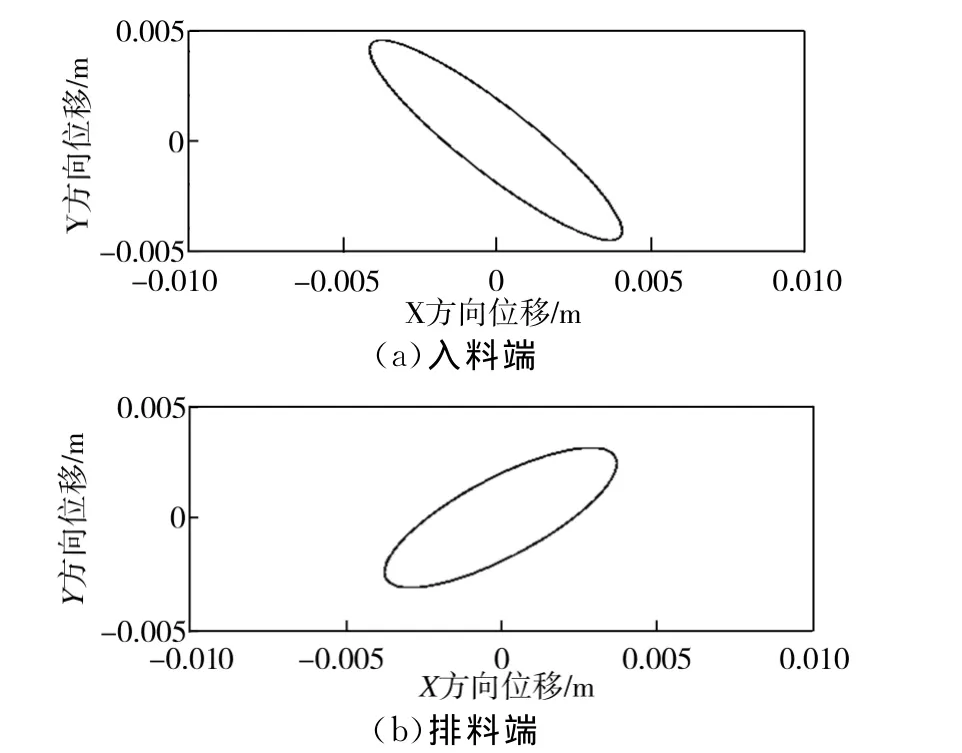
图5 入料端与排料端运动轨迹Fig.5 Trajectories at the inlet and outlet

2 物料运动分析

振动筛上物料的运动速度V按经验公式［6］计算：

式中：KQ为修正系数，取决于筛机生产率；n为振动次数，次／min；λ为振幅，m；g为重力加速度，m／s2；α0为筛面倾角，对于圆运动振动筛，通常取α0＝15°～30°［6］，本文取α0＝18°。

根据振动筛入料端、质心、排料端的振幅，计算物料在筛面上的速度变化曲线，结果如图6所示。

图6 物料在不同方向的速度变化曲线Fig.6 Velocity curves of the material in different directions

入料端坐标为（1.2，0.4），排料端坐标为（－0.7，－1.0），则由图6中可以看出，物料从入料端到排料端，垂直方向的速度变大，水平方向的速度变小。在入料端，沿水平方向速度大可加快物料松散、分层，在排料端，沿水平方向运动速度小可增加物料透筛概率［6］，实现高效筛分。

3 物料透筛概率分析

筛面上物料每跳动一次只有两个可能，透筛或不透筛，即每跳动一次相当于一次独立的试验，那么物料颗粒透筛概率的计算就相当于N重贝努利试验，设颗粒透筛概率为Cx，颗粒跳动次数为m，则物料在整个筛面上的透筛概率P［7］为：

由式（8）中可知，物料在整个筛面上的透筛效率取决于颗粒的透筛概率及颗粒在筛面上的跳动次数。

3.1 颗粒透筛概率

颗粒透筛概率按Mogenson公式计算［8］：

式中：s为颗粒相对粒度，即物料粒度与筛孔尺寸之比；a为筛孔尺寸，mm；b为筛丝直径，mm；β为颗粒对筛面的相对运动方向线与垂直线的夹角，（°）。

式（9）中β的计算公式［8］为

式中：φd抛始角，即物料开始抛掷时筛面的振动相位角，（°）；φz抛止角，即物料抛掷结束时筛面的振动相位角，（°）；θ为抛离角，即物料开始抛掷与结束抛掷时的振动相位角之差，（°）。

式（10）中，抛止角、抛离角可根据筛机抛掷指数 D 计算［3］。

筛机不同位置处的颗粒透筛概率计算结果如图7所示。由图7中可见，物料中单颗粒在排料端与入料端的透筛概率变化趋势相同，但相对粒度相同的物料在排料端的透筛概率比在入料端的透筛概率大；在质心处，相对粒度为0.3～0.5的物料更容易透筛。

3.2 颗粒跳动次数

颗粒跳动次数m取决于物料的运动速度［5］，物料的运动速度又与筛机的振幅有关。物料振动次数与筛机振幅的关系如图8所示。由图8中可见，物料跳动次数随筛机X方向振幅变化的幅度较小，随筛机Y方向振幅变化的幅度较大，表明物料透筛概率主要取决于筛机Y方向的振幅，并且当Y方向的振幅为0.003～0.004m时，物料的跳动次数最多，有利于颗粒透筛。

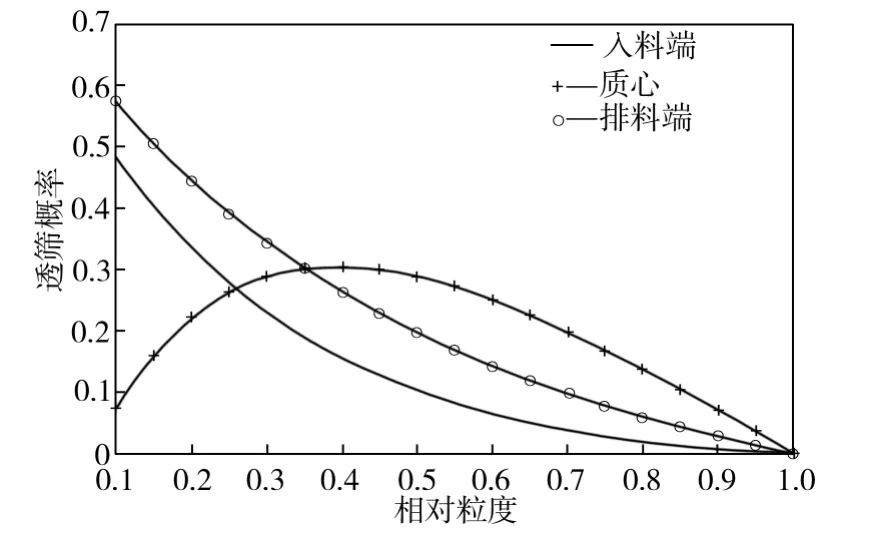
图7 单颗粒物料透筛概率Fig.7 Screen－penetrating probability of the single－particle material

图8 颗粒跳动次数与筛机振幅的关系Fig.8 Relationship between jumping time of particles and amplitude of the screen machine

3.3 物料透筛概率

忽略X方向的振幅对跳动次数的影响，由图4、图5中可知入料端、质心、排料端Y方向的振幅分别为0.005、0.006、0.0033m，再由图8（b）可查得相应位置处物料的跳动次数分别为7、6、15次，则根据式（8）计算可得到物料在不同位置处的透筛概率，结果如图9所示。由图9可知，细粒级物料在入料端透筛概率最大；大部分物料在质心区域透筛；透筛概率随着物料粒度的增大而减小；难筛物料在排料端不能透过筛孔，将排出筛体。由此可知，沿振动筛筛长方向不同位置处可得到不同粒度级的筛分产品。

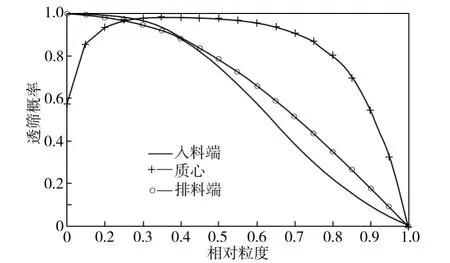
图9 物料透筛概率Fig.9 Screen－penetrating probability of materials

4 结论

（1）YKR型振动筛物料在筛面上的运动，从入料端到排料端沿垂直方向速度加快，沿水平方向速度减小。

（2）排料端物料颗粒透筛概率比入料端颗粒透筛概率大，质心处相对粒度为0.3～0.5的颗粒透筛概率最大。

（3）物料的跳动次数主要与筛面垂直方向振幅有关，可通过改变筛面垂直方向的振幅增加颗粒的跳动次数。

（4）物料运动以及透筛概率的不同使得沿振动筛筛长方向不同位置处可得到不同粒度级的筛分产品。

参考文献

［1］焦红光.振动筛分过程解析［M］.北京：煤炭工业出版社，2008：22－23.

［2］赵跃民，刘初升.干法筛分理论及应用［M］.北京：科学出版社，1999：9－13.

［3］闻邦椿，刘凤翘，刘杰.振动筛 振动给料机 振动输送机的设计与调试［M］.北京：化学工业出版社，1989：139.

［4］张楠，侯晓林，闻邦椿.基于动态优化设计方法振动筛设计的研究［J］.煤矿机械，2008，29（3）：12－15.

［5］曾德惠，黄松和.基于 Matlab／Simulink的多自由度机械振动系统仿真［J］.湖北民族学院学报：自然科学版，2008，26（1）：57－60.

［6］沈惠平，张会芳，张江涛，等.并联运动振动筛的筛分运动规律及其轨迹的研究［J］.机械设计，2008，25（12）：20－24.

［7］张文斌，张龙全，孙少华，等.风筛式清选装置中农业物料透筛概率的研究［J］.农机化研究，2009（8）：50－53.

［8］闻邦椿，刘树英，何勍.振动机械的理论与动态设计方法［M］.北京：机械工业出版社，2002：1－5.