上证380高频指数数据已实现GARCH（1，2）模型的风险测量

魏正元，张　鑫，赵　瑜（重庆理工大学数学与统计学院，重庆400054）

上证380高频指数数据已实现GARCH（1，2）模型的风险测量

魏正元，张鑫，赵瑜
（重庆理工大学数学与统计学院，重庆400054）

针对高频金融数据收益率序列的厚尾和偏斜性，建立了偏t误差分布假设下的R-GARCH（1，2）模型，对上证380指数5 min频率的高频数据进行了VaR预测，并与经典的正态分布和t分布误差假设下的R-GARCH（1，2）模型的预测精度进行了对比分析。结果表明，误差项服从偏t分布的R-GARCH（1，2）模型能够有效识别上证380指数收益率序列的分布特征，并且能够精确地测量其收益风险。

高频金融数据；已实现GARCH；VaR；偏t分布；厚尾特征；偏斜性

风险测量是金融市场风险管理的核心和基础［1］，准确度量和预测金融资产的收益风险有利于投资者做出正确的投资决策。目前，VaR方法已成为被金融机构和监管当局认可的最重要的金融风险管理方法之一。国内外对VaR的研究都是以低频金融数据为研究对象。随着计算机存储技术的飞速发展，采集和记录高频金融数据日趋便捷，因而对高频金融数据的研究日益受到广泛关注。金融市场的信息连续影响证券市场价格的运动过程，收集样本数据的频率越高，信息丢失就越少。由于比低频数据包含了更多的市场信息，因此基于高频数据的金融风险测量也更为准确。

在VaR的传统计算中，以GARCH类模型最为流行［2-7］，但是GARCH类模型的研究对象是低频数据。2002年Andersen［8］针对高频数据提出了“已实现”波动率，是通过加总某一频率下的日内分时数据的收益平方来得到对真实波动率的一个估计。Hansen［9］于2012年提出了一种将GARCH类结构应用到高频数据的模型，称为“已实现”GARCH模型（R-GARCH）。R-GARCH模型是在传统的GARCH模型的基础上加入了波动率的“已实现”测度，并通过一个测量方程将“已实现”波动率与真实的波动率整合起来。在预测风险时R-GARCH模型一般都假定金融收益率序列服从正态分布或t分布，但其实际收益率并不严格服从正态分布或t分布，而是具有非对称性和厚尾特征［10］，所以使用误差项服从正态分布和t分布的RGARCH模型度量市场风险时会造成风险的高估或低估。为了处理金融数据波动率表现出来的厚尾现象和偏斜现象，R-GARCH模型除了使用一般的正态分布和t分布之外，还使用偏t分布作为收益率误差项的分布。与t分布相比，偏t分布在描述收益率序列厚尾现象的同时还考虑了分布存在偏斜的可能性，所以误差项服从偏t分布的R-GARCH模型能够更好地反映出收益率的风险特性。本文使用5 min频率的高频数据，基于偏t误差分布假设下的R-GARCH（1，2）模型对上证380指数进行风险预测，并与正态分布和t分布误差假设下RGARCH（1，2）模型的VaR预测值进行比较，在一定程度上拓展了ToshiakiWatanabe的工作。

1　模型及参数估计

由图1、2可以看到，收益率的分布存在厚尾现象和波动聚集的特征。从图3收益率的样本ACF可以看出对数收益率没有显著的序列相关性。图4是收益率的绝对值的样本ACF，图5是收益率平方的样本ACF，这两幅图表明对数收益率不是序列独立的。综合以上情况，说明上证380指数的对数收益率序列｛rt｝确实是序列不相关的，但是是相依序列，说明对该收益率R-GARCH模型是一个合适的模型。又用AIC方法确定R-GARCH（p，q）模型中的p=1，q=2，因此对其波动率进行建模，并且设定R-GARCH（1，2）模型如下：

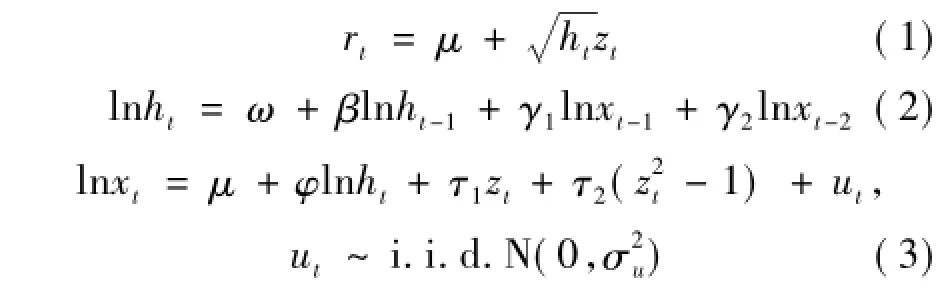
其中：rt（t=1，…，n）表示第t天的收益率；xt是第t天收益的“已实现”波动率（realized volatility）；条件方差ht=var（rtFt-1），Ft-1=σ（rt，xt，rt-1，xt-1，…）。

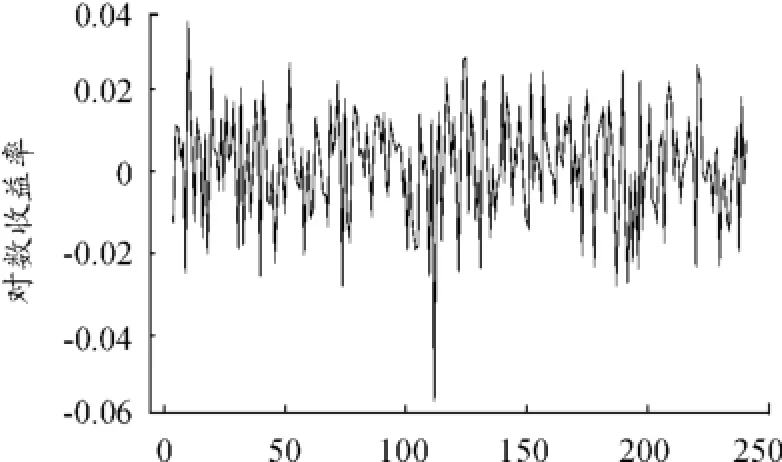
图1　上证380指数收益率分布

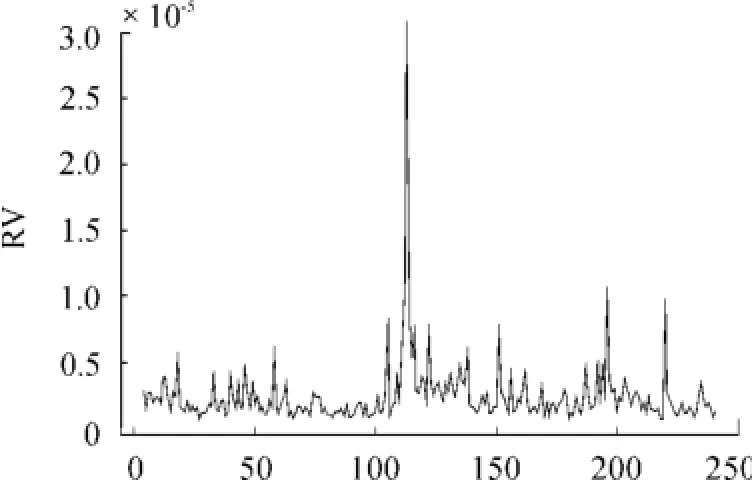
图2　5 min频率的已实现波动率

ToshiakiWatanabe估计了rt的条件期望μ≠0时的各参数值，发现μ的估计值非常小，即ht很接近于μ=0的情况，因此本文采用rt的条件期望）=0的基准模型。方程（2）是ht的动态方程，在GARCH模型中ht是ht-1和误差项zt的函数，而在R-GARCH模型中ht是ht的过去值和波动率的“已实现”测度xt的函数。测量方程（3）中的τ1zt+τ2（z2t-1）是杠杆函数，表明过去一期的收益率不仅在大小上影响波动率，也在方向上影响波动率，正的价格扰动和负的价格扰动对波动率产生不一样的影响。杠杆函数的设定与收益率误差项分布的设定相关。收益率的误差zt～i.i.d.（0，1），zt的分布也影响着模型参数估计的精确度。由于上证380指数的日收益率数据存在厚尾现象和偏斜现象，收益率误差项的分布除了考虑正态分布和标准t分布之外，还考虑偏t分布。本文使用Bollerslev（1987）的标准t分布，其形式如下：

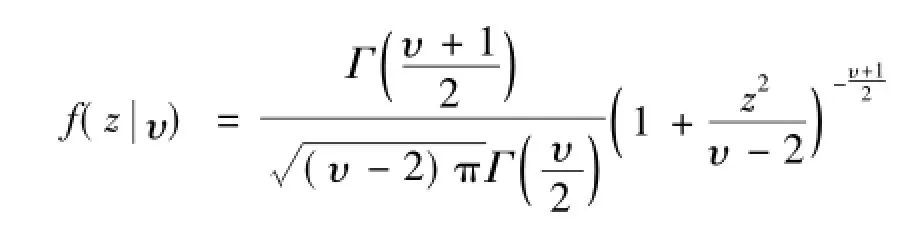
其中υ为标准t分布的自由度。在标准t分布的基础上，Hansen进一步提出了偏t分布。本文采用Fernandez and Steel（1998）的偏t分布，其形式为：

R-GARCH模型本质上是一个离散时间的随机波动率（stochastic volatility）模型，但是由于波动率“已实现”测度的存在，R-GARCH模型可以用极大似然估计将所有参数一次性估计［11-12］。对模型进行参数估计时，假定收益率rt最初的条件方差h0为无条件方差，通过式（2）迭代计算ht，然后由收益方程（1）得到收益率rt的对数似然函数，取最小值得到模型的参数估计值。

2　实证分析

上证380指数是上海证券交易所和中证指数公司于2010年11月29日正式发布的新兴蓝筹指数，它是上海市场蓝筹股指数的主要组成部分。本文采用上证380指数2013年238个交易日的5 min频率数据（数据从锐思数据库下载www.resset.cn），基于3种不同误差项分布假设下的R-GARCH（1，2）模型对我国股票市场风险进行风险预测，其收益率定义为rt=ln Pt-ln Pt-1。

记｛rt｝为上证380指数对数收益率时间序列，｛xt｝为其“已实现”波动的时间序列，分别对基于标准正态分布、标准t分布和偏t分布的R-GARCH（1，2）模型进行参数估计，得到3种模型的参数估计。

由表1的估计结果可以看出：3种模型的参数的估计值τ1和τ2符号确实是相反的，表明一般的金融资产会对负的收益率扰动做出更大的反应；偏t分布的参数ξ＞1，表明收益率的分布不是对称的而是右偏的（如图4）。根据表1中t分布的自由度υ和偏t分布的参数（υ，ξ）的估计值画出3种分布的密度函数图（图6）。

表1　基于不同分布假定下Realized GARCH（1，2）模型的参数估计结果

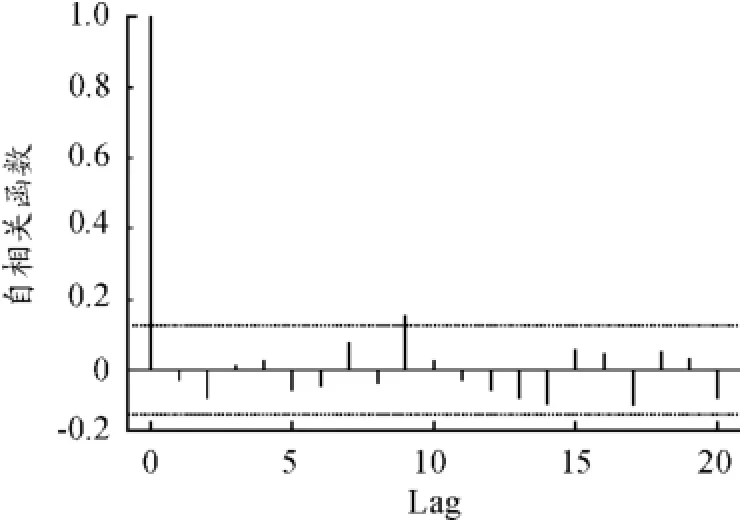
图3　上证380日收益率的自相关函数

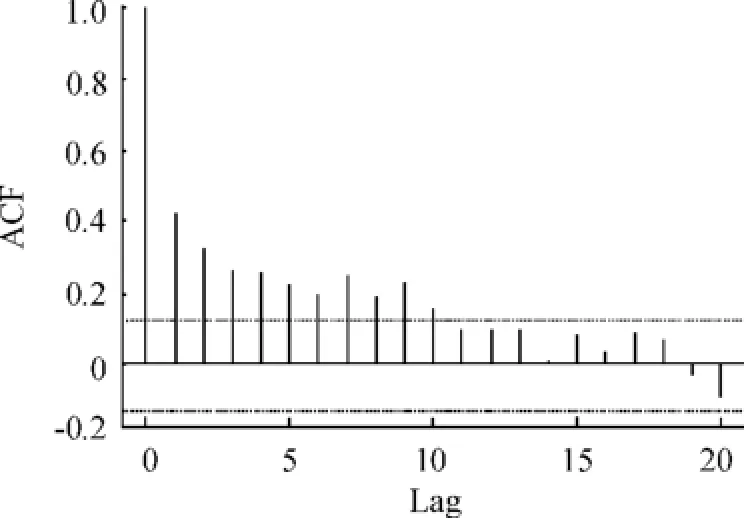
图4　上证380日收益率的绝对值的自相关函数

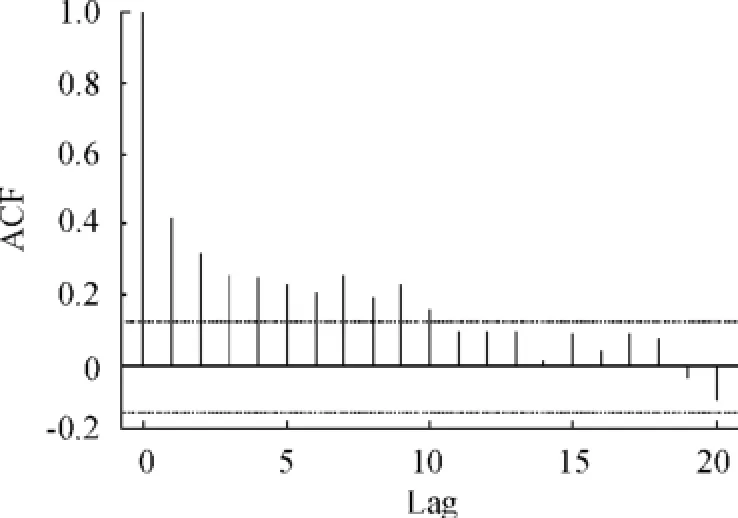
图5　上证380日收益率的平方的自相关函数

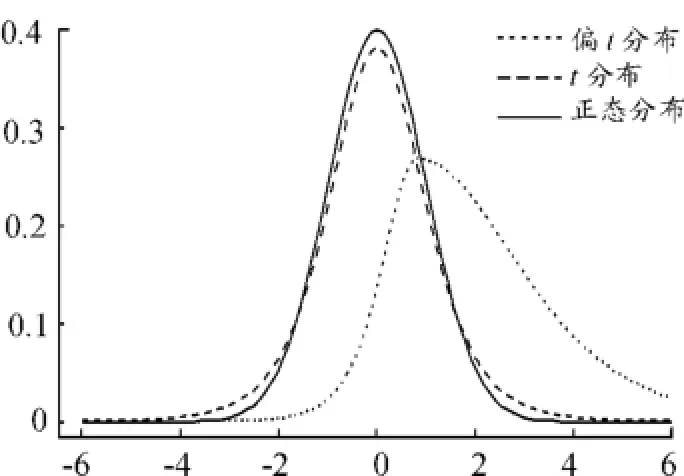
图6　不同误差项的分布

得到这些参数的估计值后将参数的估计值和最初的条件方差h0带入式（2）迭代计算h1，…，hn进行多步预测，根据分位数的线性性质计算在给定置信水平下的238个VaR值，该值给出了上证380指数在一定的置信水平下的一个上界。当实际收益率超出VaR预测值时则视为失败。表2给出了模型预测风险的失败率，可以看出：在99%、90%置信水平下，基于正态分布和t分布假设下的R-GARCH（1，2）模型的分位点估计明显偏高；在49%置信水平下，这2种模型的分位点估计偏低，都与实际情况相差很大，而偏t分布假设下的模型的溢出率接近于实际情况；在50%置信水平下，虽然3种模型的分位点估计与实际情况相差不大，但是正态分布和t分布假设下模型的预测效果没有偏t分布假设下模型的预测效果好。总之，利用偏t分布假设下的R-GARCH模型对金融市场进行风险度量得到的VaR值比正态分布和t分布假设下R-GARCH模型得到的VaR值更加稳健、精确。以上的实证分析表明：正态分布和t分布假设下的的R-GARCH模型并不适合金融市场，而偏t分布假设下的R-GARCH模型是一个合适的模型。

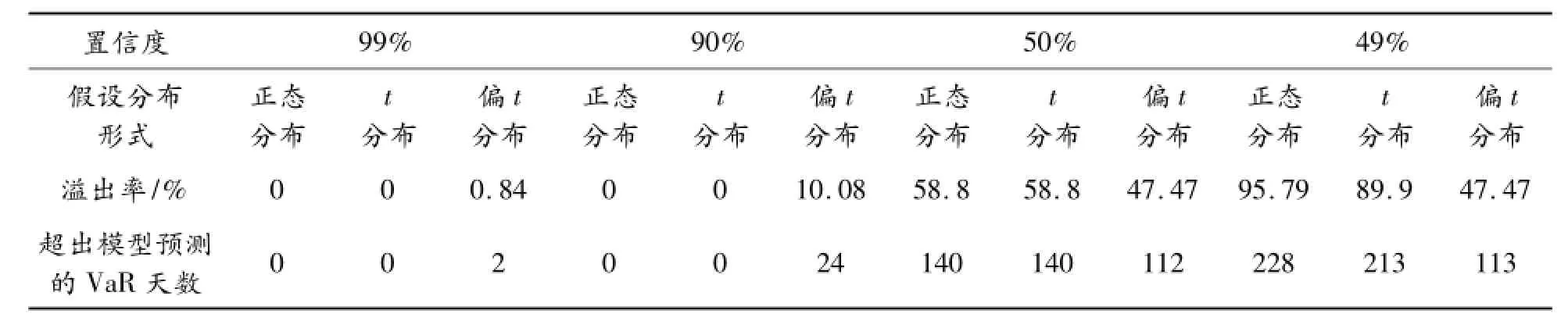
表2　基于不同分布假设下Realized GARCH（1，2）模型计算的VaR值的经验失败率

3　结束语

在风险值的计算中大都假定金融收益序列服从正态分布，但研究表明金融资产收益率序列的真实分布是厚尾的，而由于受到市场发展水平和参与者成熟程度以及对利空和利好信息的反应差异等诸多因素的影响，收益率序列往往也不是对称分布，而是呈现出不同程度的左偏和右偏。虽然t分布能够较好地描述收益率的厚尾特征，但t分布是对称分布时不能描述收益率分布的偏性。本文用偏t分布假设下的R-GARCH（1，2）模型计算VaR值，通过与正态分布和t分布假设下的RGARCH（1，2）模型的比较可以看出：偏t分布假设下的R-GARCH（1，2）模型对风险价值的测度优于正态分布和t分布假设下的R-GARCH（1，2）模型，表明基于偏t分布的R-GARCH（1，2）模型更加适合金融市场分析。

［1］Jorion P.Risk2：Measuring the Risk in Value at Risk［J］.Financial Analysts Journal，1996，52（6）：47-56.

［2］Ruey ST.Analysis of Financial Time Series［M］.Third Edition.Canada：Wiley-Interscience，2010.

［3］Engle R F.Autoregressive conditional heteroskedasticity with estimates of the variance of U.K.Inflation［J］. Econometrica，1982，50：987-1007.

［4］Bollerslev T.Generalized Autoregressive Conditional Heteroskedasticity［J］.Journal of Econometrics，1986，31：307-327.

［5］Bangzheng Zhang，Yu Wei，Jiang Yu，et al.Forecasting VaR and ESofstock index portfolio：A Vine copulamethod［J］.Statistical Mechanics and its Applications，2014，416：112-124.

［6］王理同，王晓叶，原俊青，等.基于半参数EGARCH模型的VaR和CVaR度量与实证研究［J］.数理统计与管理，2014，33（4）：655-659.

［7］赵晓玲，陈雪蓉，周勇.金融风暴中基于非参数估计的VaR和ES方法的风险度量［J］.数理统计与管理，2012，31（3）：381-388.

［8］Shephard N，Shepphard K.Realising the future：Forecasting with high frequency based volatility（HEAVY）models［J］.Journal of Applied Econometrics，2010，25：197-231.

［9］Hensen PR，Zhuo Huang，Shek H H.Realized GARCH：A jointmodel of returns and realized measures of volatility［J］.Journal of Applied Econometrics，2012，27：877-906.

［10］Fernandez CM S.On Bayesian Modeling of Fat Tails and Skewness［J］.Journal of the American Statistical Association，1998，441（93）：359-371.

［11］Visser M P.GARCH parameter estimation using high-frequency data［J］.Journal of Financial Econometrics，2011（9）：162-197.

［12］Augustyniak M.Maximum likelihood estimation of the Markov-switching GARCH model［J］.Computational Statistics&Data Analysis，2014，76：61-75.

（责任编辑刘舸）

M easurement of Risk Based on Realized GARCH（1，2）M odel w ith Different Residual

WEIZheng-yuan，ZHANG Xin，ZHAO Yu

（College of Mathematics and Statistics，C? hongqing University of Technology，Chongqing 400054，China）

We built the realized GARCH（1，2）modelwith skewed student's t distribution to forecast VaR of Shanghai Stock Exchange380 index for the high-frequency financial data with a fat tail and asymmetry.The model with normal distribution and student's t distribution was used for comparison. The empirical results show that the realized GARCH model with the skewed student's t distribution can identify the characteristics of the return series of Shanghai Stock Exchange 380 index and measure the risk of Shanghai Stock Exchange 380 indexmore accurately.

high-frequency data；realized GARCH；VaR；skewed student's t distribution；fat tail；asymmetry

O21

A

1674-8425（2015）05-0137-05

10.3969/j.issn.1674-8425（z）.2015.05.024

2015-02-10

重庆市自然科学基金资助项目（cstc2012jjA00018）；重庆市教委科学技术研究项目（KJ130810）；重庆市高等教育教学改革研究项目（1203053）

魏正元（1975—），男，博士，副教授，主要从事应用概率统计、金融统计、金融数学研究。

魏正元，张鑫，赵瑜.上证380高频指数数据已实现GARCH（1，2）模型的风险测量［J］.重庆理工大学学报：自然科学版，2015（5）：137-141.

format：WEIZheng-yuan，ZHANG Xin，ZHAO Yu.Measurement of Risk Based on Realized GARCH（1，2）Model with Different Residual［J］.Journal of Chongqing University of Technology：Natural Science，2015（5）：137 -141.