基于数据驱动的动车组齿轮箱在线故障预报*

王　锋， 张　兵， 林建辉

（西南交通大学牵引动力国家重点实验室 成都，610031）



基于数据驱动的动车组齿轮箱在线故障预报*

王锋， 张兵， 林建辉

（西南交通大学牵引动力国家重点实验室 成都，610031）

齿轮箱作为高速动车组的关键部件之一，其工作性能直接影响到高速动车组运行的可靠性和安全性。动车组齿轮箱结构复杂，且在实际运行中可能受到很多外界因素的激扰，难以建立合适的动力学模型。笔者介绍了一种检测高速动车组齿轮箱故障的时间序列算法，该方法基于数据驱动，不需要建立动力学模型，适合在线故障预报。无线微机电传感器从齿轮箱测得加速度信号并建立时间序列模型，利用模型的自回归参数定义故障敏感参数（FSP）。在有故障和无故障两种状态下，FSP均值完全不同。通过比较FSP均值，然后用假设检验中的t检验判定是否存在故障。实践证明，笔者提出的方法能较好地在线识别高速动车组齿轮箱早期故障，具有重要的应用意义。

时间序列；ARMA模型；故障敏感参数；t检验

引 言

随着列车运营速度的不断提升，高速列车的运行安全性和可靠性研究变得越发重要。作为高速动车组动力传递的关键部件，齿轮箱的任何细小故障都可能引发重大安全事故。为进一步完善高速动车组安全运营相关理论，急需开展对高速列车齿轮箱的故障预报研究。

当前齿轮箱的故障诊断方法很多，如振动诊断［1］、噪声分析［2］、扭振分析［3］、油液分析［4］、声发射［5］、温度［6］及能耗监测［7］等。高速动车组是一个非常复杂的非线性系统，其动力分散，具有大编组和高速化等特点。考虑高速动车组的实际运行特点，常见的动车组齿轮箱故障诊断，多是基于振动、温度和噪声的测试分析［8］。动车组齿轮箱结构复杂，且在实际运行过程中由于轮轨间的非线性耦合关系，可能受到各种外界因素的激扰，难以建立合适的动力学模型。而且，系统建模方法涉及有限元建模，系统辨识的计算过程复杂，无法实现在线故障预报。

为了解决上述问题，笔者提出了一种基于数据驱动的检测动车组齿轮箱故障的时间序列算法。该方法基于黑箱理论，不需要建立动力学模型，适合在线诊断及故障预报。在有限的安装空间，利用低功耗无线微机电传感器（micro electro-mechanism sensor，简称MEMS）组成密集的无线传感网络，MEMS从齿轮箱测得加速度信号并建立时间序列模型，通过无线网络回传模型的特征参数，利用特征参数来定义故障敏感参数（fault sensitive parameters，简称FSP）。在有故障和无故障两种状态下，FSP的均值完全不同。通过比较FSP均值，然后用假设检验中的t检验判定是否存在故障。通过决策层多传感器数据融合，判定齿轮箱故障状态。实践证明，笔者提出的方法可以较好地识别高速动车组齿轮箱早期故障，具有重要的实际应用意义。

1 试验方案及数据预处理概述

动车组整车试验系统由无线数据采集系统、列车级检测系统、地面数据处理系统、远程监控中心等4个子系统组成。图1为试验系统的组成结构图。

无线数据采集系统由传感器（振动、动应力、温度、压力等）、调理器、采集器和ZigBee网络组成，功能为采集测点的位移、加速度、应变、温度和压力等物理量，将采集信号存储在微型大容量的采集卡中，计算物理量的特征参数（均值、最大值、变化率、主频等）并将特征参数通过ZigBee无线网络传输到列车监测系统中。

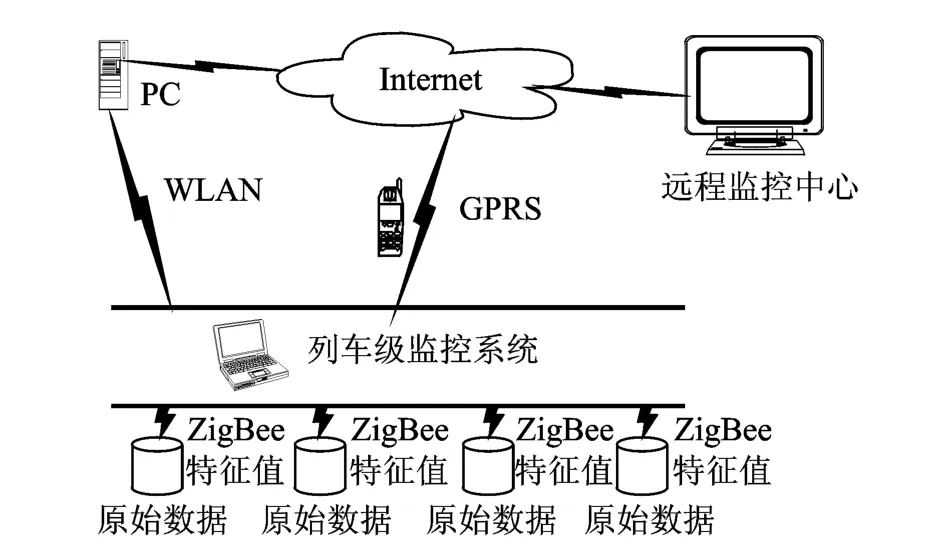
图1　跟踪试验系统的组成结构图Fig.1 Schematic diagram of sensor on gearbox

列车级检测系统主要由采集器、交换机、车载电脑、3G路由和GPS（测速模块）构成，车载电脑通过车内局域网对整个采集系统进行控制。

地面数据处理系统设在动车所或检修基地，由地面主机和无线接入器组成，负责入库后列车级监测系统的数据下载，对数据进行初步处理，为动车段提供数据异常信息等，便于进行检修。

远程监控中心利用GPRS网络实时传输过来的动车组高速运行时列车级监测系统的数据，远程时空同步监控动车组关键部件的工作状态，同时对数据进行综合分析处理，提供列车的状态特性，完成各种历史数据的对比分析。

远程监控中心利用GPRS网络，实时传输动车组高速运行时列车级监测系统的数据，远程时空同步监控动车关键部件的工作状态，同时对数据进行综合分析处理，提供列车的状态特性并完成各种历史数据对比分析。

图2给出了某列动车组跟踪试验中齿轮箱位置的传感器布置示意图。

图2　齿轮箱测点传感器布置示意图Fig.2 Schematic diagram of sensor on gearbox

为了实现不同类型数据的比较，保证模型的通用性，需要对传感器测得的原始数据进行预处理。数据预处理包括异点剔除［9］、趋势项消除［8］、归一化处理等。对于第i个传感器测得的信号xi（t），其归一化信号可由下式获得：

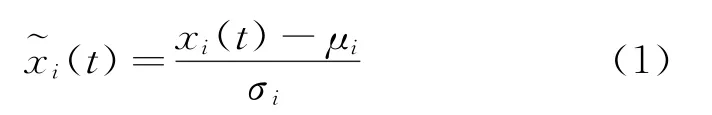
其中：μi和σi分别为xi（t）的均值和标准差。

2 故障预报原理

动车组实际运营过程中可能受到很多随机因素的影响，理论上讲，一列在平稳线路上正常行驶的动车组，其测得信号（加速度、温度等）应为随机时间序列。测得数据包含4个方面的信息：a.序列本身的结构与规律，或者说，相应系统的行为特性；b.相应系统本身的固有属性（即系统的结构与参数），这一固有属性同外界作用无关；c.外界对系统的输入；d.相应系统同外界联系的方式，即外界以什么方式对系统施加输入。

动车组齿轮箱在故障前期的初始表现往往是振动异常，因为故障会影响齿轮箱的结构动态特性，导致测得的振动加速度信号的统计特性随时间历程而改变。因此，可以通过时间序列分析故障前后测得的加速度信号，识别齿轮箱早期故障（包括电蚀、齿面磨损、齿面剥落、齿根裂纹以及箱体疲劳等）。当设备状况持续恶化过程中，可用不同的探测技术监测动车组齿轮箱的运行状态。

动车组齿轮箱整个生命周期的状态监测方法如图3所示。

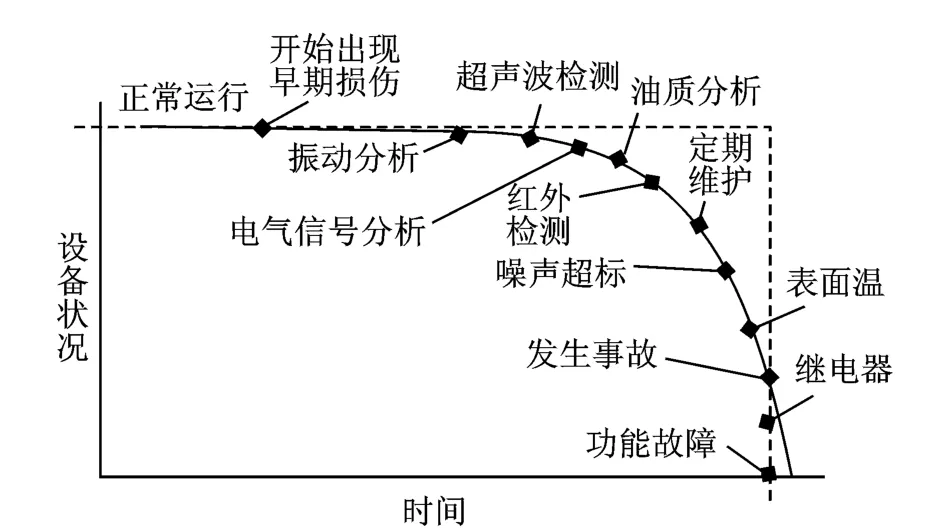
图3　动车组齿轮箱状态监测方法Fig.3 The condition monitoring method of the gearbox

3 故障预报算法

3.1时间序列建模

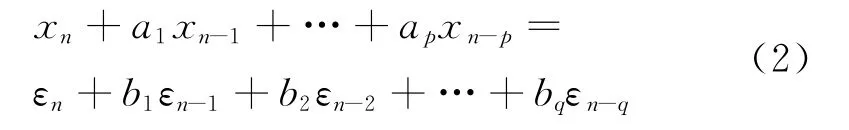
数据预处理完成后，可以用来进行时序建模。一个ARMA（p，q）过程的一般形式［10］为其中：ap为自回归系数；bq为滑动平均系数；εn为白噪声激励，εn的均值为0，方差为σ2ε。

当q=0时，式（2）表示一个纯自回归模型，记为AR（p）；当p=0时，式（2）表示一个纯滑动平均模型，记为MA（q）。一个有连续谱密度函数的平稳随机过程，可以表示为一个确定AR（∞）或MA（∞）随机过程。时序建模的过程即确定模型阶次p，q和模型参数ap，bq的过程。

建立准确的时间序列模型，是正确预报故障的关键。通过选择合适的判定函数以及比较不同类型时序模型之间的预测误差［11-12］，可以实现数据的自适应时序建模［13］，自动选择最佳的模型类型（AR模型、MA模型或ARMA模型），并确定模型的最佳阶次。自适应时序建模流程图如图4所示。

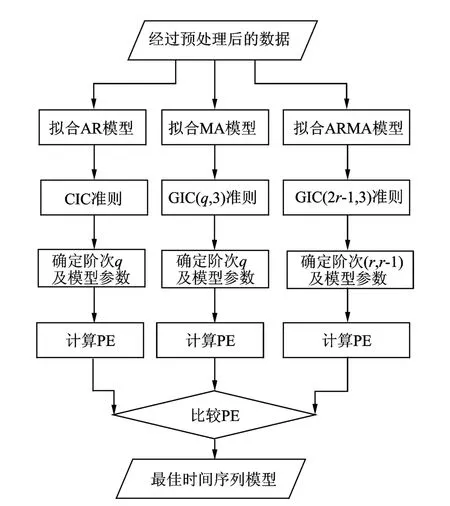
图4　算法流程图Fig.4 Flowchart of the algorithm

分别根据CIC准则选择最优的AR（p）模型、根据GIC（q，3）准则选择最优的MA（q）模型、根据GIC（2r-1，3）准则选择最优的ARMA（r，r-1）模型后，3个模型的预测误差可以通过给定时序进行估计。MA模型和ARMA模型的预测误差为

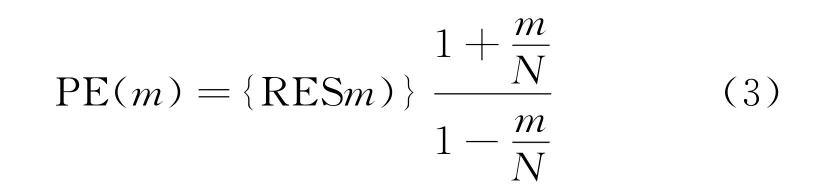
其中：m为模型中的参数个数，RES（m）为模型残差。

对于AR（p）模型，其预测误差为

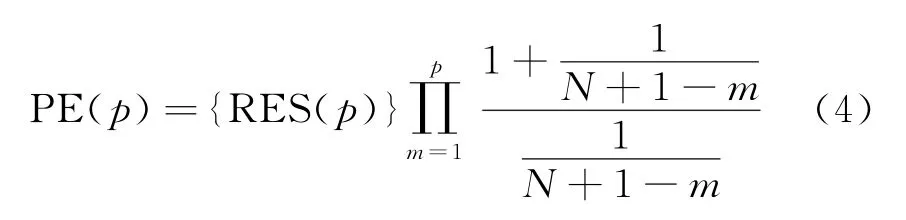
在估计参数数量大于N/10时，式（4）得出的结果与式（3）有显著差异。通过比较两式的结果，可以自动识别预测误差最小的模型，实现了自适应建模的目的。

3.2ARMA模型参数敏感性分析

时间序列模型的AR系数中包含关于系统模态固有频率和阻尼比的信息。在有输入信号（假设为白噪声）时，ARMA模型可被视为带外源输入时序（ARX）的自回归模型，该模型可用z变换的时移特性在复数z域检查。

关于∂α2/∂θi和∂α3/∂θi的关系推导与此相同。

由上可得，当齿轮箱发生故障时，必然会导致其刚度变化，同时带来其响应的改变和基于响应建立的时序模型AR系数的改变。因此，基于AR系数的FSP参数可以测得这种变化并预报齿轮箱故障。

3.3故障敏感参数（FSP）

根据上面得到的最佳时序模型，可有效识别齿轮箱特征参数。经过自适应建模的时序模型，其AR参数表征动车组齿轮箱的固有特性，MA参数表征外界随机激励。当发生故障时，部分特征参数会发生改变。但并非所有特征参数都对故障敏感，将在有故障和无故障两种状态下存在显著差异的时间序列模型特征参数或其组合定义为故障敏感参数（FSP）。

选取FSP的基本原则：a.独立性：对速度等频繁变化的外界因素不敏感；b.相容性：最好是无量纲量，方便不同传感器数据融合；c.稳定性：同一状态下不应该发生剧烈改变，满足正态分布特征，其变动范围以不超过全局极大值和极小值差值的一半为宜；d.完备性：在有故障和无故障两种状态下，FSP值应该发生显著变化。

在对比动车组齿轮箱加速度历史数据并计算几组不同的FSP之后发现，对动车组齿轮箱早期故障而言，时序ARMA模型的前3阶AR系数的统计意义最为显著。由此定义早期故障的FSP为

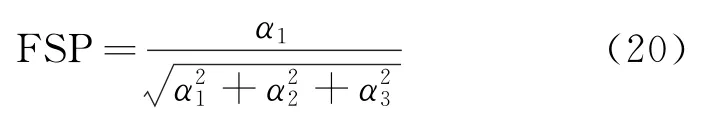
其中：α1，α2，α3分别为时序模型的前3个AR系数。

3.4故障判定方法

直接采信被观测对象功能及性能信息的特征参数改变进行故障诊断，是置信度最高的故障诊断方法。但是，除了故障诊断算法本身的设计问题外，由于车上与实验室工作应力和环境应力的不同，使得车上测试状态与地面复测状态存在差异，可能导致虚警率较高［13-14］。由此引入假设检验方法，提高故障判定的准确率。

用μFSPd和μFSPu分别代表有故障和无故障两种状态下FSP参数的均值，建立如下假设：

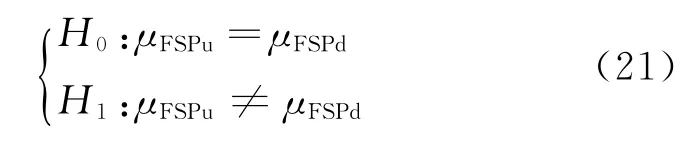
其中：H0和H1分别为无效假设和备选假设。H0代表无故障状态，H1代表故障状态。显著性水平设为0.05。

4 动车组齿轮箱故障预报实例分析

在跟踪试验中，为了监控齿轮箱的运行状态，在齿轮箱上部和下部均安装了三向加速度传感器，测试相对列车行进方向的横向、纵向和垂向加速度，采样频率为2 k Hz。下面以动车组齿轮箱早期故障为例，说明故障预报的过程。

随意截取某次试验某个测点在不同速度下的5段数据进行分析（编号为xi，i=1，2，3，4，5），每段数据的长度为4 000点（采样时间2 s）。首先对这5段数据进行异点剔除、趋势项消除和归一化预处理，预处理后的加速度数据如图5所示。

接下来对这些数据进行自适应建模分析，并检验模型的适用性，判断模型的稳定性。实际应用过程中，最为关键的是选取合适的时序模型及其阶次，同时确定最佳的分析点数。将每段数据分为j个长度为n的子段（编号为xij，其中i=1～5，j=1～4 000/n），对每个xij进行自适应建模。按照同样的方法建立所有子段的模型后，分析模型前三阶AR系数的均值和方差，依此判断模型是否稳定，从而得到最佳的建模数据点数。对其中一段数据分析的结果如表1所示（μαi表示特征参数αl的均值，σαl表示特征参数αl的方差，l=1，2，3），其余4段的分析过程与此相同。

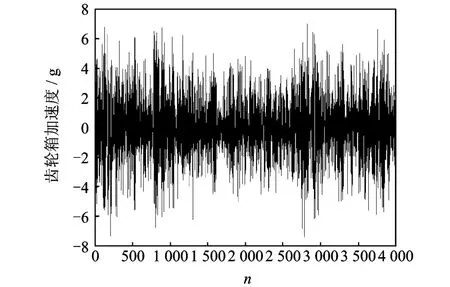
图5　经过预处理后的加速度数据Fig.5 The acceleration data after preprocessing

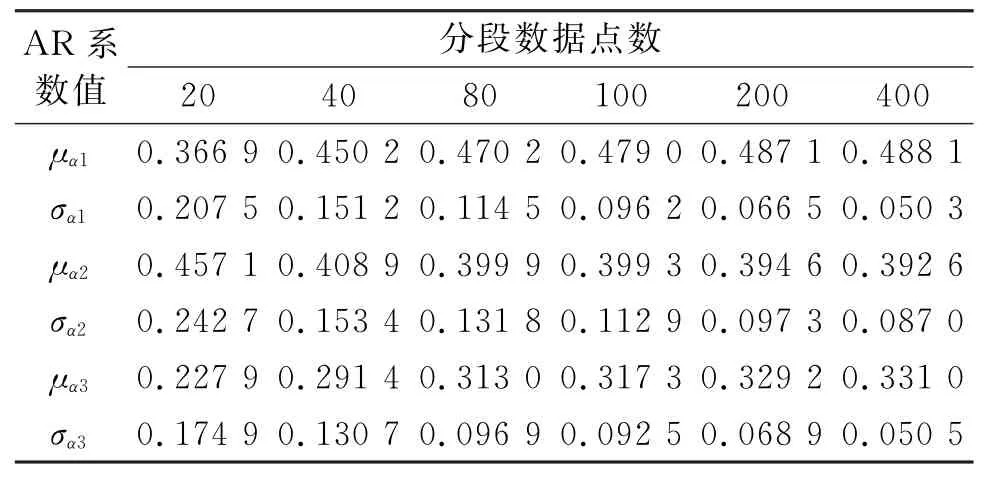
表1　AR系数相对于数据点数量的敏感性Tab.1 Sensitivity of AR coefficients to the number of data points

从表1可以看出，前3阶AR系数在100点时基本稳定。为了在模型稳定性和故障预报实时性之间取得平衡，实际计算时取200点分段长度的子段进行分析。随意选取其中一个长度为200点的子段进行自适应建模如图6所示。从图6可以看出，估计误差最小的适用模型为AR（15），与自适应建模算法得出的结果一致。在确定模型稳定且对故障敏感的数据长度后，对每一小段的数据进行自适应建模并计算FSP值，结果如图7所示。从图中可以看出，5段数据FSP的均值发生了明显变化。如果第1，2段数据处于正常状态，那么第3，4，5段数据所在时间点出现齿轮箱状态异常的概率很大。为了提高故障预报的准确率，用t检验判断故障状态。计算结果为0.001 4，即在置信度为99.86的范围内，接受两者均值不同的假设。即从第3段数据所在时间点开始，存在齿轮箱出现早期故障的可能。

对所有传感器用相同方法计算FSP并作t检验，然后将计算结果进行决策层数据融合之后可以判定：从第3段数据所在时间点开始，齿轮箱出现早期故障。与停车检修记录相符，证明了所述方法的有效性。

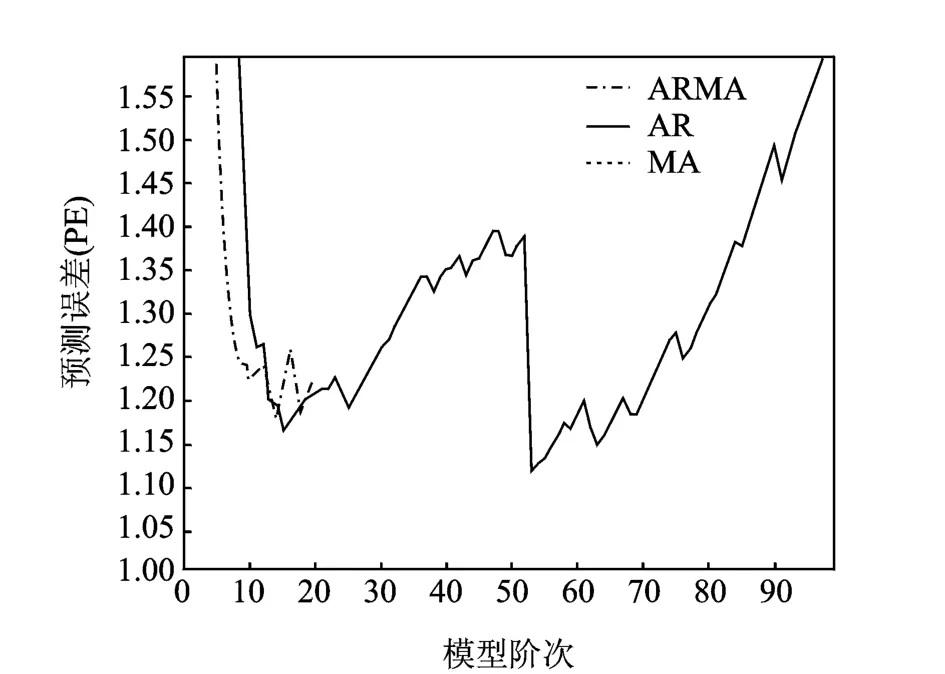
图6　估计准确率与模型类型和阶次的关系Fig.6 Estimated model accuracy as a function of the model type

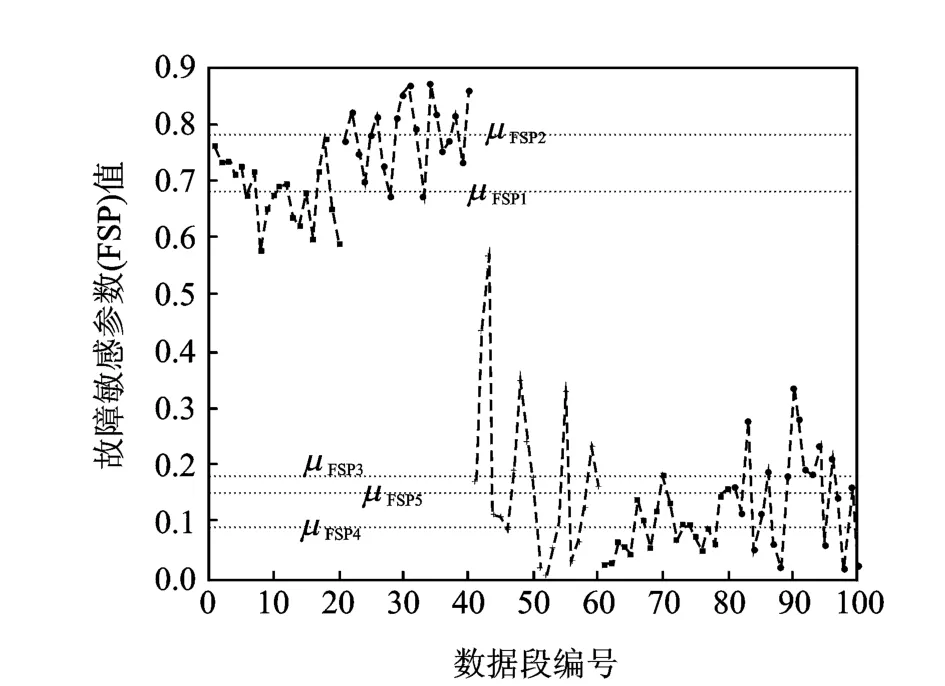
图7　不同数据段的FSP值Fig.7 Estimated model accuracy as a function of the model type

5 结束语

笔者提出了一种基于数据驱动的动车组齿轮箱故障预报方法。该方法模型简单，可以有效识别齿轮箱早期故障，适用于动车组齿轮箱在线故障预报，具有重要的实际应用意义。

［1］ 田涛，丁康.希尔伯特变换及其在故障诊断中的应用［J］.振动与冲击，1996，15（2）：24-27，14，102. Tian Tao，Ding Kang.Hilbert transform and its application in the failure diagnosis［J］.Journal of Vibration and Shock，1996，15（2）：24-27，14，102.（in Chinese）

［2］ 任明章，连小珉，蒋孝煜，等.齿轮箱噪声故障诊断专家系统的研究与开发［J］.清华大学学报：自然科学版，1996，36（8）：66-71. Ren Mingzhang，Lian Xiaomin，Jiang Xiaoyu，et al. Research and development of a diagnostic expert system for gearbox noise［J］.Journal of Tsinghua University：Sci&Tech，1996，36（8）：66-71.（in Chinese）

［3］ 樊可清，屈梁生.基于扭振信号的齿轮故障诊断研究［J］.中国机械工程，1999，10（4）：430-433. Fan Keqing，Qu Liangsheng.Diagnosing gears defect with torsional vibration signal［J］.China Mechanical Engineering，1999，10（4）：430-433.（in Chinese）

［4］ 李臻，荆双喜，冷军发，等.油液分析技术在齿轮减速箱故障诊断中的应用［J］.煤矿机电，2003，27（3）：27-29. Li Zhen，Jing Shuangxi，Leng Junfa，et al.The Application of oil analytic technique in fault diagnosis of gearbox［J］.Colliery Mechanical&Electrical Technology，2003，27（3）：27-29.（in Chinese）

［5］ 于洋，赵年伟，杨平，等.齿轮磨损故障声发射检测研究［J］.机械传动，2013，37（4）：44-48. Yu Yang，Zhao Nianwei，Yang Ping，et al.Research on the gear wear failure based on Acoustic emission detection［J］.Journal of Mechanical Transmission，2013，37（4）：44-48.（in Chinese）

［6］ 屈文涛，沈允文，徐建宁，等.双圆弧齿轮传动的温度场和热变形分析［J］.石油机械，2006，34（3）：13-15，19. Qu Wentao，Shen Yunwen，Xu Jianning，et al.Analysis on temperature tield and thermal deformation of double-arc gear drive［J］.China Petroleum Machinery，2006，34（3）：13-15，19.（in Chinese）

［7］ 谢小鹏，冯伟，黄敦烈，等.基于能量耗损的摩擦学系统状态识别方法研究［J］.润滑与密封，2010，35（2）：27-31. Xie Xiaopeng，Feng Wei，Huang Dunlie，et al.Study on state recognition method of tribological system based on energy loss［J］.Lubrication Engineering，2010，35（2）：27-31.（in Chinese）

［8］ 丁福焰，杜永平.机车车辆故障诊断技术的发展［J］.铁道机车车辆，2004，24（4）：24-29. Ding Fuyan，Du Yongping.Development of fault diagnosis technology for locomotive and car［J］.Railway Locomotive&CAR，2004，24（4）：24-29.（in Chinese）

［9］ 段虎明，谢飞，张开斌，等.海量道路路面测量数据的若干预处理方法研究［J］.振动与冲击，2011，30（8）：101-106，117. Duan Huming，Xie Fei，Zhang Kaibin，et al.Methods of signal pre-processing with massive road surface measurement data［J］.Journal of Vibration and Shock，2011，30（8）：101-106，117.（in Chinese）

［10］Priestley M B.Spectral analysis and time series［M］. New York：Academic，1981.

［11］Broersen P M T.Selection of type and order of time series models［C］∥Proceedings of the 38th IEEE Conference.Phoenix，AZ：IEEE，1999，5：5064-5069.［12］Broersen P M T.Finite sample criteria for autoregressive order selection［J］.IEEE Trans Signal Processing，2000，48：3550-3558.

［13］Broersen P M T.Facts and fiction in spectral analysis［J］.IEEE Transactions on Instrumentation and Measurement.2000，49：766-772.

［14］曾声奎，Pecht M G，吴际，等.故障预测与健康管理（PH M）技术的现状与发展［J］.航空学报，2005，26（5）：626-632. Zeng Shengkui，Pecht M G，Wu Ji，et al.Status and pers pectives of prognostics and health management Technologies［J］.Acta Aeronautica Et Astronautica Sinica，2005，26（5）：626-632.（in Chinese）

TH17；U298.1

10.16450/j.cnki.issn.1004-6801.2015.02.005

王锋，男，1979年10月生，博士生，助理研究员。主要研究方向为铁路机车车辆设计安全检测技术和试验研究、信号分析与处理。曾发表《基于光纤陀螺的高速列车轨迹无线测试仪》（《计算机测量与控制》2012年第20卷第11期）等论文。

E-mail：wf@xnjd.com.cn

*“十一五”国家科技支撑计划资助项目（2009BAG12A01-E03）、四川省科技厅资助项目（2011S20007）、高等学校博士学科点专项科研基金资助项目（2012G04005）

2013-11-25；

2014-11-30