基于RF-GLR组合机器学习算法的防空体系能力指标挖掘方法研究
姚晓毅 郭圣明 胡晓峰 杨镜宇
1.国防大学信息作战与指挥训练教研部北京100091
1 问题的提出
现代信息化战争中,防空体系是集侦察预警、火力拦截、指挥控制、网络通信、电磁对抗等系统于一体的复杂体系,其各组分系统之间交互频繁复杂,具有典型的复杂性特征.而防空作战体系能力是体系在完成使命任务的对抗过程中通过组分系统间的动态交互涌现出来的,并随着体系演化不断发展变化.因此,从体系的复杂性入手,将体系非线性、不确定性、自适应性、涌现性等的复杂性质反映在体系能力评估中,已成为体系作战研究领域的共识,而如何选取构建反映防空作战体系“整体、动态、对抗”特点的体系指标成为体系能力评估的关键问题和主要挑战.目前,防空体系能力评估研究中,体系能力指标大多采用基于专家经验的树状指标选取方法,即以防空领域专家的知识和经验为依据制定指标,在专家打分的基础上,采用模糊数学模型、指数法模型或ADC方程模型等方法对体系能力评估[1−4].此类方法虽然在一定程度上反映了体系整体性特点,但更多反映的是体系静态能力,无法描述体系动态交互过程中涌现的体系能力及能力指标之间的关联关系,且专家主观因素占较大比例,不能满足信息化条件下防空作战的全面、客观、实时的体系能力评估要求.
防空体系作战仿真实验和数据挖掘技术的结合为解决防空复杂体系能力指标的选取提供了可行的途径.防空体系仿真实验通过分析记录的防空体系作战多视角、全维度元数据,描述作战实体自适应行为涌现出的体系行为规律;而数据挖掘的方法强调从仿真实验得到的元数据入手,将隐没数据中的重要信息提炼出来,把具有错综复杂关系的大量分系统基础指标综合成少量能够描述体系能力的指标,在不失去主要信息的前提下简明扼要地把握体系的本质特征,为研究不确定条件下战争复杂系统的评估问题提供了一种新的思路[5−10].
本文以复杂条件下的防空体系作战为想定背景,以要点目标防护为使命任务,以武器装备体系仿真实验床中平台仿真实验运行的基础数据为样本数据,采用机器学习方法挖掘出防空体系作战能力指标——重要目标的防空威胁指数,较好地实现了对体系能力的实时评估和预测,为指挥员提供实时、准确、客观的决策依据.
2 基于武器装备体系仿真实验床的防空体系作战仿真实验设计
传统单方、静止、确定的实验方法获取的数据展现不出防空体系能力的整体涌现性、动态性和进化性,而武器装备体系仿真试验床是一种新型的武器装备体系研究方法,强调在动态对抗中研究武器装备体系,采取多维比对等方法展现武器装备体系内部各组分之间多网联动而产生的自组织、自适应、涌现、坍塌和不确定等复杂现象.因此,本文针对研究的防空体系作战能力问题,利用武器装备体系仿真试验床设计构建“整体、动态、对抗”的防空体系仿真实验,并通过不断改变实验因子收集防空体系作战中完整、实时、对抗的全息样本数据,为体系能力指标挖掘提供数据基础.
2.1 防空体系实验背景想定设计
想定设计的防空作战任务为重要目标防护.具体背景:蓝方空袭机群突然发动对红方的空袭行动,空袭目标设置为红方重要中心指挥所;红方预警机探测到威胁目标后,指挥临近巡逻的战斗机进行拦截,调派远方战斗机前来支援作战,并将情报信息传给地面和海上指挥所,各级指挥所指挥舰艇防空导弹和地面地空导弹在导弹射程内发射防空导弹拦截蓝方空袭机群;蓝方侦察机首先对红方目标进行侦查,将情报传递给空袭机群,蓝空袭机群中电子战飞机对红方装备实时进行电磁压制,战斗机群与红方防空体系发生交战,歼灭红方空中战斗机、海上舰艇、地面地空导弹,突破红方的空中、海上、地面3层防空网,最后摧毁红方重要中心指挥所,达成空袭作战目标.
实验中,通过不断变换蓝方空袭机群飞机的数量、速度、高度、密度、雷达识别特征、突入方向、空空导弹和空地导弹的发射距离、指挥通信协同网络、预警机指挥、电子战机电磁干扰等实验参数来提高蓝方空袭的强度,激励红方防空体系的自适应行为和涌现性能力,多角度、全维度收集红方防空体系作战数据,如图1所示.
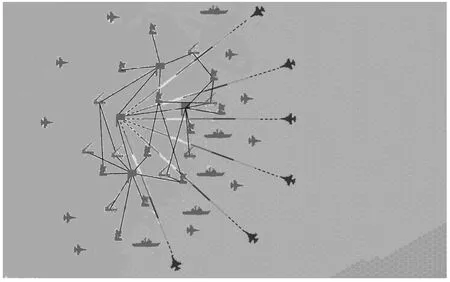
图1 防空体系作战简化示意图
2.2 采集的实验数据真实描述“整体、动态、对抗”的防空体系作战
多角度、全维度的运行数据反映体系的整体性:红方防空体系中的防空装备按照指挥通信关系与背景体系的其他装备通过指挥网、传感网、通信网互联.通过与背景体系的互联互通来获得防空体系的完整数据,能够反映出防空体系的整体性.
实时运行数据反映体系的动态性:各类装备平台通过指挥通信网络对目标信息实时探测、处理融合与共享,实时传输指令进行防空作战.通过对防空体系的动态设置,获得防空体系按照一定的时间步长实时输出的动态数据,反映出各类武器装备的动态交互关系和交互过程.
红蓝交战数据反映体系的对抗性:通过红方防空体系与蓝方空袭机群的体系对抗,并改变蓝方空袭机群的参数设置来提高对抗强度,获得的红方防空体系交互数据能够显现出体系的涌现性和自适应性等复杂特性.
2.3 防空体系仿真能力指标涌现框架
防空作战体系能力通过组分系统之间的复杂交互涌现出来,因此,作为评估体系能力的体系指标应该是体系组分系统基础指标参数的“涌现和”.红方防空体系对抗蓝方空袭机群的仿真实验中,防空武器装备体系生成的海量元数据以各个分系统基础指标参数的形式记录下来,基础指标参数大体可分为侦察预警类数据(如防空体系探测识别敌机数量、距离时间等)、情报处理类数据(如防空体系的情报收集、处理、分发时间等)、火力交战类数据(如防空体系地面、海上、空中战损装备数量、拦截敌机数量等),电磁对抗类数据(如防空体系受干扰各类装备数量及性能变化等)和通信类数据(如防空体系通信网数量、通信量等)等.而防空作战的体系能力最终通过基础指标参数的聚合涌现出的体系能力指标来描述,其结构框架如图2所示.
3 面向防空体系作战能力指标构建的机器学习分析方法
机器学习方法通过对复杂数据的学习,训练相关模型,抽取体系整体特征并进行分类,以此来度量体系能力,随机森林和逻辑回归是其中典型的两种算法.随机森林算法[11−16]对样本数据容忍度高,泛化能力强,能够在有效回避过拟合同时有效处理多自变量的有限样本数据,得到针对某个具体问题的关键基础变量集.然而由于随机森林方法算法实现中每棵决策树分类依据往往是某一个变量,在整个体系特征分类和评估过程中实际是一个黑箱或灰箱操作,难以对得到的体系分类特征进行解释,所以需要在随机森林的基础上引入广义线性回归的方法,构建随机森林-逻辑回归组合分析模型.组合分析模型首先采用随机森林模型选择影响体系特征的重要基础指标参数,降低逻辑回归模型输入参数间的相关性对体系指标挖掘的影响,而后采用逻辑回归模型对重要基础指标参数二次回归,得到最优回归系数的同时,实现对体系能力指标的聚合涌现,同时得出组分系统参数对体系指标的贡献度.
3.1 基于随机森林算法的基础参数指标重要性分析模型
随机森林模型是一种组合分类器,利用多棵决策树对防空体系作战中重要目标是否会被摧毁进行分类训练和预测.构建每棵决策树时在节点使用随机抽取的部分基础指标作为分裂依据,并让每棵决策树尽可能生长而不修剪.在训练过程中,依据划分的基础指标参量对分类误差的影响来判断基础指标参数对体系的重要性.采用精度的平均递减(OOB误分率的增加量)和均方误差的平均递减(节点分裂产生的残差平方和均值)筛选出对防空体系的生存能力有重要影响的基础指标参数.
防空体系使命任务完成情况作为输出值y,用数值0表示要点目标未被摧毁,数值1表示要点目标被摧毁,基础指标参数向量x=(x1,x2,···xM)作为随机森林回归模型输入参数,构建模型训练样本集D={(x,y)}.防空体系生存能力的随机森林回归模型的算法如下:
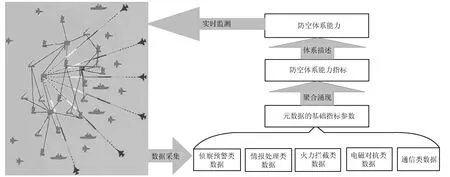
图2 要点防护能力指标评估框架
算法1:防空体系生存能力的随机森林回归模型算法
输入:D:防空体系基础指标参数组成的训练样本数据集{(x,y)}
M:输入的D中防空基础指标参数x(特征变量)的个数
k:独立重复抽取样本的次数(每次抽取获得的样本产生一棵决策树)
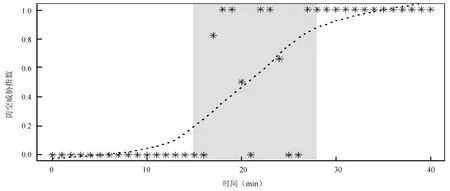
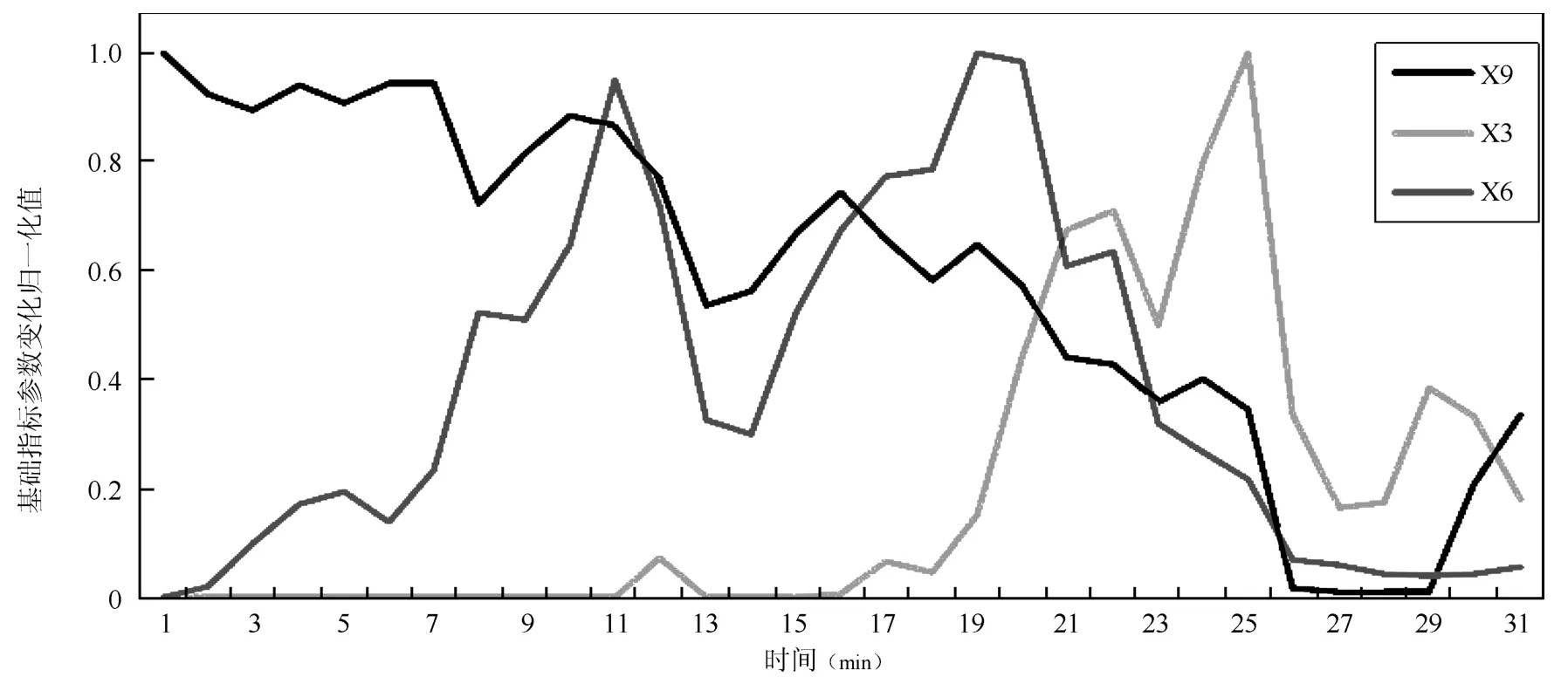
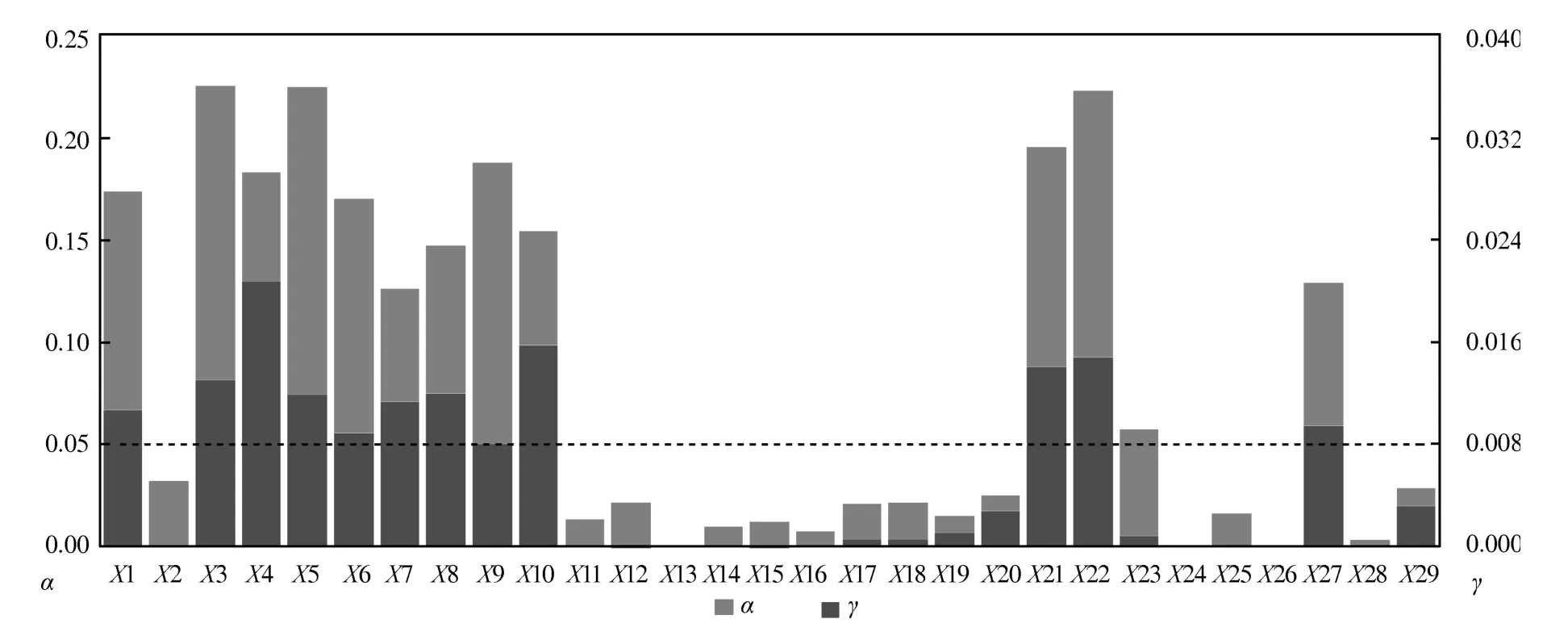
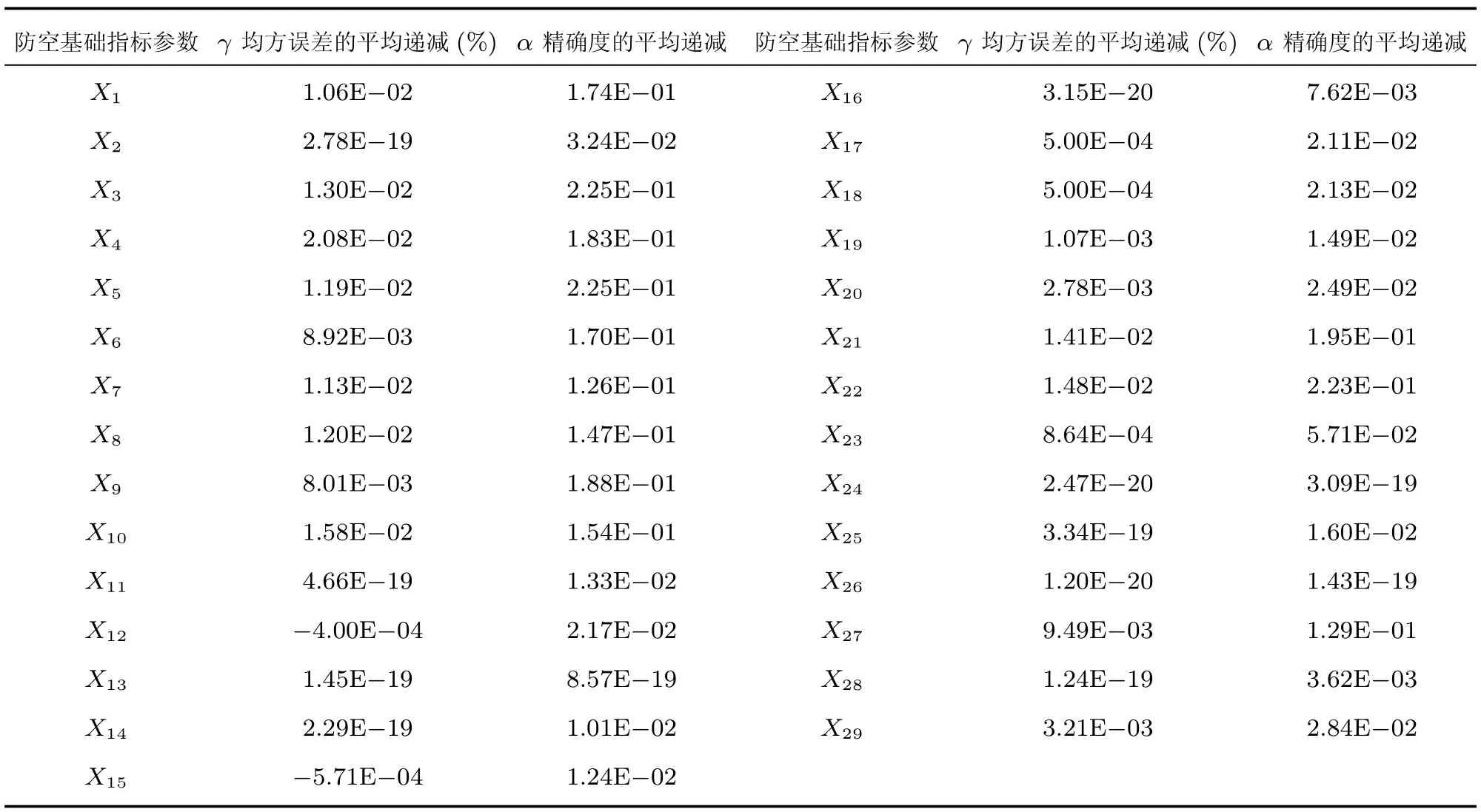
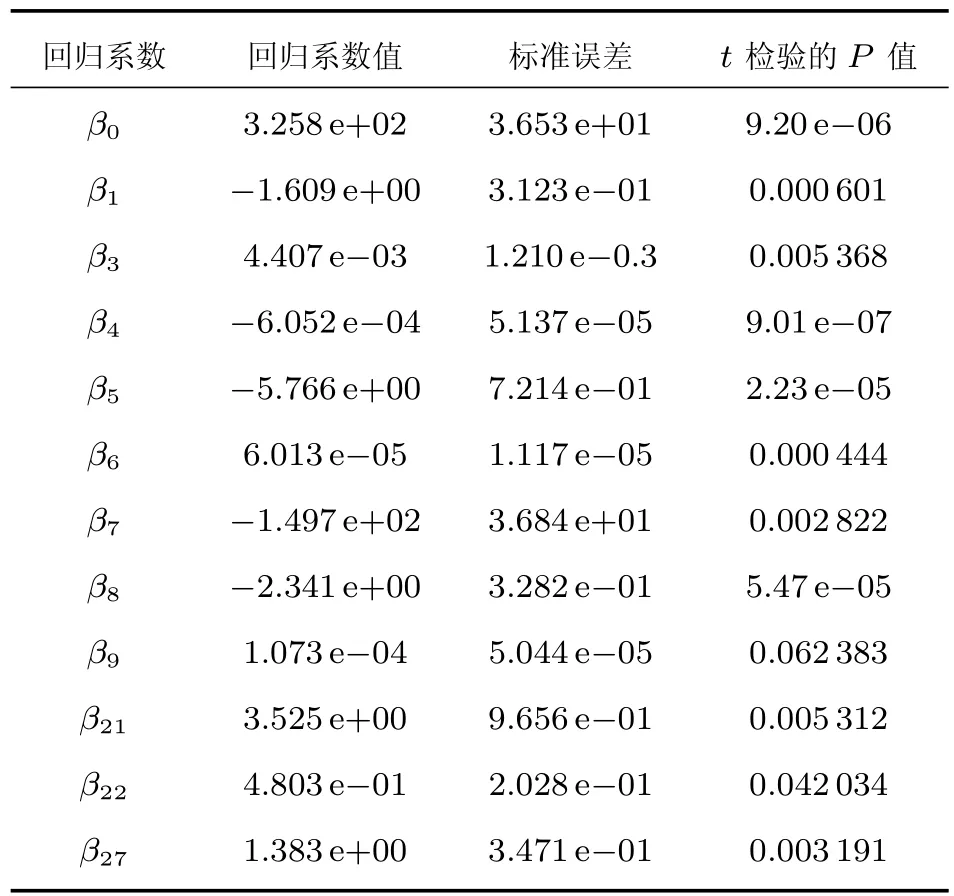
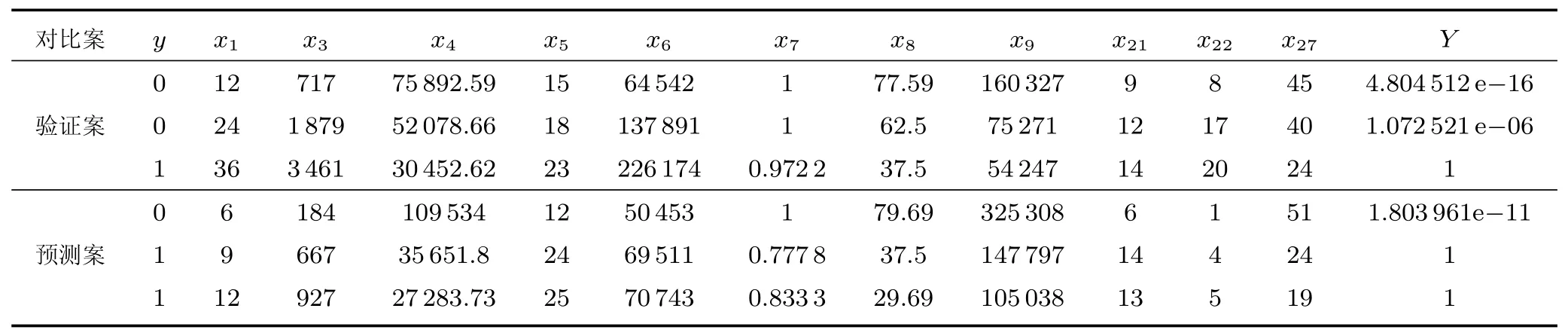
m:每次节点拆分时选择用于拆分的备选基础指标参数(特征变量)个数(m 输出:{h(x,Θk),k=1,···}: 防空体系生存能力的随机森林回归模型,αj,j=1,2,···,M:各防空基础指标参数的精度平均递减,γj,j=1,2,···,M:各防空基础指标参数的均方差平均递减 算法:#第1步训练出防空体系生存能力的随机森林回归模型. ①Fori=1 tokdo ②从D中有放回的随机抽取(bootstrap方法)形成样本Θi,剩余的数据为袋外数据样本OOBi. ③样本Θi单独构建一棵树hΘi:每棵树节点分裂时首先随机选取m个备选防空基础指标参数(特征变量),然后计算每个防空基础指标参数的残差平方和SSk(xj),根据残差平方和最小的原则,选择出最优的一个防空基础指标参数作为分裂变量进行拆分(CART方法): ④END ⑤组合k个分类树hΘ1,hΘ2,···,hΘk构成防空体系生存能力的随机森林回归模型{h(x,Θk),k=1,···},形成k个防空基础指标参数子集{Θ1,Θ2,···,Θk}, 剩余的数据形成袋外数据集{OOB1,OOB2,···,OOBk},每棵回归树预测值的加权平均为防空体系生存能力的随机森林回归模型的输出值Y. #第2步计算出防空基础指标参数的OOB误分率的增加量和节点分裂的残差平方和均值,以此度量基础指标参数对防空体系能力指标的重要性. ⑥运用防空体系随机森林回归模型对袋外数据{OOB1,OOB2,···,OOBk}进行预测得到 OOB的误分率W. ⑦将基础指标参数xj的数值在k个OOB样本中的顺序随机改变,形成新的OOB测试样本,然后用建立的随机森林模型对新的OOB进行分类,得到新的OOB误分率为Wj,标准化后得到每个变量的重要性度量αj: ⑧基础指标参数xj在{Θ1,Θ2,···,Θk}中节点分裂的残差平方和均值为γj: ⑨根据αj、γj的数值大小,共同筛选出重要的基础指标参数xj. 广义线性回归模型是能够处理防空体系生存能力的多元回归模型[17−18],形成的防空体系指标和各基础指标参数之间的关系式便于对防空体系指标的解释和直观显示.通过防空体系基础指标样本数据拟合出防空体系生存能力的广义线性回归模型,解释若干个防空体系基础数据变量x与防空体系生存指标y的取值关系,反映y与x之间的依存关系,属概率型非线性回归.设经随机森林模型筛选出的对防空体系生存能力有重要影响的n个变量为{x1,x2,···,xn},则描述防空体系生存能力的广义线性回归模型为: 广义线性回归模型算法采用最大似然估计来学习,通过最大似然估计的多次迭代推导出各基础指标参数的回归参数β0···βn的值,在迭代中采用梯度下降法使损失函数的值最小,迭代停止条件为算法达到某个可以允许的误差范围.并通过对各基础指标参数的t检验,检验其在数据样本中差异显著性,进一步筛选重要防空基础指标参数,提高获取的防空体系生存能力的广义线性回归模型质量.具体算法如下: 算法2:防空体系生存能力的广义线性回归模型算法 输入:D:随机森林筛选出的重要防空基础指标参数集{x1,x2,···,xn,y} 输出:P(y|x1,x2,···,xn):防空体系生存能力的广义线性回归模型,βj(j=0···n):各防空基础指标参数的回归系数β0···βn的值 算法: ①构建防空体系生存能力的预测函数hβ(x): ②对防空体系生存能力的预测函数取似然函数L(β): ③取对数似然函数l(β),最大似然估计是求使l(β)取最大值时的β值: ④采用梯度下降法求取损失函数J(β)的最小值,求得防空体系生存能力广义线性回归模型中的基础指标最佳回归参数βj: ⑤通过t检验衡量防空基础指标参数的差异显著性,进一步筛选基础指标参数,提高模型质量: ˆβ为Fisher得分迭代法对回归系数的估计,ˆωj为期望信息矩阵[τ(ˆβ)]−1的逆的第j个对角元素 ⑥获得能够反映防空体系生存能力的广义线性回归模型: 综上所述,可以定义P(y|x1,x2,···,xn)为度量防空体系作战能力的新指标——重要目标的防空威胁指数P,通过式(1)可以看出,P可以看作是防空体系重要基础指标参数的“涌现和”,反映了组分系统复杂交互以后形成的体系作战能力,同时逻辑回归的概率模型体现了防空体系作战的不确定性等特点. 在“整体、对抗、动态”的防空体系基本案仿真实验中获得了29项防空基础指标参数,用{x1,x2,···x29}表示,用y表示防空体系重要的中心指挥所是否被摧毁.防空体系生存能力的随机森林模型在处理防空体系仿真实验数据集时,作为重要基础指标参数筛选的过滤器,能够找出影响防空体系效能的关键基础指标参数项.随机森林模型对防空体系基本案仿真数据中各项防空基础指标参数的重要性度量值见表2和图3. 图3 随机森林对基础指标参数重要性度量图 表2 防空基础指标参数的重要性度量值 依据随机森林模型算法,精确度的平均递减 (αj)和均方误差的平均递减 (γj)可以作为衡量基础指标参数重要性的依据,基础指标参数的αj和γj的值越大,表明此基础指标与其他指标之间的相关性越小,也就是基础指标参数的显著性越强.依据表2的模型输出结果,按照 (αj>0.05&γj>0.008)的标准,筛选出对体系指标影响较大的防空基础指标参数为:x1、x3、x4、x5、x6、x7、x8、x9、x10、x21、x22、x27.这12项防空基础指标参数在均方误差的平均递减中所占比重>95%,在精确度的平均递减中所占比重>90%,说明它们是影响防空体系生存能力的主要基础指标参数. 通过防空体系生存能力的随机森林模型从29个防空基础指标参数中筛选出12个关键基础指标参数,降低了挖掘防空体系能力指标的复杂性. 将重要基础指标参数集作为逻辑回归模型的输入进行二次回归计算,并通过t检验对回归系数进行修正和校验,得出基础指标参数对防空体系能力指标的贡献度.其中t检验结果表明,x10对应的P值大于0.1,说明x10在基础指标参数集中的差异显著性不强,进一步删除x10后得到修正的防空基础指标参数的回归系数和误差结果如表3所示. 表3 防空体系Logistic回归模型输出表 依据式(1)得出防空体系中重要目标的防空威胁指数P为: 防空体系中重要目标的防空威胁指数P是描述防空体系中的重要防护目标受到敌空中威胁的变化程度,反映了防空体系遭到敌空袭机群突防时的防空能力变化情况,它不是静态的一个数值而是随防空作战进程或者敌空袭强度的变化而不断变化的.当重要目标的防空威胁指数P为1时,表明防空体系的防空能力达到饱和,预示重要防护目标可能即将被敌摧毁.获得的防空体系重要目标的防空威胁指数P是关键防空基础指标参数xj的“涌现和”,反映了组分系统复杂交互以后的防空体系作战能力,同时体现出了防空体系作战的不确定性等特点. 把防空体系的基础指标参数做归一化处理,然后经防空体系生存能力的Logistic回归模型计算,获得了各防空基础指标参数的回归系数β∗,其绝对值可以用来度量防空基础指标参数对重要目标防空威胁指数的影响程度,模型计算结果如表4所示.基础指标参数的回归系数绝对值越大表明它对防空体系指标的影响程度越大.例如x8代表防空体系通信网络的联通数量,它的回归系数β∗8绝对值较大表明通信网络联通数量对防空体系的体系作战能力影响程度较大,它所代表的物理意义与实际信息化条件下防空作战过程是相符的.因此,β∗的绝对值能够反映出各防空基础指标参数对防空体系能力指标的影响程度. 4.4.1 模型验证 在红方防空体系基本案的实验背景上,加载蓝方空袭机群指挥通信协同网络,加强对红方防空体系的攻击强度,获得的部分基础指标仿真数据xj和实验结果y如表5中的验证案.把防空体系验证案的仿真实验数据作为测试集检验以基本案仿真数据作为训练集挖掘出的防空体系指标是否有效,其检验输出值见表5中验证案的Y值,与防空体系验证案的仿真实验结果y一致,验证了所选防空体系威胁指数指标及其度量的一般有效性. 4.4.2 目标预测 根据实验获得的一组基础指标参数值,通过防空体系重要目标威胁指数模型,可以快速预测重要目标被摧毁的概率. 防空体系仿真预测案的实验背景为:在红方防空体系验证案的基础上,加载蓝方电子战飞机,对红方防空体系进行全面电磁干扰,获得的部分基础指标仿真数据xj及防空威胁指数预测结果Y如表5中的预测案.因此,指挥员可以依据威胁指数实时做出决策并调整防空部署. 4.4.3 体系实时监控 防空体系威胁指数运用到实际对抗仿真实验中,可以实时动态显示防空体系中重要目标受到敌空中威胁的程度. 选择预测案2为例,实验过程中,防空体系在第5min发现识别目标,第10min开始发生交战,第30min重要防护目标被摧毁.其防空威胁指数随时间的变化如图4所示:红色圆点为各时刻防空体系重要防护目标的防空威胁指数预测值,蓝色曲线为防空威胁指数的最优拟合曲线,显示重要防护目标的防空威胁指数的变化趋势.其中在15min∼28min之间有一个不确定区间,正是防空体系与敌空袭机群激烈交战阶段,反映了防空体系复杂交互的高度不确定性.部分重要防空基础指标参数的变化率(∆xj/∆t)如图5所示,展示了防空体系作战的前30min内重要防空基础指标参数的变化率情况:其主要变化区间也集中在发生激烈交战的不确定区间内,如第25min显示交战后重要基础指标变化率均为较快负增长,表明敌我态势可能发生了逆转.指挥员可以实时观测体系防空威胁指数的变化和重要基础指标参数变化率的改变情况,决定是否加强防空力量配置或者适时转移重要目标,为指挥员定下作战决心提供决策依据. 表4 归一化后的防空基础指标参数的回归系数绝对值 表5 防空体系对比案仿真实验数据及预测结果 本文基于武器装备体系仿真试验床,构建了“整体、动态、对抗”的防空体系仿真实验,采用随机森林和广义线性回归组合算法模型,对仿真实验获取的“多角度、全维度”对抗数据进行深度挖掘:筛选对防空生存能力显著性基础参数指标,并在此基础上进行二次线性回归,最终构建反映防空体系作战不确定性、自适应性、涌现性等复杂特点的体系能力指标—–防空体系重要目标的防空威胁指数.同时,依据重要基础指标参数对防空威胁指数的聚合涌现关系,进一步分析了重要基础指标对防空威胁指数的贡献度.通过进一步比对实验设计,验证了体系能力指标模型的有效性,预测的准确性和实时监测的可行性.同时,防空威胁指数和重要基础指标参数的动态变化趋势为指挥员实时调整作战方案,并对方案进行评估预测提供了可行的决策依据. 本文初步尝试了运用机器学习方法挖掘防空体系能力指标并对体系能力进行“测量”的方法,今后将进一步优化相关模型算法提高数据挖掘的精度,并针对不同问题挖掘出更多的防空体系能力指标,进而构建出防空体系能力指标网. 图4 重要目标的防空威胁指数实时动态显示图 图5 重要防空基础指标参数的变化率图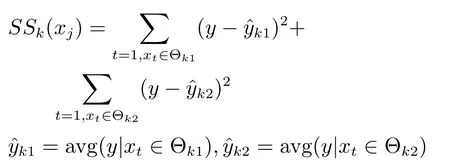
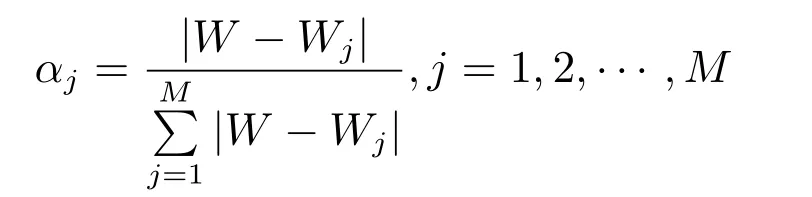

3.2 基于广义线性回归算法的体系指标选取模型
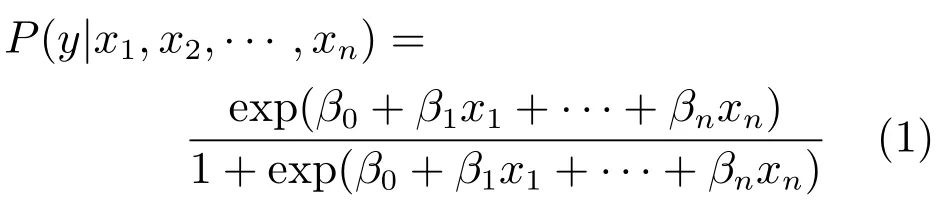
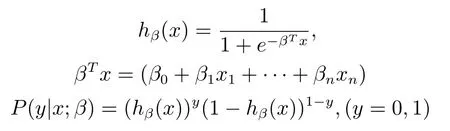
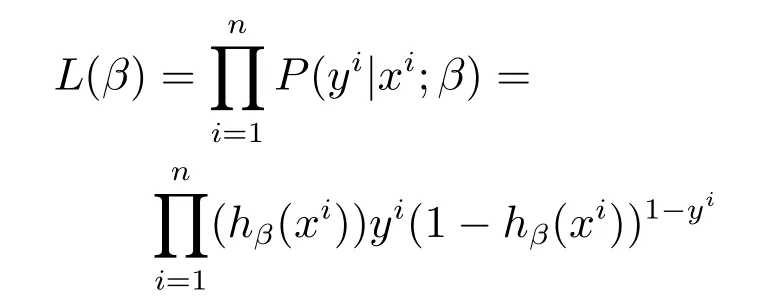
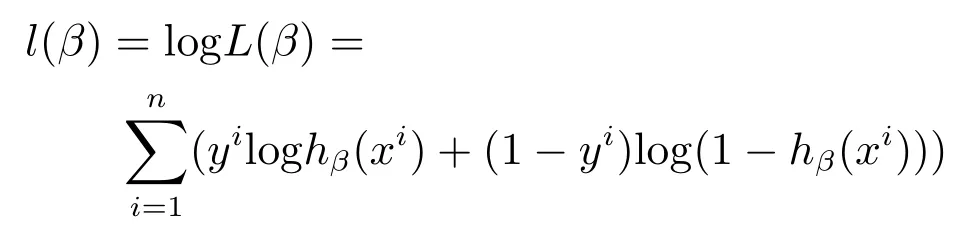
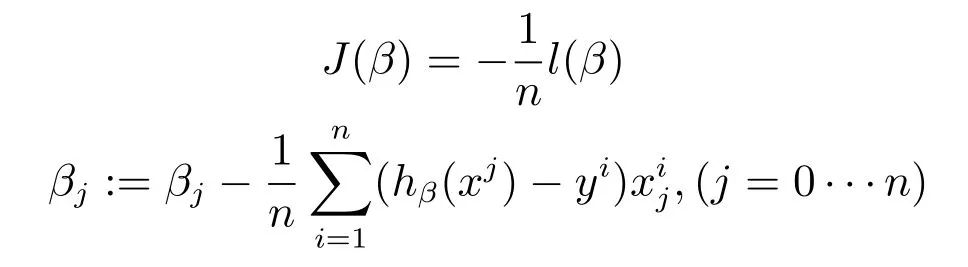
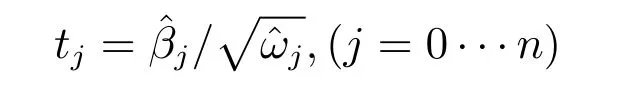
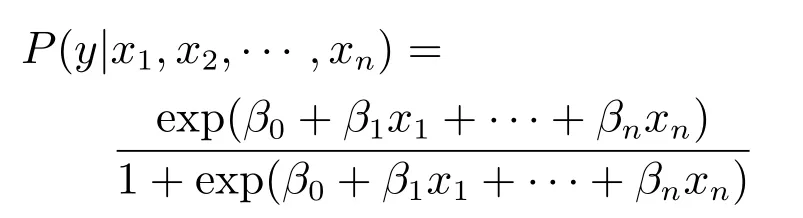
4 防空体系能力指标的选取和验证
4.1 基于随机森林算法的基础指标参数重要性分析
4.2 基于广义线性回归算法的防空体系作战能力指标的挖掘
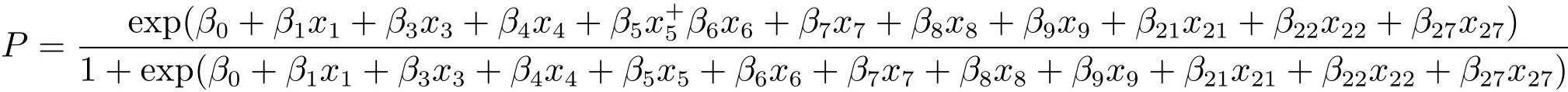
4.3 基础指标参数对防空体系指标的影响度
4.4 体系指标有效性验证和预测

5 结论